Расчет объем окружности: Калькулятор для расчета объема цилиндра

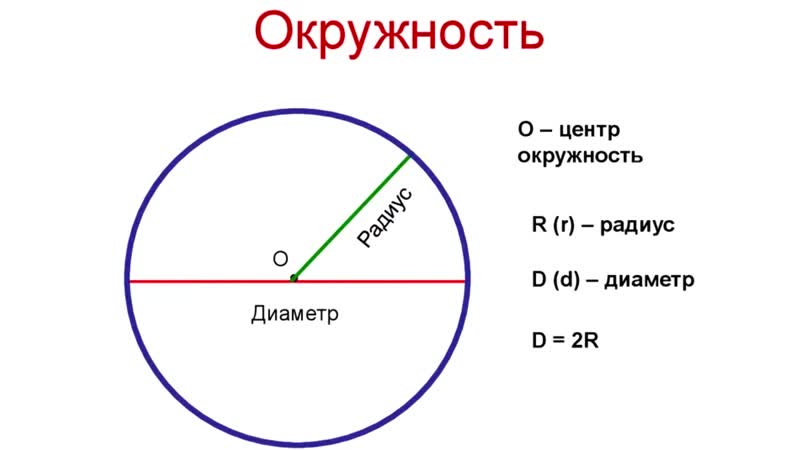
Формула объёма шара

Шар это геометрическое тело, образованное в результате вращения полукруга на оси своего диаметра.

Вычислить объем шара

Формула расчёта объёма шара

 

Объем шара можно вычислить по формуле:

 

 

R – радиус шара

V – объем шара

π – 3.14

Пример нахождения объёма шара

 

Задача:

Найти объем шара радиусом 10 сантиметров.

Решение:

Для того чтобы вычислить объем шара формула используется следующая:

где V – искомый объем шара, π – 3,14, R – радиус.

Таким образом, при радиусе 10 сантиметров объем шара равен:

V

=

4 3

3,14 × 103

= 4186,7

кубических сантиметров.

В геометрии шар определяется как некое тело, представляющее собой совокупность всех точек пространства, которые располагаются от центра на расстоянии, не более заданного, называемого радиусом шара. Поверхность шара именуется сферой, а сам он образуется путем вращения полукруга около его диаметра, остающегося неподвижным.

С этим геометрическим телом очень часто сталкиваются инженеры-конструкторы и архитекторы, которым часто приходится вычислять объем шара. Скажем, в конструкции передней подвески подавляющего большинства современных автомобилей используются так называемые шаровые опоры, в которых, как нетрудно догадаться из самого названия, одними из основных элементов являются именно шары. С их помощью происходит соединение ступиц управляемых колес и рычагов. От того, насколько правильно будет

вычислен их объем, во многом зависит не только долговечность этих узлов и правильность их работы, но и безопасность движения.

В технике широчайшее распространение получили такие детали, как шариковые подшипники, с помощью которых происходит крепление осей в неподвижных частях различных узлов и агрегатов и обеспечивается их вращение. Следует заметить, что при их расчете конструкторам требуется

найти объем шара (а точнее – шаров, помещаемых в обойму) с высокой степенью точности. Что касается изготовления металлических шариков для подшипников, то они производятся из металлической проволоки при помощи сложного технологического процесса, включающего в себя стадии формовки, закалки, грубой шлифовки, чистовой притирки и очистки. Кстати говоря, те шарики, которые входят в конструкцию всех шариковых ручек, изготавливаются по точно такой же технологии.

Достаточно часто шары используются и в архитектуре, причем там они чаще всего являются декоративными элементами зданий и других сооружений. В большинстве случаев они изготавливаются из гранита, что зачастую требует больших затрат ручного труда.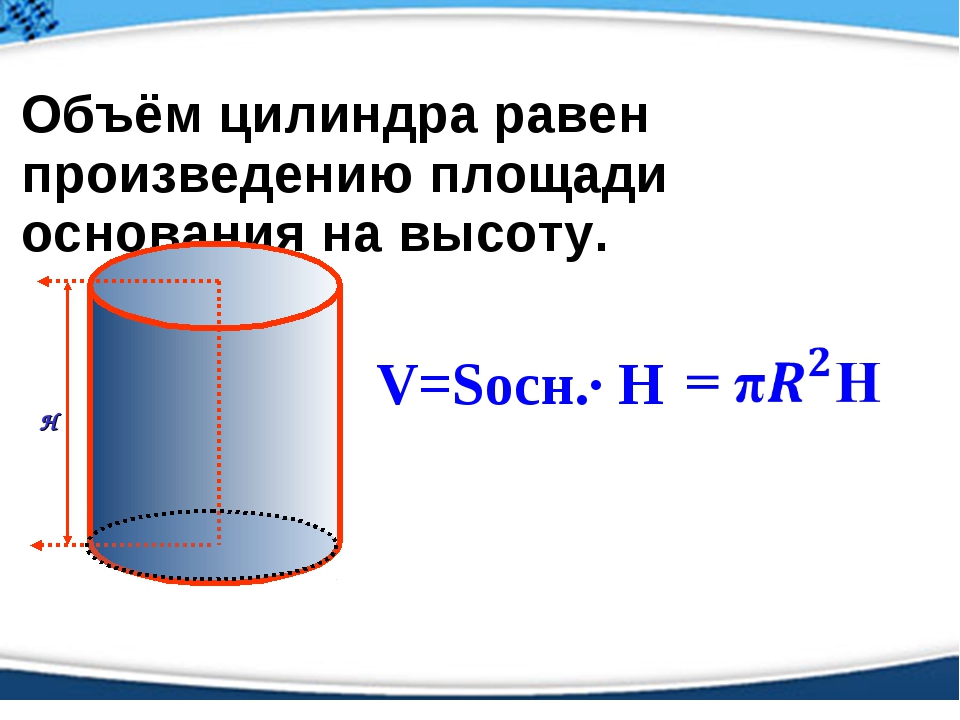

Конечно, соблюдать столь высокую точность изготовления этих шаров, как тех, которые применяются в различных агрегатах и механизмах, не требуется.

Без шаров немыслима такая интересная и популярная игра, как бильярд. Для их производства используются различные материалы (кость, камень, металл, пластмассы) и используются различные технологические процессы. Одним из основных требований, предъявляемых к бильярдным шарам, является их высокая прочность и способность выдерживать высокие механические нагрузки (прежде всего, ударные). Кроме того, их поверхность должна представлять собой точную сферу для того, чтобы обеспечивалось плавное и ровное качение по поверхности бильярдных столов.

Наконец, без таких геометрических тел, как шары, не обходится ни одна новогодняя или рождественская елка. Изготавливаются эти украшения в большинстве случаев из стекла методом выдувания, и при их производстве наибольшее внимание уделяется не точности размеров, а эстетичности изделий.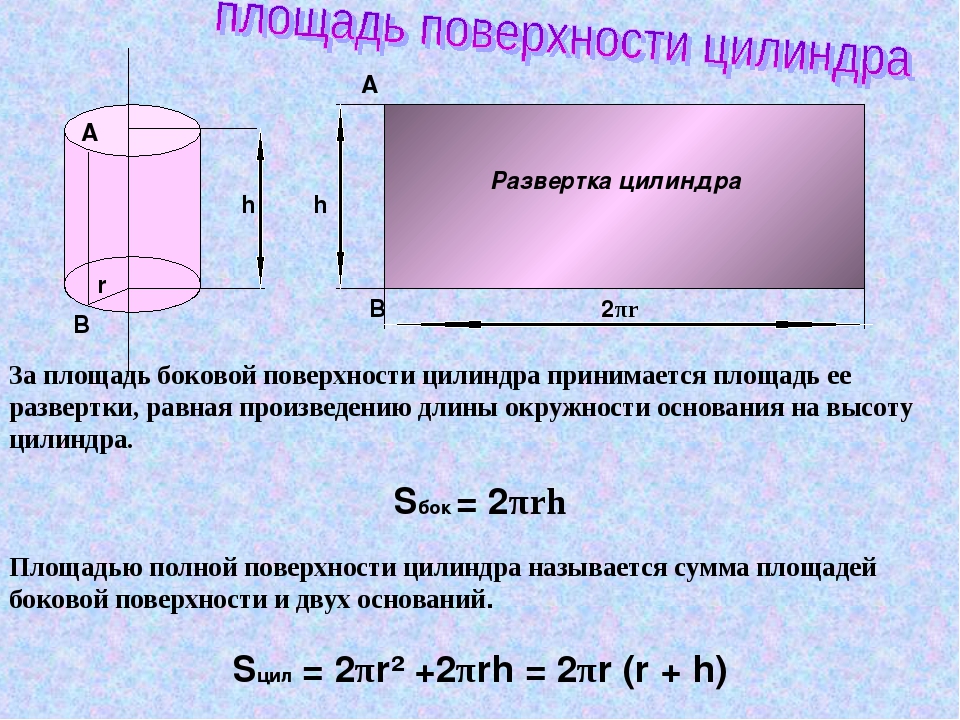 Технологический процесс при этом практически полностью автоматизирован и вручную елочные шары только упаковываются.

Онлайн калькулятор расчета объема бетона

Для точного определения времени выполнения работ по бетонированию и количества расходуемого материала следует провести расчеты, в этом поможет онлайн калькулятор расчета объема бетона.

Калькулятор объема бетона самостоятельно рассчитает для вас необходимое количество раствора, предоставив максимально точные цифры. Расход учитывается в кубических метрах.

Рассчитать объем бетона фундаментной плиты или стяжки

Калькулятор ниже производит расчет бетона на плитный фундамент в соответствии со строительными нормами и правилами. Для расчета плитного фундамента необходимо знать площадь и толщину плиты, т.к. плита – это обыкновенный прямоугольный параллелепипед.

Плитный фундамент представляет собой замкнутую железобетонную цельную монолитную плиту, которая укладывается под всю площадь дома, распределяя тем самым нагрузку по всей длине.

Введите свои данные в поля для расчёта:

Площадь = Длина * Ширина фундаментной плины

Для выполнения расчетов нужно вести длину и ширину помещения (площадь основания), толщину стяжки. Измерить прямоугольник можно по самой опалубке или взять цифры из чертежной документации.

Если количество воды при изготовлении смеси определяете “на глаз”, а песок может быть разного объема и плотности, калькулятор может дать погрешность 10-20 %.

Правильно посчитать кубатуру бетона в этом случае намного сложнее: длину конструкции, в которую входит периметр с внешней стороны и длину всех перегородок между комнатами, мы должны умножить на ее высоту и ширину (при условии, что лента фундамента имеет по всей длине одинаковое сечение).

Обязательно нужно учитывать глубину грунтовых вод, ландшафт, почву и прочие факторы при расчете высоты фундамента.

Столбчатый фундамент считается одним из самых простых в изготовлении и, кроме этого, достаточно экономным по затратам на стройматериалы.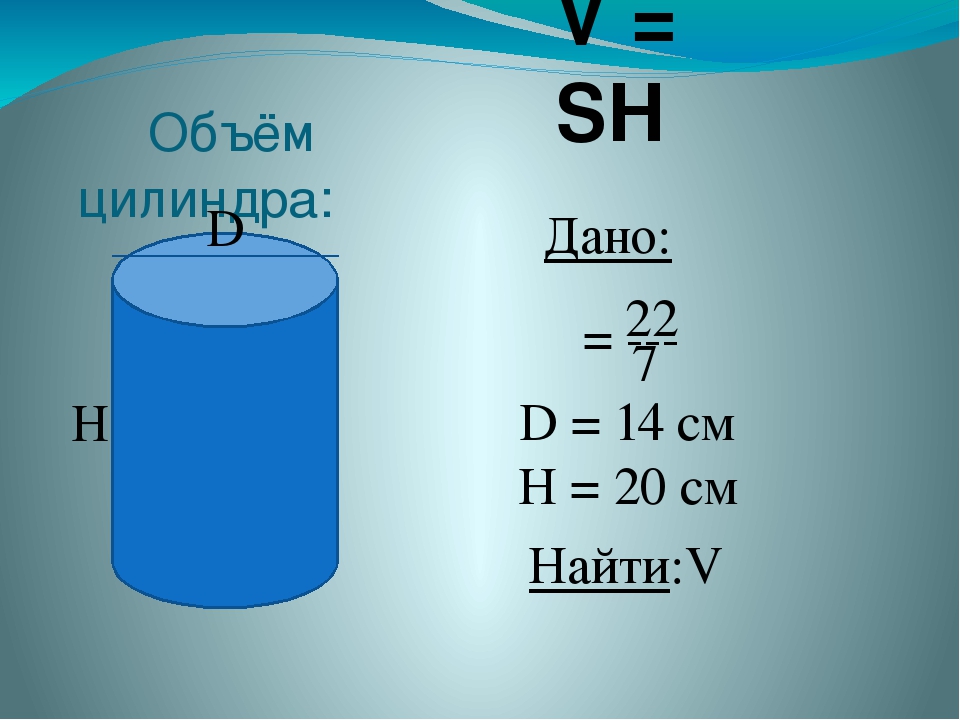

Фундамент состоит из ростверка (верхней части свайного или столбчатого фундамента, распределяющей нагрузку от несущих элементов здания) и свай (вертикальных опорных элементов), поддерживающих горизонтальную часть конструкции над грунтом. Расчет объема бетона здесь сложнее, чем в предыдущих случаях.

Нужно заранее спланировать расход материалов при штукатурных работах, так как неожиданная остановка в работе может сказаться на качестве выполненной работы.

Калькулятор может давать погрешность от 3 до 10% объема из-за не точности производства земляных работ, усадки грунта (бетон тяжелее воды в 2.5 раза), а так же незначительные потери при разгрузке бетона.

Расчёт количества бетона для фундамента разных видов и пола

Отличительной особенностью всех конструкций, создаваемых из бетона, является сложность их геометрической формы. Как же произвести расчёт количества бетона для них? Наиболее распространённым и эффективным способом выполнить эту задачу станет разбивка предполагаемой конструкции на отдельные, более простые составляющие детали.

Благодаря этому расчёт количества бетона для фундамента можно осуществить достаточно быстро.

При проведении математических операций следует учитывать, что наличие элементов арматуры, общая часть которых составляет примерно 5-10% объёма заливки, можно не принимать во внимание и считать погрешностью, потерями монтажа.

Расчёт бетона для столбчатого фундамента

Столбчатый фундамент может создаваться двумя способами:

• сваи погружаются в почву;
• армированный бетон заливается в подготовленные скважины.

Такие конструкции являются достаточно распространёнными, поскольку не требуют большого расхода строительных материалов и достаточно просты в возведении. Столбчатый фундамент подходит для строительства относительно лёгких объектов, которые расположены на грунтах, склонных к вспучиванию или характеризующихся глубоким залеганием несущего слоя.

Рассмотрим, как осуществляется расчёт бетона для фундамента этого вида.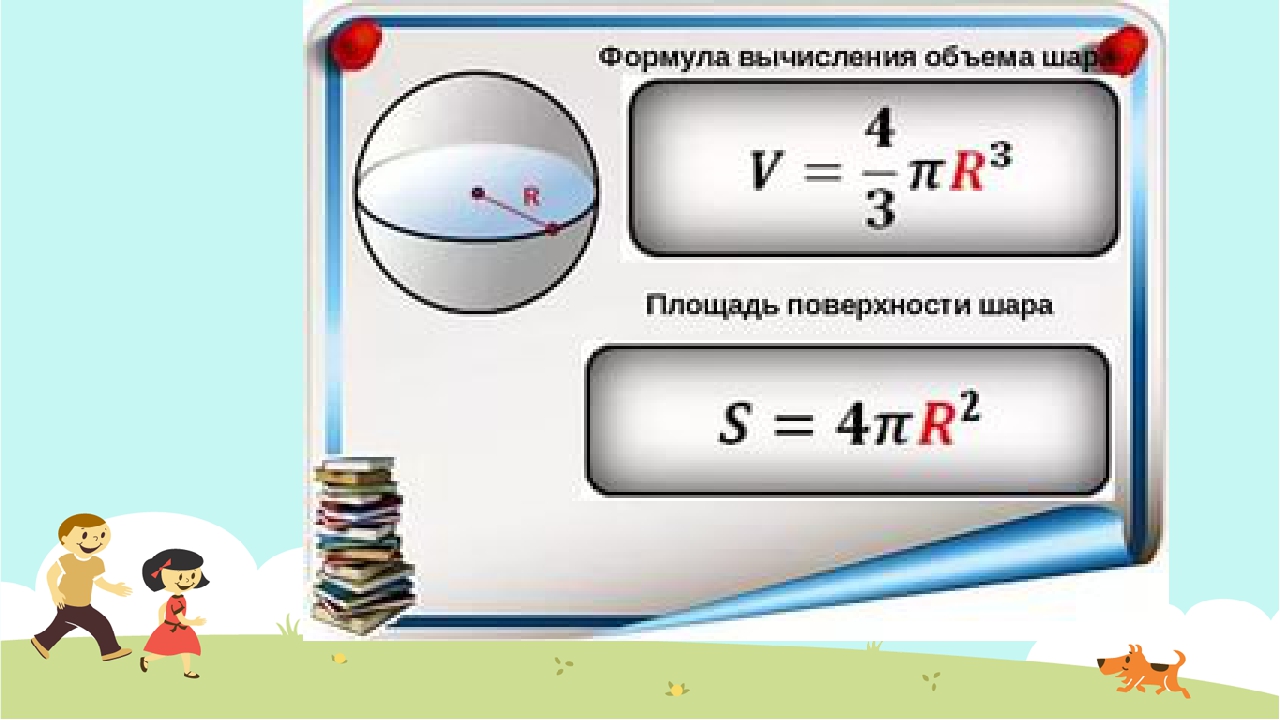 Используем следующую формулу, в которой учитывается площадь поперечного сечения каждого столба:

S = 3.14 х R2, где

R – радиус столбика.

Полученный результат необходимо умножить на высоту элементов конструкции (Н) и их общее число.

Данная формула для расчёта количества бетона может применяться для любых столбиков − независимо от их размера и формы сечения (круг или квадрат).

Расчёт бетона для ленточного фундамента

С необходимостью провести расчёт бетона для фундамента этого типа строители сталкиваются достаточно часто, поскольку конструкция пользуется популярностью.

Основными достоинствами ленточного фундамента являются простота создания и высокие характеристики прочности, что позволяет использовать его при возведении загородных домов и строений малой этажности.

Расчёт объёма ленточного фундамента прост: необходимо получить произведение трёх показателей − высоты, ширины и длины ленты.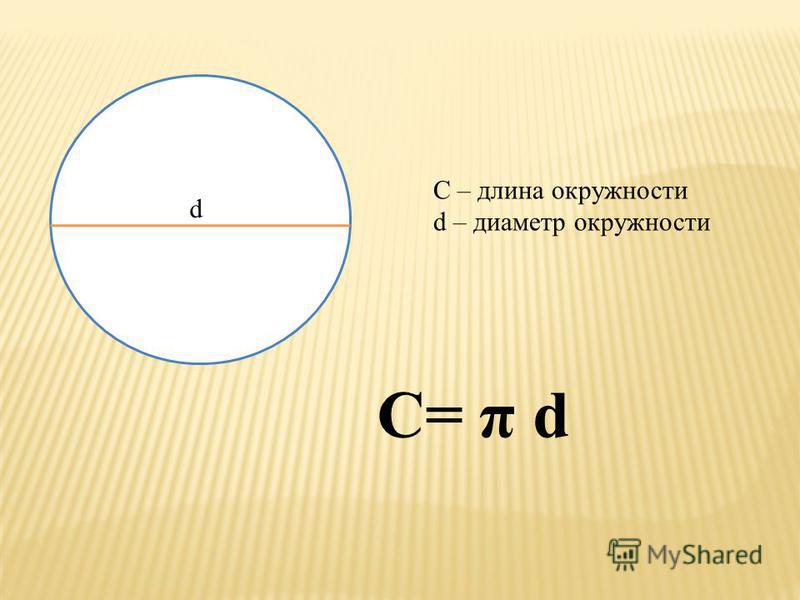

Следует учитывать, что высота фундаментной ленты складывается из двух величин − глубины закладки и части, находящейся над землёй. Сумма этих показателей должна превышать ширину фундамента минимум в два раза. Также нужно понимать, что общая длина ленты − это не только периметр внешних сторон, но и длина всех межкомнатных перегородок. Последние совсем не обязательно являются несущими конструкциями, так что под ними может закладываться более лёгкий фундамент, что нужно учесть при расчёте количества бетона.

Общий объём количества бетона рассчитывается по формуле:

V = S x L, где:

S — площадь поперечного сечения фундаментной ленты (в метрах),

L – общая длина ленты фундамента (в метрах).

Если сечение ленты фундамента разное на различных длинах, то расчёт бетона сложнее: вычисления ведутся для каждого показателя отдельно, а полученные результаты суммируются.

Расчёт бетона для плитного фундамента

Этот вид фундамента является монолитной железобетонной конструкцией, которая размещена под всей площадью постройки. Сферой использования плитного фундамента являются:

• объекты, расположенные на сложных грунтах;
• здания, на которых не предусмотрены подвальные помещения;
• строения, где плиты играют роль основания для пола.

Отличительными особенностями фундамента этого вида является минимальное давление на грунт и высокий показатель жёсткости. Часто при создании плитного фундамента используются рёбра жёсткости, наличие которых необходимо учитывать при расчёте количества бетона.

Объём бетона рассчитывается по такой формуле:

V = S x H, где:

S – площадь плиты;

H – толщина плиты.

Если при возведении фундамента используются рёбра жёсткости, то их объём рассчитывается отдельно и суммируется с показателем объёма плиты.

Расчёт количества бетона для создания пола

Для того чтобы выровнять покрытие и в дальнейшем декорировать его, необходимо сформировать стяжку пола.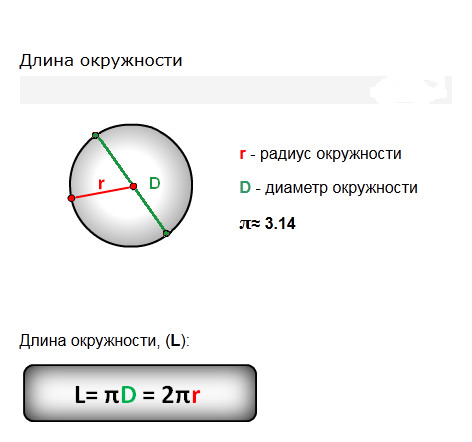 Её толщина колеблется в пределах от 40 до 100 мм и непосредственно зависит от состава бетона и преследуемой цели. Следует учитывать, что недостаточно толстая стяжка склонна к растрескиванию и преждевременному разрушению.

Расчёт количества бетона нужно проводить крайне внимательно, поскольку нехватка материала может крайне негативно сказаться на качестве конструкции, а заливку стяжки нужно производить за один раз, чтобы образовался монолит.

Если формирование стяжки проводится на горизонтальной поверхности, то расчёт количества бетона осуществляется по такой формуле:

V = S x H, где:

S – площадь поверхности стяжки;

H – толщина стяжки.

Гораздо сложнее произвести правильный расчёт количества бетона, если основа не является горизонтальной и, соответственно, стяжка имеет различную толщину на участках базовой поверхности. В этом случае для рабочих процессов и проведения расчётов используются усреднённые величины, так что есть риск нехватки или перерасхода материала.

Объем шара. Объём шарового сегмента,шарового слоя,шарового сектора

Объем шара

Теорема: 

Объём шара радиуса R равен  ⁴/₃ π R³

                                                              

 

Доказательство:

 Рассмотрим шар радиуса R с центром в точке О и выберем ось Ох произвольным образом. Сечение шара плоскостью, перпендикулярной к оси Ох и проходя­щей через точку М этой оси, является кругом с центром в точке М.Обозначим радиус этого круга через r, а его площадь через S(х), где х — абсцисса точки М.Выразим S(х) через х и R. Из прямо­угольного треугольника ОМС находим:

Так как S(x)=πr², то S (x)= π(R^{2 _} x²⁾

Заметим, что эта формула верна для любого положения точки М на диаметре АВ, т.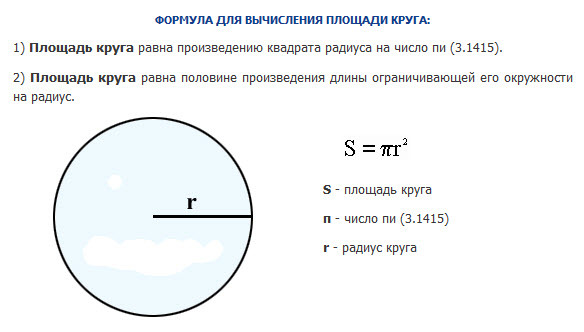 е. Для всех х,удовлетворяющих условию -R ≤ x ≤ R. Применяя основную формулу для вычисления объемов тел при a= — R, b= — R, получим

Теорема доказана.

Шаровой сегмент. Объём шарового сегмента.

Шаровой сегмент – это часть шара, которая осекается плоскостью от шара.

Шаровым сегментом называется часть шара, отсе­ченная от него плоскостью . Всякая плоскость, пересекающая шар, разби­вает его на два сегмента. Объем шарового сегмента находится при помощи тех же рас­суждений из , стоит лишь веять не все тело («цилиндр без конуса»), а его часть, отсеченную плоскостью, параллельной основанию. 

Рассмотрим, например, шаровой сегмент, лежащий выше секущей плоскости, проведенной на высоте х от плоскости основания полушара, т.е. на расстоянии h=R-x от верхней точки полушара.  Искомый объем будет равен раз­ности объемов цилиндра радиуса R с высотой h и усеченного конуса; так как радиус малого основания конуса равен h=R-x, то получаем для                                                                   объема сегмента

                                                                               

 

 Шаровой слой.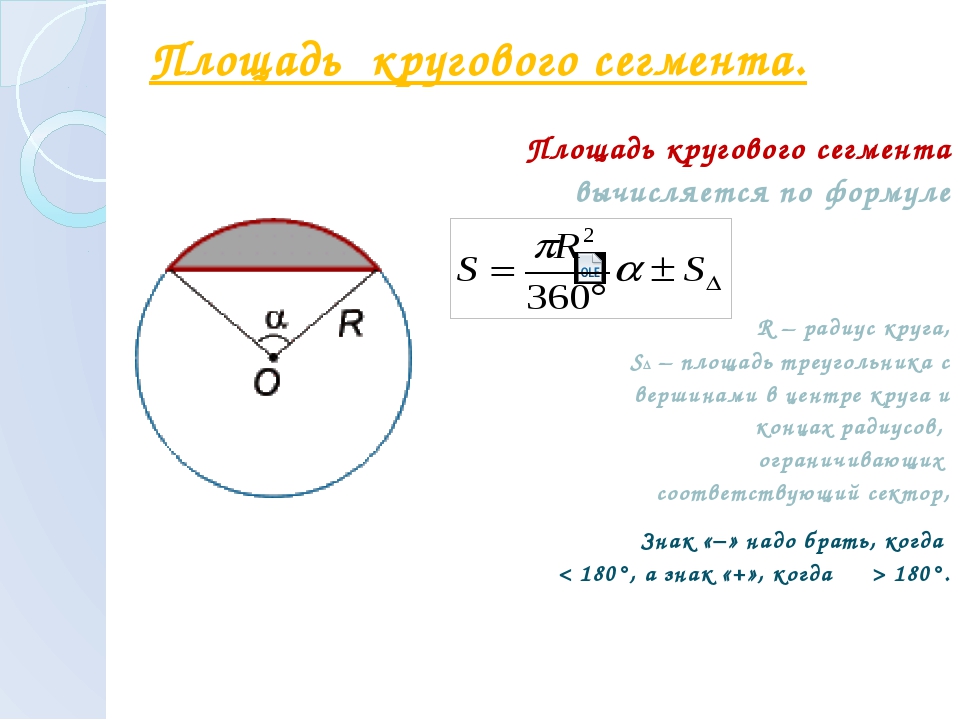 Объём шарового слоя.

Шаровым слоем называется часть шара, заключённая между двумя параллельными секущими плоскостями. Объём шарового слоя можно найти как разность объёмов двух шаровых сегментов, и запоминать отдельную формулу для его вычисления нет надобности.

Шаровой сектор. Объём шарового сектора.

 Шаровой сектор – это часть сферы или шара, которая ограничена кривой поверхностью шарового сегмента и поверхностью конической. Вершиной в данном случае будет служить центр шара, основанием сегмента является та самая коническая поверхность. Чтобы стало более понятно, посмотрите на рисунок.

 Объем шарового сектора можно найти по формуле:  

   

       

       Где h – это высота сегмента, а r— радиус шара.

                                                                                           

Формулы объема геометрических фигур.

Объем геометрической фигуры

— количественная характеристика пространства, занимаемого телом или веществом. Объём тела или вместимость сосуда определяется его формой и линейными размерами.

Объем куба

Объем куба равен кубу длины его грани.

Формула объема куба:

V = a³

где V — объем куба,
a — длина грани куба.

Объем призмы

Объем призмы равен произведению площади основания призмы, на высоту.

Формула объема призмы:

V = S_o h

где V — объем призмы,
S_o — площадь основания призмы,
h — высота призмы.

Объем параллелепипеда

Объем параллелепипеда равен произведению площади основания на высоту.

Формула объема параллелепипеда:

V = S_o · h

где V — объем параллелепипеда,
S_o — площадь основания,
h — длина высоты.

Объем прямоугольного параллелепипеда

Объем прямоугольного параллелепипеда равен произведению его длины, ширины и высоты.

Формула объема прямоугольного параллелепипеда:

V = a · b · h

где V — объем прямоугольного параллелепипеда,
a — длина,
b — ширина,
h — высота.

Объем пирамиды

Объем пирамиды равен трети от произведения площади ее основания на высоту.

Формула объема пирамиды:

где V — объем пирамиды,
S_o — площадь основания пирамиды,
h — длина высоты пирамиды.

Объем правильного тетраэдра

Формула объема правильного тетраэдра:

где V — объем правильного тетраэдра,
a — длина ребра правильного тетраэдра.

Объем цилиндра

Объем цилиндра равен произведению площади его основания на высоту.

Формулы объема цилиндра: где V — объем цилиндра,
S_o — площадь основания цилиндра,
R — радиус цилиндра,
h — высота цилиндра,
π = 3.141592.

Объем конуса

Объем конуса равен трети от произведению площади его основания на высоту.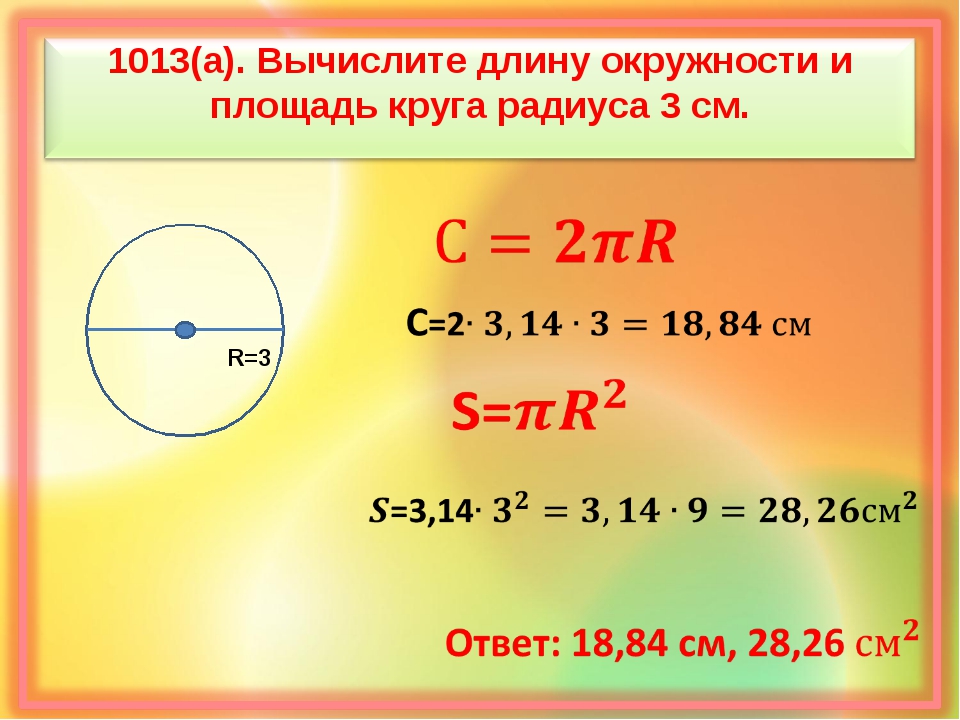

Формулы объема конуса:

где V — объем конуса,
S_o — площадь основания конуса,
R — радиус основания конуса,
h — высота конуса,
π = 3.141592.

Объем шара

Объем шара равен четырем третьим от его радиуса в кубе помноженного на число пи.

Формула объема шара:

где V — объем шара,
R — радиус шара,
π = 3.141592.

Любые нецензурные комментарии будут удалены, а их авторы занесены в черный список!

Вычисление формулы объема и площади в Excel

Программа Excel является лучшим калькулятором. Мы привыкли использовать для расчетов традиционные бухгалтерские калькуляторы. Все их возможности поддерживает программа Excel. Более того, он имеет неоспоримые преимущества.

В некоторых формулах можно выполнить только одно математическое вычисление при калькуляционных расчетах. В таких случаях, если меняются данные нужно изменить формулу. Но если все данные будут распределены по ячейкам, а формула будет только ссылаться на них, то при любых изменениях нет необходимости менять формулу. 3 (A2 – это ссылка на ячейку).

В ячейке A2 будем вводить разные радиусы и после каждого ввода в ячейке B2 будем получать результат вычисления объема сфер соответствующих своим радиусам.

Примечание. Если вы используете в Excel многократные вычисления или формулы содержащие ссылки на ячейки в качестве переменных значений, то всегда подписывайте каждую ячейку с входящими данными и формулами. Это позволит избежать ошибок и легко читать значения или результаты вычисления формул.

формула для определения объема бревна

При покупке необработанного леса каждый кубический дециметр для нас очень важен. Особенно если мы точно рассчитали количество необходимого леса для последующего распила либо оцилиндрованных бревен. Поэтому очень важно знать точный объем поставляемого леса-кругляка.

Обмер и учет лесных материалов.

Так как пиломатериалы и поставляемый вес при расчетах учитывают в кубических метрах, то стоимость леса измеряется в денежных единицах за кубический м.

Поэтому нужно знать фактический объем древесины, которую вы заказываете или покупаете.

Этот объем, выраженный в кубических метрах, и будет кубатурой леса.

Произведение расчета кубатуры леса по кубатурнику

Пример расчет кубатуры бревна с помощью он-лаин программы.

Наиболее распространенным методом определения объема круглого бревна является использование кубатурника. Это специальная таблица расчета кубатуры. Кубатурник позволяет по длине бревна с шагом 0,5 метра и диаметру хлыста (более тонкой части бревна) определить объем данного бревна в кубических метрах с точностью до тысячных. Для этого измеряются диаметр вершины бревна и длина бревна и по ним проводят расчет кубатуры в кубатурнике. Если сечение бревна на срезе хлыста недостаточно круглое, тогда измеряется самый большой диаметр и самый малый при перпендикулярных измерениях. Из них вычисляется среднее, округляют его до ближайшего целого, по которому и ищут в кубатурнике объем бревна. Кубатурник регламентирован ГОСТ 2708-75 , ISO 4480-83 ”Лесоматериалы круглые. Таблицы объемов”.

При необходимости вычисления объема древесины в складометрах нужно вычислить объем каждого бревна и их сложить.

Если длина бревна намного больше, чем есть в кубатурнике, то вычисление кубатуры бревна производят путем сложения кубатуры двух его составляющих.

Однако этот метод вычисления довольно неточен и может привести к большой переплате за поставленный лес.

Поэтому приходится искать более точные методы вычисления объема круглого леса.

Вернуться к оглавлению

Расчет кубатуры оцилиндрованного бревна

Расчет кубатуры оцилиндрованного бревна и профилированного бруса.

Если бревна оцилиндрованные, то точный объем этого бревна можно рассчитать по формуле вычисления объема цилиндра:

V = π_*D²_*L/4, где

• V – кубатура бревна, м³;
• D – диаметр бревна, м;
• L – длина бревна, м;
• π – постоянная.

Но мы стремимся узнать более точный объем необработанного круглого леса, бревна которого имеют сбежистость.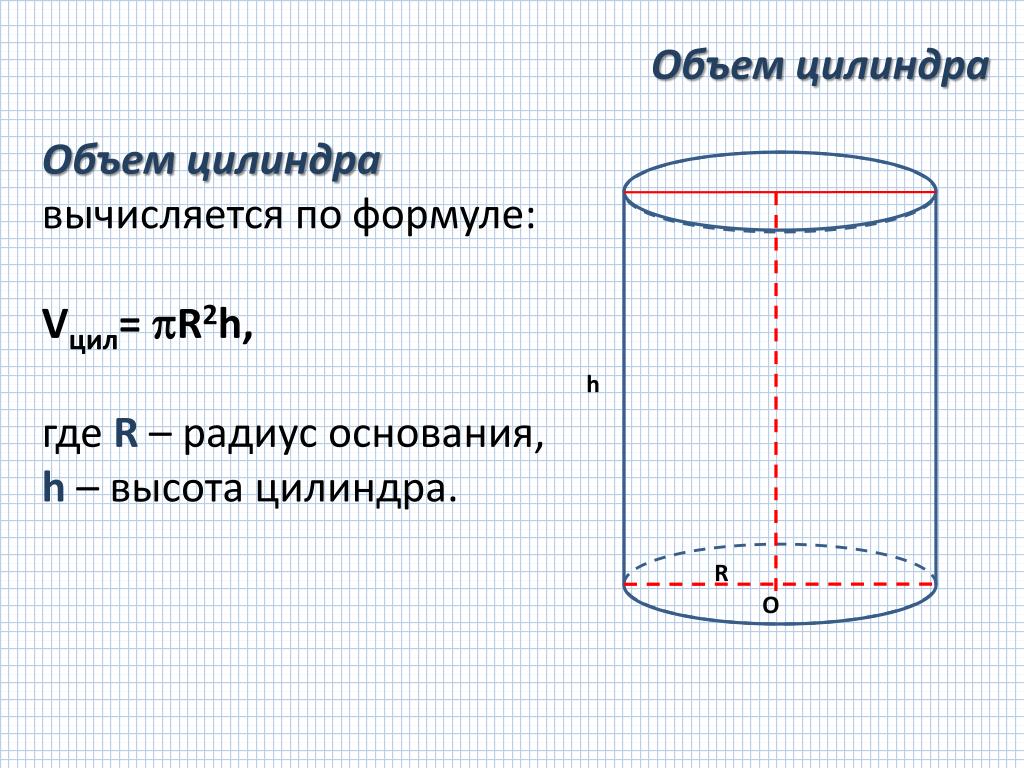

Сбежистостью называют изменение диаметра круглых бревен лесоматериалов от одного конца к другому. Она измеряется в % и вычисляется делением разницы диаметров на длину, на которой эта разница обнаруживается. Нормальный сбег (сбежистость) равен 1% (1 см на 1 м длины бревна). Сбежистость увеличивает количество отходов при их распиловке и оцилиндрении бревен.

Вернуться к оглавлению

Формула расчета кубатуры леса

Таблица расчета кубатуры бревен.

В стандартном кубатурнике предусматривается некоторая сбежистость, и поэтому все данные в нем вычислены по диаметру хлыстов вершины.

Но сбежистость у разных деревьев бывают разная. Нормальная сбежистость принимается только для хвойных деревьев, и то лишь при укрупненных расчетах. Для насаждений ІІ и ІІІ бонитетов среднее значение сбежистости в промежутке диаметров бревна от 14 до 60 см колеблется от 0,8% до 1,8%.

Поэтому предлагается следующий способ более точного определения фактического объема бревна необработанного леса. Для начала измеряется диаметр бревна на вершине и его длина, а затем измеряется диаметр комля одного из наиболее характерных по сбегу бревен. На следующем этапе вычисляется сбежистость бревен – разница диаметров комля и хлыста делится на длину бревна. Например, если бревно длиной 8 м имеет диаметр на вершине в двух перпендикулярных направлениях 14 и 16 см, а диаметр среза в комлевой части 22 и 24 см, то сбежистость бревна вычисляем по формуле:

С=(D1+D2-d1- d2) / 2L, где

• d1,d2 – диаметр бревна на верхнем срезе (хлысте) соответственно по двум перпендикулярным направлениям, см;
• D1,D2 – диаметр бревна на нижнем срезе (комле) соответственно по двум перпендикулярным направлениям, см;
• L – длина бревна, м.

В нашем случае С = (22+24-16-14) см²_* 8 м=1,0 см/м.

То есть для данной древесины на одном метре длины ствола его диаметр уменьшается от комля до хлыста на 1,0 см (нормальная).

При правильной окружности срезов, когда d1=d2 и D1=D2; С=(D-d) /L

Зная длину бревна и диаметр одного конца (нижнего или верхнего) по формуле вычисления, которая выведена из геометрической формулы объема усеченного конуса, определяем объем любого бревна:

V =π _* (D²+D_*d + d²) _*L/120000, где

• d =(d1+d2)/2 – диаметр бревна на верхнем срезе (хлысте), вычисленный по его размерам соответственно по двум перпендикулярным направлениям, см;
• D =d+С_*L – диаметр бревна на нижнем срезе (комле), вычисленный исходя из диаметра бревна на верхнем срезе (хлысте) и его сбежалости, см;
• L – длина бревна, м;
• С – сбежалость, см/м.

В приведенном выше случае V = 3,14_* (23²+ 23_* 15+15²)_* 8/12000=0,23 м³ , хотя таблица расчета по кубатурнику дает объем 0,199 м³. Результат очевиден.

Поэтому, если лес покупать, лучше измерять по ГОСТу, а если продавать, то по приведенной формуле.

Объем цилиндров — объяснение и примеры

Объем цилиндра — это мера пространства, занимаемого цилиндром, или мера вместимости цилиндра.

Эта статья покажет вам, как найти объем цилиндра с помощью формулы объема цилиндра.

В геометрии цилиндр представляет собой трехмерную форму с двумя равными и параллельными окружностями, соединенными изогнутой поверхностью.

Расстояние между круговыми гранями цилиндра называется высотой цилиндра .Верх и низ цилиндра представляют собой две совпадающие окружности, радиус или диаметр которых обозначены как « r » и « d » соответственно.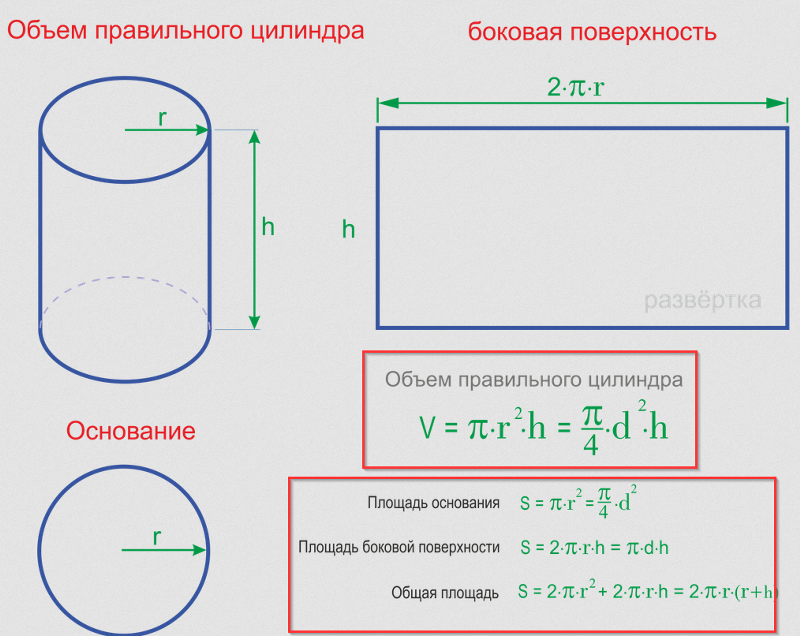

Как найти объем цилиндра?

Чтобы вычислить объем цилиндра, вам понадобится радиус или диаметр круглого основания или вершины и высота цилиндра.

Объем цилиндра равен произведению площади круглого основания и высоты цилиндра. Объем цилиндра измеряется в кубических единицах.

Расчет объема цилиндра полезен при проектировании цилиндрических объектов, таких как:

• Цилиндрические резервуары для воды или колодцы
• Кульверты
• Флаконы для духов или химикатов
• Цилиндрические контейнеры и трубы
• Цилиндрические колбы, используемые в химические лаборатории

Формула объема цилиндра

Формула для объема цилиндра имеет следующий вид:

Объем цилиндра = πr ² ч кубических единиц

Где πr ² = площадь круга ;

π = 3.14;

r = радиус круглого основания и;

h = высота цилиндра.

Для полого цилиндра формула объема имеет следующий вид:

Объем цилиндра = πh (r ₁ ² — r ₂ ² )

Где, r ₁ = внешний радиус и r ₂ = внутренний радиус цилиндра.

Разница внешнего и внутреннего радиуса образует толщину стенки цилиндра, т.е.

Толщина стенки цилиндра = r ₁ — r ₂

Давайте решим несколько примеров задач об объеме цилиндров.

Пример 1

Диаметр и высота цилиндра составляют 28 см и 10 см соответственно. Какой объем цилиндра?

Решение

Дано;

Радиус равен половине диаметра.

Диаметр = 28 см ⇒ радиус = 28/2

= 14 см

Высота = 10 см

По формуле объема цилиндра;

объем = πr ² ч

= 3,14 x 14 x 14 x 10

= 6154.4 см ³

Итак, объем цилиндра 6154,4 см ³

Пример 2

Глубина воды в цилиндрическом резервуаре составляет 8 футов. Предположим, что радиус и высота резервуара составляют 5 футов и 11,5 футов соответственно. Найдите объем воды, необходимый для наполнения бака до краев.

Раствор

Сначала рассчитайте объем цилиндрического резервуара

Объем = 3,14 x 5 x 5 x 11,5

= 902.75 кубических футов

Объем воды в резервуаре = 3,14 x 5 x 5 x 8

= 628 кубических футов.

Объем воды, необходимый для заполнения бака = 902,75 — 628 кубических футов

= 274,75 кубических футов.

Пример 3

Объем цилиндра 440 м ³ , радиус основания 2 м. Рассчитайте высоту резервуара.

Раствор

Объем цилиндра = πr ² ч

440 м ³ = 3.14 x 2 x 2 x h

440 = 12,56h

Разделив 12,56 на обе стороны, получим

h = 35

Таким образом, высота резервуара будет 35 метров.

Пример 4

Радиус и высота цилиндрического резервуара для воды составляют 10 см и 14 см соответственно. Найдите объем бака в литрах.

Раствор

Объем цилиндра = πr ² ч

= 3,14 x 10 x 10 x 14

= 4396 см ³

Дано, 1 литр = 1000 кубических сантиметров (см ³ )

Следовательно, разделите 4396 на 1000, чтобы получить

Объем = 4.396 литров

Пример 5

Внешний радиус пластиковой трубы составляет 240 мм, а внутренний радиус — 200 мм. Если длина трубы составляет 100 мм, найдите объем материала, из которого изготовлена ​​труба.

Решение

Труба является примером полого цилиндра, поэтому мы имеем

Объем цилиндра = πh (r ₁ ² — r ₂ ² )

= 3,14 x 100 x (240 ² -200 ² )

= 3.14 x 100 x 17600

= 5,5264 x 10 ⁶ мм ³ .

Пример 6

Цилиндрический твердый блок металла должен быть расплавлен с образованием кубов с ребром 20 мм. Предположим, что радиус и длина цилиндрического блока равны 100 мм и 490 мм соответственно. Найдите количество кубиков, которые нужно сформировать.

Решение

Рассчитайте объем цилиндрического блока

объем = 3,14 x 100 x 100 x 490

= 1.5386 x 10 ⁷ мм ³

Объем куба = 20 x 20 x 20

= 8000 мм ³

Количество кубиков = объем цилиндрического блока / объем куба

= 1,5386 x 10 ⁷ мм ³ /8000 мм ³

= 1923 куба.

Пример 7

Найдите радиус цилиндра такой же высоты и объема, как у куба со сторонами 4 фута

Решение

Дано:

Высота куба = высота цилиндра = 4 футов и,

объем куба = объем цилиндра

4 x 4 x 4 = 64 кубических фута

Но объем цилиндра = πr ² ч

3.14 x r ² x 4 = 64 кубических фута

12,56r ² = 64

Разделите обе стороны на 12,56

r ² = 5,1 футов.

r = 1,72

Следовательно, радиус цилиндра будет 1,72 фута.

Пример 8

Сплошная шестиугольная призма имеет длину основания 5 см и высоту 12 см. Найдите высоту цилиндра того же объема, что и призма. Примем радиус цилиндра 5 см.

Раствор

Формула объема призмы имеет вид;

Объем призмы = (h) (n) (s ² ) / [4 tan (180 / n)]

где n = количество сторон

s = базовая длина призмы

h = высота призмы

Объем = (12) (6) (5 ² ) / (4tan 180/6)

= 1800/2.3094

= 779,42 см ³

Объем цилиндра = πr ² h

779,42 = 3,14 x 5 x 5 x h

h = 9,93 см.

Итак, высота цилиндра будет 9,93 см.

Практические вопросы

1. Если объем и радиус цилиндрической коробки для краски составляют 640π кубических см и 8 см соответственно, какова его высота?
2. Рассмотрим цилиндрический резервуар, высота которого в два раза больше его радиуса. Если объем резервуара составляет 4580 единиц, каков радиус резервуара?

Ответы

1. 10 см
2. 9 единиц

Предыдущий урок | Главная страница | Следующий урок

Объем частично заполненного цилиндра с калькулятором

Объем частично заполненного цилиндра с калькулятором — Math Open Reference

Определение: форма, образованная при разрезании цилиндра плоскостью, параллельной сторонам цилиндра.

Попробуй это Перетащите оранжевые точки, обратите внимание, как меняется громкость.

Если мы возьмем горизонтальный цилиндр и разрежем его на две части, используя надрез, параллельный сторонам цилиндра, мы получим два горизонтальных сегмента цилиндра. На рисунке выше нижний показан синим цветом. Другой — прозрачная часть сверху.

Если мы посмотрим на конец цилиндра, мы увидим, что это круг, разрезанный на два сегмента круга. Подробнее см. Определение сегмента круга.

Всякий раз, когда у нас есть твердое тело, поперечное сечение которого одинаково по длине, мы всегда можем найти его объем, умножив площадь конца на его длину. Таким образом, в этом случае объем сегмента цилиндра равен площади сегмента круга, умноженной на длину.

Итак, формула объем горизонтального цилиндрического сегмента равен Где
s = площадь сегмента круга, образующего конец твердого тела, а
l = длина цилиндра.

Площадь сегмента круга может быть найдена по его высоте и радиусу круга.
См. Площадь сегмента круга с учетом высоты и радиуса.

Калькулятор

Используйте калькулятор ниже, чтобы рассчитать объем горизонтального сегмента цилиндра. Он был настроен для практического случая, когда вы пытаетесь найти объем жидкости в цилиндрическом резервуаре. путем измерения глубины жидкости.

Для удобства он преобразует объем в жидкие единицы, такие как галлоны и литры, если вы выберете нужные единицы.Если вы не укажете единицы измерения, объем будет в тех единицах, которые вы использовали для ввода размеров. Например, если вы использовали футов, тогда объем будет в кубических футах. Используйте одинаковые единицы для всех трех входов.

Как формула

объем = где:
R — радиус цилиндра.
D — это глубина.
L — длина цилиндра Примечания :

• Результат функции cos ^-1 в формуле выражен в радианах.
• В формуле используется радиус цилиндра. Это половина его диаметра.
• Все входы должны быть в одних и тех же единицах. Результат будет в этих кубических единицах. Так, например, если входные данные указаны в дюймах, результат будет в кубических дюймах. При необходимости результат должен быть преобразован в единицы объема жидкости, такие как галлоны.

Связанные темы

(C) Открытый справочник по математике, 2011 г.
Все права защищены.

математических формул для основных фигур и трехмерных фигур

В математике (особенно в геометрии) и естественных науках вам часто нужно вычислять площадь поверхности, объем или периметр различных форм.Будь то сфера или круг, прямоугольник или куб, пирамида или треугольник, каждая форма имеет определенные формулы, которым вы должны следовать, чтобы получить правильные измерения.

Мы собираемся изучить формулы, которые понадобятся вам для определения площади поверхности и объема трехмерных фигур, а также площади и периметра двухмерных фигур. Вы можете изучить этот урок, чтобы изучить каждую формулу, а затем сохранить ее для быстрого ознакомления в следующий раз, когда она вам понадобится. Хорошая новость заключается в том, что в каждой формуле используются одни и те же базовые измерения, поэтому изучение каждого нового становится немного проще.

Площадь и объем сферы

Д. Рассел

Трехмерный круг известен как сфера. Чтобы рассчитать площадь поверхности или объем сферы, вам необходимо знать радиус ( r ). Радиус — это расстояние от центра сферы до края, и оно всегда одинаково, независимо от того, от каких точек на краю сферы вы измеряете.

Когда у вас есть радиус, формулы довольно просто запомнить. Как и в случае с окружностью круга, вам нужно будет использовать число пи ( π ).Как правило, это бесконечное число можно округлить до 3,14 или 3,14159 (принятая дробь — 22/7).

• Площадь поверхности = 4πr ²
• Объем = 4/3 πr ³

Площадь поверхности и объем конуса

Д. Рассел

Конус — это пирамида с круглым основанием, имеющая наклонные стороны, которые сходятся в центральной точке. Чтобы рассчитать его площадь поверхности или объем, необходимо знать радиус основания и длину стороны.

Если вы этого не знаете, вы можете найти длину стороны ( s ), используя радиус ( r ) и высоту конуса ( h ).

После этого вы можете найти общую площадь поверхности, которая является суммой площади основания и площади стороны.

• Площадь базы: πr ²
• Площадь стороны: πrs
• Общая площадь поверхности = πr ² + πrs

Чтобы найти объем сферы, вам нужны только радиус и высота.

Площадь и объем цилиндра

Д. Рассел

Вы обнаружите, что с цилиндром намного легче работать, чем с конусом. Эта форма имеет круглое основание и прямые параллельные стороны. Это означает, что для определения его площади поверхности или объема вам понадобятся только радиус ( r ) и высота ( h ).

Тем не менее, вы также должны учитывать то, что есть как верх, так и низ, поэтому радиус необходимо умножить на два для площади поверхности.

• Площадь поверхности = 2πr ² + 2πrh
• Объем = πr ² ч

Площадь и объем прямоугольной призмы

Д. Рассел

Прямоугольник в трех измерениях становится прямоугольной призмой (или коробкой). Когда все стороны равны, он становится кубом. В любом случае для определения площади поверхности и объема требуются одни и те же формулы.

Для этого вам нужно знать длину ( х ), высоту ( х ) и ширину ( х ).С кубом все три будут одинаковыми.

• Площадь поверхности = 2 (левый) + 2 (левый) + 2 (белый)
• Объем = л / ш

Площадь и объем пирамиды

Д. Рассел

С пирамидой с квадратным основанием и гранями из равносторонних треугольников работать сравнительно легко.

Вам нужно будет знать размер одной длины основания ( b ). Высота ( х ) — это расстояние от основания до центральной точки пирамиды.Сторона ( s ) — это длина одной грани пирамиды от основания до верхней точки.

• Площадь поверхности = 2bs + b ²
• Объем = 1/3 б ² ч

Другой способ вычислить это — использовать периметр ( P ) и площадь ( A ) базовой формы. Это можно использовать для пирамиды с прямоугольным, а не квадратным основанием.

• Площадь поверхности = (½ x P x s) + A
• Объем = 1/3 Ач

Площадь поверхности и объем призмы

Д.Рассел

При переходе от пирамиды к равнобедренной треугольной призме необходимо также учитывать длину ( l ) формы. Запомните сокращения для основания ( b ), высоты ( h ) и стороны ( s ), потому что они необходимы для этих вычислений.

• Площадь поверхности = bh + 2ls + lb
• Объем = 1/2 (бч) л

Тем не менее, призма может быть любой формы. Если вам нужно определить площадь или объем нечетной призмы, вы можете полагаться на площадь ( A ) и периметр ( P ) базовой формы.Часто в этой формуле будет использоваться высота призмы или глубина ( d ), а не длина ( l ), хотя вы можете видеть любое сокращение.

• Площадь поверхности = 2A + Pd
• Объем = объявления

Площадь сектора круга

Д. Рассел

Площадь сектора круга может быть вычислена в градусах (или радианах, как это чаще всего используется в расчетах). Для этого вам понадобятся радиус ( r ), пи ( π ) и центральный угол ( θ ).

• Площадь = θ / 2 r ² (в радианах)
• Площадь = θ / 360 πr ² (в градусах)

Площадь эллипса

Д. Рассел

Эллипс также называют овалом и по сути представляет собой удлиненный круг. Расстояния от центральной точки до стороны непостоянны, что делает формулу для определения ее площади немного сложной.

Чтобы использовать эту формулу, вы должны знать:

• Semiminor Axis ( a ): кратчайшее расстояние между центральной точкой и краем.
• Большая полуось ( b ): наибольшее расстояние между центральной точкой и краем.

Сумма этих двух точек остается постоянной. Вот почему мы можем использовать следующую формулу для вычисления площади любого эллипса.

Иногда вы можете увидеть эту формулу, записанную как r ₁ (радиус 1 или малая полуось) и r ₂ (радиус 2 или большая полуось), а не a и b .

Площадь и периметр треугольника

Треугольник — одна из самых простых фигур, и вычислить периметр этой трехсторонней формы довольно просто. Вам необходимо знать длины всех трех сторон ( a, b, c ), чтобы измерить полный периметр.

Чтобы узнать площадь треугольника, вам понадобится только длина основания ( b ) и высота ( h ), которая измеряется от основания до вершины треугольника. Эта формула работает для любого треугольника, независимо от того, равны ли стороны или нет.

Площадь и окружность круга

Подобно сфере, вам нужно знать радиус ( r ) круга, чтобы узнать его диаметр ( d ) и длину окружности ( c ). Имейте в виду, что круг — это эллипс, у которого одинаковое расстояние от центральной точки до каждой стороны (радиуса), поэтому не имеет значения, где на краю вы измеряете.

• Диаметр (d) = 2r
• Окружность (c) = πd или 2πr

Эти два измерения используются в формуле для вычисления площади круга.Также важно помнить, что отношение длины окружности к ее диаметру равно пи ( π ).

Площадь и периметр параллелограмма

У параллелограмма есть два набора противоположных сторон, идущих параллельно друг другу. Форма четырехугольная, поэтому у нее четыре стороны: две стороны одной длины ( a ) и две стороны другой длины ( b ).

Чтобы узнать периметр любого параллелограмма, используйте эту простую формулу:

Когда вам нужно найти площадь параллелограмма, вам понадобится высота ( х ).Это расстояние между двумя параллельными сторонами. Также требуется основание ( b ), это длина одной из сторон.

Имейте в виду, что b в формуле площади не то же самое, что b в формуле периметра. Вы можете использовать любую из сторон, которые были соединены как a и b при вычислении периметра, хотя чаще всего мы используем сторону, перпендикулярную высоте.

Площадь и периметр прямоугольника

Прямоугольник — это тоже четырехугольник.В отличие от параллелограмма, внутренние углы всегда равны 90 градусам. Кроме того, стороны, противоположные друг другу, всегда будут иметь одинаковую длину.

Чтобы использовать формулы для периметра и площади, вам необходимо измерить длину прямоугольника ( l ) и его ширину ( w ).

• Периметр = 2h + 2w
• Площадь = в x ш

Площадь и периметр квадрата

Квадрат даже проще, чем прямоугольник, потому что это прямоугольник с четырьмя равными сторонами.Это означает, что вам нужно знать только длину одной стороны ( с ), чтобы найти ее периметр и площадь.

Площадь и периметр трапеции

Трапеция — это четырехугольник, который может показаться сложной задачей, но на самом деле это довольно просто. У этой формы только две стороны параллельны друг другу, хотя все четыре стороны могут иметь разную длину. Это означает, что вам нужно знать длину каждой стороны ( a, b ₁ , b ₂ , c ), чтобы найти периметр трапеции.

• Периметр = a + b ₁ + b ₂ + c

Чтобы найти площадь трапеции, вам также понадобится высота ( х ). Это расстояние между двумя параллельными сторонами.

Площадь и периметр шестиугольника

Шестигранный многоугольник с равными сторонами — это правильный шестиугольник. Длина каждой стороны равна радиусу ( r ). Хотя это может показаться сложной формой, вычисление периметра — это простой вопрос умножения радиуса на шесть сторон.

Определить площадь шестиугольника немного сложнее, и вам придется запомнить эту формулу:

Площадь и периметр восьмиугольника

Правильный восьмиугольник похож на шестиугольник, но у этого многоугольника восемь равных сторон. Чтобы найти периметр и площадь этой формы, вам понадобится длина одной стороны ( a ).

• Периметр = 8a
• Площадь = (2 + 2√2) a ²

Калькулятор кругов

Что такое площадь и периметр круга?

Набор точек на плоскости, одинаково удаленных от заданной точки $ O $, представляет собой окружность.Точка $ O $ называется центром окружности. Расстояние от центра круга до любой точки на окружности называется радиусом этого круга. Радиус круга должен быть положительным вещественным числом. Окружность с центром $ O $ и радиусом $ r $ обозначается $ c (O, r) $.
Расстояние вокруг круга называется периметром или окружностью круга. Обычно обозначается как $ C $.

Если все вершины многоугольника принадлежат окружности, то многоугольник называется вписанным. Если все стороны многоугольника касаются окружности, то многоугольник называется описанным.

Метод определения длины окружности: Впишем в круг правильный многоугольник, например квадрат. Затем удвойте количество сторон этого многоугольника, чтобы получить восьмиугольник. Если продолжить процесс удвоения количества сторон правильные вписанные многоугольники, мы получаем бесконечную последовательность периметров правильных многоугольников, которая увеличивается. Эта возрастающая последовательность ограничена, поскольку периметры всех вписанных выпуклых многоугольников меньше периметра любого описанного многоугольника.Итак, эта возрастающая последовательность периметров имеет определенный предел. Этот предел — окружность. Следовательно, окружность круга — это предел периметра правильного многоугольника, вписанного в круг, когда число его вершин бесконечно удваивается. Поскольку все круги похожи, отношение длины окружности к диаметру одинаковое для всех кругов. Это отношение длины окружности к диаметру обозначается греческой буквой $ \ pi \ приблизительно 3,14 $. Таким образом, формула для окружности

$$ C = D \ times \ pi $$

или же

$$ C = 2 \ times r \ times \ pi $$

Архимед [Хит, Т.L., it A History of Greek Mathematics, 2 vol., Oxford, 1921] дал приближение к $ \ pi $ с помощью $$ \ pi \ приблизительно \ frac {22} 7 = 3,142857142857 … $$
Метод определения площади круга: Площадь круга — это количество квадратных единиц внутри этого круга. Разделив круг на равные части, как показано на рисунке ниже, мы можем переставить части примерно в прямоугольник. Длина этот приблизительный прямоугольник равен половине окружности круга, $ r \ times \ pi $. Ширина этого примерного прямоугольника равна радиусу окружности $ r $.2) $ и т. Д.

Работа с площадью и периметром круга с шагом показывает полное пошаговое вычисление для нахождения окружности и площади круга с радиусом длиной $ 8 \; in $ с использованием формул окружности и площади. . Для любое другое значение длины радиуса круга, просто введите положительное действительное число и нажмите кнопку СОЗДАТЬ РАБОТУ. Учащиеся начальной школы могут использовать этот круговой калькулятор для создания работы, проверки результатов периметра и площади двумерных фигур или для эффективного выполнения домашних заданий.2} \ times h \]

\ [198 = (28,274 …) \ times h \]

\ [h = 198 \ div (28,274 …) \]

\ [h = 7,002 .. . \]

\ (h = 7см \) (с точностью до см)

Формула площади и объема для геометрических фигур

пи (π) = 3,1415926535 …

+ высота основания

8 csc (theta1) + csc (theta2)] полукруглый (1/4) × n × сторона ² × кроватка (pi / n) вс сторона стороны) 3) × пи × радиус ³ 9097 1

Формула периметра
Квадрат	4 × сторона
Прямоугольник	2 × (длина + ширина)
Параллелограмм	2 × 6 9097 9097 9097	стороны		сторона1 + сторона2 + сторона3
Правильный n-образный многоугольник	n × сторона
Трапеция	высота × (основание1 + основание2) / 2
Трапеция
Круг	2 × pi × радиус
Эллипс	4 × radius1 × E (k, pi / 2) E (k, pi / 2) — полный эллиптический интеграл второго рода k = (1 / radius1) × sqrt (radius1 2 — radius2 2 )
Формула площади
Квадрат	сторона 2
Прямоугольник	длина × ширина
Параллелограмм	основание × высота
Треугольник	основание × высота / 2
полукруглый
Трапеция	высота × (base1 + base2) / 2
Круг	pi × радиус 2
Эллипс	пи × радиус1 × радиус2
Куб (поверхность)	6 × сторона 2
Сфера (поверхность)	4 × пи × радиус 2
периметр окружности × высота
	2 × pi × радиус × высота
Цилиндр (вся поверхность)	Площади верхней и нижней окружностей + Площадь стороны
	2 (пи × радиус 2 ) + 2 × пи × радиус × высота
Конус (поверхность)	пи × радиус × сторона
Тор (поверхность)	pi 2 × (радиус2 2 — радиус1 2 )
Формула объема
Куб	сторона 3
Прямоугольная призма	сторона1	сторона 2 × сторона3
Эллипсоид	(4/3) × пи × радиус1 × радиус2 × радиус3
Цилиндр	пи × радиус 2 × высота
Конус	(1/3) × pi × радиус 2 × высота
Пирамида	(1/3) × (площадь основания) × высота
Torus	(1/4) × pi 2 × (r1 + r2) × (r1 — r2) 2

Источник: Spiegel, Murray R.Математический справочник формул и таблиц.
Серия набросков Шаума по математике. McGraw-Hill Book Co., 1968.

Быстрые способы оценки круглых бетонных форм

Когда дело доходит до оценки количества бетона, большинство ремонтников полагаются на предложение субподрядчика. Но иногда бывает проще самостоятельно оценить затраты на небольшую работу, такую ​​как плита патио или группа бетонных опор для поддержки настила. Оба этих примера включают расчет необходимого объема бетона, что достаточно просто для прямоугольной плиты, но немного сложнее для цилиндрической трубы или полукруглой террасы.

В наши дни вы можете ввести несколько цифр в онлайн-калькулятор, который покажет необходимое количество бетона. Но математика, лежащая в основе расчета, проста, и вам не помешает напомнить, как произвести расчет вручную, на случай, если ваш Wi-Fi мигает. Кроме того, я только что обнаружил классный ярлык, который стоит знать.

Объем цилиндра: #TheHardWay

Форма трубы — это высокий тонкий цилиндр, а круглая плита — это короткий широкий цилиндр.Как и для всех цилиндров, для вычисления объема (V) необходимо умножить площадь круга (πr ² ) на высоту (h). Давайте сначала посмотрим на 10-дюймовую трубку высотой 6 футов. Чтобы найти объем, необходимо: 1) найти радиус; 2) конвертировать дюймы в футы; и 3) подставьте результаты в формулу V = πr ² x h [1] .

Ярлык

Хорошо, это было весело, но гораздо проще обратиться к таблице стандартных диаметров труб и количества бетона, необходимого для их заполнения на фут высоты [2] .

Тем не менее, фактическая математика пригодится, когда цилиндр представляет собой плиту для террасы. И это немного проще благодаря ярлыку, который я обнаружил во время просмотра видео на нашем дочернем веб-сайте ProTradeCraft.com, на котором изображен Тим Оделл из Odell Complete Concrete, подрядчика по бетону, обслуживающего округ Ориндж, Калифорния,

Из множества обучающих видеороликов, доступных на веб-сайте компании и на канале YouTube, этот посвящен расчету количества бетона, необходимого для изогнутой плиты внутреннего дворика.В нем Оделл раскрывает ярлык, которого я никогда раньше не видел: площадь круга составляет 78,5% площади квадрата того же размера. Давайте посмотрим на пример.

Оделл ссылается на рисунки террасной плиты в форме пирога, выступающей на 18 футов над домом. Плита представляет собой идеальную четверть круга, и, используя свой ярлык, он находит площадь, беря квадрат того же размера, а затем умножая его на 0,785, чтобы найти площадь круговой формы [3] . Все, что осталось для получения объема, — это умножить на толщину плиты, которая в данном случае составляет 4 дюйма.Чтобы на самом деле заказать бетон, вы, конечно, должны перевести его в кубические ярды.

Сокращение трубки

Этот маленький трюк, так сказать, завершающий круг, работает и с бетонными трубчатыми формами. Возвращаясь к предыдущему примеру трубы диаметром 10 дюймов, площадь 10-дюймового квадрата составляет 100 квадратных дюймов (10 x 10) или 0,69 квадратных футов (100/144). Умножьте это на 0,785, и вы получите 0,545 квадратных футов для площади 10-дюймового круга, образованного трубкой.