Расчитаем площадь поверхности трубы онлайн калькулятором
На чтение 5 мин. Просмотров 2.1k. Обновлено
Защита металла от коррозии является наиболее актуальной задачей при эксплуатации трубопроводов, поэтому очень важно знать площадь, которая нуждается в покрытии изолирующими материалами.
Площадь поверхности трубы рассчитывается онлайн калькулятором с использованием стандартных алгоритмов.
С помощью онлайн калькулятора Вы без труда сможете рассчитать площадь поверхности круглой трубы. Так же предлагаем приемы и формулы, чтобы произвести расчет самостоятельно, без использования калькулятора.
Введите данные в онлайн калькулятор
Трубопроводный транспорт на сегодняшний день является самым эффективным из всех существующих средств доставки жидких сред до потребителя. Само по себе устройство таких транспортных магистралей по себестоимости обходится заметно дешевле автомобильных дорог и железнодорожных магистралей.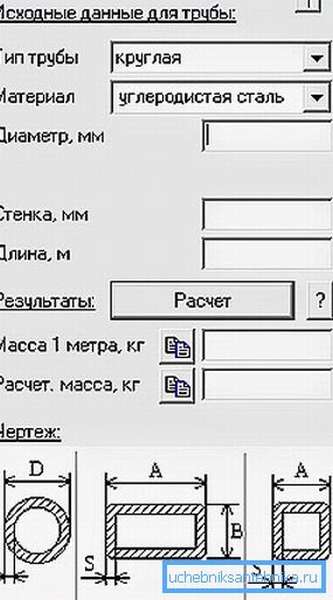 А объемы перекачки на порядок выше, чем при перевозке другими видами транспорта. Для повышения срока службы магистральных трубопроводов производится изоляция наружной, а часто и внутренней поверхностей с различными целями:
А объемы перекачки на порядок выше, чем при перевозке другими видами транспорта. Для повышения срока службы магистральных трубопроводов производится изоляция наружной, а часто и внутренней поверхностей с различными целями:
- Утепление – применяется для предотвращения потерь тепла на магистрали и предотвращения промерзания трубопровода.
- Защита от коррозии с целью продления долговечности трубной магистрали.
- Защита внутренней поверхности – применяется для улучшения проходимости перекачиваемого продукта за счет улучшения качества поверхности, а также для ее защиты при транспортировке химически активных сред.
Чтобы добиться достижения всех этих целей требуется расчет площади поверхности трубы онлайн калькулятором, чтобы оптимально использовать изоляционные материалы. Знать объем поставки необходимо, поскольку логистика при производстве полевых работ занимает значительную часть себестоимости объекта.
Что нужно для подсчета площади поверхности трубы онлайн
Труба представляет собой изделие цилиндрической формы с отсутствующей сердцевиной, по которой и производится транспортировка жидких или газообразных продуктов. Но сейчас нас интересуют плоскости итого изделия, подлежащие обработке изолирующего материала. Перед тем, как посчитать калькулятором площадь трубы в м2, рассмотрим какие исходные данные для этого нужны. Для этого воспользуемся формулой:
Но сейчас нас интересуют плоскости итого изделия, подлежащие обработке изолирующего материала. Перед тем, как посчитать калькулятором площадь трубы в м2, рассмотрим какие исходные данные для этого нужны. Для этого воспользуемся формулой:
S = πd * L, где
S – площадь поверхности, м2;
d – диаметр трубы на поперечном сечении, м;
L – длина, м.
Для примера рассмотрим расчет площади магистральной трубы внешним диаметром 820х10 мм длиной 11,2 метра. Воспользуемся приведенным соотношением, подставив цифровые значения: 3,14 * 0,82 * 0,82 * 11,0 = 23,2 метра квадратных.
Расчетная площадь укрываемой плоскости составит 23,2 м2. Обращаем внимание, что длина трубопровода учтена при размере меньшем, чем фактический размер изделия. Этот связано с тем, что по концам оставляются незакрытые полоски, поскольку на этих местах производится сварка стыка в магистрали. Нанесение изоляции производится после окончания устройства соединения. Предполагается, что основной изолирующий слой выполняется в производственных условиях нанесением полимерно битумного состава и трех слоев пленки из сшитого полиэтилена.
Обращаем внимание, что длина трубопровода учтена при размере меньшем, чем фактический размер изделия. Этот связано с тем, что по концам оставляются незакрытые полоски, поскольку на этих местах производится сварка стыка в магистрали. Нанесение изоляции производится после окончания устройства соединения. Предполагается, что основной изолирующий слой выполняется в производственных условиях нанесением полимерно битумного состава и трех слоев пленки из сшитого полиэтилена.
При определенных условиях изоляция производится при монтаже с применением специального оборудования. Здесь понятно, что очевидна важность расчета площади, чтобы точно рассчитать необходимое количество материалов для доставки к месту монтажа. Не менее важно иметь эти данные, если в качестве изоляции применяется окраска трубопровода специальными составами. Для приведенного случая производится изоляция только наружной плоскости, внутренняя изоляция наносится только в заводских условиях по специальному заказу.
Однако, далеко не всегда нужно заниматься расчетами такого рода. Многие строители используют специальные таблицы для определения площади трубопровода. В них приведенные данные всех размеров по ГОСТ 10704-80 и некоторых других организационно-распорядительных документах, включая и технические условия. Размерный ряд выполняется в соответствии с требованиями указанного стандарта, а это главный показатель для выполнения указанных расчетов.
Многие строители используют специальные таблицы для определения площади трубопровода. В них приведенные данные всех размеров по ГОСТ 10704-80 и некоторых других организационно-распорядительных документах, включая и технические условия. Размерный ряд выполняется в соответствии с требованиями указанного стандарта, а это главный показатель для выполнения указанных расчетов.
Но наиболее употребимыми для получения необходимого результата являются специально разработанные онлайн калькуляторы. Введя исходные данные можно сразу же получить искомый результат.
Расчёт величины наружной поверхности
Он нужен для определения количества лакокрасочных материалов, которое нужно затратить, чтобы нанести слой защитного покрытия. Основой для расчёта являются исходные данные о размерах изделия. Рассчитать величину поверхности цилиндра очень просто с использованием стандартных приёмов из геометрии.
Математической соотношение выглядит следующим образом:
S = 2ПrL, где
- S – величина наружной поверхности трубы;
- r – радиус;
- Пr – число, равное 3,14;
- L – длина окрашиваемого участка.
Таким образом, мы получаем величину наружной поверхности, которая подлежит защитному покрытию. Далее используется норма расхода лакокрасочного материала на единицу площади и поставленную задачу можно считать выполненной.
Но часто возникает необходимость в нанесении защитного покрытия и на внутреннюю плоскость трубы. Это делается для трубопроводов и емкостей, по которым производится транспортировка химически активных жидкостей и газов. Средством защиты в данном случае может быть эмалевое покрытие.
Транспортируемые пищевые продукты защищаются покрытиями из алюминия или цинковыми. Естественно, что для точного понимания о количестве средств защиты нужны параметры величины поверхности.
Внутренняя рассчитывается так же, как наружная, только показатель радиуса берётся по внутреннему размеру, а не по наружному.
Наиболее важными и материалоёмкими примерами изоляции трубопроводов являются нефтепроводы и газопроводы.
Они часто протягиваются по траншеям и их изоляция должна быть сверх надёжной, чтобы обеспечить номинальный срок службы. Она выполняется путём изоляции труб слоем битумного состава с добавлением искусственного каучука, поверх которого наматывается защитная оболочка из крафт – бумаги. Процесс производится в потоке при укладке уже сваренных ниток в траншею.
Она выполняется путём изоляции труб слоем битумного состава с добавлением искусственного каучука, поверх которого наматывается защитная оболочка из крафт – бумаги. Процесс производится в потоке при укладке уже сваренных ниток в траншею.
Такая защита исправно служит не менее 10 лет, причём при весьма значительных давления в трубопроводе. Затем данная магистраль подлежит замене в принудительном порядке. Нужно сказать, что старые трубы извлекаются из земли и поступают на вторичный рынок для использования в строительстве, мелиорации и других областях.
Следует отметить, что необходимость в таких расчётах постоянно снижается. Это происходит по причине роста доли пластиковых труб в трубопроводах низкого давления и самотёчных канализационных, а они не нуждаются в защите, следовательно, и в расчётах такого рода.
Тем не менее, они все ещё необходимы и на сегодняшний день уже никто не пользуется обычным калькулятором, предпочитая использовать сервис интернета для расчёта площади трубопровода онлайн, более точные и оперативные.
Для чего рассчитывают площадь поверхности круглой трубы
Прокладка путепроводов обходится дешевле, чем строительство автомобильных и железных дорог. Перекачка топлива происходит с помощью компрессорных станций на тысячи километров от месторождения к потребителю. Объемы доставляемого сырья по путепроводам на порядок выше, чем при перевозке другими типами транспорта.
Для повышения эффективности работы магистральные и распределительные подземные сети изолируются и утепляются, для этого проводится расчет площади профиля. Изоляция металлических труб необходима для защиты от:
- блуждающих токов;
- разрушающей коррозии;
- теплопотерь (в системах отопления).
Расчет сечения профильной (прямоугольной) трубы на онлайн-калькуляторе
Расчет поможет сэкономить на арматуре, изоляции. Правила логистики учитывают потери при выполнении полевых работ, которые увеличивают себестоимость труда.
Труба — это цилиндрическая пустотелая конструкция большой длины одинакового диаметра на всем ее протяжении.
- S = π d L, где:
- S – площадь поверхности;
- d – диаметр трубы;
- L – длина.
Например, при наружном диаметре 1420 мм и длине 12 м, площадь поверхности круглого проката составляет 53,5 кв. м. На обоих концах изделия оставляется свободное место для сварочного стыка. Слой изоляции накладывается после проведения сварочных работ, испытания конструкции на прочность, герметичность.
Площадь и объем поверхности квадратного или прямоугольного профиля
Размеры вычисляются, исходя из суммы площадей всех сторон. Кроме изолирующих материалов (битума, полимерной пленки), нужно знать объемы жидких красящих веществ, которыми покрывается металлоконструкция. Площадь общей поверхности цилиндрической металлоконструкции:
- S=2π(R+r)(R-r- L), где:
- R — внешний радиус;
- r — внутренний радиус;
- L — длина трубы.

- Площадь наружной поверхности:
- Калькулятор объема круглой трубы:
При проведении расчетов пользуются специальными таблицами.
калькулятор онлайн, расчет, как посчитать
Опубликовано:
28.11.2013
В наше время объединение стран в одно мировое сообщество значительно усиливает взаимозависимость экономики разных стран друг от друга. Это ведет к глобальному перемещению во времени и в пространстве людей, услуг, товаров, сырья. Отсюда и значительное повышение роли транспорта в разных его формах и видах.
Одним из узкоспециализированных видов транспортировки являются трубопроводы, преимущества которых бесспорны и очевидны.
Одним из узкоспециализированных видов транспорта являются трубопроводы, преимущества которых бесспорны и очевидны. Например, если посчитать пропускную способность, то стоимость трубопровода в два с лишним раза меньше железной или автомобильной дороги.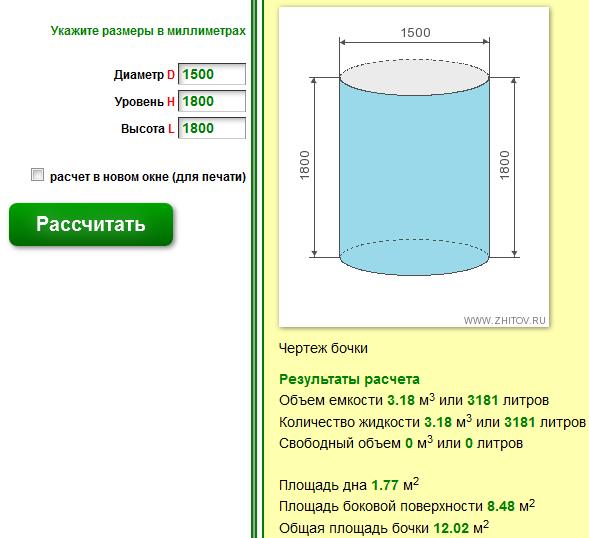
Характеристики трубопроводов
Правильный расчет характеристик трубопроводов поможет вам сэкономить и получить максимум возможностей при проведении как магистрального, так и обычного водопроводного или теплового трубопровода.
На чем же можно сэкономить или получить максимум возможностей, если грамотно рассчитать трубу, как магистральную, так и обычную домашнюю, водопроводную или тепловую? Знание таких выигрышных возможностей и их использование – формула успеха! Остановимся на них поподробнее:
- Проходимость трубопровода – этот показатель влияет и на расход транспортируемого материала, и на стоимость самого сооружения.

- Потери тепла – важный параметр трубопровода при транспортировке теплоносителя (воды) от теплового пункта к отопительным приборам. В формулу расчета теплопотерь, наряду со многими физическими величинами, входит диаметр и длина трубы.
- Количество теплоизолирующего материала – требуется точный расчет площади поверхности трубопровода для максимальной экономии материала и средств.
- Антикоррозийное покрытие трубопровода – правильный расчет покрываемой площади ведет к экономии краски или битумного лака.
- Шероховатость внутренней поверхности – показатель, влияющий на скорость потока в трубе. Чем ниже шероховатость, тем меньше сопротивление стенок трубопровода и выше скорость потока. Переменный показатель, зависящий и от геометрических размеров трубы, и от процесса зарастания ее поперечного просвета ржавчиной и минеральными отложениями.

Площадь внешней поверхности трубы
Поверхность цилиндра – это прямоугольник, одна сторона которого является длиной окружности цилиндра, а вторая сторона есть длина самого цилиндра. А чтобы узнать площадь прямоугольника, надо рассчитать произведение двух его сторон (т.е. произведение длины на ширину).
Задача сугубо геометрическая. Площадь поверхности снаружи есть не что иное, как площадь поверхности цилиндра. А поверхность цилиндра – это прямоугольник, одна сторона которого является длиной окружности цилиндра, а вторая сторона есть длина самого цилиндра. А чтобы узнать площадь прямоугольника, надо рассчитать произведение двух его сторон (т.е. произведение длины на ширину).
Длина окружности равна Pi*D, где Pi – число “пи”, а D – диаметр трубы.
Итого: площадь прямоугольника будет равна: S=Pi*D*L, где Pi – число “пи”, D и L- диаметр и длина трубы.
Приведем пример. Пусть дана теплотрасса диаметром (D) в 1 м и длиной (L) в 10 000 м (10 км), тогда формула площади покраски будет записываться: S=3,14*1*10000=31400 м
 Для теплоизоляции понадобится материал большей площади, так как обычно трубы заворачиваются в минеральную вату с перехлестом полотен.
Для теплоизоляции понадобится материал большей площади, так как обычно трубы заворачиваются в минеральную вату с перехлестом полотен.Площадь внутренней поверхности
Во всех примерах расчета площади брались трубы круглого сечения. Это объясняется тем, что круглая труба имеет наибольший внутренний объем при наименьшей площади поверхности.
Рассчитывается как и площадь внешней поверхности S, где в качестве диаметра D берется величина D-2*N (N – толщина стенки трубы). Формула запишется так: S=Pi*(D-2*N)*L.
Присутствие редких сечений вызвано в основном технологическими и гидравлическими строительными требованиями.
 Основные сферы применения – очистные сооружения канализации и открытые дождевые сети.
Основные сферы применения – очистные сооружения канализации и открытые дождевые сети.Для полноты обзора отметим, что во многих других сферах, особенно строительной, в качестве каркаса изделия находит широкое применение форма профильной трубы (квадратной и прямоугольной). Плоские грани таких труб упрощают монтаж, а их высокая сопротивляемость деформации делают конструкцию прочной и долговечной. Вот почему профиль квадратный или прямоугольный стал достойной альтернативой металлическому швеллеру, балке и уголку. Расчет такой профильной трубы производится аналогично круглой, но с учетом формул площади для квадратного или прямоугольного сечения.
Ну, и совсем уж экзотические формы сечения трубы – это трапецеидальная, пятиугольная, лотковая, полукруглая. Присутствие таких редких сечений вызвано в основном технологическими и гидравлическими строительными требованиями. Основные сферы применения – очистные сооружения канализации и открытые дождевые сети. Чтобы посчитать площадь сечения и поверхности таких труб, необходимо разбить сложный профиль на простые фигуры (круг, треугольник, квадрат, прямоугольник) и работать с ними по известным формулам.

В последнее время, в связи с ростом востребованности расчета трубопроводов и интенсивного проникновения интернет-технологий во все сферы жизни человека, появилось большое количество онлайн-программ и онлайн-инструментов для полного анализа трубопроводных сетей с учетом материала, доставляемого продукта, климатических условий и других сопутствующих параметров. Рассчитать сеть для поперечного сечения круглой, квадратной, прямоугольной и иной формы такие программы могут быстро, точно и, что самое главное, с различными вариациями и указанием диапазона действия величин, которые использует формула.
площади поверхности, толщины стенки, массы
При строительстве и обустройстве дома трубы не всегда используются для транспортировки жидкостей или газов. Часто они выступают как строительный материал — для создания каркаса различных построек, опор для навесов и т.д. При определении параметров систем и сооружений необходимо высчитать разные характеристики ее составляющих.
 В данном случае сам процесс называют расчет трубы, а включает он в себя как измерения, так и вычисления.
В данном случае сам процесс называют расчет трубы, а включает он в себя как измерения, так и вычисления. Содержание статьи
Для чего нужны расчеты параметров труб
В современном строительстве используются не только стальные или оцинкованные трубы. Выбор уже довольно широк — ПВХ, полиэтилен (ПНД и ПВД), полипропилен, металлопластк, гофрированная нержавейка. Они хороши тем, что имеют не такую большую массу, как стальные аналоги. Тем не менее, при транспортировке полимерных изделий в больших объемах знать их массу желательно — чтобы понять, какая машина нужна. Вес металлических труб еще важнее — доставку считают по тоннажу. Так что этот параметр желательно контролировать.
То, что нельзя измерить, можно рассчитатьЗнать площадь наружной поверхности трубы надо для закупки краски и теплоизоляционных материалов. Красят только стальные изделия, ведь они подвержены коррозии в отличие от полимерных. Вот и приходится защищать поверхность от воздействия агрессивных сред.
 Используют их чаще для строительства заборов, каркасов для хозпостроек (гаражей, сараев, беседок, бытовок), так что условия эксплуатации — тяжелы, защита необходима, потому все каркасы требуют окраски. Вот тут и потребуется площадь окрашиваемой поверхности — наружная площадь трубы.
Используют их чаще для строительства заборов, каркасов для хозпостроек (гаражей, сараев, беседок, бытовок), так что условия эксплуатации — тяжелы, защита необходима, потому все каркасы требуют окраски. Вот тут и потребуется площадь окрашиваемой поверхности — наружная площадь трубы.При сооружении системы водоснабжения частного дома или дачи, трубы прокладывают от источника воды (колодца или скважины) до дома — под землей. И все равно, чтобы они не замерзли, требуется утепление. Рассчитать количество утеплителя можно зная площадь наружной поверхности трубопровода. Только в этом случае надо брать материал с солидным запасом — стыки должны перекрываться с солидным запасом.
Сечение трубы необходимо для определения пропускной способности — сможет ли данное изделие провести требуемое количество жидкости или газа. Этот же параметр часто нужен при выборе диаметра труб для отопления и водопровода, расчета производительности насоса и т.д.
Внутренний и наружный диаметр, толщина стенки, радиус
Трубы — специфический продукт.
Внутренний и наружный диаметр трубы, толщина стенки Они имеют внутренний и наружный диаметр, так как стенка у них толстая, ее толщина зависит от типа трубы и материала из которого она изготовлена. В технических характеристиках чаще указывают наружный диаметр и толщину стенки.
Они имеют внутренний и наружный диаметр, так как стенка у них толстая, ее толщина зависит от типа трубы и материала из которого она изготовлена. В технических характеристиках чаще указывают наружный диаметр и толщину стенки.Имея эти два значения, легко высчитать внутренний диаметр — от наружного отнять удвоенную толщину стенки: d = D — 2*S. Если у вас наружный диаметр 32 мм, толщина стенки 3 мм, то внутренний диаметр будет: 32 мм — 2 * 3 мм = 26 мм.
Если же наоборот, имеется внутренний диаметр и толщина стенки, а нужен наружный — к имеющемуся значению добавляем удвоенную толщину стеки.
С радиусами (обозначаются буквой R) еще проще — это половина от диаметра: R = 1/2 D. Например, найдем радиус трубы диаметром 32 мм. Просто 32 делим на два, получаем 16 мм.
Измерения штангенциркулем более точныеЧто делать, если технических данных трубы нет? Измерять. Если особая точность не нужна, подойдет и обычная линейка, для более точных измерений лучше использовать штангенциркуль.

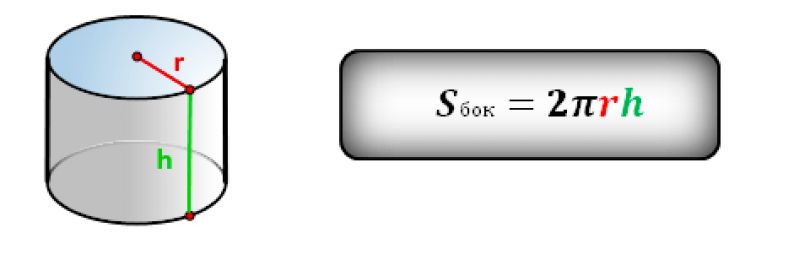
Расчет площади поверхности трубы
Труба представляет собой очень длинный цилиндр, и площадь поверхность трубы рассчитывается как площадь цилиндра. Для вычислений потребуется радиус (внутренний или наружный — зависит от того, какую поверхность вам надо рассчитать) и длина отрезка, который вам необходим.
Формула расчета боковой поверхности трубыЧтобы найти боковую площадь цилиндра, перемножаем радиус и длину, полученное значение умножаем на два, а потом — на число «Пи», получаем искомую величину. При желании можно рассчитать поверхность одного метра, ее потом можно умножать на нужную длину.
Для примера рассчитаем наружную поверхность куска трубы длиной 5 метров, с диаметром 12 см. Для начала высчитаем диаметр: делим диаметр на 2, получаем 6 см. Теперь все величины надо привести к одним единицам измерения. Так как площадь считается в квадратных метрах, то сантиметры переводим в метры. 6 см = 0,06 м. Дальше подставляем все в формулу: S = 2 * 3,14 * 0,06 * 5 = 1,884 м2.
 Если округлить, получится 1,9 м2.
Если округлить, получится 1,9 м2.Расчет веса
С расчетом веса трубы все просто: надо знать, сколько весит погонный метр, затем эту величину умножить на длину в метрах. Вес круглых стальных труб есть в справочниках, так как этот вид металлопроката стандартизован. Масса одного погонного метра зависит от диаметра и толщины стенки. Один момент: стандартный вес дан для стали плотностью 7,85 г/см2 — это тот вид, который рекомендован ГОСТом.
Таблица веса круглых стальных трубВ таблице Д — наружный диаметр, условный проход — внутренний диаметр, И еще один важный момент: указана масса обычных стального проката, оцинкованные на 3% тяжелее.
Таблица веса профилированной трубы квадратного сеченияКак высчитать площадь поперечного сечения
Формула нахождения площади сечения круглой трубыЕсли труба круглая, площадь сечения считать надо по формуле площади круга: S = π*R2. Где R — радиус (внутренний), π — 3,14. Итого, надо возвести радиус в квадрат и умножить его на 3,14.

Например, площадь сечения трубы диаметром 90 мм. Находим радиус — 90 мм / 2 = 45 мм. В сантиметрах это 4,5 см. Возводим в квадрат: 4,5 * 4,5 = 2,025 см2, подставляем в формулу S = 2 * 20,25 см2 = 40,5 см2.
Площадь сечения профилированной трубы считается по формуле площади прямоугольника: S = a * b, где a и b — длины сторон прямоугольника. Если считать сечение профиля 40 х 50 мм, получим S = 40 мм * 50 мм = 2000 мм2 или 20 см2 или 0,002 м2.
Как рассчитать объем воды в трубопроводе
При организации системы отопления бывает нужен такой параметр, как объем воды, которая поместится в трубе. Это необходимо при расчете количества теплоносителя в системе. Для данного случая нужна формула объема цилиндра.
Формула расчета объема воды в трубеТут есть два пути: сначала высчитать площадь сечения (описано выше) и ее умножить на длину трубопровода. Если считать все по формуле, нужен будет внутренний радиус и общая длинна трубопровода.
 Рассчитаем сколько воды поместится в системе из 32 миллиметровых труб длиной 30 метров.
Рассчитаем сколько воды поместится в системе из 32 миллиметровых труб длиной 30 метров.Сначала переведем миллиметры в метры: 32 мм = 0,032 м, находим радиус (делим пополам) — 0,016 м. Подставляем в формулу V = 3,14 * 0,0162 * 30 м = 0,0241 м3. Получилось = чуть больше двух сотых кубометра. Но мы привыкли объем системы измерять литрами. Чтобы кубометры перевести в литры, надо умножить полученную цифру на 1000. Получается 24,1 литра.
Калькулятор расчета объема и площади трубы
Инструкция для калькулятора онлайн расчета площади и объема трубы
Все параметры указываем в мм
L – Труба в длину.
D1 – Диаметр по внутренней части.
D2 – Диаметр по внешней части трубы.
При помощи данной программы, Вы сможете рассчитать объем воды или другой любой жидкости в трубе.
 2*L.
2*L.Где,
L— длина трубопровода.
R1— внутренний радиус.
R2— наружный радиус.
Как правильно выполняются вычисления объема тел
Расчет объема цилиндра, труб и других физических тел – классическая задача из прикладной науки и инженерной деятельности. Как правило, данная задача не является тривиальной. Согласно аналитическим формулам для вычисления объема жидкостей в различных телах и емкостях может оказаться очень затруднительным и громоздким. Но, в основном объем простых тел можно вычислить достаточно просто. К примеру, при помощи нескольких математических формул Вы сможете определить объем трубопровода. Как правило, количество жидкости в трубах определяется значением м3 или метры кубические. Однако в нашей программе, Вы получаете все расчеты в литрах, а площадь поверхности определяется в м2 – квадратных метрах.
Полезная информация
Размеры стальных трубопроводов для газоснабжения, отопления или водоснабжения указываются в целых дюймам (1″,2″) или его долях (1/2″, 3/4″).
 За 1″ согласно общепринятым меркам принимают 25,4 миллиметра. На сегодняшний день стальные трубы можно встретить в усиленном (с двойной стенкой) или в обычном исполнении.
За 1″ согласно общепринятым меркам принимают 25,4 миллиметра. На сегодняшний день стальные трубы можно встретить в усиленном (с двойной стенкой) или в обычном исполнении.Для усиленного и обычного трубопровода внутренние диаметры отличаются от стандартных – 25,4 миллиметра: так в усиленном, этот параметр составляет 25,5 миллиметров, а в стандартном или обычном – 27,1 миллиметр. Отсюда следует, что незначительно, но эти параметры отличаются, что тоже следует учесть при выборе труб для отопления или водоснабжения. Как правило, специалисты не особо вникают в эти подробности, так как для них важным условием является — Ду (Dn) или условный проход. Данная величина является безразмерной. Этот параметр можно определить с помощью специальных таблиц. Но нам не стоит вникать в эти подробности.
Стыковка различных стальных труб, размер которых представлен в дюймах с алюминиевыми, медными, пластиковыми и другими, данные которых представлены в миллиметрах, предусмотрены специальные переходники.

Как правило, данный вид расчета труб необходим в процессе вычисления размера расширительного бачка для отопительной системы. Объем воды в системе обогрева комнаты или дома, рассчитывается с помощью нашей программы в онлайн-режиме. Однако, зачастую, этими данными неопытные специалисты просто пренебрегают, что не стоит делать. Так как, для эффективного функционирования отопительной системы нужно учесть все параметры, чтобы правильно выбрать котел, насос и радиаторы. Также немаловажным объем жидкости в трубопроводе будет в том случае, когда вместо воды будет использовать антифриз в системе обогрева, который является достаточно дорогим и переплаты в этом случае будут излишни.
Чтобы определить объем жидкости необходимо правильно замерять наружный и внутренний диаметр трубопровода.
Важно! Не стоит пренебрегать результатами расчета при проектировании отопительной системы. В противном случае Вы рискуете не правильно выбрать котел по мощности, который будет неэффективным и неэкономичным в процессе эксплуатации, и как следствие помещения будут плохо обогреваться.

Примерный расчет можно выполнить исходя из пропорции 15 л жидкости на 1 кВт мощности отопительного котла
К примеру, у Вас котел на 4 кВт, отсюда получаем объем всей системы равен 60 литров (4х15)
Мы привели точные значения объема жидкости для разных радиаторов в системе отопления.
Объем воды:
- старая чугунная батарея в 1 секции – 1,7 литра;
- новая чугунная батарея в 1 секции – 1 литр;
- биметаллический радиатор в 1 секции – 0,25 литра;
- алюминиевый радиатор в 1 секции – 0,45 литра.
Заключение
Теперь Вы знаете, как можно правильно и быстро вычислить объем трубы для водоснабжения или системы отопления.
Трубный калькулятор веса круглой трубы
Расчет веса погонного метра круглой трубы из различных металлов, таблицы веса и дополнительные расчеты стоимости по весу, длине и другим параметрам
Формула и способы рассчета
Расчет веса трубы из различных металлов (стальные трубы, нержавеющие, медные и др.
 ) производится на основе имеющихся в справочниках ГОСТ и ТУ данных. Вес метра трубы, сортамент которой не входит в имеющиеся на сайте справочники, рассчитывается онлайн по формуле m = Pi * ro * S * (D — S) * L; Pi — математическая константа, которая выражает отношение длины окружности к её диаметру, равная ~3.14; ro — плотность металла из которой изготовлена круглая труба в кг/м³; Для расчета удельного веса 1 погонного метра трубы (m) необходимо указать размеры профиля трубы: диаметр D в мм, а также толщину металла, из которого изготовлена труба (толщину стенки S) и длину L (по умолчанию 1 м). Расчет теоретического веса прямоугольной профильной трубы производится аналогично круглой, за исключением части формулы для определения площади поперечного сечения.
) производится на основе имеющихся в справочниках ГОСТ и ТУ данных. Вес метра трубы, сортамент которой не входит в имеющиеся на сайте справочники, рассчитывается онлайн по формуле m = Pi * ro * S * (D — S) * L; Pi — математическая константа, которая выражает отношение длины окружности к её диаметру, равная ~3.14; ro — плотность металла из которой изготовлена круглая труба в кг/м³; Для расчета удельного веса 1 погонного метра трубы (m) необходимо указать размеры профиля трубы: диаметр D в мм, а также толщину металла, из которого изготовлена труба (толщину стенки S) и длину L (по умолчанию 1 м). Расчет теоретического веса прямоугольной профильной трубы производится аналогично круглой, за исключением части формулы для определения площади поперечного сечения.Популярные размеры круглых труб в России
- 108х4
- 530х8
- 325х8
- 57х3.5
- 219х6
Таблицы веса метра круглых труб различных металлов и сплавов по всем доступным ГОСТ и ТУ
Посмотреть все данные по этому виду металлопроката в
Круглая труба
полной таблице веса:Стандарты ГОСТ и ТУ доступные в расчетах калькулятора и таблицах веса:
- ГОСТ 494-2014 (х/д) — Трубы латунные.
 Холоднодеформированные
Холоднодеформированные - ГОСТ 9941-81 — Трубы бесшовные холодно- и тепло-деформированные из коррозионно-стойкой стали
- ГОСТ 10707-80 — Трубы стальные электросварные холоднодеформированные
- ГОСТ 494-2014 (п) — Трубы латунные. Прессованные
- ГОСТ 617-2006 (п) — Трубы медные и латунные круглого сечения общего назначения. Прессованные
- ГОСТ 3262-75 — Трубы стальные водогазопроводные. Оцинкованные
- ГОСТ Р 52318-2005 — Трубы медные круглого сечения для воды и газа
- ГОСТ 32598-2013 — Трубы медные круглого сечения для воды и газа
- ГОСТ 617-2006 (х/д) — Трубы медные и латунные круглого сечения общего назначения. Холоднодеформированные
- ГОСТ 10704-91 — Трубы стальные электросварные прямошовные
- ГОСТ 18482-2018 — Трубы прессованные из алюминия и алюминиевых сплавов
Применение
Вес погонного метра трубы очень часто необходимо знать для осуществления расчетов в металлоконструкциях. Самое частое использование трубного калькулятора — определение массы трубы в приобретаемой партии, чтобы выяснить необходимые габариты транспорта для её перевозки, а также для расчета нагрузок будущей металлоконструкции и стоимости продукции.

Как посчитать объем трубы при выборе расширительного мембранного бака.
Как посчитать объем трубы.
Данные вычисления требуются для определения объёма системы отопления, при выборе расширительного мембранного бака.
Объём расширительного мембранного бака подбирается из расчета не менее 10% от всего литража системы.Определите радиус трубы R. Если необходимо рассчитать внутренний объем трубы, то надо найти внутренний радиус. Если необходимо рассчитать объем, занимаемый трубой, следует рассчитать радиус внешний. Путем измерений можно легко получить диаметр (как внутренний, так и внешний) и длину окружности сечения трубы. Если известен диаметр трубы, поделите его на два. Так, R=D/2, где D — диаметр. Если известна длина окружности сечения трубы, поделите его на 2*Пи, где Пи=3.14159265. Так, R=L/6,28318530, где L — длина окружности.
Найдите площадь сечения трубы. Возведите значение радиуса в квадрат и помножьте его на число Пи.
 Так, S=Пи*R*R, где R — радиус трубы. Площадь сечения будет найдена в той же системе единиц, в которой было взято значение радиуса. Например, если значение радиуса представлено в сантиметрах, то площадь сечения будет вычислена в квадратных сантиметрах.
Так, S=Пи*R*R, где R — радиус трубы. Площадь сечения будет найдена в той же системе единиц, в которой было взято значение радиуса. Например, если значение радиуса представлено в сантиметрах, то площадь сечения будет вычислена в квадратных сантиметрах.Вычислите объем трубы. Помножьте площадь сечения трубы на нее длину. Объем трубы V=S*L, где S — площадь сечения, а L — длина трубы.
Программа расчета объема воды в трубе и радиаторах
Внутренний диаметр трубы, мм. = объём секции радиатора, литров = Длина трубы, м = количество секций радиатора, шт. = Объем воды в трубе, м³ = объём воды в радиаторе, м³ = Объем воды в трубе, литров = объём воды в радиаторе, литров = Объем воды в системе, м³ = Объем воды в системе, литров =
Таблица объёма жидкости в одном метре трубы:Внутренний диаметр,
ммВнутренний объем 1 м погонного трубы,
литровВнутренний диаметр,
ммВнутренний объем 1 м погонного трубы,
литров4
0,0126
105
8,6590
5
0,0196
110
9,5033
6
0,0283
115
10,3869
7
0,0385
120
11,3097
8
0,0503
125
12,2718
9
0,0636
130
13,2732
10
0,0785
135
14,3139
11
0,0950
140
15,3938
12
0,1131
145
16,5130
13
0,1327
150
17,6715
14
0,1539
160
20,1062
15
0,1767
170
22,6980
16
0,2011
180
25,4469
17
0,2270
190
28,3529
18
0,2545
200
31,4159
19
0,2835
210
34,6361
20
0,3142
220
38,0133
21
0,3464
230
41,5476
22
0,3801
240
45,2389
23
0,4155
250
49,0874
24
0,4524
260
53,0929
26
0,5309
270
57,2555
28
0,6158
280
61,5752
30
0,7069
290
66,0520
32
0,8042
300
70,6858
34
0,9079
320
80,4248
36
1,0179
340
90,7920
38
1,1341
360
101,7876
40
1,2566
380
113,4115
42
1,3854
400
125,6637
44
1,5205
420
138,5442
46
1,6619
440
152,0531
48
1,8096
460
166,1903
50
1,9635
480
180,9557
52
2,1237
500
196,3495
54
2,2902
520
212,3717
56
2,4630
540
229,0221
58
2,6421
560
246,3009
60
2,8274
580
264,2079
62
3,0191
600
282,7433
64
3,2170
620
301,9071
66
3,4212
640
321,6991
68
3,6317
660
342,1194
70
3,8485
680
363,1681
72
4,0715
700
384,8451
74
4,3008
720
407,1504
76
4,5365
740
430,0840
78
4,7784
760
453,6460
80
5,0265
780
477,8362
82
5,2810
800
502,6548
84
5,5418
820
528,1017
86
5,8088
840
554,1769
88
6,0821
860
580,8805
90
6,3617
880
608,2123
92
6,6476
900
636,1725
94
6,9398
920
664,7610
96
7,2382
940
693,9778
98
7,5430
960
723,8229
100
7,8540
980
754,2964
—
—
1000
785,3982
Калькулятор площади
Используйте калькуляторы ниже, чтобы вычислить площадь поверхности нескольких распространенных форм.

Площадь поверхности мяча
Площадь поверхности конуса
Площадь поверхности куба
Площадь поверхности цилиндрического резервуара
Площадь прямоугольного резервуара
Площадь поверхности капсулы
Площадь поверхности крышки
Для расчета укажите любые два значения ниже.
Площадь поверхности конической усадки
Площадь поверхности эллипсоида
Площадь квадратной пирамиды
Калькулятор связанных объемов | Калькулятор площади | Калькулятор площади поверхности телаПлощадь поверхности твердого тела — это мера общей площади, занимаемой поверхностью объекта.
 Все объекты, рассматриваемые в этом калькуляторе, более подробно описаны на страницах «Калькулятор объема» и «Калькулятор площади». Таким образом, этот калькулятор будет сосредоточен на уравнениях для расчета площади поверхности объектов и использовании этих уравнений. Пожалуйста, обратитесь к вышеупомянутым калькуляторам для получения более подробной информации по каждому отдельному объекту.
Все объекты, рассматриваемые в этом калькуляторе, более подробно описаны на страницах «Калькулятор объема» и «Калькулятор площади». Таким образом, этот калькулятор будет сосредоточен на уравнениях для расчета площади поверхности объектов и использовании этих уравнений. Пожалуйста, обратитесь к вышеупомянутым калькуляторам для получения более подробной информации по каждому отдельному объекту.Сфера
Площадь поверхности (SA) сферы можно рассчитать по формуле:
SA = 4πr 2
где r — радиусКсаэль не любит ни с кем делиться шоколадными трюфелями.Когда она получает коробку трюфелей Lindt, она приступает к вычислению площади поверхности каждого трюфеля, чтобы определить общую площадь поверхности, которую она должна лизать, чтобы уменьшить вероятность того, что кто-то попытается съесть ее трюфели. Учитывая, что каждый трюфель имеет радиус 0,325 дюйма:
SA = 4 × π × 0,325 2 = 1,327 дюйм 2
Конус
Площадь поверхности круглого конуса может быть вычислена путем суммирования площадей поверхности каждого из его отдельных компонентов.
 «Базовая SA» относится к кругу, который содержит основание в замкнутом круговом конусе, в то время как боковая SA относится к остальной части конуса между основанием и его вершиной. Уравнения для расчета каждого из них, а также общая SA замкнутого кругового конуса показаны ниже:
«Базовая SA» относится к кругу, который содержит основание в замкнутом круговом конусе, в то время как боковая SA относится к остальной части конуса между основанием и его вершиной. Уравнения для расчета каждого из них, а также общая SA замкнутого кругового конуса показаны ниже:основание SA = πr 2
боковая SA = πr√r 2 + h 2
общая SA = πr (r + √r 2 + h 2 )
где r — радиус, а h — высотаАфина недавно заинтересовалась культурой Юго-Восточной Азии, и ее особенно очаровала коническая шляпа, обычно называемая «рисовой шляпой», которая обычно используется в ряде стран Юго-Восточной Азии.Она решает сделать свое собственное и, будучи очень практичным человеком, не погрязшим в сентиментальности, достает свадебное платье своей матери из темных уголков гардероба, в котором оно находится. Она определяет площадь поверхности материала, необходимого для создания шляпы, радиусом 1 фут и высотой 0,5 фута следующим образом:
боковая SA = π × 0,4√0,4 2 + 0,5 2 = 0,805 фута 2
Куб
Площадь поверхности куба может быть вычислена путем суммирования общих площадей его шести квадратных граней:
SA = 6a 2
где a — длина кромкиЭнн хочет подарить своему младшему брату кубик Рубика на его день рождения, но знает, что у ее брата мало внимания и он легко разочаровывается.
 Она заказывает кубик Рубика, у которого все грани черные, и должна платить за настройку в зависимости от площади поверхности куба с длиной ребра 4 дюйма.
Она заказывает кубик Рубика, у которого все грани черные, и должна платить за настройку в зависимости от площади поверхности куба с длиной ребра 4 дюйма.SA = 6 × 4 2 = 96 дюймов 2
Цилиндрический бак
Площадь поверхности закрытого цилиндра может быть вычислена путем суммирования общих площадей его основания и боковой поверхности:
база SA = 2πr 2
боковой SA = 2πrh
общая SA = 2πr (r + h) где r — радиус, а h — высотаУ Джереми есть большой цилиндрический аквариум, в котором он купается, потому что он не любит душ или ванну.Ему любопытно, остывает ли его нагретая вода быстрее, чем в ванне, и ему нужно рассчитать площадь поверхности его цилиндрического резервуара высотой 5,5 футов и радиусом 3,5 фута.
всего SA = 2π × 3,5 (3,5 + 5,5) = 197,920 футов 2
Прямоугольный бак
Площадь прямоугольного резервуара равна сумме площадей каждой из его граней:
SA = 2lw + 2lh + 2wh
.
где l — длина, w — ширина, а h — высота
Банан, старшая дочь в длинной череде фермеров, выращивающих бананы, хочет преподать своей испорченной гнилой младшей сестре Банановый хлеб урок о надеждах и ожиданиях.Banana-Bread всю неделю настаивает на том, чтобы ей нужен новый набор ящиков для размещения ее новых фигурок Бэтмена. Таким образом, Банана покупает ей большой кукольный домик Барби с кухонной утварью ограниченного выпуска, духовкой, фартуком и реалистичными гниющими бананами для Бэтмена. Она упаковывает их в прямоугольную коробку таких же размеров, как выдвижной ящик, который нужен Banana-Bread, и ей нужно определить количество оберточной бумаги, необходимое для завершения презентации подарка сюрприза размером 3 фута × 4 фута × 5 футов:
SA = (2 × 3 × 4) + (2 × 4 × 5) + (2 × 3 × 5) = 94 футов 2
Капсула
Площадь поверхности капсулы может быть определена путем комбинирования уравнений площади поверхности для сферы и площади боковой поверхности цилиндра.Обратите внимание, что площадь поверхности оснований цилиндра не включена, поскольку она не составляет часть площади поверхности капсулы.
 Общая площадь рассчитывается следующим образом:
Общая площадь рассчитывается следующим образом:SA = 4πr 2 + 2πrh
где r — радиус, а h — высотаГорацио производит плацебо, которое призвано оттачивать индивидуальность человека, критическое мышление и способность объективно и логически подходить к различным ситуациям.Он уже протестировал рынок и обнаружил, что подавляющее большинство выборочной совокупности не проявляют ни одного из этих качеств и очень готовы купить его продукт, еще больше укрепляя свои черты, от которых они так отчаянно стремятся избавиться. Горацио необходимо определить площадь поверхности каждой капсулы, чтобы он мог покрыть их чрезмерным слоем сахара и обратиться к предрасположенным к сахару языкам населения при подготовке к его следующему плацебо, которое «лечит» все формы сахарного диабета.Учитывая, что каждая капсула имеет r 0,05 дюйма и h 0,5 дюйма:
SA = 4π × 0,05 2 + 2π × 0,05 × 0,5 = 0,188 дюйма 2
Сферический колпачок
Площадь поверхности сферической крышки зависит от высоты рассматриваемого сегмента.
 Предоставленный калькулятор предполагает твердую сферу и включает основание крышки при расчете площади поверхности, где общая площадь поверхности является суммой площади основания и боковой поверхности сферической крышки.Если вы используете этот калькулятор для вычисления площади поверхности полой сферы, вычтите площадь поверхности основания. Учитывая два значения высоты, радиуса крышки или радиуса основания, третье значение можно рассчитать с помощью уравнений, представленных в Калькуляторе объема. Уравнения площади поверхности следующие:
Предоставленный калькулятор предполагает твердую сферу и включает основание крышки при расчете площади поверхности, где общая площадь поверхности является суммой площади основания и боковой поверхности сферической крышки.Если вы используете этот калькулятор для вычисления площади поверхности полой сферы, вычтите площадь поверхности основания. Учитывая два значения высоты, радиуса крышки или радиуса основания, третье значение можно рассчитать с помощью уравнений, представленных в Калькуляторе объема. Уравнения площади поверхности следующие:сферический колпачок SA = 2πRh
база SA = πr 2
Полная твердая сфера SA = 2πRh + πr 2
где R — радиус сферической крышки, r — радиус основания, а h — высотаДженнифер завидует земному шару, который ее старший брат Лоуренс получил на свой день рождения.Поскольку Дженнифер на две трети старше своего брата, она решает, что заслуживает одну треть земного шара своего брата.
 Вернув ручную пилу своего отца в сарай для инструментов, она вычисляет площадь поверхности своей полой части земного шара с R 0,80 фута и h 0,53 фута, как показано ниже:
Вернув ручную пилу своего отца в сарай для инструментов, она вычисляет площадь поверхности своей полой части земного шара с R 0,80 фута и h 0,53 фута, как показано ниже:SA = 2π × 0,80 × 0,53 = 2,664 фута 2
Коническая усадьба
Площадь поверхности твердого прямоугольного усеченного конуса равна сумме площадей его двух круглых концов и площади его боковой поверхности:
круговой конец SA = π (R 2 + r 2 )
боковой SA = π (R + r) √ (R-r) 2 + h 2
всего SA = π (R 2 + r 2 ) + π (R + r) √ (R-r) 2 + h 2
где R и r — радиусы концов, h — высотаПол делает вулкан в форме усеченного конуса для своего проекта научной ярмарки.Пол рассматривает извержения вулканов как явление насилия и, выступая против всех форм насилия, решает сделать свой вулкан в форме закрытой конической усеченной пирамиды, которая не извергается.
 Хотя его вулкан вряд ли произведет впечатление на судей научной ярмарки, Пол все же должен определить площадь поверхности материала, которую ему нужно покрыть внешнюю стену своего вулкана с R на 1 фут, на на 0,3 фута и на . 1,5 фута:
Хотя его вулкан вряд ли произведет впечатление на судей научной ярмарки, Пол все же должен определить площадь поверхности материала, которую ему нужно покрыть внешнюю стену своего вулкана с R на 1 фут, на на 0,3 фута и на . 1,5 фута:всего SA = π (1 2 + 0,3 2 ) + π (1 + 0.3) √ (1 — 0,3) 2 + 1,5 2 = 10,185 футов 2
Эллипсоид
Для вычисления площади поверхности эллипсоида нет простой и точной формулы, такой как куб или другая более простая форма. В калькуляторе выше используется приблизительная формула, предполагающая, что эллипсоид почти сферический:
SA ≈ 4π 1,6 √ (a 1,6 b 1,6 + a 1,6 c 1,6 + b 1,6 c 1,6 ) / 3
где a , b и c — оси эллипсаКолтен всегда любил готовить и недавно выиграл на конкурсе керамический нож.
 К несчастью для своей семьи, которая почти полностью ест мясо, Колтейн практиковал свою технику нарезки чрезмерного количества овощей. Вместо того, чтобы есть овощи, отец Колтейна уныло смотрит на свою тарелку и оценивает площадь поверхности эллиптических разрезов кабачков с помощью топоров 0,1, 0,2 и 0,35 дюйма:
К несчастью для своей семьи, которая почти полностью ест мясо, Колтейн практиковал свою технику нарезки чрезмерного количества овощей. Вместо того, чтобы есть овощи, отец Колтейна уныло смотрит на свою тарелку и оценивает площадь поверхности эллиптических разрезов кабачков с помощью топоров 0,1, 0,2 и 0,35 дюйма:SA ≈ 4π 1,6 √ (0,1 1,6 0,2 1,6 + 0,1 1,6 0,35 1,6 + 0,2 1,6 0,35 1.6 ) / 3 = 0,562 дюйма 2
Квадратная пирамида
Площадь поверхности квадратной пирамиды состоит из площади ее квадратного основания и площади каждой из четырех треугольных граней. Учитывая высоту h и длину кромки a , площадь поверхности можно рассчитать с помощью следующих уравнений:
база SA = a 2
боковая SA = 2a√ (a / 2) 2 + h 2
всего SA = a 2 + 2a√ (a / 2) 2 + h 2В классе Вонквайлы недавно завершено строительство модели Великой пирамиды в Гизе.
 Тем не менее, она считает, что модель не излучает того архитектурного чуда, как оригинал, и решает, что покрытие ее «снегом», по крайней мере, придаст вид чуда. Она вычисляет площадь поверхности расплавленного сахара, которая потребуется ей, чтобы полностью покрыть пирамиду, с длиной ребра a 3 фута и высотой h 5 футов:
Тем не менее, она считает, что модель не излучает того архитектурного чуда, как оригинал, и решает, что покрытие ее «снегом», по крайней мере, придаст вид чуда. Она вычисляет площадь поверхности расплавленного сахара, которая потребуется ей, чтобы полностью покрыть пирамиду, с длиной ребра a 3 фута и высотой h 5 футов:всего SA = 3 2 + 2 × 3√ (3/2) 2 + 5 2 = 40,321 футов 2
В отличие от Великой пирамиды в Гизе, которая простояла тысячи лет, ее модель, сделанная из крекеров и покрытая сахаром, просуществовала всего несколько дней.
Единицы общего пользования
Единица метр 2 километр 2 1,000,000 сантиметр 2 0,0001 микрометр 0,000000000001 га 10,000 миля 2 2,589,990 ярд 2 0.  83613
83613футов 2 0,092903 дюймов 2 0,00064516 акров 4,046 Площадь круга Площадь круга — Калькулятор площади круга
— Площадь круга
Чтобы понять, как рассчитать квадратные метры, мы должны сначала начать с определения площади. Площадь — это размер двумерной поверхности. Площадь круга — это пространство внутри его окружности (внешнего периметра).2) квадрат
Сокращения единиц площади: фут 2 , дюйм 2 , ярд 2 , см 2 , мм 2 , м 2Где это нужно в повседневной жизни?
Наш калькулятор квадратных метров поможет вам рассчитать площадь, необходимую для создания круглых ландшафтных дизайнов, ковровых покрытий, наклеек на стены, центральной лепнины на потолке и напольной плитки.

Легко найти площадь круга (и связанные варианты использования)
Технологии продвинулись вперед, и благодаря этому появилось много калькуляторов, которые помогают пользователям точно измерять вещи даже не выходя из своего ноутбука или мобильного телефона.Наш калькулятор площади круга позволяет вам легко найти площадь, длину окружности, радиус или конкретный диаметр любого круга.
Все, что вам нужно сделать, это полностью понять переменные этой формулы, включая:
- r (радиус)
- d (диаметр)
- C (окружность)
- А (площадь)
- π = пи = 3,1415926535898
- √ = квадратный корень
С помощью любой из этих переменных (A, C, r или d) окружности вы можете точно измерить три других неизвестных.Вы можете использовать эту формулу во многих реальных примерах, таких как строительство дома, сверление, заполнение отверстий бетоном и т. Д. По сути, формула дает вам точную информацию о том, сколько материала вам нужно или насколько велика поверхность (в которую вы будете просверливать) должно быть.

Тем не менее, вы также должны знать, что вычислитель площади круга требует других вещей, которые вам нужно знать перед измерением.
Что нужно позаботиться об измерении площади круга.
Круги сложной формы. Пожалуй, их главная переменная — радиус, который измеряется от центра круга до любой из его сторон. По сути, диаметр в два раза больше радиуса — или любой линии, идущей от одной стороны круга к другой, пересекая его центр.
Окружность круга, однако, многими не так понятна. По сути, эту переменную можно определить как расстояние по окружности или всю длину контура по окружности.
Переменная π (pi) — это, по сути, константа, которую нельзя выразить в виде дроби, но она применяется ко всем вычислениям, включая вычислитель площади круга, тогда как √ (квадратный фут) — это, по сути, общая поверхность внутри круга.
Все эти переменные, используемые со времен древней геометрии, позволяют точно вычислить все, что связано с кругом.
 Однако вместо того, чтобы делать что-то вручную, теперь вы можете использовать наш калькулятор площади круга и формулу готового круга.
Однако вместо того, чтобы делать что-то вручную, теперь вы можете использовать наш калькулятор площади круга и формулу готового круга.Решите общую задачу геометрии сегодня с помощью нашего калькулятора площади круга.
Независимо от того, занимаетесь ли вы в классе и решаете тест по математике или вам нужен точный расчет площади круга для проекта, который вы строите, формула для площади круга проста, но не так проста, когда у вас остается ручка. и бумага.
Вот почему и как наш калькулятор площади круга может помочь вам и мгновенно решить ваши вопросы. Все, что вам нужно, это еще одна переменная, чтобы получить остальные три и немедленно решить проблему.
Теперь вы, наконец, можете использовать и применять калькулятор площади круга повсюду — и быстро получать нужную информацию — не ходя по кругу!
Какие измерения вам нужны?
Вам необходимо знать диаметр круга в футах (футах), дюймах (дюймах), ярдах (ярдах), сантиметрах (см), миллиметрах (мм) или метрах (м).

Что можно рассчитать с помощью этого инструмента?
Вы можете рассчитать площадь границы круга в квадратных футах, квадратных дюймах, квадратных ярдах, квадратных сантиметрах, квадратных миллиметрах и квадратных метрах.Да, наш инструмент такой классный.
Наш калькулятор дает возможность рассчитать точную стоимость материалов. Все, что вам нужно сделать, это ввести цену за единицу площади и вуаля, вы получите полную стоимость материалов в один клик!
Коэффициенты пересчета:
Для преобразования квадратных футов, квадратных дюймов, квадратных ярдов, квадратных сантиметров, квадратных миллиметров и квадратных метров вы можете использовать следующую таблицу преобразования.
Квадратные футы в квадратные ярды умножить футы 2 на 0.11111, чтобы получить ярд 2 Квадратные футы в квадратные метры умножьте футы 2 на 0,092903, чтобы получить м 2 Квадратные ярды в квадратные футы умножьте ярды 2 на 9, чтобы получить футы 2 Квадратные ярды в квадратные метры умножьте ярд 2 на 0,836127, чтобы получить m 2 Квадратные метры в квадратные футы умножить m 2 на 10.  7639, чтобы получить футов 2
7639, чтобы получить футов 2 Квадратные метры в квадратные ярды умножьте m 2 на 1,19599, чтобы получить ярд 2 Квадратные метры в квадратные миллиметры умножьте значение m 2 на 1000000, чтобы получить мм 2 Квадратные метры в квадратные сантиметры умножьте значение m 2 на 10000, чтобы получить cm 2 Квадратные сантиметры в квадратные метры умножьте значение cm 2 на 0.0001, чтобы получить мм 2 Квадратные сантиметры в квадратные миллиметры умножьте значение 2 на 100, чтобы получить мм 2 Квадратные миллиметры в квадратные сантиметры умножьте значение 2 на 0,000001, чтобы получить 2 Квадратные миллиметры в квадратные метры умножьте значение 2 на 1000000, чтобы получить m 2 Калькулятор объема трубы
Этот калькулятор объема трубы оценивает объем трубы, а также массу жидкости, которая течет по ней.
 Этот калькулятор — полезный инструмент для всех, кому нужно знать точный объем воды в трубе. Вам будет полезно, например, если вы проектируете систему полива для своего сада. Продолжайте читать, чтобы узнать, что такое цилиндр, найдите формулу объема трубы и проверьте «руководство пользователя» для правильных расчетов в калькуляторе объема трубы.
Этот калькулятор — полезный инструмент для всех, кому нужно знать точный объем воды в трубе. Вам будет полезно, например, если вы проектируете систему полива для своего сада. Продолжайте читать, чтобы узнать, что такое цилиндр, найдите формулу объема трубы и проверьте «руководство пользователя» для правильных расчетов в калькуляторе объема трубы.Калькулятор объема трубы
Знание объема трубы может быть полезно по многим причинам. Это будет выгодно как владельцам частных домов, так и инженерам-строителям.Например, вы можете узнать водоемкость вашей системы отопления дома или поинтересоваться, хватит ли выбранного вами диаметра трубы для наполнения садового пруда.
Именно поэтому мы создали калькулятор объема трубы. Этот инструмент позволяет узнать объем конкретной трубы и вес воды (или другой жидкости) внутри нее. Он прост в использовании и эффективен. Все, что вам нужно сделать, это ввести размер трубы — ее внутренний диаметр
 Неважно, используете ли вы метрическую или британскую систему единиц, потому что вы можете свободно переключаться между ними с помощью раскрывающегося списка.
Неважно, используете ли вы метрическую или британскую систему единиц, потому что вы можете свободно переключаться между ними с помощью раскрывающегося списка.По умолчанию расчет веса жидкости производится для воды (ее плотность равна 997 кг / м³). Если вам нужно выполнить расчеты для другой жидкости, введите плотность вашей конкретной жидкости.
Ниже мы подготовили объяснение формулы объема трубы и пошаговый пример расчетов, чтобы показать вам, как правильно использовать калькулятор объема трубы.
Объем трубы — формула
По форме труба представляет собой полый цилиндр. Но что такое цилиндр? Мы можем видеть их вокруг себя каждый день. Это твердое тело с двумя основаниями, обычно круглыми, всегда конгруэнтными и параллельными друг другу. Развернутая сторона цилиндра образует прямоугольник. Высота цилиндра — это расстояние между основаниями (в случае трубы — это ее длина). Радиус цилиндра — это радиус его основания. Имейте в виду, что когда у вас есть цилиндр, диаметр равен удвоенному радиусу.
 Итак, для расчетов нужно диаметр уменьшить вдвое.
Итак, для расчетов нужно диаметр уменьшить вдвое.Круглый полый цилиндр, где R — радиус, r — внутренний радиус, h — высота.
Объем трехмерного твердого тела — это размер пространства, которое оно занимает. Для трубы это внутренний объем (вместо внешнего нужно брать внутренний диаметр). Чтобы выразить объем, мы используем кубические единицы (для метрических см³, дм³, м³ и для британских дюймов³ и ft³). Чтобы получить правильные результаты, последовательно используйте одну единицу на протяжении всего вычисления.
Формула объема цилиндра:
объем цилиндра = π * радиус² * высота.Для трубы используйте ее длину вместо высоты:
объем трубы = π * радиус² * длина, гдерадиус = внутренний диаметр / 2. Объем трубы равен объему жидкости внутри (если труба полностью заполнена ею). Масса жидкости берется из формулы преобразованной плотности. Итак, соответственно:масса жидкости = объем * плотность жидкости.
Объем воды в трубе — пример расчета
Давайте посмотрим, как правильно пользоваться калькулятором объема трубы. Для примера расчета нам понадобится несколько предположений. Рассчитаем объем трубы длиной 6 метров, внутренним диаметром 15 сантиметров. Труба используется для транспортировки воды. Поместим эти данные в калькулятор, чтобы найти объем воды в трубе, а также ее массу.
- Сначала введите диаметр трубы:
внутренний диаметр = 15 см. - Затем введите его длину:
длина = 6 м. - Нажмите кнопку расширенного режима и проверьте плотность жидкости. Значение по умолчанию установлено для воды, поэтому в нашем случае оно верное.
Плотность жидкости = 997 кг / м³. - Теперь вам доступны результаты расчета: объем
= 0,106 м³и масса жидкости= 105,71 кг.
Уравнения трубы
Поперечное сечение внутри участка трубы
Внутреннее поперечное сечение трубы можно рассчитать как
A i = π (d i /2) 2
= π d i 2 /4 (1)
, где
A i = внутреннее сечение трубы (м 2 2 )
d i = внутренний диаметр (м, дюйм)
Площадь поперечного сечения стенки трубы
Площадь поперечного сечения стенки или площадь материала трубопровода можно рассчитать как
A м = π (d o /2) 2 — π (d i /2) 2
= π ( d o 2 — d i 2 ) / 4 (2)
где
A м = площадь поперечного сечения стенки трубы (м 2 , дюйм 2 )
d o = внешний диаметр (м, дюйм)
Вес пустых труб
Вес пустых труб на единицу длины можно рассчитать как
w p = ρ м A м
= ρ м ( π (d o /2) 2 — /2) 2 )
= ρ м π (d o 2 — d i 2 ) (3)
где
w p = вес пустой трубы на единицу длины (кг / м, фунт / дюйм)
ρ s = плотность материала трубы (кг / м 3 , фунт / дюйм 3 )
Вес жидкости в трубах
Вес жидкости в трубах на единицу длины можно рассчитать как
w л = ρ л A
= ρ л π (d i /2)
где
w л = вес жидкости в трубе на единицу длины трубы (кг, фунт)
ρ л = плотность жидкости (кг / м 3 , фунт / дюйм 3 )
Вес трубы, заполненной жидкостью
Вес трубы, заполненной жидкостью на единицу длины, можно рассчитать как
w = w l + w p (5)
где
w = вес трубы и жидкости на единицу длины трубы (кг, фунты)
Наружная поверхность труб
Наружная поверхность стальных труб на единицу длины может быть рассчитана как
A o = 2 π (d o /2)
= π d o (6)
где
A 9 0816 o = внешняя площадь трубы — на единицу длины трубы (м 2 , в 2 )
Площадь внутренней поверхности труб
Площадь внутренней поверхности стальных труб на единицу длины можно рассчитать как
A i = 2 π (d i /2)
= π d i (7)
где
внутри A площадь трубы — на единицу длины трубы (м 2 , в 2 ) Формулы труб
Онлайн-калькулятор формул трубы
Калькулятор основан на формулах и уравнениях трубопровода, приведенных ниже.

Момент инерции
Момент инерции можно выразить как
I = π (d o 4 — d i 4 ) / 64
≈ 0,0849 o 4 — d i 4 ) (1)где
I = момент инерции (дюйм 4 )
d o = внешний диаметр )
d i = внутренний диаметр (дюймы)
Модуль упругости сечения
Модуль упругости сечения можно выразить как
S = 0.0982 (d o 4 — d i 4 ) / d o (2)
где
S = модуль упругости (дюйм 3
124)
Модуль сечения — это геометрическое свойство данного поперечного сечения, используемое при проектировании балок или изгибаемых элементов.
Поперечная площадь металла
Поперечная площадь металла может быть выражена как
A м = π (d o 2 — d i 2 ) / 4 (3)
83
909 где
A м = поперечная площадь металла (в 2 )
Внешняя поверхность трубы
Внешняя поверхность трубы или трубы на фут длины может быть выражена как
A o = π d o /12 (4)
где
A o = площадь внешней поверхности трубы (футы 2 на фут трубы)
Внутренняя поверхность трубы
Внутренняя труба или труба площадь поверхности на фут длины может быть выражена как
A i = π d i /12 (5)
, где
A i = площадь внутренней поверхности трубы (футы 2 на фут трубы)
Поперечная внутренняя площадь
Поперечная внутренняя площадь может быть выражена как
A a = 0.
 7854 d i 2 (6)
7854 d i 2 (6) где
A a = поперечная внутренняя площадь (в 2 )
Окружность Внешняя
Внешняя окружность может быть выражена как 9
C e = π d o (7)
где
C e = внешняя окружность (дюймы)
Окружность Внутренняя
Внутренняя окружность может быть выражена как
C i = π d i (8)
где
C i = внутренняя окружность (дюймы)
Расчет окружности трубы и площади сечения
Что такое площадь и периметр круга?
Набор точек на плоскости, одинаково удаленных от заданной точки $ O $, представляет собой окружность.Точка $ O $ называется центром окружности. Расстояние от центра круга до любой точки на окружности называется радиусом этого круга.
 Радиус круга должен быть положительным вещественным числом. Окружность с центром $ O $ и радиусом $ r $ обозначается $ c (O, r) $.
Радиус круга должен быть положительным вещественным числом. Окружность с центром $ O $ и радиусом $ r $ обозначается $ c (O, r) $.
Расстояние вокруг круга называется периметром или окружностью круга. Обычно обозначается как $ C $.
Если все вершины многоугольника принадлежат окружности, многоугольник называется вписанным. Если все стороны многоугольника касаются окружности, то многоугольник называется описанным.Метод определения длины окружности: Впишем в круг правильный многоугольник, например квадрат. Затем удвойте количество сторон этого многоугольника, чтобы получить восьмиугольник. Если продолжить процесс удвоения количества сторон правильные вписанные многоугольники, мы получаем бесконечную последовательность периметров правильных многоугольников, которая увеличивается. Эта возрастающая последовательность ограничена, поскольку периметры всех вписанных выпуклых многоугольников меньше периметра любого описанного многоугольника.Итак, эта возрастающая последовательность периметров имеет определенный предел.
 Этот предел — окружность. Следовательно, окружность окружности — это предел периметра правильного многоугольника, вписанного в окружность, когда число его вершин бесконечно удваивается. Поскольку все круги похожи, отношение длины окружности к диаметру одинаковое для всех кругов. Это отношение длины окружности к диаметру обозначается греческой буквой $ \ pi \ приблизительно 3,14 $. Таким образом, формула длины окружности
Этот предел — окружность. Следовательно, окружность окружности — это предел периметра правильного многоугольника, вписанного в окружность, когда число его вершин бесконечно удваивается. Поскольку все круги похожи, отношение длины окружности к диаметру одинаковое для всех кругов. Это отношение длины окружности к диаметру обозначается греческой буквой $ \ pi \ приблизительно 3,14 $. Таким образом, формула длины окружности$$ C = D \ times \ pi $$
или же$$ C = 2 \ times r \ times \ pi $$
Архимед [Хит, Т.L., it A History of Greek Mathematics, 2 vol., Oxford, 1921] дал приближение к $ \ pi $ с помощью $$ \ pi \ приблизительно \ frac {22} 7 = 3,142857142857 … $$
Метод определения площади круга: Площадь круга — это количество квадратных единиц внутри этого круга. Разделив круг на равные части, как показано на рисунке ниже, мы можем переставить части примерно в прямоугольник. Длина этот приблизительный прямоугольник равен половине окружности круга, $ r \ times \ pi $. Ширина этого примерного прямоугольника равна радиусу окружности $ r $.2) $ и т. Д.
Ширина этого примерного прямоугольника равна радиусу окружности $ r $.2) $ и т. Д.Работа с площадью и периметром круга с шагом показывает полное пошаговое вычисление для нахождения окружности и площади круга с длиной радиуса $ 8 \; in $ с использованием формул окружности и площади . Для любое другое значение длины радиуса круга, просто введите положительное действительное число и нажмите кнопку СОЗДАТЬ РАБОТУ. Учащиеся начальной школы могут использовать этот круговой калькулятор для создания работы, проверки результатов периметра и площади двумерных фигур или для эффективного выполнения домашних заданий.Они могут использовать эти методы для определения площади и длины частей круга.
Калькулятор окружности окружности + руководство (и формула для ее определения)
Объяснение вычисления окружности
Понимание того, что такое окружность окружности и как ее вычислить, имеет решающее значение при переходе на более высокий уровень математики.
 В этой статье вы узнаете ответы на следующие вопросы.
В этой статье вы узнаете ответы на следующие вопросы.- Какова длина окружности?
- Как можно рассчитать длину окружности?
Окружность круга — это расстояние по внешней стороне круга.Это как периметр других форм, например квадратов. Вы можете думать об этом как о линии, определяющей форму. Для форм, состоящих из прямых краев, эта линия называется периметром , но для окружностей эта определяющая линия называется окружностью .
На этой диаграмме показана длина окружности.
На окружности есть два других важных расстояния: радиус (r) и диаметр (d). Радиус, диаметр и длина окружности — три определяющих аспекта каждого круга.Зная радиус или диаметр и число пи, вы можете вычислить длину окружности. Диаметр — это расстояние от одной стороны круга до другой в самых широких точках. Диаметр всегда проходит через центр круга.
 Радиус составляет половину этого расстояния. Вы также можете думать о радиусе как о расстоянии между центром круга и его краем.
Радиус составляет половину этого расстояния. Вы также можете думать о радиусе как о расстоянии между центром круга и его краем.На этой диаграмме показаны окружность, диаметр, центр и радиус окружности.
Как можно рассчитать длину окружности?Если вы знаете диаметр или радиус окружности, вы можете вычислить длину окружности.Для начала вспомним, что пи — это иррациональное число, записываемое символом π. π примерно равно 3,14.
Формула для вычисления длины окружности:
Окружность окружности = π x Диаметр окружности
Обычно это записывается как C = πd. Это говорит нам о том, что длина окружности в три «с небольшим» раза больше диаметра. Мы можем видеть это на рисунке ниже:
Вы также можете вычислить длину окружности, если знаете ее радиус.Помните, что диаметр в два раза больше радиуса. Мы уже знаем, что C = πd. Если r — радиус окружности, то d = 2r. Итак, C = 2πr.
Пример 1Если круг имеет диаметр 10 см, какова его окружность?
ОтветМы знаем, что C = πd.
Пример 2 Поскольку диаметр равен 10 см, мы знаем, что C = π x 10 см = 31,42 см (с точностью до 2 знаков после запятой).
Поскольку диаметр равен 10 см, мы знаем, что C = π x 10 см = 31,42 см (с точностью до 2 знаков после запятой).Если круг имеет радиус 3 м, какова его длина?
ОтветМы знаем, что C = 2πr.Поскольку радиус равен 3 м, мы знаем, что C = π x 6m = C = 18,84 м (с точностью до 2 знаков после запятой).
Пример 3Найдите недостающую длину (отмеченную знаком?) На диаграмме ниже:
ОтветНедостающая длина — это длина окружности. Зная, что диаметр на диаграмме составляет 4,3 м, и зная, что C = πd, мы можем вычислить длину окружности. Немного подумав, мы можем легко понять, что C = π x 4,3 м = 13,51 м (с точностью до 2 знаков после запятой).Недостающая длина 13,51 м.
Как рассчитать длину окружности ЗемлиВы когда-нибудь задумывались, насколько велика Земля? Что ж, с помощью числа Пи можно вычислить окружность Земли! Ученые обнаружили, что диаметр Земли составляет 12742 км.
 bani-nsk.ru - Дома и бани из бруса - Под ключ в Новосибирске © 2025 Карта сайта
bani-nsk.ru - Дома и бани из бруса - Под ключ в Новосибирске © 2025 Карта сайта





 Для теплоизоляции понадобится материал большей площади, так как обычно трубы заворачиваются в минеральную вату с перехлестом полотен.
Для теплоизоляции понадобится материал большей площади, так как обычно трубы заворачиваются в минеральную вату с перехлестом полотен. Основные сферы применения – очистные сооружения канализации и открытые дождевые сети.
Основные сферы применения – очистные сооружения канализации и открытые дождевые сети.
 В данном случае сам процесс называют расчет трубы, а включает он в себя как измерения, так и вычисления.
В данном случае сам процесс называют расчет трубы, а включает он в себя как измерения, так и вычисления.  Используют их чаще для строительства заборов, каркасов для хозпостроек (гаражей, сараев, беседок, бытовок), так что условия эксплуатации — тяжелы, защита необходима, потому все каркасы требуют окраски. Вот тут и потребуется площадь окрашиваемой поверхности — наружная площадь трубы.
Используют их чаще для строительства заборов, каркасов для хозпостроек (гаражей, сараев, беседок, бытовок), так что условия эксплуатации — тяжелы, защита необходима, потому все каркасы требуют окраски. Вот тут и потребуется площадь окрашиваемой поверхности — наружная площадь трубы. Они имеют внутренний и наружный диаметр, так как стенка у них толстая, ее толщина зависит от типа трубы и материала из которого она изготовлена. В технических характеристиках чаще указывают наружный диаметр и толщину стенки.
Они имеют внутренний и наружный диаметр, так как стенка у них толстая, ее толщина зависит от типа трубы и материала из которого она изготовлена. В технических характеристиках чаще указывают наружный диаметр и толщину стенки.
 Если округлить, получится 1,9 м2.
Если округлить, получится 1,9 м2.
 Рассчитаем сколько воды поместится в системе из 32 миллиметровых труб длиной 30 метров.
Рассчитаем сколько воды поместится в системе из 32 миллиметровых труб длиной 30 метров. 2*L.
2*L. За 1″ согласно общепринятым меркам принимают 25,4 миллиметра. На сегодняшний день стальные трубы можно встретить в усиленном (с двойной стенкой) или в обычном исполнении.
За 1″ согласно общепринятым меркам принимают 25,4 миллиметра. На сегодняшний день стальные трубы можно встретить в усиленном (с двойной стенкой) или в обычном исполнении.

 ) производится на основе имеющихся в справочниках ГОСТ и ТУ данных. Вес метра трубы, сортамент которой не входит в имеющиеся на сайте справочники, рассчитывается онлайн по формуле m = Pi * ro * S * (D — S) * L; Pi — математическая константа, которая выражает отношение длины окружности к её диаметру, равная ~3.14; ro — плотность металла из которой изготовлена круглая труба в кг/м³; Для расчета удельного веса 1 погонного метра трубы (m) необходимо указать размеры профиля трубы: диаметр D в мм, а также толщину металла, из которого изготовлена труба (толщину стенки S) и длину L (по умолчанию 1 м). Расчет теоретического веса прямоугольной профильной трубы производится аналогично круглой, за исключением части формулы для определения площади поперечного сечения.
) производится на основе имеющихся в справочниках ГОСТ и ТУ данных. Вес метра трубы, сортамент которой не входит в имеющиеся на сайте справочники, рассчитывается онлайн по формуле m = Pi * ro * S * (D — S) * L; Pi — математическая константа, которая выражает отношение длины окружности к её диаметру, равная ~3.14; ro — плотность металла из которой изготовлена круглая труба в кг/м³; Для расчета удельного веса 1 погонного метра трубы (m) необходимо указать размеры профиля трубы: диаметр D в мм, а также толщину металла, из которого изготовлена труба (толщину стенки S) и длину L (по умолчанию 1 м). Расчет теоретического веса прямоугольной профильной трубы производится аналогично круглой, за исключением части формулы для определения площади поперечного сечения.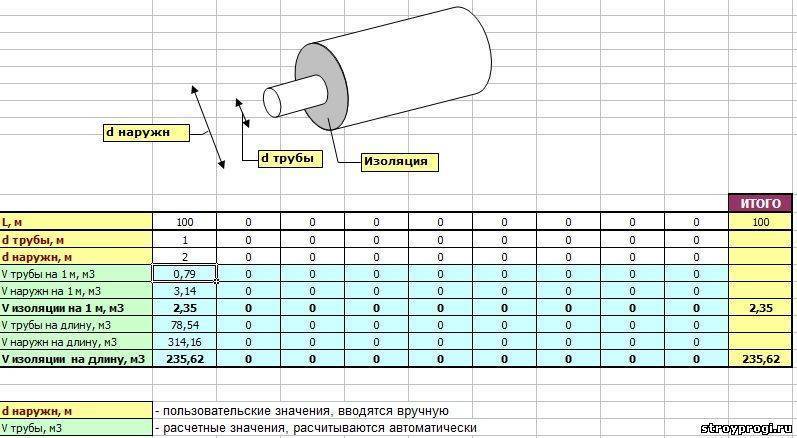 Холоднодеформированные
Холоднодеформированные
 Так, S=Пи*R*R, где R — радиус трубы. Площадь сечения будет найдена в той же системе единиц, в которой было взято значение радиуса. Например, если значение радиуса представлено в сантиметрах, то площадь сечения будет вычислена в квадратных сантиметрах.
Так, S=Пи*R*R, где R — радиус трубы. Площадь сечения будет найдена в той же системе единиц, в которой было взято значение радиуса. Например, если значение радиуса представлено в сантиметрах, то площадь сечения будет вычислена в квадратных сантиметрах.
 Все объекты, рассматриваемые в этом калькуляторе, более подробно описаны на страницах «Калькулятор объема» и «Калькулятор площади». Таким образом, этот калькулятор будет сосредоточен на уравнениях для расчета площади поверхности объектов и использовании этих уравнений. Пожалуйста, обратитесь к вышеупомянутым калькуляторам для получения более подробной информации по каждому отдельному объекту.
Все объекты, рассматриваемые в этом калькуляторе, более подробно описаны на страницах «Калькулятор объема» и «Калькулятор площади». Таким образом, этот калькулятор будет сосредоточен на уравнениях для расчета площади поверхности объектов и использовании этих уравнений. Пожалуйста, обратитесь к вышеупомянутым калькуляторам для получения более подробной информации по каждому отдельному объекту.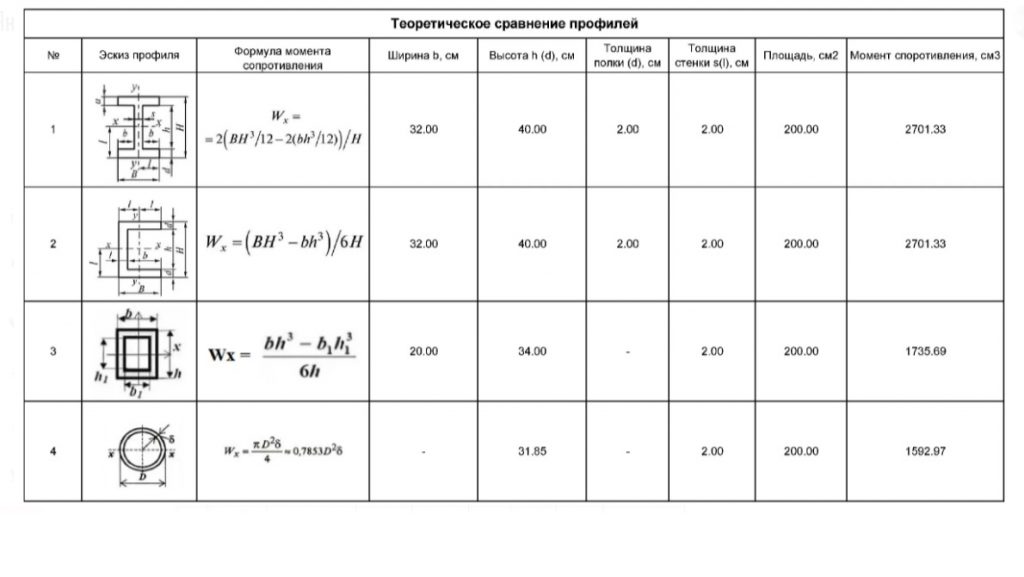 «Базовая SA» относится к кругу, который содержит основание в замкнутом круговом конусе, в то время как боковая SA относится к остальной части конуса между основанием и его вершиной. Уравнения для расчета каждого из них, а также общая SA замкнутого кругового конуса показаны ниже:
«Базовая SA» относится к кругу, который содержит основание в замкнутом круговом конусе, в то время как боковая SA относится к остальной части конуса между основанием и его вершиной. Уравнения для расчета каждого из них, а также общая SA замкнутого кругового конуса показаны ниже: Она заказывает кубик Рубика, у которого все грани черные, и должна платить за настройку в зависимости от площади поверхности куба с длиной ребра 4 дюйма.
Она заказывает кубик Рубика, у которого все грани черные, и должна платить за настройку в зависимости от площади поверхности куба с длиной ребра 4 дюйма.
 Общая площадь рассчитывается следующим образом:
Общая площадь рассчитывается следующим образом: Предоставленный калькулятор предполагает твердую сферу и включает основание крышки при расчете площади поверхности, где общая площадь поверхности является суммой площади основания и боковой поверхности сферической крышки.Если вы используете этот калькулятор для вычисления площади поверхности полой сферы, вычтите площадь поверхности основания. Учитывая два значения высоты, радиуса крышки или радиуса основания, третье значение можно рассчитать с помощью уравнений, представленных в Калькуляторе объема. Уравнения площади поверхности следующие:
Предоставленный калькулятор предполагает твердую сферу и включает основание крышки при расчете площади поверхности, где общая площадь поверхности является суммой площади основания и боковой поверхности сферической крышки.Если вы используете этот калькулятор для вычисления площади поверхности полой сферы, вычтите площадь поверхности основания. Учитывая два значения высоты, радиуса крышки или радиуса основания, третье значение можно рассчитать с помощью уравнений, представленных в Калькуляторе объема. Уравнения площади поверхности следующие: Вернув ручную пилу своего отца в сарай для инструментов, она вычисляет площадь поверхности своей полой части земного шара с R 0,80 фута и h 0,53 фута, как показано ниже:
Вернув ручную пилу своего отца в сарай для инструментов, она вычисляет площадь поверхности своей полой части земного шара с R 0,80 фута и h 0,53 фута, как показано ниже: Хотя его вулкан вряд ли произведет впечатление на судей научной ярмарки, Пол все же должен определить площадь поверхности материала, которую ему нужно покрыть внешнюю стену своего вулкана с R на 1 фут, на на 0,3 фута и на . 1,5 фута:
Хотя его вулкан вряд ли произведет впечатление на судей научной ярмарки, Пол все же должен определить площадь поверхности материала, которую ему нужно покрыть внешнюю стену своего вулкана с R на 1 фут, на на 0,3 фута и на . 1,5 фута: К несчастью для своей семьи, которая почти полностью ест мясо, Колтейн практиковал свою технику нарезки чрезмерного количества овощей. Вместо того, чтобы есть овощи, отец Колтейна уныло смотрит на свою тарелку и оценивает площадь поверхности эллиптических разрезов кабачков с помощью топоров 0,1, 0,2 и 0,35 дюйма:
К несчастью для своей семьи, которая почти полностью ест мясо, Колтейн практиковал свою технику нарезки чрезмерного количества овощей. Вместо того, чтобы есть овощи, отец Колтейна уныло смотрит на свою тарелку и оценивает площадь поверхности эллиптических разрезов кабачков с помощью топоров 0,1, 0,2 и 0,35 дюйма: Тем не менее, она считает, что модель не излучает того архитектурного чуда, как оригинал, и решает, что покрытие ее «снегом», по крайней мере, придаст вид чуда. Она вычисляет площадь поверхности расплавленного сахара, которая потребуется ей, чтобы полностью покрыть пирамиду, с длиной ребра a 3 фута и высотой h 5 футов:
Тем не менее, она считает, что модель не излучает того архитектурного чуда, как оригинал, и решает, что покрытие ее «снегом», по крайней мере, придаст вид чуда. Она вычисляет площадь поверхности расплавленного сахара, которая потребуется ей, чтобы полностью покрыть пирамиду, с длиной ребра a 3 фута и высотой h 5 футов: 83613
83613

 Однако вместо того, чтобы делать что-то вручную, теперь вы можете использовать наш калькулятор площади круга и формулу готового круга.
Однако вместо того, чтобы делать что-то вручную, теперь вы можете использовать наш калькулятор площади круга и формулу готового круга.
 7639, чтобы получить футов 2
7639, чтобы получить футов 2  Этот калькулятор — полезный инструмент для всех, кому нужно знать точный объем воды в трубе. Вам будет полезно, например, если вы проектируете систему полива для своего сада. Продолжайте читать, чтобы узнать, что такое цилиндр, найдите формулу объема трубы и проверьте «руководство пользователя» для правильных расчетов в калькуляторе объема трубы.
Этот калькулятор — полезный инструмент для всех, кому нужно знать точный объем воды в трубе. Вам будет полезно, например, если вы проектируете систему полива для своего сада. Продолжайте читать, чтобы узнать, что такое цилиндр, найдите формулу объема трубы и проверьте «руководство пользователя» для правильных расчетов в калькуляторе объема трубы. Неважно, используете ли вы метрическую или британскую систему единиц, потому что вы можете свободно переключаться между ними с помощью раскрывающегося списка.
Неважно, используете ли вы метрическую или британскую систему единиц, потому что вы можете свободно переключаться между ними с помощью раскрывающегося списка. Итак, для расчетов нужно диаметр уменьшить вдвое.
Итак, для расчетов нужно диаметр уменьшить вдвое.

 7854 d i 2 (6)
7854 d i 2 (6)  Радиус круга должен быть положительным вещественным числом. Окружность с центром $ O $ и радиусом $ r $ обозначается $ c (O, r) $.
Радиус круга должен быть положительным вещественным числом. Окружность с центром $ O $ и радиусом $ r $ обозначается $ c (O, r) $.  Этот предел — окружность. Следовательно, окружность окружности — это предел периметра правильного многоугольника, вписанного в окружность, когда число его вершин бесконечно удваивается. Поскольку все круги похожи, отношение длины окружности к диаметру одинаковое для всех кругов. Это отношение длины окружности к диаметру обозначается греческой буквой $ \ pi \ приблизительно 3,14 $. Таким образом, формула длины окружности
Этот предел — окружность. Следовательно, окружность окружности — это предел периметра правильного многоугольника, вписанного в окружность, когда число его вершин бесконечно удваивается. Поскольку все круги похожи, отношение длины окружности к диаметру одинаковое для всех кругов. Это отношение длины окружности к диаметру обозначается греческой буквой $ \ pi \ приблизительно 3,14 $. Таким образом, формула длины окружности Ширина этого примерного прямоугольника равна радиусу окружности $ r $.2) $ и т. Д.
Ширина этого примерного прямоугольника равна радиусу окружности $ r $.2) $ и т. Д.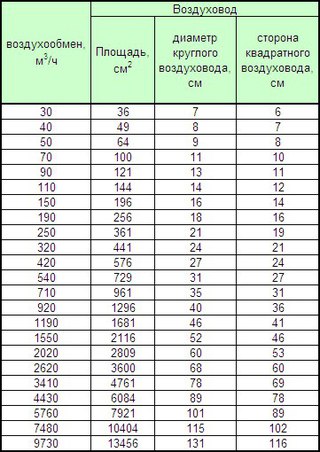 В этой статье вы узнаете ответы на следующие вопросы.
В этой статье вы узнаете ответы на следующие вопросы. Радиус составляет половину этого расстояния. Вы также можете думать о радиусе как о расстоянии между центром круга и его краем.
Радиус составляет половину этого расстояния. Вы также можете думать о радиусе как о расстоянии между центром круга и его краем. Поскольку диаметр равен 10 см, мы знаем, что C = π x 10 см = 31,42 см (с точностью до 2 знаков после запятой).
Поскольку диаметр равен 10 см, мы знаем, что C = π x 10 см = 31,42 см (с точностью до 2 знаков после запятой).