Формула массы цилиндра: Расчет массы цилиндра

Содержание

Расчет массы цилиндра — однородного и полого

Цилиндр является одной из простых объемных фигур, которую изучают в школьном курсе геометрии (раздел стереометрия). При этом часто возникают задачи на расчет объема и массы цилиндра, а также на определение площади его поверхности. Ответы на отмеченные вопросы даны в этой статье.

Что такое цилиндр?

Перед тем как переходить к ответу на вопрос, чему равна масса цилиндра и его объем, стоит рассмотреть, что представляет собой эта пространственная фигура. Сразу необходимо отметить, что цилиндр — это трехмерный объект. То есть в пространстве можно измерить три его параметра по каждой из осей в декартовой прямоугольной системе координат. В действительности для однозначного определения размеров цилиндра достаточно знать всего два его параметра.

Цилиндр — это объемная фигура, образованная двумя кругами и цилиндрической поверхностью. Чтобы яснее представить этот объект, достаточно взять прямоугольник и начать вращать его вокруг какой-либо его стороны, которая будет осью вращения. В этом случае вращающийся прямоугольник опишет фигуру вращения — цилиндр.

Две круглые поверхности называются основаниями цилиндра, они характеризуются определенным радиусом. Расстояние между основаниями называется высотой. Два основания соединены между собой цилиндрической поверхностью. Линия, проходящая через центры обоих кругов, называется осью цилиндра.

Объем и площадь поверхности

Как можно заметить из вышесказанного, цилиндр определяется двумя параметрами: высотой h и радиусом его основания r. Зная эти параметры, можно рассчитать все другие характеристики рассматриваемого тела. Ниже приводятся основные из них:

Площадь оснований. Эта величина рассчитывается по формуле: S₁ = 2*pi*r², где pi — число пи, равное 3,14. Цифра 2 в формуле появляется потому, что цилиндр имеет два одинаковых основания.
Площадь цилиндрической поверхности. Ее можно рассчитать так: S₂ = 2*pi*r*h. Понять эту формулу просто: если цилиндрическую поверхность разрезать вертикально от одного основания к другому и развернуть, то получится прямоугольник, высота которого будет равна высоте цилиндра, а ширина будет соответствовать длине окружности основания объемной фигуры. Поскольку площадь полученного прямоугольника — это произведение его сторон, которые равны h и 2*pi*r, то получается представленная выше формула.
Площадь поверхности цилиндра. Она равна сумме площадей S₁ и S₂, получаем: S₃ = S₁ + S₂ = 2*pi*r² + 2*pi*r*h = 2*pi*r*(r+h).
Объем. Эта величина находится просто, необходимо лишь умножить площадь одного основания на высоту фигуры: V = (S₁/2)*h = pi*r²*h.

Определение массы цилиндра

Наконец, стоит перейти непосредственно к теме статьи. Как определить массу цилиндра? Для этого необходимо знать его объем, формула для вычисления которого была представлена выше. И плотность вещества, из которого он состоит. Масса определяется по простой формуле: m = ρ*V, где ρ — плотность материала, образующего рассматриваемый объект.

Понятие плотности характеризует массу вещества, которое находится в единице объема пространства. Например. Известно, что железо имеет большую плотность, чем дерево. Это означает, что в случае одинаковых объемов вещества железа и дерева первое будет иметь намного большую массу, чем второе (приблизительно в 16 раз).

Расчет массы медного цилиндра

Рассмотрим простую задачу. Необходимо найти массу цилиндра, сделанного из меди. Для определенности пусть цилиндр имеет диаметр 20 см и высоту 10 см.

Перед тем как приступать к решению задачи, следует разобраться с исходными данными. Радиус цилиндра равен половине его диаметра, значит r = 20/2 = 10 см, высота же составляет h = 10 см. Поскольку рассматриваемый в задаче цилиндр сделан из меди, то, обращаясь к справочным данным, выписываем значение плотности этого материала: ρ = 8,96 г/см³ (для температуры 20 °C).

Теперь можно приступать к решению задачи. Для начала рассчитаем объем: V =pi*r²*h = 3,14*(10)²*10 = 3140 см³. Тогда масса цилиндра будет равна: m = ρ*V = 8,96 * 3140 = 28134 грамм или приблизительно 28 килограмм.

Следует обратить внимание на размерность единиц во время их использования в соответствующих формулах. Так, в задаче все параметры были представлены в сантиметрах и граммах.

Однородный и полый цилиндры

Из полученного выше результата можно видеть, что медный цилиндр с относительно малыми размерами (10 см) обладает большой массой (28 кг). Это связано не только с тем, что он сделан из тяжелого материала, но и с тем, что он является однородным. Этот факт важно понимать, поскольку приведенную выше формулу для расчета массы можно использовать только в случае, если цилиндр полностью (снаружи и внутри) состоит из одного и того же материала, то есть является однородным.

На практике же часто используют полые цилиндры (например, цилиндрические бочки для воды). То есть они сделаны из тонких листов какого-то материала, а внутри являются пустыми. Для полого цилиндра указанной формулой расчета массы пользоваться нельзя.

Интересно рассчитать, какой массой будет обладать цилиндр из меди, если он является пустым внутри. Для примера пусть он будет сделан из тонкого медного листа толщиной всего d = 2 мм.

Чтобы решить эту задачу, нужно найти объем самой меди, из которой сделан объект. А не объем цилиндра. Поскольку толщина листа мала, по сравнению с размерами цилиндра (d = 2 мм и r = 10 см), тогда объем меди, из которой изготовлен предмет, можно найти, если умножить всю площадь поверхности цилиндра на толщину медного листа, получаем: V = d*S₃ = d*2*pi*r*(r+h). Подставляя данные из предыдущей задачи, получим: V = 0,2*2*3,14*10*(10+10) = 251,2 см³. Массу полого цилиндра можно получить, если умножить полученный объем меди, который потребовался для его изготовления, на плотность меди: m = 251,2 * 8,96 = 2251 г или 2,3 кг. То есть рассмотренный полый цилиндр весит в 12 (28,1/2,3) раз меньше, чем однородный.

Масса сплошной детали | Математика для ювелиров

9.05.2013 // Владимир Трунов

Это странное название статьи объясняется только тем, что детали одной и той же формы могут быть как сплошными, так и полыми (т.е. следующая статья будет называться «Масса полой детали»).

Тут самое время вспомнить, что масса тела — это его объем , умноженный на плотность его материала rho (см. таблицы плотностей):

Объем сплошной детали — это… ее объем и больше ничего.

Примечание. В приведенных ниже формулах все размеры измеряются в миллиметрах, а плотность — в граммах на кубический сантиметр.

Буквой обозначено отношение длины окружности к ее диаметру, составляющее примерно 3,14.

Рассмотрим несколько простых форм (более сложные, как вы помните, можно составить путем сложения или вычитания простых).

1. Масса параллелепипеда (бруска)

Объем параллелепипеда:

, где

— длина,

— ширина,

— высота.
Тогда масса:

2. Масса цилиндра

Объем цилиндра: $V~=~pi~*~{D^2/4}~*~H$ , где

— диаметр основания,

— высота цилиндра.
Тогда масса:

$m~=~{{pi~*~D^2~*~H}/4000}~*~rho$

3. Масса шара

шар Объем шара: $V~=~pi~*~{D^3/6}$ , где — диаметр шара.
Тогда масса:

$m~=~{{pi~*~D^3}/6000}~*~rho$

4. Масса сегмента шара

Объем сегмента шара: $V~=~{1/6}pi*H*(H^2+~{3/4}D^2)$ , где — диаметр основания сегмента, — высота сегмента.
Тогда масса:

$m~=~{{pi~*~H~*~(4H^2+~3D^2)}/24000}~*~rho$

5. Масса конуса

Объем любого конуса: , где — площадь основания, — высота конуса.
Для круглого конуса: $V~=~{1/12}pi*D^2*H$ , где — диаметр основания, — высота конуса.
Масса круглого конуса:

$m~=~{{pi~*~D^2~*~H}/12000}~*~rho$

6. Масса усеченного конуса

Поскольку невозможно объять необъятное, рассмотрим только круглый усеченный конус. Его объем — это разность объемов двух вложенных конусов: с основаниями и : $V~=~{1/12}pi*(D1^2*h2~-~D2^2*h3)$ , где , . После никому не интересных алгебраических преобразований получаем:
$V~=~{1/12}pi*H*(D1^2+D1*D2+D2^2)$ , где — диаметр большего основания, — диаметр меньшего основания, — высота усеченного конуса.
Отсюда масса:

$m~=~{{pi~*~H~*~(D1^2~+~D1*D2~+~D2^2)}/12000}~*~rho$

7. Масса пирамиды

Объем любой пирамиды равен одной трети произведения площади ее основания на высоту (то же самое, что и для конусов (часто мы не замечаем, насколько мироздание к нам благосклонно)): , где — площадь основания, — высота пирамиды.
Для пирамиды с прямоугольным основанием: , где — ширина, — длина, — высота пирамиды.
Тогда масса пирамиды:

8. Масса усеченной пирамиды

Рассмотрим усеченную пирамиду с прямоугольным основанием. Ее объем — это разность объемов двух подобных пирамид с основаниями W1*L1 и W2*L2 : , где , .
Исчеркав половину тетрадного листа, получаем: $V~=~{1/3}H*~{{W1^2L1~-~W2^2L2}/{W1~-~W2}}$ , где , — ширина и длина большего основания, , — ширина и длина меньшего основания, — высота пирамиды.
И, оставив в покое остальную половину листа, исходя из одних соображений симметрии, мы можем написать еще одну формулу, которая отличается от предыдущей только заменой W на L и наоборот. В чем разница между длиной и шириной? Только в том, что мы их так назвали. Назовем наоборот и получим: $V~=~{1/3}H*~{{L1^2W1~-~L2^2W2}/{L1~-~L2}}$ .
Тогда масса усеченной прямоугольной пирамиды:

$m~=~{{W1^2L1~-~W2^2L2}/{W1~-~W2}}~*~{H~*~rho}/3000$

или

$m~=~{{L1^2W1~-~L2^2W2}/{L1~-~L2}}~*~{H~*~rho}/3000$

Для пирамиды с квадратным основанием (, ) формула выглядит проще:

$m~=~(A1^2~+~A1A2~+~A2^2)~*~{H~*~rho}/3000$

Калькулятор массы

Плотность материалов
Наименование	Плотность ρ, кг/м3
Черные металлы
Сталь 10 ГОСТ 1050-88	7856
Сталь 20 ГОСТ 1050-88	7859
Сталь 40 ГОСТ 1050-88	7850
Сталь 60 ГОСТ 1050-88	7800
С235-С375 ГОСТ 27772-88	7850
Ст3пс ГОСТ 380-2005	7850
Чугун ковкий КЧ 70-2 ГОСТ 1215-79	7000
Чугун высокопрочный ВЧ35 ГОСТ 7293-85	7200
Чугун серый СЧ10 ГОСТ 1412-85	6800
Чугун серый СЧ20 ГОСТ 1412-85	7100
Чугун серый СЧ30 ГОСТ 1412-85	7300
Алюминий и сплавы алюминиевые
Силумин АК12ж ГОСТ 1583-93	2700
Сплав АК12 ГОСТ 1583-93	2710
Сплав АК5М ГОСТ 1583-93	2640
Сплав АК7 ГОСТ 1583-93	2700
Сплав АО9-1 ГОСТ 14113-78	2700
Магний и сплавы магниевые
Сплав ВМЛ9	1850
Сплав ВМЛ5	1890
Сплав МЛ10…МЛ19 ГОСТ 2856-79	1810
Баббиты оловянные и свинцовые
Б83 ГОСТ 1320-74	7380
Б87 ГОСТ 1320-74	7300
БН ГОСТ 1320-74	9550
Медь и медные сплавы
Бронза оловянная БрО10C10	8800
Бронза оловянная БрО19	8600
Бронза оловянная БрОC10-10	9100
Бронза оловянная БрОA10-1	8750
Бронза БрА10Ж3Мч2 ГОСТ 493-79	8200
Бронза БрА9Ж3Л ГОСТ 493-79	8200
Бронза БрМц5 ГОСТ 18175-78	8600
Латунь Л60 ГОСТ 15527-2004	8800
Латунь ЛА ГОСТ 1020-97	8500
Медь М0, М1, М2, М3 ГОСТ 859-2001	8940
Медь МСр1 ГОСТ 16130-90	8900
Титан и титановые сплавы
ВТ1-0 ГОСТ 19807-91	4500
ВТ14 ГОСТ 19807-91	4500
ВТ20Л ГОСТ 19807-91	4470
Фторопласты
Ф-4 ГОСТ 10007-80 Е	2100
Фторопласт — 1 ГОСТ 13744-87	1400
Фторопласт — 2 ГОСТ 13744-87	1700
Фторопласт — 3 ГОСТ 13744-87	2710
Фторопласт — 4Д ГОСТ 14906-77	2150
Термопласты
Дакрил-2М ТУ 2216-265-057 57 593-2000	1190
Полиметилметакрилат ЛПТ ТУ 6-05-952-74	1180
Полиметилметакрилат суспензионный ЛСОМ ОСТ 6-01-67-72	1190
Винипласт УВ-10 ТУ 6-01-737-72	1450
Поливинилхлоридный пластикат ГОСТ 5960-72	1400
Полиамид ПА6 блочный Б ТУ 6-05-988-87	1150
Полиамид ПА66 литьевой ОСТ 6-06-369-74	1140
Капролон В ТУ 6-05-988	1150
Капролон ТУ 6-06-309-70	1130
Поликарбонат	1200
Полипропилен ГОСТ 26996-86	900
Полиэтилен СД	960
Лавсан литьевой ТУ 6-05-830-76	1320
Лавсан ЛС-1 ТУ 6-05-830-76	1530
Стиролпласт АБС 0809Т ТУ 2214-019-002 03521-96	1050
Полистирол блочный ГОСТ 20282-86	1050
Сополимер стирола МСН ГОСТ 12271-76	1060
Полистирол ударопрочный УПС-0505 ГОСТ 28250-89	1060
Стеклопластик ВПС-8	1900
Стеклотекстолит конструкционный КАСТ-В ГОСТ 10292-74	1850
Винилискожа-НТ ГОСТ 10438-78	1440
Резина 6Ж ТУ 38-005-1166-98	1050
Резина ВР-10 ТР 18-962	1800
Стекло листовое ГОСТ 111-2001	2500
Стекло органическое техническое ТОСН ГОСТ 17622-72	1180
Прочие металлы
Вольфрам ВА ГОСТ 18903-73	19300
Вольфрам ВТ-7 ГОСТ 18903-73	19300
Золото Зл 99,9 ГОСТ 6835-2002	19300
Индий ИНО ГОСТ 10297-94	7300
Кадмий КдО ГОСТ 1467-93	8640
Олово О1пч ГОСТ 860-75	7300
Паладий Пд 99,8 ГОСТ 13462-79	12160
Платина Пд 99,8 ГОСТ 13498-79	21450
Свинец С0 ГОСТ 3778-98	11400
Серебро 99,9 ГОСТ 6836-2002	11500
Цинк Ц1 ГОСТ 3640-94	7130
Прочие материалы
Древесина, пробка	480
Древесина, лиственница	660
Древесина, липа	530
Древесина, ель	450
Древесина, сосна	520
Древесина, береза	650
Древесина, бук	690
Бумага	700-1200
Резина	900-2000
Кирпич	1400-2100
Фарфор	2300
Бетон	2000-2200
Цемент	2800-3000

Расчет массы цилиндра — однородного и полого — OneKu

Содержание статьи:

Что такое цилиндр?

Вам будет интересно:Хоперские казаки: история возникновения, нагрудные и нарукавные знаки, фото

Объем и площадь поверхности

Площадь оснований. Эта величина рассчитывается по формуле: S1 = 2*pi*r2, где pi — число пи, равное 3,14. Цифра 2 в формуле появляется потому, что цилиндр имеет два одинаковых основания.
Площадь цилиндрической поверхности. Ее можно рассчитать так: S2 = 2*pi*r*h. Понять эту формулу просто: если цилиндрическую поверхность разрезать вертикально от одного основания к другому и развернуть, то получится прямоугольник, высота которого будет равна высоте цилиндра, а ширина будет соответствовать длине окружности основания объемной фигуры. Поскольку площадь полученного прямоугольника — это произведение его сторон, которые равны h и 2*pi*r, то получается представленная выше формула.

Площадь поверхности цилиндра. Она равна сумме площадей S1 и S2, получаем: S3 = S1 + S2 = 2*pi*r2 + 2*pi*r*h = 2*pi*r*(r+h).
Объем. Эта величина находится просто, необходимо лишь умножить площадь одного основания на высоту фигуры: V = (S1/2)*h = pi*r2*h.

Определение массы цилиндра

Расчет массы медного цилиндра

Теперь можно приступать к решению задачи. Для начала рассчитаем объем: V =pi*r2*h = 3,14*(10)2*10 = 3140 см3. Тогда масса цилиндра будет равна: m = ρ*V = 8,96 * 3140 = 28134 грамм или приблизительно 28 килограмм.

Однородный и полый цилиндры

Расчет массы полого цилиндра

Чтобы решить эту задачу, нужно найти объем самой меди, из которой сделан объект. А не объем цилиндра. Поскольку толщина листа мала, по сравнению с размерами цилиндра (d = 2 мм и r = 10 см), тогда объем меди, из которой изготовлен предмет, можно найти, если умножить всю площадь поверхности цилиндра на толщину медного листа, получаем: V = d*S3 = d*2*pi*r*(r+h). Подставляя данные из предыдущей задачи, получим: V = 0,2*2*3,14*10*(10+10) = 251,2 см3. Массу полого цилиндра можно получить, если умножить полученный объем меди, который потребовался для его изготовления, на плотность меди: m = 251,2 * 8,96 = 2251 г или 2,3 кг. То есть рассмотренный полый цилиндр весит в 12 (28,1/2,3) раз меньше, чем однородный.

Источник

Масса полой детали | Математика для ювелиров

1.06.2013 // Владимир Трунов

Никогда не устану повторять, что масса тела — это его объем , умноженный на плотность его материала rho (см. таблицы плотностей):

Однако, в случае полой или пустотелой детали мы будем иметь дело не с объемом ее тела, а с объемом ее стенок. Объем стенок полой детали проще всего представить как разность объемов двух сплошных тел: с внешними размерами и с внутренними (из полного объема тела вычитается объем внутренней пустоты).
Формулы для объема сплошных тел можно найти в статье «Масса сплошной детали».

Примечание. В приведенных ниже формулах все размеры измеряются в миллиметрах, а плотность — в граммах на кубический сантиметр.
Буквой обозначено отношение длины окружности к ее диаметру, составляющее примерно 3,14.

1. Масса трубки (полого цилиндра)

Объем стенок трубки: $V~=~{pi{D^2/4}L}~-~{pi{(D~-~2T)^2/4}L}$ , где — внешний диаметр трубки, — длина трубки, — толщина стенки.
После упрощения получаем формулу для объема:
Тогда масса трубки:

2. Масса полого (пустотелого) шара

шар Объем стенок шара: $V~=~{pi/6}*(D^3~-~(D~-~2T)^3)$ , где — внешний диаметр шара, — толщина стенки.
Тогда масса:

$m~=~pi~*~{{D^3~-~(D~-~2T)^3}/6000}~*~rho$

3. Масса полого сегмента шара

Объем стенок сегмента шара: $V={pi/6}H((H^2+{3/4}D^2)~-~((H-T)^2+{3/4}(D-2T)^2))$ , где — внешний диаметр основания сегмента, — высота сегмента, — толщина стенки*.
После упрощения получаем формулу для объема:
Тогда масса:

m~=~{{pi~*~H~*~T~*~(H~+~3D~-~4T)}/6000}~*~rho

4. Масса полого усеченного конуса

Объем стенок круглого усеченного конуса: $V={pi/12}H(D1^2+D1*D2+D2^2-(D1-2T)^2-(D1-2T)(D2-2T)-(D2-2T)^2)$ , где — внешний диаметр большего основания, — внешний диаметр меньшего основания, — высота конуса, — толщина стенки*.
После упрощения получаем формулу для объема:
Тогда масса:

m~=~{{pi~*~H~*~T~*~(D1~+~D2~-~2T)}/2000}~*~rho

5. Масса полой усеченной пирамиды

Для простоты рассмотрим усеченную пирамиду с квадратным основанием. Объем ее стенок: $V={H/3}(A1^2+A1*A2+A2^2-(A1-2T)^2-(A1-2T)(A2-2T)-(A2-2T)^2)$ , где — внешний размер большего основания, — внешний размер меньшего основания, — высота пирамиды, — толщина стенки*.
После упрощения получаем формулу для объема:
Тогда масса:

m~=~{{H~*~T~*~(A1~+~A2~-~2T)}/3000}~*~rho

* в данном случае — это не вполне толщина стенки. Строго говоря, мы имеем тут дело с двумя величинами: та , что стоит в формулах за скобкой, это точно толщина стенки, а та , которую мы отнимаем от внешнего размера тела, чтобы получить его внутренний размер, — это толщина стенки, деленная на косинус угла наклона образующей. Но в большинстве случаев толщина стенки не превышает нескольких процентов от размеров тела, и ошибкой можно пренебречь. Однако, для толстостенных деталей это обстоятельство нужно учитывать.

Расчет массы однородного и полого цилиндров

Объем и площадь поверхности

Площадь оснований. Эта величина рассчитывается по формуле: S₁ = 2*pi*r², где pi — число пи, равное 3,14. Цифра 2 в формуле появляется потому, что цилиндр имеет два одинаковых основания.
Площадь цилиндрической поверхности. Ее можно рассчитать так: S₂ = 2*pi*r*h. Понять эту формулу просто: если цилиндрическую поверхность разрезать вертикально от одного основания к другому и развернуть, то получится прямоугольник, высота которого будет равна высоте цилиндра, а ширина будет соответствовать длине окружности основания объемной фигуры. Поскольку площадь полученного прямоугольника — это произведение его сторон, которые равны h и 2*pi*r, то получается представленная выше формула.
Площадь поверхности цилиндра. Она равна сумме площадей S₁ и S₂, получаем: S₃ = S₁ + S₂ = 2*pi*r² + 2*pi*r*h = 2*pi*r*(r+h).
Объем. Эта величина находится просто, необходимо лишь умножить площадь одного основания на высоту фигуры: V = (S₁/2)*h = pi*r²*h.

Определение массы цилиндра

Расчет массы медного цилиндра

Теперь можно приступать к решению задачи. Для начала рассчитаем объем: V =pi*r²*h = 3,1 (10)²*10 = 3140 см³. Тогда масса цилиндра будет равна: m = ρ*V = 8,96 * 3140 = 28134 грамм или приблизительно 28 килограмм.

Однородный и полый цилиндры

Расчет массы полого цилиндра

Чтобы решить эту задачу, нужно найти объем самой меди, из которой сделан объект. А не объем цилиндра. Поскольку толщина листа мала, по сравнению с размерами цилиндра (d = 2 мм и r = 10 см), тогда объем меди, из которой изготовлен предмет, можно найти, если умножить всю площадь поверхности цилиндра на толщину медного листа, получаем: V = d*S₃ = d*2*pi*r*(r+h). Подставляя данные из предыдущей задачи, получим: V = 0,2*2*3,1 10*(10+10) = 251,2 см³. Массу полого цилиндра можно получить, если умножить полученный объем меди, который потребовался для его изготовления, на плотность меди: m = 251,2 * 8,96 = 2251 г или 2,3 кг. То есть рассмотренный полый цилиндр весит в 12 (28,1/2,3) раз меньше, чем однородный.

Введение к вычислению масс | Математика для ювелиров

4.05.2013 // Владимир Трунов

Имея дело с драгоценным металлом, приходится постоянно заботиться о его расходе. Часто хочется заранее знать, сколько примерно будет весить изделие еще до того, как оно будет изготовлено. В большинстве случаев это можно посчитать.

В этой рубрике собраны несколько статей с формулами для расчета массы деталей различной формы. Почему массы, а не веса? Короткий ответ: грамм массы обозначается буквой «г», а грамм веса — буквой «Г», и мне лень нажимать Shift. Длинный ответ: масса — это более фундаментальная характеристика объекта, чем его вес. Например, кольцо массой в 10 г на Земле будет весить 10 Г, а на Луне — только 1,65 Г. Мало того, даже и на Земле вес предмета меняется в зависимости от нашего местоположения: то, что на полюсе весит тонну, на экваторе будет весить всего лишь 995 кГ. Поэтому есть смысл покупать картошку на экваторе и продавать ее на полюсе. И поэтому же есть смысл вычислять именно массу изделия, а не его вес. Да и Shift, опять же, лишний раз нажимать не придется.

Общий подход к вычислению массы детали заключается в вычислении ее объема, который затем умножается на плотность ее материала. Плотность — это масса одного кубического сантиметра этого материала. Ниже приведены таблицы значений плотности некоторых металлов и сплавов.

Несколько слов о единицах измерения. Размеры в ювелирном деле принято измерять в миллиметрах, поэтому объем, полученный из формул, будет измеряться в кубических миллиметрах. А поскольку плотность выражается в граммах на кубический сантиметр, то наш объем надо разделить на 1000, прежде чем умножать его на плотность (в одном кубическом сантиметре — 1000 кубических миллиметров, хоть сразу и не подумаешь!).

И последнее замечание. Полученные по формулам значения массы могут отличаться от реальных на несколько процентов. Это не потому, что формулы не точные, а потому, что в жизни всё чуть сложнее, чем в математике: прямые углы — не совсем прямые, круг и сфера — не идеальные, деформация заготовки при гибке, чеканке и выколотке приводит к неравномерности ее толщины, и можно перечислить еще кучу отклонений от идеала. Последний удар по нашему стремлению к точности наносят шлифовка и полировка, которые приводят к плохо предсказуемым потерям массы изделия. Поэтому к полученным значениям следует относиться как к ориентировочным.

1. Плотность металлов

2. Плотность золотых сплавов

3. Плотность серебряных сплавов

4. Плотность медных сплавов

Цилиндр. Формулы и свойства цилиндра

Цилиндрическая поверхность — это поверхность, полученная путем перемещения прямой (образующей) параллельно самой себе по плоской кривой.

Основания цилиндра представляют собой плоские фигуры, образованные пересечением цилиндрической поверхности с двумя плоскостями.

Определение. Образующая цилиндра г представляет собой комбинацию всех параллельных сегментов (AB), которые соединяют основания цилиндров.

Цилиндр круговой правый

Обычно слово цилиндр понимается как относящееся к конечному сечению правого кругового цилиндра конечной высоты с круговыми концами, перпендикулярными оси.

Правый круговой цилиндр описывается как трехмерная форма, которая образуется путем вращения прямоугольника на своей стороне на 360 °. В этом случае образуется правильный круговой цилиндр с кругом в основании цилиндра.

Определение. Радиус цилиндра r цилиндра — это радиус баз.

Определение. Диаметр цилиндра d — диаметр оснований.

Определение. Высота цилиндра h — расстояние между основаниями цилиндра.

Определение. Ось — это линия, проходящая через центры оснований цилиндров.

Определение. Площадь поверхности , состоящая из боковой части (боковой части), верхней части и нижней части.

Определение. Осевое сечение — это сечение плоскости цилиндра, проходящее через ось цилиндра.

Определение. Касательная плоскость к цилиндру — это плоскость, проходящая через образующую цилиндра и перпендикулярная осевому сечению цилиндра.

Формула. Объем цилиндра :

V = πr ² h = π	d ²	h,
	4

где r — радиус основания, h — высота цилиндра, d — диаметр основания. Формула. Боковое сечение (A _l) по радиусу и высоте:

A _l = 2πrh = πdh

Формула. Площадь поверхности (A _s) по радиусу и высоте:

A _с = 2πr (h + r)

Если основания (верхняя и нижняя поверхности) не параллельны, цилиндр называется наклонным (рис.2).

Если основания не перпендикулярны высоте, цилиндр называется наклонным (рис. 3).

Объем цилиндра с вычислителем

Объем цилиндра с калькулятором — Math Open Reference

Определение: Количество кубических единиц, которое точно заполнит цилиндр.

Попробуй это Перетащите оранжевую точку, чтобы изменить размер цилиндра. Объем рассчитывается при перетаскивании.

Как найти объем цилиндра

Хотя цилиндр технически не является призмой, он обладает многими свойствами призмы.Как призмы, объем находится путем умножения площади одного конца цилиндра (основания) на его высоту.

Поскольку конец (основание) цилиндра представляет собой круг, площадь этого круга определяется формулой:

Умножая на высоту h получаем где:
π — Pi, приблизительно 3,142
r — радиус кругового конца цилиндра
h высота цилиндра

Калькулятор

Используйте калькулятор выше, чтобы рассчитать высоту, радиус или объем цилиндра.

Введите любые два значения, и будет вычислено недостающее. Например: введите радиус и высоту и нажмите «Рассчитать». Объем будет рассчитан.

Аналогичным образом, если вы введете высоту и объем, будет рассчитан радиус, необходимый для получения этого объема.

Объем частично заполненного баллона

Одно из практических применений — это горизонтальный цилиндрический резервуар, частично заполненный жидкостью. Используя приведенную выше формулу, вы можете найти объем цилиндра, обеспечивающий его максимальную вместимость, но вам часто нужно знать объем жидкости в резервуаре с учетом глубины жидкости.

Это можно сделать, используя методы, описанные в Объем горизонтального цилиндрического сегмента.

Наклонные цилиндры

Напомним, что наклонный цилиндр это тот, который «наклоняется», когда верхний центр не находится над базовой центральной точкой. На рисунке выше отметьте «разрешить наклон» и перетащите верхнюю оранжевую точку в сторону, чтобы увидеть наклонный цилиндр.

Оказывается, для них формула объема работает одинаково. Однако вы должны использовать в формуле перпендикулярную высоту.Это вертикальная линия слева на рисунке выше. Чтобы проиллюстрировать это, отметьте «Высота фиксации». Перетаскивая верхнюю часть цилиндра влево и вправо, наблюдайте за вычислением объема и обратите внимание, что объем никогда не меняется.

См. Наклонные цилиндры для более глубокого обсуждения того, почему это так.

Квартир

Помните, что радиус и высота должны быть в одних и тех же единицах — при необходимости преобразуйте их. Результирующий объем будет в этих кубических единицах. Так, например, если высота и радиус указаны в сантиметрах, то объем будет в кубических сантиметрах.

Что попробовать

На рисунке выше нажмите «сбросить» и «скрыть детали».
Перетащите две точки, чтобы изменить размер и форму цилиндра.
Рассчитать объем этого цилиндра
Нажмите «показать подробности», чтобы проверить свой ответ.

Связанные темы

Массовый момент по уравнениям инерции | Инженеры Edge

Связанные ресурсы: механические станки

Уравнение массового момента инерции

Прочность и механика материалов

Момент инерции массы, обычно обозначаемый I, измеряет степень сопротивления объекта ускорению вращения вокруг оси и является вращательным аналогом массы. Моменты инерции масс имеют размерность масса × длина ².Его не следует путать со вторым моментом площади, который используется при расчетах изгиба.

Геометрически простые объекты имеют моменты инерции, которые могут быть выражены математически, но может быть непросто символически выразить момент инерции более сложных тел.

Точечная масса m (масса) на расстоянии r от оси вращения.

I = м R ²

Где:

I = момент инерции (фунт-м · фут ², кг · м ²)
m = масса (фунт-м, кг)
R = расстояние между осью и массой вращения (футы, м)

Моменты всех остальных моментов инерции объекта вычисляются из суммы моментов.

I = ∑ _i m _i R _i ² = m ₁ R ₁ ² + m ₂ R ₂ ² + ….. + m _n R _n ²

Массовый момент инерции

Инерция обычно выражается как

I = к м R ²

Где:

k = инерционная постоянная
m = масса (фунт · м, г)
R = расстояние между осью и массой вращения (дюйм., мм)

Общие уравнения и калькулятор Расчет момента инерции массы ator

Некоторые типичные тела и их моменты инерции

Момент инерции цилиндра

Тонкостенный полый цилиндр :

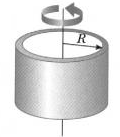
Моменты инерции тонкостенного полого цилиндра сопоставимы с точечной массой и могут быть выражены как:

I = м R ²

Где:

м = масса полости (фунт м, кг)
R = расстояние между осью и тонкостенной полостью (футы, м)

Калькулятор массового момента инерции тонкостенного вала

Массовый момент инерции полого цилиндра (вала):

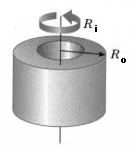
I = 1/2 м (R _i ² + R _o ²)

Где:

м = масса полости (фунт-метр, кг)
R _i = расстояние между осью и внутренней полостью (дюймы, мм)
R _o = расстояние между осью и внешней полостью (дюймы, мм)

Калькулятор массового момента инерции вала полого цилиндра

Цельный цилиндр :

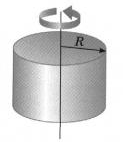
I = 1/2 м R ²

Где:

м = масса цилиндра (фунт-м, кг)
R = расстояние между осью и внешним цилиндром (дюймы, мм)

Калькулятор массового момента инерции цилиндра со сплошным валом

Массовая инерция сферы

Тонкостенная полая сфера :

I = 2/3 м R ²

Где:

м = масса полой сферы (фунт · м, кг)
R = расстояние между осью и полостью (дюймы, мм)

Калькулятор массового момента инерции тонкостенной сферы

Твердая сфера :

I = 2/5 м R ²

Где:

м = масса сферы (фунт · м, кг)
R = радиус в сфере (дюймы, мм)

Уравнение и калькулятор цилиндра твердой сферы Момент инерции массы

Плоскость прямоугольная

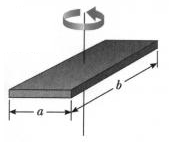
Моменты инерции для прямоугольной плоскости с осью, проходящей через центр :

I = m (a ² + b ²) / 12

Где:

a, b = короткая и длинная стороны (дюймы, мм)
m = масса шара (фунт · м, кг)

Калькулятор массового момента инерции для прямоугольной плоскости

Моменты инерции для прямоугольной плоскости с осью вдоль кромки:

I = (м ²) / 3

Где:

a = длина с обеих сторон (дюймы, мм)
m = масса шара (фунт · м, кг)

Калькулятор массового момента инерции прямоугольной пластины на кромке

Стержень тонкий

Моменты инерции тонкого стержня с осью через центр:

I = (м L ²) / 12

Где:

L = длина стержня (дюйм., мм)
m = масса шара (фунт · м, кг)

Калькулятор момента инерции тонкой штанги

Моменты инерции тонкого стержня с осью:

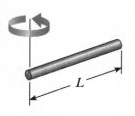
I = 1/3 м L ²

L = длина стержня (дюймы, мм)
m = масса шара (фунт · м, кг)

Калькулятор момента инерции тонкой штанги о кромке

Массовый момент инерции

Массовый момент инерции (момент инерции) — I — это мера сопротивления объекта изменению направления вращения. Момент инерции имеет такое же отношение к угловому ускорению, как масса к линейному ускорению.

Момент инерции тела зависит от распределения массы в теле относительно оси вращения

Для точечной массы Момент инерции равен массе, умноженной на квадрат перпендикулярного расстояния к вращению. оси отсчета и может быть выражено как

I = mr ² (1)
, где
I = момент инерции ( кг · м ² , оторочка футов ², фунт _f фут ²)

м = масса (кг, снаряды)
r = расстояние между осью и массой вращения (м, футы)

Пример — Момент инерции отдельной массы

Создание 3D-моделей с помощью бесплатного расширения Engineering ToolBox Sketchup Extension

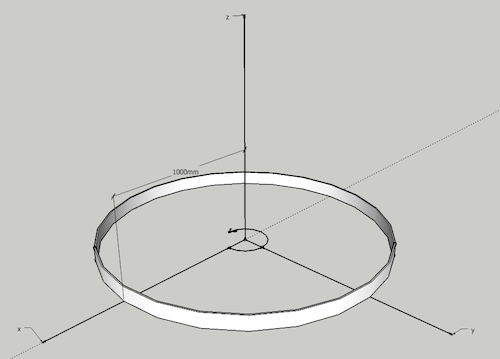
Момент инерции с h относительно вращения вокруг оси z единичной массы 1 кг , распределенной в виде тонкого кольца, как показано на рисунке выше, можно рассчитать как

I _z = (1 кг) ((1000 мм ) (0.001 м / мм)) ²

= 1 кг м ²

Момент инерции — распределенные массы

Точечная масса является основой для всех других моментов инерции, поскольку любой объект может быть «построен». «из набора точечных масс.

I = ∑ _i m _i r _i ² = m ₁ r ₁ ² + m ₂ r ₂ ² + ….. + m _n r _n ² (2)

Для твердых тел с непрерывным распределением соседних частиц формулу лучше выразить в виде интеграла

I = ∫ r ² дм (2b)
где
дм = масса бесконечно малой части тела

Преобразование между единицами измерения момента инерции

^{— 4,21 10 2}6 10 ⁷

149 Умножить на
149 от							до
кг · м ²	г · см ²	фунтов _м футов ²		фунтов ^{4 пуля футов ²}	пуля в ²
кг м ²	1	1 10 ⁷	2.37 10 ¹	3,42 10 ³	7,38 10 ^-1	1,06 10 ²
г см ²	1 10 ^-7	1		2,37 10 ^-6	3,42 10 ^-4	7,38 10 ^-8	1,06 10 ⁵
фунтов _м футов ²	4.21 10 ⁵	1	1,44 10 ²	3,11 10 ^-2	4,48
фунтов _м дюйм ²	2,93 10 6	2,93 10 ³	6,94 10 ^-3	1	2,16 10 ^-4	3,11 10 ^-2
оторочка фут ²	1,36
3,22 10 ¹	4,63 10 ³	1	1,44 10 ²
вставка в ²	9,42 10 6- 9,42 10 ⁴	2,23 10 ^-1	3,22 10 ¹	6,94 10 ^-3	1

Момент инерции — общая формула

Общее выражение инерции уравнение:

I = kmr ² (2c)
где
k = инерционная постоянная — в зависимости от формы тела

Радиус вращения (в )

Радиус вращения — это расстояние от оси вращения, где сосредоточенная точечная масса равна Моменту инерции t. он собственное тело.Радиус вращения тела может быть выражен как

r _g = (л / м) ^1/2 (2d)

где

r _g = радиус вращения ( м, футы)

I = момент инерции корпуса ( кг · м ² , снаряд ft ²)

м = масса тела (кг, пробки)

Некоторые типичные тела и их моменты инерции

Цилиндр

Тонкостенный полый цилиндр

Моменты инерции для полого тонкостенного цилиндра сравнимы с точечной массой (1) и могут быть выражены как :

I = mr ² (3a)
, где
m = масса полости (кг, снаряды)
r = расстояние между ось n и тонкостенная полость (м, футы)
r _o = расстояние между осью и внешней полостью (м, футы)

Полый цилиндр

I = 1/2 м (r _i ² + r _o ²) (3b)
где
м = масса полости (кг, снаряды)
r _i = расстояние между осью и внутренняя полость (м, футы)
r _o = расстояние между осью и внешней полостью (м, футы)

Цельный цилиндр

I = 1/2 mr ² (3c)
где
m = масса цилиндра (кг, заготовки)
r = расстояние между осью и внешним цилиндром (м, футы)

Круглый диск

90 002 I = 1/2 mr ² (3d)
, где
m = масса диска (кг, снаряды)
r = расстояние между осью и внешним диском (м, футы)

Сфера

Тонкостенная полая сфера

I = 2/3 mr ² (4a)
где
m = масса полой сферы (кг,
)
r = расстояние между осью и полостью (м, фут)

Сплошная сфера

I = 2/5 mr ² (4b)
, где
м = масса сферы (кг, снаряды)
r = радиус в сфере (м, фут)

Прямоугольная плоскость

Моменты инерции для прямоугольной плоскости с ось через центр может быть выражена как

I = 1/12 м (a ² + b ²) (5)
, где
a, b = короткая и длинная стороны

Моменты инерции для прямоугольной плоскости с осью вдоль кромки могут быть выражены как

I = 1/3 ма ² (5b)

Slender Rod

Моменты инерции для тонкого стержня с осью через центр можно выразить как

I = 1/12 м L ² (6)
, где
L = длина стержня

Моменты инерции для тонкого стержня с осью сквозной конец может быть выражен как

I = 1/3 м L ² (6b)

Расчет массы цилиндра — однородного и полого

Что такое цилиндр?

Объем и площадь поверхности

Определение массы цилиндра

Расчет массы медного цилиндра

Однородный и полый цилиндры

Масса сплошной детали | Математика для ювелиров

1. Масса параллелепипеда (бруска)

2. Масса цилиндра

3. Масса шара

4. Масса сегмента шара

5. Масса конуса

6. Масса усеченного конуса

7. Масса пирамиды

8. Масса усеченной пирамиды

Калькулятор массы

Расчет массы цилиндра — однородного и полого — OneKu

Что такое цилиндр?

Объем и площадь поверхности

Определение массы цилиндра

Расчет массы медного цилиндра

Однородный и полый цилиндры

Расчет массы полого цилиндра

Масса полой детали | Математика для ювелиров

1. Масса трубки (полого цилиндра)

2. Масса полого (пустотелого) шара

3. Масса полого сегмента шара

4. Масса полого усеченного конуса

5. Масса полой усеченной пирамиды

Расчет массы однородного и полого цилиндров

Определение массы цилиндра

Расчет массы медного цилиндра

Однородный и полый цилиндры

Расчет массы полого цилиндра

Введение к вычислению масс | Математика для ювелиров

1. Плотность металлов

2. Плотность золотых сплавов

3. Плотность серебряных сплавов

4. Плотность медных сплавов

Цилиндр. Формулы и свойства цилиндра

Цилиндр круговой правый

Объем цилиндра с вычислителем

Как найти объем цилиндра

Калькулятор

Объем частично заполненного баллона

Наклонные цилиндры

Квартир

Что попробовать

Связанные темы

Массовый момент по уравнениям инерции | Инженеры Edge

Уравнение массового момента инерции

Массовый момент инерции

Некоторые типичные тела и их моменты инерции

Момент инерции цилиндра

Массовая инерция сферы

Стержень тонкий

Массовый момент инерции

Пример — Момент инерции отдельной массы

Момент инерции — распределенные массы

Преобразование между единицами измерения момента инерции

Момент инерции — общая формула

Радиус вращения (в )

Некоторые типичные тела и их моменты инерции

Цилиндр

Тонкостенный полый цилиндр

Полый цилиндр

Цельный цилиндр

Круглый диск

Сфера

Тонкостенная полая сфера

Сплошная сфера

Прямоугольная плоскость

Slender Rod

Добавить комментарий Отменить ответ