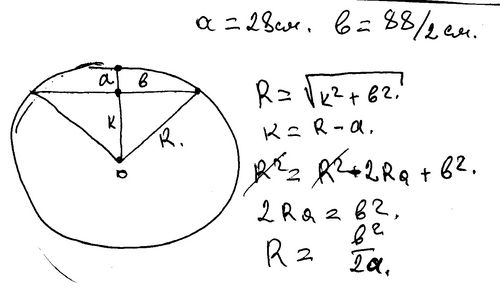Онлайн калькулятор: Сегмент круга
Сегмент кругаКруговой сегмент — часть круга ограниченная дугой и секущей (хордой).
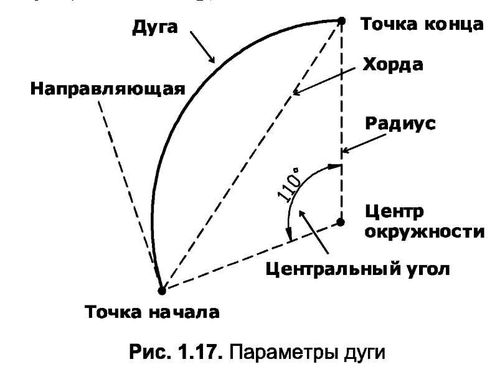
На рисунке:
L — длина дуги сегмента
c — хорда
R — радиус
a — угол сегмента
h — высота
Первый калькулятор рассчитывает параметры сегмента, если известен радиус и угол по следующим формулам:
Формулы вычисления параметров сегмента
Площадь сегмента:
[1]
Длина дуги:
Длина хорды:
Высота сегмента:
Сегмент
Угол в градусах, образуемый радиусами сектора
Точность вычисленияЗнаков после запятой: 2
content_copy Ссылка save Сохранить extension Виджет
Однако, как справедливо заметил наш пользователь:«на практике часто случается, что как радиус дуги, так и угол неизвестны» (см. длина дуги ). Для этого случая для расчета площади сегмента и длины дуги можно использовать следующий калькулятор:
Параметры сегмента по хорде и высоте
Точность вычисленияЗнаков после запятой: 2
Угол (градусы)
content_copy Ссылка save Сохранить extension Виджет
Калькулятор вычисляет радиус круга по длине хорды и высоте сегмента по следующей формуле:
Далее, зная радиус и длину хорды, легко найти угол сегмента по формуле:
Остальные параметры сегмента вычисляются аналогично первому калькулятору, по формулам, приведенным в начале статьи.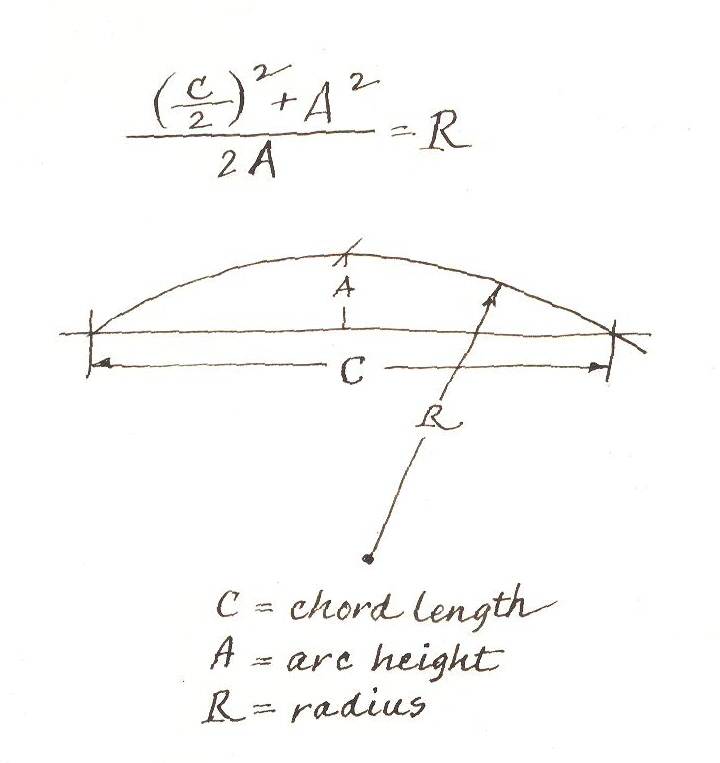
Следующий калькулятор вычисляет площадь сегмента по высоте и радиусу:
Площадь сегмента круга по радиусу и высоте
Точность вычисленияЗнаков после запятой: 2
Угол (градусы)
content_copy Ссылка save Сохранить
Этот калькулятор вычисляет угол из высоты и радиуса по следующей формуле:
далее используется формула [1] для получения площади.
15 вычислений по сегменту круга в одной программе
Последний калькулятор включает в себя все оставшиеся вычисления параметров кругового сегмента:
- длина дуги
- угол
- хорда
- высота
- радиус
- площадь
Выберите два известных аргумента и калькулятор выдаст вам все оставшиеся.
Круговой сегмент — все варианты расчета
ВысотаДлина дугиПлощадьРадиусУгол в градусахХордаВысотаДлина дугиПлощадьРадиусУгол в градусахХорда Показать формулыТочность вычисленияЗнаков после запятой: 2
Угол (градусы)
Файл очень большой, при загрузке и создании может наблюдаться торможение браузера.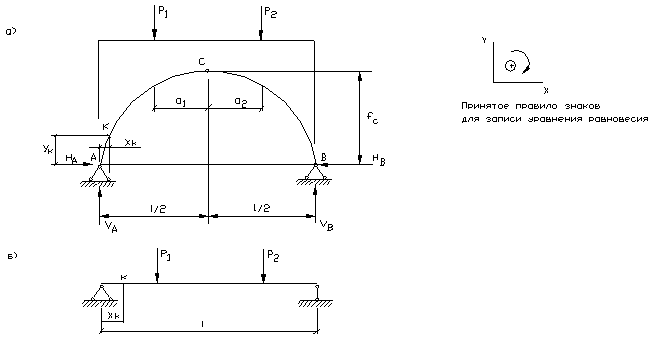
Загрузить close
content_copy Ссылка save Сохранить extension Виджет
Сегмент круга — расчет параметров онлайн
Данный калькулятор считает параметры сегмента круга, а именно:
Перед вами 2 калькулятора, чтобы рассчитать параметры сегмента:
1) сегмент круга решается с помощью радиуса (R) и угла (A).
2) сегмент круга находим с помощью высоты и длины хорды.
The field is not filled.
‘%1’ is not a valid e-mail address.
Please fill in this field.
The field must contain at least% 1 characters.
The value must not be longer than% 1 characters.
Field value does not coincide with the field ‘%1’
An invalid character. Valid characters:’%1′.
Expected number.
It is expected a positive number.
Expected integer.
It is expected a positive integer.
The value should be in the range of [%1 . . %2]
. %2]
The ‘% 1’ is already present in the set of valid characters.
The field must be less than 1%.
The first character must be a letter of the Latin alphabet.
Su
Mo
Tu
We
Th
Fr
Sa
January
February
March
April
May
June
July
August
September
October
November
December
century
B.C.
%1 century
An error occurred while importing data on line% 1. Value: ‘%2’. Error: %3
Unable to determine the field separator. To separate fields, you can use the following characters: Tab, semicolon (;) or comma (,).
%3.%2.%1%4 %6:%7
s.sh.
u.sh.
v.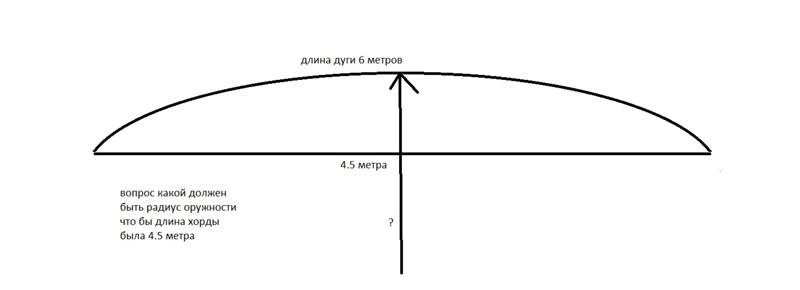 d.
d.
z.d.
yes
no
Wrong file format. Only the following formats: %1
Please leave your phone number and / or email.
Найти длину дуги линии онлайн калькулятор. Определение длины дуги
Сначала разберемся в отличии между кругом и окружностью. Чтобы увидеть эту разницу, достаточно рассмотреть, чем являются обе фигуры. Это бесчисленное количество точек плоскости, располагающиеся на равном расстоянии от единственной центральной точки. Но, если круг состоит и из внутреннего пространства, то окружности оно не принадлежит. Получается, что круг это и окружность, ограничивающая его (о-кру(г)жность), и бесчисленное число точек, что внутри окружности.
Для любой точки L , лежащей на окружности, действует равенство OL=R . (Длина отрезка OL равняется радиусу окружности).
Отрезок, который соединяет две точки окружности, является ее хордой .
Хорда, проходящая прямо через центр окружности, является диаметром этой окружности (D)
. {\circ}}
{\circ}}
Диаметр, что перпендикулярен хорде, делит хорду и стянутые ею дуги пополам.
В случае, если хорды AB и CD окружности имеют пересечение в точке N , то произведения отрезков хорд, разделенные точкой N , равны между собой.
AN\cdot NB = CN \cdot ND
Касательная к окружности
Касательной к окружности принято называть прямую, у которой имеется одна общая точка с окружностью.
Если же у прямой есть две общие точки, ее называют секущей .
Если провести радиус в точку касания, он будет перпендикулярен касательной к окружности.
Проведем две касательные из этой точки к нашей окружности. Получится, что отрезки касательных сравняются один с другим, а центр окружности расположится на биссектрисе угла с вершиной в этой точке.
AC = CB
 {\circ}
{\circ}\angle ADB = \angle AEB = \angle AFB
На одной окружности находятся вершины треугольников с тождественными углами и заданным основанием.
Угол с вершиной внутри окружности и расположенный между двумя хордами тождественен половине суммы угловых величин дуг окружности, которые заключаются внутри данного и вертикального углов.
\angle DMC = \angle ADM + \angle DAM = \frac{1}{2} \left (\cup DmC + \cup AlB \right)
Угол с вершиной вне окружности и расположенный между двумя секущими тождественен половине разности угловых величин дуг окружности, которые заключаются внутри угла.
\angle M = \angle CBD — \angle ACB = \frac{1}{2} \left (\cup DmC — \cup AlB \right)
Вписанная окружность
Вписанная окружность — это окружность, касающаяся сторон многоугольника.
В точке, где пересекаются биссектрисы углов многоугольника, располагается ее центр.
Окружность может быть вписанной не в каждый многоугольник.
Площадь многоугольника с вписанной окружностью находится по формуле:
S = pr ,
r — радиус вписанной окружности.
Отсюда следует, что радиус вписанной окружности равен:
r = \frac{S}{p}
Суммы длин противоположных сторон будут тождественны, если окружность вписана в выпуклый четырехугольник. И наоборот: в выпуклый четырехугольник вписывается окружность, если в нем суммы длин противоположных сторон тождественны.
AB + DC = AD + BC
В любой из треугольников возможно вписать окружность. Только одну единственную. В точке, где пересекаются биссектрисы внутренних углов фигуры, будет лежать центр этой вписанной окружности.
Радиус вписанной окружности вычисляется по формуле:
r = \frac{S}{p} ,
где p = \frac{a + b + c}{2}
Описанная окружность
Если окружность проходит через каждую вершину многоугольника, то такую окружность принято называть описанной около многоугольника . {\circ}
{\circ}
Около любого треугольника можно описать окружность, причем одну-единственную. Центр такой окружности будет расположен в точке, где пересекаются серединные перпендикуляры сторон треугольника.
Радиус описанной окружности можно вычислить по формулам:
R = \frac{a}{2 \sin A} = \frac{b}{2 \sin B} = \frac{c}{2 \sin C}
R = \frac{abc}{4 S}
a , b , c — длины сторон треугольника,
S — площадь треугольника.
Теорема Птолемея
Теорема Птолемея гласит, что произведение диагоналей тождественно сумме произведений противоположных сторон вписанного четырехугольника.
AC \cdot BD = AB \cdot CD + BC \cdot AD
Углом называется геометрическая фигура, которая образована двумя лучами – сторонами угла, исходящими из одной точки – вершины угла. Обычно для построения плоского угла в планиметрии используется транспортир, с помощью которого можно легко отложить угол с заданной градусной мерой, но как быть, если под рукой этого инструмента нет?Для построения угла можно воспользоваться тригонометрическими функциями и построением прямоугол ьного треугол ьника.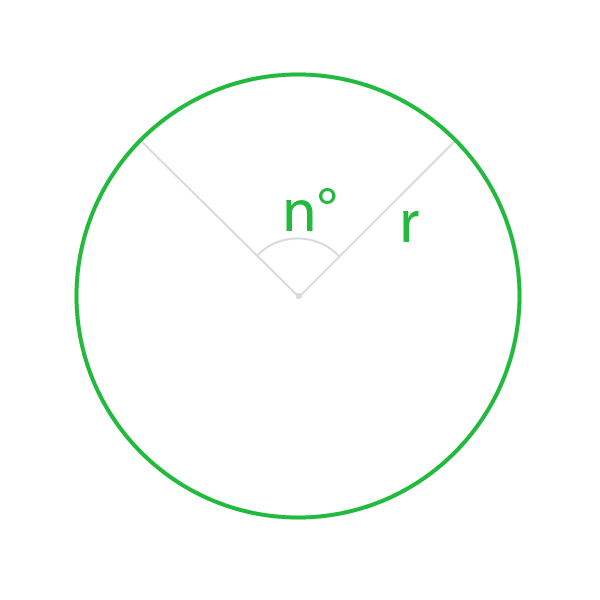
Вам понадобится
- Полная таблица тангенсов, линейка
Инструкция
Пусть стоит задача построить угол некоторой размерности?.
Построим отрезок AB произвольной . Использую соотношение катетов в угол ьном треугол ьнике можно BC этого треугол ьника BC = AB tg?, тангенса угла? можно узнать по .
Далее от точки A необходимо отложить отрезок длины BC перпендикулярно отрезку AB.
Видео по теме
Обратите внимание
Для построения углов ∠α ≥ 90º, необходимо построить угол ∠β
Все чаще в повседневной практике приходится решать задачи, которые когда-то как семечки щелкали на уроках математики, но по прошествии лет, что-то подзабылось. Нахождение длины дуги окружности — одна из задач, с которой человек может столкнуться в жизни.
Вам понадобится
- калькулятор, значение числа π = 3,14 , значение радиуса r и центрального угла α, взятых из условия задачи.
Инструкция
Для начала нужно определиться с понятиями. Окружность — это множество всех точек плоскости, находящихся на данном положительном расстоянии от некоторой данной точки плоскости, называемой центром (точка О). Дуга — часть окружности , расположенная между А и В этой окружности , где ОА и ОВ радиусы этой окружности . Чтобы различать эти дуги , на каждой из них отмечают промежуточную L и М. Таким образом, получаем две дуги ALB и AMB.
Окружность — это множество всех точек плоскости, находящихся на данном положительном расстоянии от некоторой данной точки плоскости, называемой центром (точка О). Дуга — часть окружности , расположенная между А и В этой окружности , где ОА и ОВ радиусы этой окружности . Чтобы различать эти дуги , на каждой из них отмечают промежуточную L и М. Таким образом, получаем две дуги ALB и AMB.
Итак, дуга окружности определяется радиусом окружности r и центральным углом?. Зная эти два , несложно длину дуги L по формуле:
L = ?r?/180
где? — числовая константа равная 3,14.
Подставив в формулу значения?, r, ? и вооружившись калькулятором, вы легко вычислите длину дуги L.
Длиной принято обозначать расстояние между двумя точками какого-либо отрезка. Это может быть прямая, ломаная или замкнутая линия. Вычислить длину можно довольно простым путем, если знать некоторые другие показатели отрезка.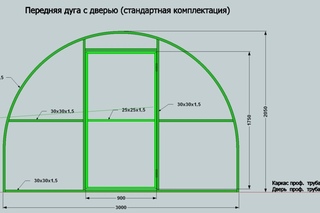
Инструкция
Если вам нужно найти длину стороны квадрата, то это не составит , если вам известна его площадь S. В связи с тем, что все стороны квадрата имеют , вычислить величину одной из них можно по формуле: a = √S.
Проектировщикам приходится рассчитывать длину дуги, знач только предположительную высоту моста или перекрытия и длину пролета. В этом случае сделайте чертеж. Пролет будет являться хордой, а высота — частью радиуса. Проведите ее из самой верхней точки будущей арки перпендикулярно к и продолжите дальше, до предполагаемого центра окружности. Высота делит пополам. Центр соедините с концами , получив таким образом еще 2 радиуса. Вычислите радиус по теореме Пифагора, то есть R=√a2+(R-h)2.
Обратите внимание
Две точки делят окружность на две дуги. В задании может быть указано, длину какой из них нужно найти. В этом случае необходимо вычислить больший угол, отняв от полного угла заданный острый.
При вычислении любой длины следует помнить, что это величина конечная, то есть просто число. Если имеется в виду длина дуги кривой , то такая задача решается с помощью определенного интеграла (в плоском случае) или криволинейного интеграла первого рода (по длине дуги). Дуга АВ будет обозначаться UАВ.
Если имеется в виду длина дуги кривой , то такая задача решается с помощью определенного интеграла (в плоском случае) или криволинейного интеграла первого рода (по длине дуги). Дуга АВ будет обозначаться UАВ.
Инструкция
Первый случай (). Пусть UАВ задана плоской кривой y = f(x). Аргумент функции изменятся в пределах от а до b и она непрерывно дифференцируема этом отрезке. Найдем длину L дуги UАВ (см. рис. 1а). Для решения этой задачи разбейте рассматриваемый отрезок на элементарные отрезки ∆xi, i=1,2,…,n. В UАВ разобьется на элементарные дуги ∆Ui, участков графика функции y=f(x) на каждом из элементарных отрезков. Найдете длину ∆Li элементарной дуги приближенно, заменив ее соответствующей хордой. При этом можно приращения заменить дифференциалами и использовать теорему Пифагора. После вынесения из квадратного корня дифференциала dx получите результат, приведенный на рисунке 1b.
Второй случай (дуга UАВ задана параметрически). 2=1, получите формулу для вычисления длины дуги в полярных координатах (см. рис.2b).
2=1, получите формулу для вычисления длины дуги в полярных координатах (см. рис.2b).
Четвертый случай (пространственная кривая, заданная параметрически). x=x(t), y=y(t), z=z(t) tє[α,β]. Строго говоря, здесь следует применить криволинейный первого рода (по длине дуги). Криволинейные вычисляют их определенные. В результате ответ останется практическим таким же как и случае два, с тем лишь отличием, что появится слагаемое – квадрат производной z’(t) (см рис. 2с).
Источники:
- Пискунов Н.С. Дифференциальное и интегральное исчисления. Учебник для ВТУЗов. Т.1.-М.: Наука, 1972.-576 с.
- вычисление длины дуги с помощью определенного интеграла
Дугой называется часть окружности. Окружность — геометрическое место точек, равноудалённых от одной точки, называемой центром. В бытовых ситуациях, когда погрешность не важна и измерения затруднены, длину дуги иногда измеряют с помощью мягкого материала, например нити, который повторяет форму дуги , а затем выпрямляется и измеряется.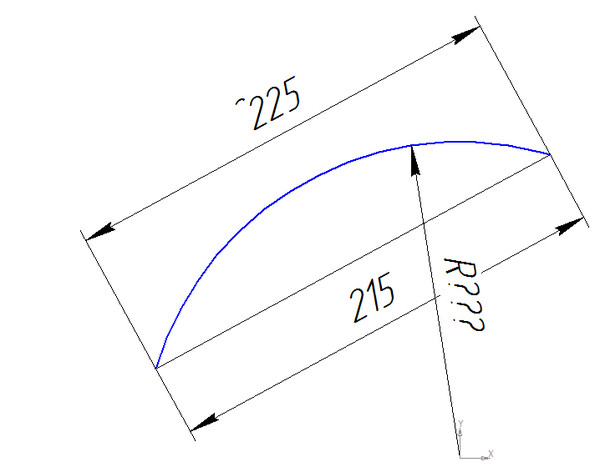 Для серьёзных измерений такой метод неприемлем.
Для серьёзных измерений такой метод неприемлем.
Инструкция
Если длина дуги (l) между крайними точками, задающими хорду, известна, а кроме нее в условиях дан и радиус окружности (R), задачу вычисления длины хорды (m) можно свести к расчету длины основания равнобедренного треугольника. Боковые стороны этого треугольника будут двумя радиусами окружности, а угол между ними будет центральным углом, который вам и нужно рассчитать в первую очередь. Для этого разделите длину дуги на радиус: l/R. Полученный результат выражен в радианах. Если вам удобнее производить вычисления , будет значительно сложнее — сначала умножьте длину дуги на 360, а затем поделите результат на удвоенное произведение Пи на радиус: l*360/(2*π*R) = l*180/(π*R).
Выяснив величину центрального угла, рассчитайте длину хорды . Для этого удвоенный радиус умножьте на синус половины центрального угла. Если вы выбрали расчеты в градусах, в общем виде полученную формулу запишите так: m = 2*R*sin(l*90/(π*R)).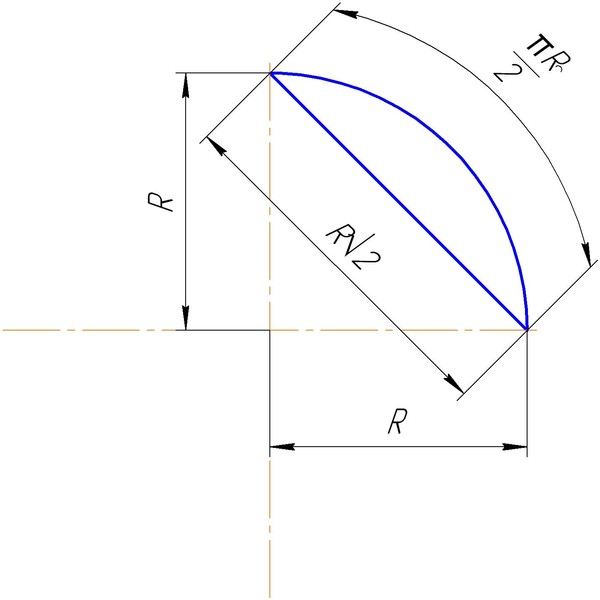 Для расчетов в радианах она будет содержать на одно математическое действие меньше m = 2*R*sin(l/(2*R)). Например, при длине дуги в 90 см и радиусе 60 см должна иметь длину 2*60*sin(90*90/(3,14*60)) = 120*sin(8100/188,4) = 120*sin(42,99°) ≈ 120*0,68 = 81,6 см при точности расчетов до двух после запятой.
Для расчетов в радианах она будет содержать на одно математическое действие меньше m = 2*R*sin(l/(2*R)). Например, при длине дуги в 90 см и радиусе 60 см должна иметь длину 2*60*sin(90*90/(3,14*60)) = 120*sin(8100/188,4) = 120*sin(42,99°) ≈ 120*0,68 = 81,6 см при точности расчетов до двух после запятой.
Если в дополнение к длине дуги (l) в условиях задачи дана полная (L), выразите через нее радиус, разделив на удвоенное Пи. Затем подставьте это выражение в общую формулу из предыдущего шага: m = 2*(L/(2*π))*sin(l*90/(π*L/(2*π))). После упрощения выражения у вас должно получиться равенство для расчетов в градусах: m = L/π*sin(l*180/L). Для вычислений в радианах оно будет выглядеть так: m = L/π*sin(l*π/L). Например, если длина дуги составляет 90 см, а длина окружности — 376,8 см, длина хорды составит 376,8/3,14*sin(90*180/376,8) = 120*sin(42,99°) ≈ 120*0,68 = 81,6 см.
Понятие хорда в школьном курсе геометрии связано с понятием окружность.Окружностью называется плоская фигура, составленная из всех точек этой плоскости равностоящих от заданной плоскости.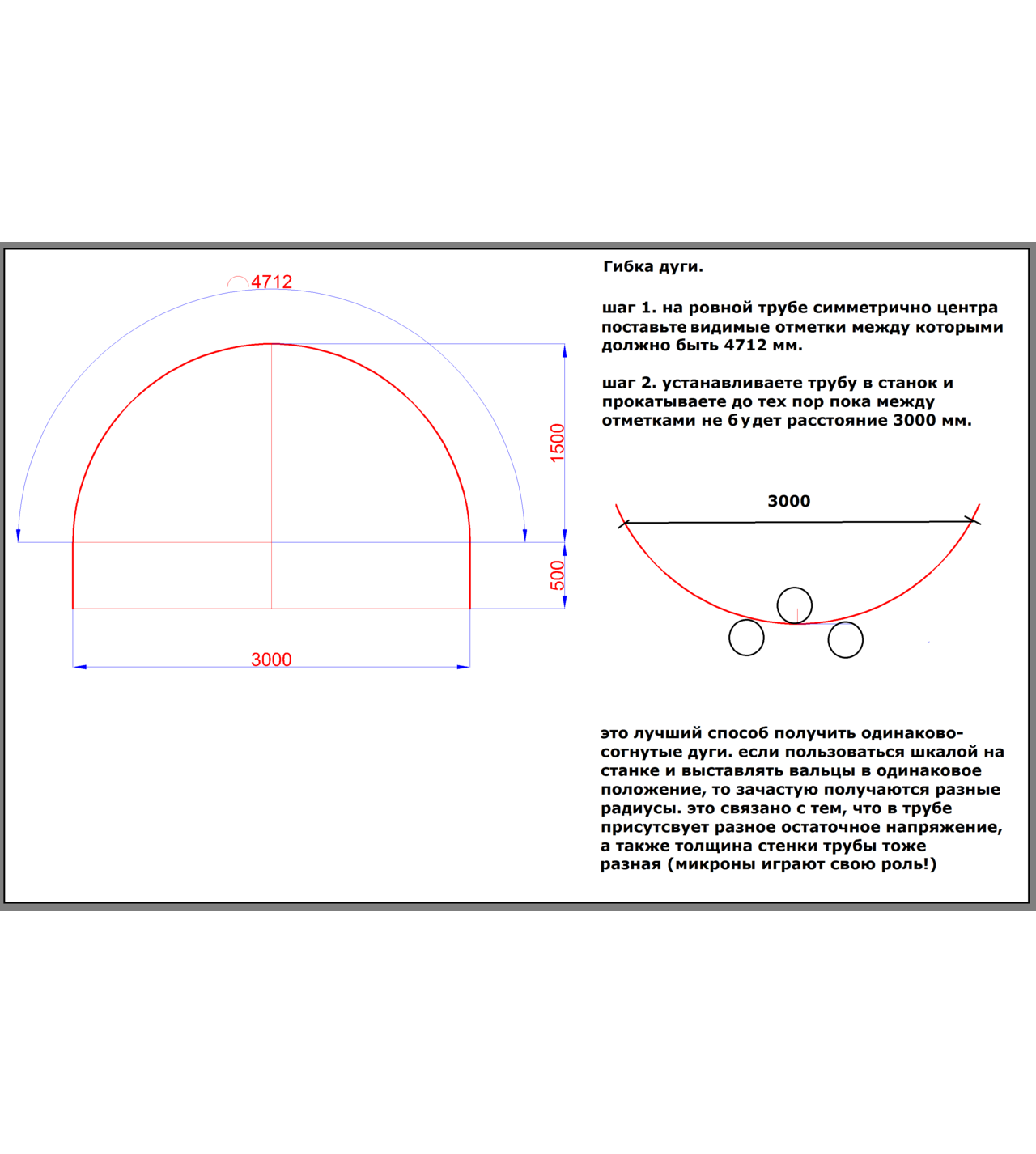 Радиусом окружности называется расстояние от центра до любой точки лежащей на ней.Ходой называется отрезок, соединяющий любые две точки, лежащие на окружности.
Радиусом окружности называется расстояние от центра до любой точки лежащей на ней.Ходой называется отрезок, соединяющий любые две точки, лежащие на окружности.
Инструкция
Для получения длины произвольной хорды необходимо ввести дополнительное .
Угол с вершиной в центре окружности центральным углом этой окружности.
Если известна градусная мера центрального угла??, то длина хорды, на которую она опирается, рассчитывается по формулам
h = 2 * R * sin(??/2)
h = R * v(2 * (1 — cos??))
h = 2 * R * cos??, где?? = (П — ??)/2, П – П
Видео по теме
Все чаще в повседневной практике приходится решать задачи, которые когда-то как семечки щелкали на уроках математики, но по прошествии лет, что-то подзабылось. Нахождение длины дуги окружности — одна из задач, с которой человек может столкнуться в жизни.
Вам понадобится
- калькулятор, значение числа π = 3,14 , значение радиуса r и центрального угла α, взятых из условия задачи.

Инструкция
Для начала нужно определиться с понятиями. Окружность — это множество всех точек плоскости, находящихся на данном положительном расстоянии от некоторой данной точки плоскости, называемой центром (точка О). Дуга — часть окружности , расположенная между А и В этой окружности , где ОА и ОВ радиусы этой окружности . Чтобы различать эти дуги , на каждой из них отмечают промежуточную L и М. Таким образом, получаем две дуги ALB и AMB.
Итак, дуга окружности определяется радиусом окружности r и центральным углом?. Зная эти два , несложно длину дуги L по формуле:
L = ?r?/180
где? — числовая константа равная 3,14.
Подставив в формулу значения?, r, ? и вооружившись калькулятором, вы легко вычислите длину дуги L.
Необходимость вычислить длину дуги может возникнуть при выполнении самых разнообразных проектных работ. Это разработка арочных перекрытий, строительство мостов и тоннелей, прокладка автомобильных и железнодорожных путей и многое другое. Исходные условия для решения этой задачи могут быть очень разными. Для того, чтобы наиболее оптимальным способом вычислить длину дуги, необходимо знать радиус окружности и центральный угол.
Исходные условия для решения этой задачи могут быть очень разными. Для того, чтобы наиболее оптимальным способом вычислить длину дуги, необходимо знать радиус окружности и центральный угол.
Вам понадобится
- — лист бумаги;
- — циркуль;
- — линейка;
- — транспортир;
- — компьютер с программой AutoCAD;
- — калькулятор.
Инструкция
Постройте окружность с заданным радиусом. Принципы ее построение в AutoCAD те же самые, что и на листе бумаги. Освоив способы построения разных геометрических фигур классическим способом, вы очень быстро поймете, как это делается на компьютере. Разница заключается в том, что при обычном построении с помощью циркуля вы находите центр окружности по точке, куда ставится иголка. В AutoCAD найдите в верхнем меню кнопку «arc” или «Дуга». Выберите построение по центру, начальной точке и углу и введите нужные параметры. Обозначьте центр окружности как О.
С помощью карандаша и линейки или компьютерной мыши проведите радиус. Если вы чертите на листе, то с помощью транспортира отложите заданный размер угла. Для этого нулевую отметку транспортира совместите с точкой О, отметьте нужный угол и проведите через полученную точку второй радиус. Угол обозначьте как α. Можно назвать его и АОВ, если соответствующими буквами отметить точки пересечения с окружностью. Вам нужно найти длину дуги АВ.
Если вы чертите на листе, то с помощью транспортира отложите заданный размер угла. Для этого нулевую отметку транспортира совместите с точкой О, отметьте нужный угол и проведите через полученную точку второй радиус. Угол обозначьте как α. Можно назвать его и АОВ, если соответствующими буквами отметить точки пересечения с окружностью. Вам нужно найти длину дуги АВ.
Если размер угла задан в градусах, то длина дуги равна удвоенному произведению радиуса окружности на коэффициент π и на соотношение угла α к полному центрального угла окружность. Он составляет 360°. То есть ее можно найти по формуле L=2πRα/360°, где L – искомая длина дуги, R- радиус окружности, а α – размер угла в градусах. Угол может быть задан и в . Тогда длина дуги равна произведению радиуса на угол, то есть L=Rα. В этом случае остальная часть формулы уже сократилась при переводе градусов в .
Проектировщикам приходится рассчитывать длину дуги, знач только предположительную высоту моста или перекрытия и длину пролета. В этом случае сделайте чертеж. Пролет будет являться хордой, а высота — частью радиуса. Проведите ее из самой верхней точки будущей арки перпендикулярно к и продолжите дальше, до предполагаемого центра окружности. Высота делит
В этом случае сделайте чертеж. Пролет будет являться хордой, а высота — частью радиуса. Проведите ее из самой верхней точки будущей арки перпендикулярно к и продолжите дальше, до предполагаемого центра окружности. Высота делит
Часть фигуры, которая образует окружность, точки которой равноудалены, называется дугой. Если из точки центра окружности, провести лучи в точки, совпадающие с концами дуги, будет образован её центральный угол.
Определение длины дуги
Производится по следующей формуле:
где L – искомая длина дуги, π = 3,14 , r – радиус окружности, α – центральный угол.
Ответ:Длина дуги окружности равна 14,82 сантиметра.
В элементарной геометрии под дугой понимается подмножество окружности, расположенной между двумя расположенными на ней точками. На практике решать задачи по определению ее длины инженерам и архитекторам приходится достаточно часто, поскольку этот геометрический элемент широко распространен в самых разнообразных конструкциях.
Пожалуй, первым, перед кем встала эта задача, были древние зодчие, которым так или иначе приходилось определять этот параметр для сооружения сводов, широко используемых для перекрытия промежутков между опорами в круглых, многоугольных или эллиптических зданиях. Если внимательно присмотреться к дошедшим до наших дней шедеврам древнегреческого, древнеримского и особенно арабского зодчества, то можно заметить, что в их конструкциях дуги и своды встречаются чрезвычайно часто. Творения современных архитекторов ими не так богаты, но эти геометрические элементы наличествуют, конечно же, и в них.
Длину различных дуг необходимо рассчитывать при сооружении автомобильных и железных дорог, а также автодромов, причем во многих случаях от правильности и точности вычислений во многом зависит безопасность движения. Дело в том, что многие повороты магистралей с точки зрения геометрии представляют собой именно дуги, и по движению по ним на транспорт воздействуют различные физические силы. Параметры их результирующей во многом определяются длиной дуги, а также ее центральным углом и радиусом.
Параметры их результирующей во многом определяются длиной дуги, а также ее центральным углом и радиусом.
Конструкторам машин и механизмов приходится вычислить длины различных дуг для правильной и точной компоновки составных частей различных агрегатов. В данном случае ошибки в расчетах чреваты тем, что важные и ответственные детали будут неправильно взаимодействовать друг с другом и механизм просто не сможет функционировать так, как планируют его создатели. В качестве примеров конструкций, изобилующих такими геометрическими элементами, как дуги, можно привести двигатели внутреннего сгорания, коробки переключения передач, дерево- и металлообрабатывающее оборудование, кузовные элементы легковых и грузовых автомобилей и т.д.
Дуги достаточно широко встречаются в медицине, в частности, в стоматологии. Например, они используются для исправления неправильного прикуса. Корректирующие элементы, называемые брекетами (или брекет-системами) и имеющие соответствующую форму, изготавливаются из специальных сплавов, и устанавливаются таким образом, чтобы изменить положение зубов. Само собой разумеется, что для того, чтобы лечение проходило успешно, эти дуги должны быть очень точно рассчитаны. Кроме того, дуги очень широко используются в травматологии, и, пожалуй, самым ярким примером тому является знаменитый аппарат Илизарова, изобретенный российским врачом в 1951 году и чрезвычайно успешно используемый по сей день. Неотъемлемыми его частями являются металлические дуги, снабженные отверстиями, через которые продеваются специальные спицы, и являющиеся основными опорам всей конструкции.
Само собой разумеется, что для того, чтобы лечение проходило успешно, эти дуги должны быть очень точно рассчитаны. Кроме того, дуги очень широко используются в травматологии, и, пожалуй, самым ярким примером тому является знаменитый аппарат Илизарова, изобретенный российским врачом в 1951 году и чрезвычайно успешно используемый по сей день. Неотъемлемыми его частями являются металлические дуги, снабженные отверстиями, через которые продеваются специальные спицы, и являющиеся основными опорам всей конструкции.
- 16.11.2014
На рисунке показана схема простого усилителя мощности класса А на транзисторах. Усилитель имеет выходную мощность порядка 20Вт на 8 Ом нагрузке. Напряжение питания может быть в пределах от 22В до 28В (4А). Источник — http://www.eleccircuit.com/class-a-amplifier-by-transistor/
- 29.09.2014
Данный усилитель предназначен для усиления мощности передатчика карманной радиостанции в диапазоне 144 МГц. При подачи на его вход сигнала мощностью 0,05Вт и питании 24В усилитель выдает мощность 5-6Вт, а при питании его напряжением 12В он выдает 3-4Вт.
 Входное и выходное сопротивления равны 50 Ом. Описание: первый каскад работает в классе …
Входное и выходное сопротивления равны 50 Ом. Описание: первый каскад работает в классе … - 04.10.2014
В промышленных аппаратах используют разные способы регулировки тока: шунтирование с помощью дросселей всевозможных типов, изменение магнитного потока за счет подвижности обмоток или магнитного шунтирования, применение магазинов активных балластных сопротивлений и реостатов. К недостаткам такой регулировки надо отнести сложность конструкции, громоздкость сопротивлений, их сильный нагрев при работе, неудобство при переключении. Наиболее …
- 03.10.2014
На рисунке показана схема простого преобразователя напряжения на TL496. Преобразователь преобразует постоянное напряжение 3В в постоянное напряжение 9В. Преобразователь напряжения весьма прост, он состоит из микросхемы TL496 и конденсатора и дросселя на 50мкГн. Выходной ток преобразователя может достигать 400мА (не гарантировано выходное напряжение 9В). Ток потребления преобразователя без нагрузки 125мкА.

Как по длине дуги вычислить радиус
Гибочный калькулятор
Чаще всего стоит задача определения параметров дуги по её габаритным размерам. Для этого мы предлагаем гибочный калькулятор.
Введите значения H и h в миллиметрах
Не забывайте, что для гибки профилей необходим технологический припуск от 500 до 1000 мм. на заготовку.
Вы можете скачать ПК версию гибочного калькулятора по этой ссылке.
140030, МО, Люберецкий район, пос. Малаховка, Касимовское шоссе, д. 3Г
Право собственности ООО «ПК РАДИУС» © 2002–2017. Все права защищены.
На данной странице калькулятор поможет рассчитать длину дуги окружности онлайн.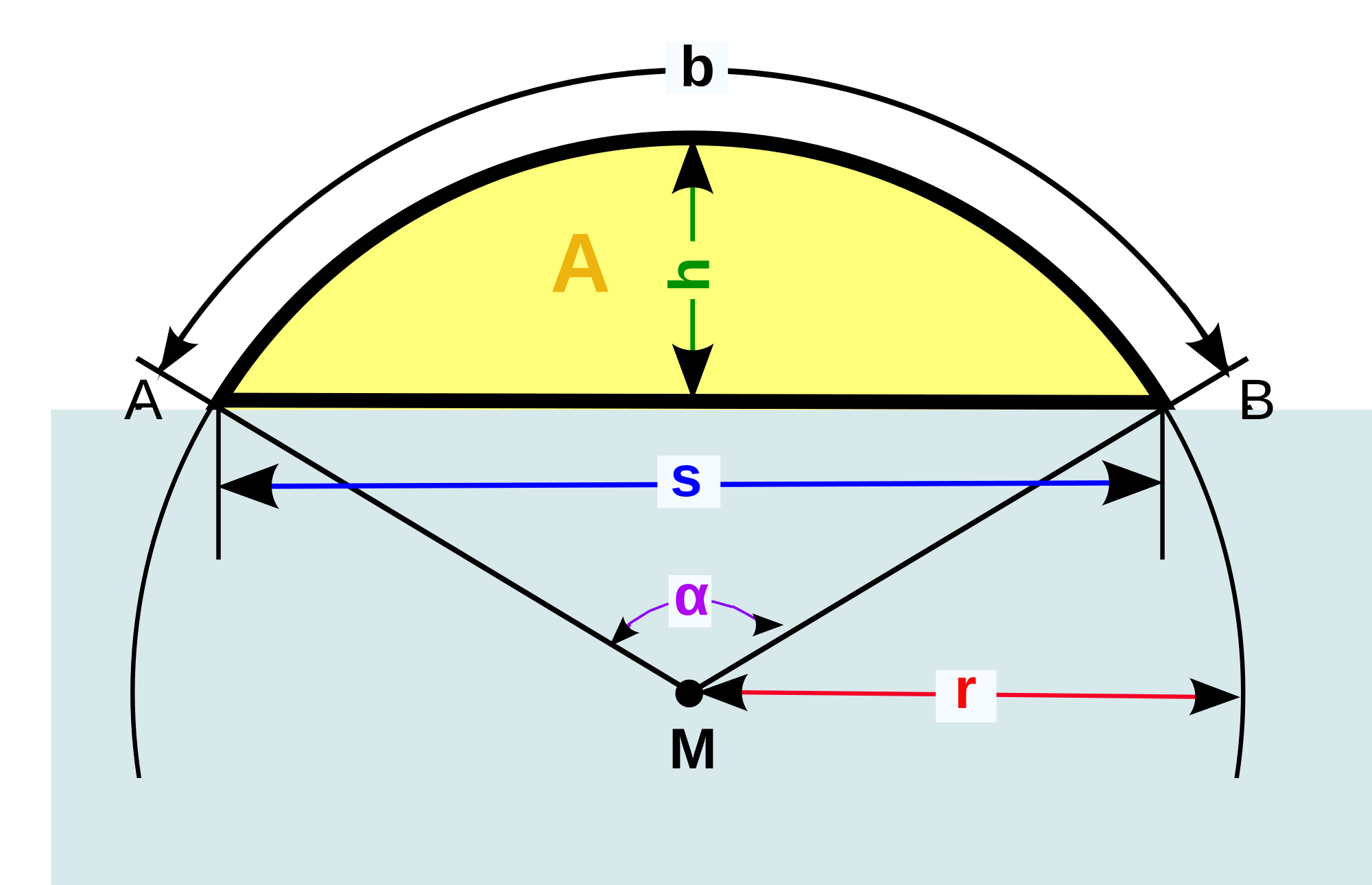 Для расчета задайте радиус, угол между радиусами.
Для расчета задайте радиус, угол между радиусами.
Чтобы найти длину дуги, когда не известен радиус, например, на чертеже или у предмета, то используют формулу Гюйгенса. При расчете по этой формуле есть погрешность, примерно от 0,5% до 0,02%.
Дуга окружности – это часть окружности ограниченная двумя точками.
Онлайн калькулятор для расчёта длины дуги
Выберите в чём измеряется угол:
Решение
Формула расчёта длины дуги
Угол в градусах
- L – длина дуги
- π – число Пи
- r – радиус окружности
- α – угол (в градусах)
Угол в радианах
- L – длина дуги
- r – радиус окружности
- α – угол (в радианах)
Теория
Дуга – это линия, являющаяся частью окружности, у которой все точки равноудалены от центра. Если из точки центра окружности, провести лучи в точки, совпадающие с концами дуги, будет образован её центральный угол.
Похожие калькуляторы:
Калькуляторы ТОП
Сайт большого количества разных онлайн калькуляторов, конвертеров и счётчиков.
Делайте свои расчёты вместе с нами!
вычислить длину дуги
Вы искали вычислить длину дуги? На нашем сайте вы можете получить ответ на любой математический вопрос здесь. Подробное решение с описанием и пояснениями поможет вам разобраться даже с самой сложной задачей и вычислить длину дуги кривой, не исключение. Мы поможем вам подготовиться к домашним работам, контрольным, олимпиадам, а так же к поступлению в вуз. И какой бы пример, какой бы запрос по математике вы не ввели — у нас уже есть решение. Например, «вычислить длину дуги».
Применение различных математических задач, калькуляторов, уравнений и функций широко распространено в нашей
жизни. Они используются во многих расчетах, строительстве сооружений и даже спорте. Математику человек
использовал еще в древности и с тех пор их применение только возрастает. Однако сейчас наука не стоит на
месте и мы можем наслаждаться плодами ее деятельности, такими, например, как онлайн-калькулятор, который
может решить задачи, такие, как вычислить длину дуги,вычислить длину дуги кривой,вычислить длину дуги кривой онлайн калькулятор,длина дуги,длина дуги калькулятор онлайн,длина дуги кривой,длина дуги кривой через интеграл,длина дуги окружности онлайн калькулятор,длина дуги онлайн,длина дуги онлайн калькулятор,длина дуги равна,длина дуги формула,длина дуги через радиус,длина дуги через угол,длина кривой,длина кривой через интеграл,длина полукруга формула,как вычислить длину дуги,как вычислить длину дуги окружности,как найти длину дуги,как найти длину дуги окружности если известен угол,как определить длину дуги,как посчитать длину дуги,как посчитать длину дуги зная радиус,как рассчитать длину дуги,как узнать длину дуги,калькулятор онлайн длина дуги,найти длину дуги,найти длину дуги кривой,найти длину дуги кривой онлайн,найти длину дуги кривой онлайн калькулятор через интеграл,найти длину дуги окружности,найти длину кривой,онлайн калькулятор длина дуги,посчитать длину дуги,рассчитать длину дуги,расчет длины дуги,расчет дуги,расчет дуги онлайн калькулятор,формула длина дуги,формула длина полукруга,формула длины дуги.
Математику человек
использовал еще в древности и с тех пор их применение только возрастает. Однако сейчас наука не стоит на
месте и мы можем наслаждаться плодами ее деятельности, такими, например, как онлайн-калькулятор, который
может решить задачи, такие, как вычислить длину дуги,вычислить длину дуги кривой,вычислить длину дуги кривой онлайн калькулятор,длина дуги,длина дуги калькулятор онлайн,длина дуги кривой,длина дуги кривой через интеграл,длина дуги окружности онлайн калькулятор,длина дуги онлайн,длина дуги онлайн калькулятор,длина дуги равна,длина дуги формула,длина дуги через радиус,длина дуги через угол,длина кривой,длина кривой через интеграл,длина полукруга формула,как вычислить длину дуги,как вычислить длину дуги окружности,как найти длину дуги,как найти длину дуги окружности если известен угол,как определить длину дуги,как посчитать длину дуги,как посчитать длину дуги зная радиус,как рассчитать длину дуги,как узнать длину дуги,калькулятор онлайн длина дуги,найти длину дуги,найти длину дуги кривой,найти длину дуги кривой онлайн,найти длину дуги кривой онлайн калькулятор через интеграл,найти длину дуги окружности,найти длину кривой,онлайн калькулятор длина дуги,посчитать длину дуги,рассчитать длину дуги,расчет длины дуги,расчет дуги,расчет дуги онлайн калькулятор,формула длина дуги,формула длина полукруга,формула длины дуги.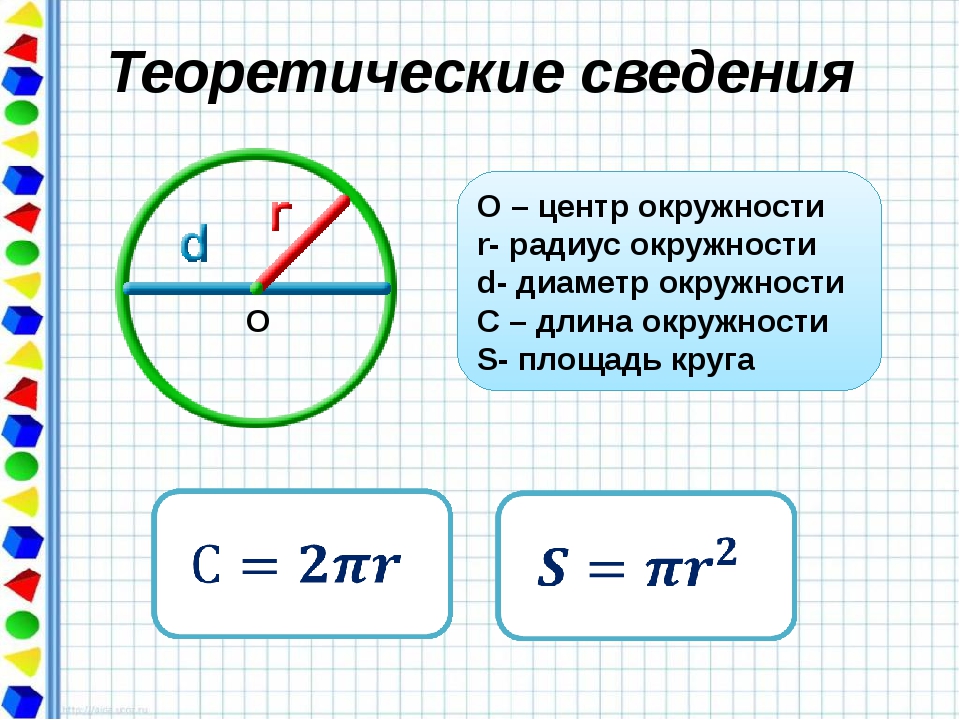 На этой странице вы найдёте калькулятор,
который поможет решить любой вопрос, в том числе и вычислить длину дуги. Просто введите задачу в окошко и нажмите
«решить» здесь (например, вычислить длину дуги кривой онлайн калькулятор).
На этой странице вы найдёте калькулятор,
который поможет решить любой вопрос, в том числе и вычислить длину дуги. Просто введите задачу в окошко и нажмите
«решить» здесь (например, вычислить длину дуги кривой онлайн калькулятор).
Где можно решить любую задачу по математике, а так же вычислить длину дуги Онлайн?
Решить задачу вычислить длину дуги вы можете на нашем сайте https://pocketteacher.ru. Бесплатный онлайн решатель позволит решить онлайн задачу любой сложности за считанные секунды. Все, что вам необходимо сделать — это просто ввести свои данные в решателе. Так же вы можете посмотреть видео инструкцию и узнать, как правильно ввести вашу задачу на нашем сайте. А если у вас остались вопросы, то вы можете задать их в чате снизу слева на странице калькулятора.
Расчет длины дуги онлайн калькулятор. Геометрия круга
Часть фигуры, которая образует окружность, точки которой равноудалены, называется дугой. Если из точки центра окружности, провести лучи в точки, совпадающие с концами дуги, будет образован её центральный угол.
Если из точки центра окружности, провести лучи в точки, совпадающие с концами дуги, будет образован её центральный угол.
Определение длины дуги
Производится по следующей формуле:
где L – искомая длина дуги, π = 3,14 , r – радиус окружности, α – центральный угол.
Ответ:Длина дуги окружности равна 14,82 сантиметра.
В элементарной геометрии под дугой понимается подмножество окружности, расположенной между двумя расположенными на ней точками. На практике решать задачи по определению ее длины инженерам и архитекторам приходится достаточно часто, поскольку этот геометрический элемент широко распространен в самых разнообразных конструкциях.
Пожалуй, первым, перед кем встала эта задача, были древние зодчие, которым так или иначе приходилось определять этот параметр для сооружения сводов, широко используемых для перекрытия промежутков между опорами в круглых, многоугольных или эллиптических зданиях. Если внимательно присмотреться к дошедшим до наших дней шедеврам древнегреческого, древнеримского и особенно арабского зодчества, то можно заметить, что в их конструкциях дуги и своды встречаются чрезвычайно часто. Творения современных архитекторов ими не так богаты, но эти геометрические элементы наличествуют, конечно же, и в них.
Творения современных архитекторов ими не так богаты, но эти геометрические элементы наличествуют, конечно же, и в них.
Длину различных дуг необходимо рассчитывать при сооружении автомобильных и железных дорог, а также автодромов, причем во многих случаях от правильности и точности вычислений во многом зависит безопасность движения. Дело в том, что многие повороты магистралей с точки зрения геометрии представляют собой именно дуги, и по движению по ним на транспорт воздействуют различные физические силы. Параметры их результирующей во многом определяются длиной дуги, а также ее центральным углом и радиусом.
Конструкторам машин и механизмов приходится вычислить длины различных дуг для правильной и точной компоновки составных частей различных агрегатов. В данном случае ошибки в расчетах чреваты тем, что важные и ответственные детали будут неправильно взаимодействовать друг с другом и механизм просто не сможет функционировать так, как планируют его создатели. В качестве примеров конструкций, изобилующих такими геометрическими элементами, как дуги, можно привести двигатели внутреннего сгорания, коробки переключения передач, дерево- и металлообрабатывающее оборудование, кузовные элементы легковых и грузовых автомобилей и т. д.
д.
Дуги достаточно широко встречаются в медицине, в частности, в стоматологии. Например, они используются для исправления неправильного прикуса. Корректирующие элементы, называемые брекетами (или брекет-системами) и имеющие соответствующую форму, изготавливаются из специальных сплавов, и устанавливаются таким образом, чтобы изменить положение зубов. Само собой разумеется, что для того, чтобы лечение проходило успешно, эти дуги должны быть очень точно рассчитаны. Кроме того, дуги очень широко используются в травматологии, и, пожалуй, самым ярким примером тому является знаменитый аппарат Илизарова, изобретенный российским врачом в 1951 году и чрезвычайно успешно используемый по сей день. Неотъемлемыми его частями являются металлические дуги, снабженные отверстиями, через которые продеваются специальные спицы, и являющиеся основными опорам всей конструкции.
Круг, его части, их размеры и соотношения — вещи, с которыми ювелир постоянно сталкивается. Кольца, браслеты, касты, трубки, шары, спирали — много всего круглого приходится делать. Как же всё это посчитать, особенно если тебе посчастливилось в школе прогулять уроки геометрии?..
Как же всё это посчитать, особенно если тебе посчастливилось в школе прогулять уроки геометрии?..
Давайте сначала рассмотрим, какие у круга бывают части и как они называются.
- Окружность — линия, ограничивающая круг.
- Дуга — часть окружности.
- Радиус — отрезок, соединяющий центр круга с какой-либо точкой окружности.
- Хорда — отрезок, соединяющий две точки окружности.
- Сегмент — часть круга, ограниченная хордой и дугой.
- Сектор — часть круга, ограниченная двумя радиусами и дугой.
Интересующие нас величины и их обозначения:
Теперь посмотрим, какие задачи, связанные с частями круга, приходится решать.
- Найти длину развертки какой-либо части кольца (браслета). Задан диаметр и хорда (вариант: диаметр и центральный угол), найти длину дуги.
- Есть рисунок на плоскости, надо узнать его размер в проекции после сгибания в дугу. Заданы длина дуги и диаметр, найти длину хорды.
- Узнать высоту детали, полученной сгибанием плоской заготовки в дугу.
 Варианты исходных данных: длина дуги и диаметр, длина дуги и хорда; найти высоту сегмента.
Варианты исходных данных: длина дуги и диаметр, длина дуги и хорда; найти высоту сегмента.
Жизнь подскажет и другие примеры, а эти я привел только для того, чтобы показать необходимость задания каких-нибудь двух параметров для нахождения всех остальных. Вот этим мы и займемся. А именно, возьмем пять параметров сегмента: D, L, X, φ и H. Затем, выбирая из них все возможные пары, будем считать их исходными данными и путем мозгового штурма находить все остальные.
Чтобы зря не грузить читателя, подробных решений я приводить не буду, а приведу лишь результаты в виде формул (те случаи, где нет формального решения, я оговорю по ходу дела).
И еще одно замечание: о единицах измерения. Все величины, кроме центрального угла, измеряются в одних и тех же абстрактных единицах. Это значит, что если, к примеру, вы задаёте одну величину в миллиметрах, то другую не надо задавать в сантиметрах, а результирующие значения будут измеряться в тех же миллиметрах (а площади — в квадратных миллиметрах). То же самое можно сказать и про дюймы, футы и морские мили.
То же самое можно сказать и про дюймы, футы и морские мили.
И только центральный угол во всех случаях измеряется в градусах и ни в чём другом. Потому что, как показывает практика, люди, проектирующие что-нибудь круглое, не склонны измерять углы в радианах. Фраза «угол пи на четыре» многих ставит в тупик, тогда как «угол сорок пять градусов» — понятна всем, так как это всего на пять градусов выше нормы. Однако, во всех формулах будет присутствовать в качестве промежуточной величины еще один угол — α. По смыслу это половина центрального угла, измеренная в радианах, но в этот смысл можно спокойно не вникать.
1. Даны диаметр D и длина дуги L
; длина хорды ;
высота сегмента ; центральный угол .
2. Даны диаметр D и длина хорды X
; длина дуги ;
высота сегмента ; центральный угол .
Поскольку хорда делит круг на два сегмента, у этой задачи не одно, а два решения. Чтобы получить второе, нужно в приведенных выше формулах заменить угол α на угол .
3. Даны диаметр D и центральный угол φ
; длина дуги ;
длина хорды ; высота сегмента .
4. Даны диаметр D и высота сегмента H
; длина дуги ;
длина хорды ; центральный угол .
6. Даны длина дуги L и центральный угол φ
; диаметр ;
длина хорды ; высота сегмента .
8. Даны длина хорды X и центральный угол φ
; длина дуги ;
диаметр ; высота сегмента .
9. Даны длина хорды X и высота сегмента H
; длина дуги ;
диаметр ; центральный угол .
10. Даны центральный угол φ и высота сегмента H
; диаметр ;
длина дуги ; длина хорды .
Внимательный читатель не мог не заметить, что я пропустил два варианта:
5. Даны длина дуги L и длина хорды X
7. Даны длина дуги L и высота сегмента H
Это как раз те два неприятных случая, когда у задачи нет решения, которое можно было бы записать в виде формулы. А задача-то не такая уж редкая. Например, у вас есть плоская заготовка длины L, и вы хотите согнуть ее так, чтобы ее длина стала X (или высота стала H). Какого диаметра взять оправку (ригель)?
Какого диаметра взять оправку (ригель)?
Задача эта сводится к решению уравнений:
; — в варианте 5
; — в варианте 7
и хоть они и не решаются аналитически, зато легко решаются программным способом. И я даже знаю, где взять такую программу: на этом самом сайте, под именем . Всё то, что я тут длинно рассказываю, она делает за микросекунды.
Для полноты картины добавим к результатам наших вычислений длину окружности и три значения площадей — круга, сектора и сегмента. (Площади нам очень помогут при вычислении массы всяких круглых и полукруглых деталей, но об этом — в отдельной статье.) Все эти величины вычисляются по одним и тем же формулам:
длина окружности ;
площадь круга ;
площадь сектора ;
площадь сегмента ;
И в заключение еще раз напомню о существовании абсолютно бесплатной программы, которая выполняет все перечисленные вычисления, освобождая вас от необходимости вспоминать, что такое арктангенс и где его искать.
Сначала разберемся в отличии между кругом и окружностью. {\circ}}
{\circ}}
Диаметр, что перпендикулярен хорде, делит хорду и стянутые ею дуги пополам.
В случае, если хорды AB и CD окружности имеют пересечение в точке N , то произведения отрезков хорд, разделенные точкой N , равны между собой.
AN\cdot NB = CN \cdot ND
Касательная к окружности
Касательной к окружности принято называть прямую, у которой имеется одна общая точка с окружностью.
Если же у прямой есть две общие точки, ее называют секущей .
Если провести радиус в точку касания, он будет перпендикулярен касательной к окружности.
Проведем две касательные из этой точки к нашей окружности. Получится, что отрезки касательных сравняются один с другим, а центр окружности расположится на биссектрисе угла с вершиной в этой точке.
AC = CB
Теперь к окружности из нашей точки проведем касательную и секущую. Получим, что квадрат длины отрезка касательной будет равен произведению всего отрезка секущей на его внешнюю часть. {\circ}
{\circ}
\angle ADB = \angle AEB = \angle AFB
На одной окружности находятся вершины треугольников с тождественными углами и заданным основанием.
Угол с вершиной внутри окружности и расположенный между двумя хордами тождественен половине суммы угловых величин дуг окружности, которые заключаются внутри данного и вертикального углов.
\angle DMC = \angle ADM + \angle DAM = \frac{1}{2} \left (\cup DmC + \cup AlB \right)
Угол с вершиной вне окружности и расположенный между двумя секущими тождественен половине разности угловых величин дуг окружности, которые заключаются внутри угла.
\angle M = \angle CBD — \angle ACB = \frac{1}{2} \left (\cup DmC — \cup AlB \right)
Вписанная окружность
Вписанная окружность — это окружность, касающаяся сторон многоугольника.
В точке, где пересекаются биссектрисы углов многоугольника, располагается ее центр.
Окружность может быть вписанной не в каждый многоугольник.
Площадь многоугольника с вписанной окружностью находится по формуле:
S = pr ,
p — полупериметр многоугольника,
r — радиус вписанной окружности.
Отсюда следует, что радиус вписанной окружности равен:
r = \frac{S}{p}
Суммы длин противоположных сторон будут тождественны, если окружность вписана в выпуклый четырехугольник. И наоборот: в выпуклый четырехугольник вписывается окружность, если в нем суммы длин противоположных сторон тождественны.
AB + DC = AD + BC
В любой из треугольников возможно вписать окружность. Только одну единственную. В точке, где пересекаются биссектрисы внутренних углов фигуры, будет лежать центр этой вписанной окружности.
Радиус вписанной окружности вычисляется по формуле:
r = \frac{S}{p} ,
где p = \frac{a + b + c}{2}
Описанная окружность
Если окружность проходит через каждую вершину многоугольника, то такую окружность принято называть описанной около многоугольника . {\circ}
{\circ}
Около любого треугольника можно описать окружность, причем одну-единственную. Центр такой окружности будет расположен в точке, где пересекаются серединные перпендикуляры сторон треугольника.
Радиус описанной окружности можно вычислить по формулам:
R = \frac{a}{2 \sin A} = \frac{b}{2 \sin B} = \frac{c}{2 \sin C}
R = \frac{abc}{4 S}
a , b , c — длины сторон треугольника,
S — площадь треугольника.
Теорема Птолемея
Под конец, рассмотрим теорему Птолемея.
Теорема Птолемея гласит, что произведение диагоналей тождественно сумме произведений противоположных сторон вписанного четырехугольника.
AC \cdot BD = AB \cdot CD + BC \cdot AD
- 16.11.2014
На рисунке показана схема простого усилителя мощности класса А на транзисторах. Усилитель имеет выходную мощность порядка 20Вт на 8 Ом нагрузке. Напряжение питания может быть в пределах от 22В до 28В (4А). Источник — http://www.eleccircuit.
 com/class-a-amplifier-by-transistor/
com/class-a-amplifier-by-transistor/ - 29.09.2014
Данный усилитель предназначен для усиления мощности передатчика карманной радиостанции в диапазоне 144 МГц. При подачи на его вход сигнала мощностью 0,05Вт и питании 24В усилитель выдает мощность 5-6Вт, а при питании его напряжением 12В он выдает 3-4Вт. Входное и выходное сопротивления равны 50 Ом. Описание: первый каскад работает в классе …
- 04.10.2014
В промышленных аппаратах используют разные способы регулировки тока: шунтирование с помощью дросселей всевозможных типов, изменение магнитного потока за счет подвижности обмоток или магнитного шунтирования, применение магазинов активных балластных сопротивлений и реостатов. К недостаткам такой регулировки надо отнести сложность конструкции, громоздкость сопротивлений, их сильный нагрев при работе, неудобство при переключении. Наиболее …
- 03.10.2014
На рисунке показана схема простого преобразователя напряжения на TL496. Преобразователь преобразует постоянное напряжение 3В в постоянное напряжение 9В.
 Преобразователь напряжения весьма прост, он состоит из микросхемы TL496 и конденсатора и дросселя на 50мкГн. Выходной ток преобразователя может достигать 400мА (не гарантировано выходное напряжение 9В). Ток потребления преобразователя без нагрузки 125мкА.
Преобразователь напряжения весьма прост, он состоит из микросхемы TL496 и конденсатора и дросселя на 50мкГн. Выходной ток преобразователя может достигать 400мА (не гарантировано выходное напряжение 9В). Ток потребления преобразователя без нагрузки 125мкА.
Изначально это выглядит так:
Рисунок 463.1 . а) имеющаяся дуга, б) определение длины хорды сегмента и высоты.
Таким образом, когда имеется дуга, мы можем соединить ее концы и получим хорду длиной L. Посредине хорды мы можем провести линию, перпендикулярную хорде и таким образом получим высоту сегмента H. Теперь, зная длину хорды и высоту сегмента, мы можем сначала определить центральный угол α, т.е. угол между радиусами, проведенными из начала и конца сегмента (на рисунке 463.1 не показаны), а затем и радиус окружности.
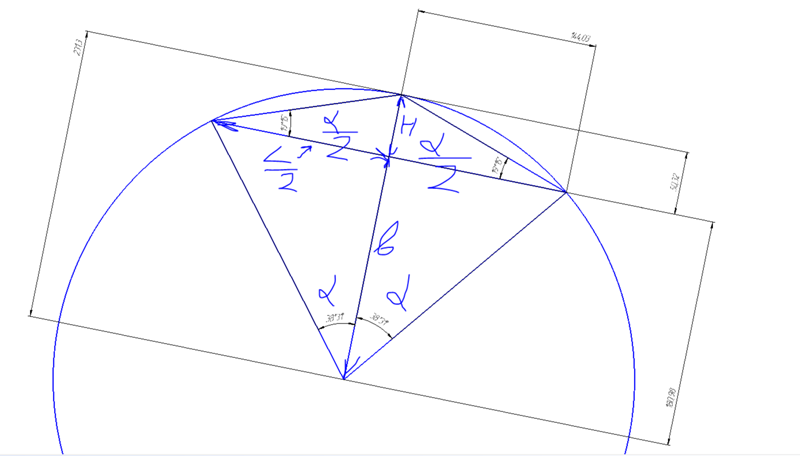
Решение подобной задачи достаточно подробно рассматривалось в статье «Расчет арочной перемычки «, поэтому здесь лишь приведу основные формулы:
tg(a /4) = 2Н/L (278. 1.2)
1.2)
а /4 = arctg(2H/L )
R = H /(1 — cos(a /2)) (278.1.3)
Как видим, с точки зрения математики никаких проблем с определением радиуса окружности нет. Данный метод позволяет определить значение радиуса дуги с любой возможной точностью. Это главное достоинство данного метода.
А теперь поговорим о недостатках.
Проблема данного метода даже не в том, что требуется помнить формулы из школьного курса геометрии, успешно забытые много лет назад — для того, чтобы напомнить формулы — есть интернет. А вот калькулятор с функцией arctg, arcsin и проч. есть далеко не у каждого пользователя. И хотя эту проблему также успешно позволяет решить интернет, но при этом не следует забывать, что мы решаем достаточно прикладную задачу. Т.е. далеко не всегда нужно определить радиус окружности с точностью до 0.0001 мм, точность 1 мм может быть вполне приемлема.
Кроме того, для того, чтобы найти центр окружности, нужно продлить высоту сегмента и отложить на этой прямой расстояние, равное радиусу.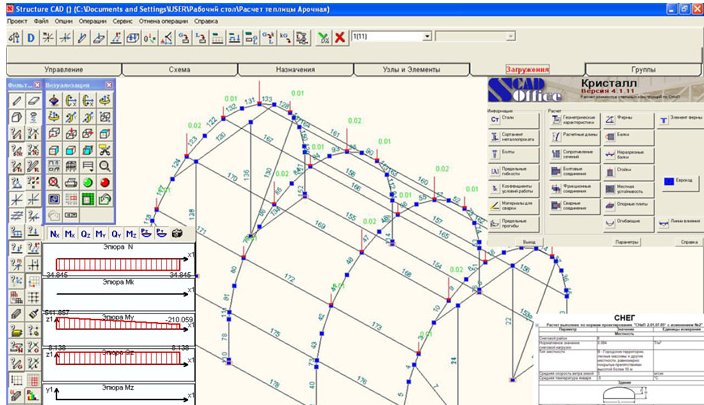 Так как на практике мы имеем дело с не идеальными измерительными приборами, к этому следует прибавить возможную погрешность при разметке, то получается, что чем меньше высота сегмента по отношению к длине хорды, тем больше может набежать погрешность при определении центра дуги.
Так как на практике мы имеем дело с не идеальными измерительными приборами, к этому следует прибавить возможную погрешность при разметке, то получается, что чем меньше высота сегмента по отношению к длине хорды, тем больше может набежать погрешность при определении центра дуги.
Опять же не следует забывать о том, что мы рассматриваем не идеальный случай, т.е. это мы так сходу назвали кривую дугой. В действительности это может быть кривая, описываемая достаточно сложной математической зависимостью. А потому найденный таким образом радиус и центр окружности могут и не совпадать с фактическим центром.
В связи с этим я хочу предложить еще один способ определения радиуса окружности, которым сам часто пользуюсь, потому что этим способом определить радиус окружности намного быстрее и проще, хотя точность при этом значительно меньше.
Второй метод определения радиуса дуги (метод последовательных приближений)
Итак продолжим рассмотрение имеющейся ситуации.
Так как нам все равно необходимо найти центр окружности, то для начала мы из точек, соответствующих началу и концу дуги, проведем как минимум две дуги произвольного радиуса.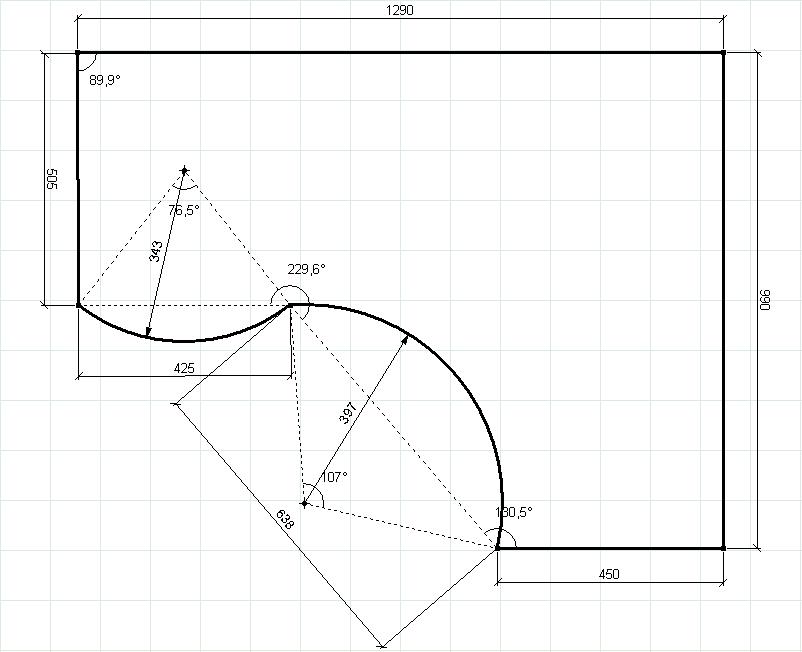 Через пересечение этих дуг будет проходить прямая, на которой и находится центр искомой окружности.
Через пересечение этих дуг будет проходить прямая, на которой и находится центр искомой окружности.
Теперь нужно соединить пересечение дуг с серединой хорды. Впрочем, если мы из указанных точек проведем не по одной дуге, а по две, то данная прямая будет проходить через пересечение этих дуг и тогда искать середину хорды вовсе не обязательно.
Если расстояние от пересечения дуг до начала или конца рассматриваемой дуги больше, чем расстояние от пересечения дуг до точки, соответствующей высоте сегмента, то значит центр рассматриваемой дуги находится ниже на прямой, проведенной через пересечение дуг и середину хорды. Если меньше — то искомый центр дуги выше на прямой.
Исходя из этого на прямой принимается следующая точка, предположительно соответствующая центру дуги, и от нее производятся те же измерения. Затем принимается следующая точка и измерения повторяются. С каждой новой точкой разница измерений будет все меньше.
Вот собственно и все. Не смотря на столь пространное и мудреное описание, для определения радиуса дуги таким способом с точностью до 1 мм достаточно 1-2 минут.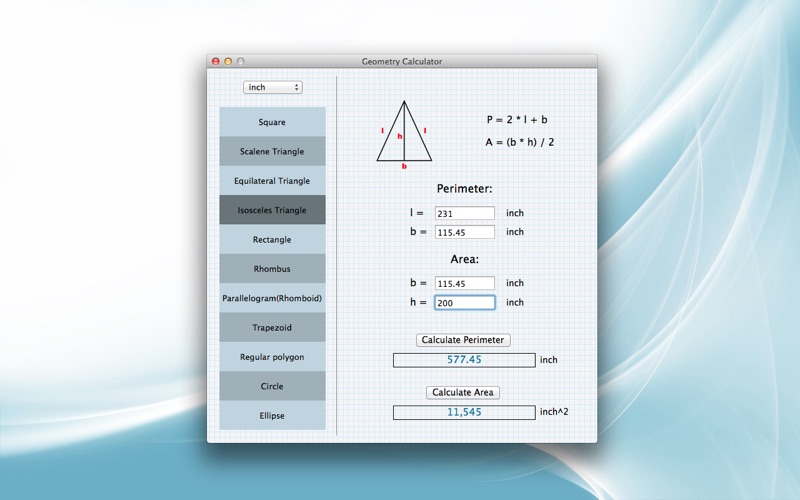
Теоретически это выглядит примерно так:
Рисунок 463.2 . Определение центра дуги методом последовательных приближений.
А на практике примерно так:
Фотография 463.1 . Разметка заготовки сложной формы с разными радиусами.
Тут только добавлю, что иногда приходится находить и чертить несколько радиусов, потому на фотографии так много всего и намешано.
Расчет арки онлайн калькулятор. Параметрическое уравнение циклоиды и уравнение в декартовых координатах Длина дуги одной арки циклоиды
ЛЕМНИСКАТЫ
Уравнение в полярных координатах:
r 2 = a 2 cos2θ
(x 2 + y 2) 2 = a 2 (x 2 — y 2)
Угол между AB» или A»B и осью x = 45 o
Площадь одной петли = a 2 /2
ЦИКЛОИДА
Площадь одной дуги = 3πa 2
Длина дуги одной арки = 8a
Это кривая, описываемая точкой Р на окружности радиусом а, которая катится вдоль оси х.
ГИПОЦИКЛОИДЫ С ЧЕТЫРЬМЯ ОСТРИЯМИ
Уравнение в прямоугольных координатах:
x 2/3 + y 2/3 = a 2/3
Уравнения в параметрической форме:
Площадь, ограниченная кривой = 3πa 2 /8
Длина дуги целой кривой = 6a
Это кривая, описываемая точкой Р на окружности радиусом a/4, которая катится внутри окружности радиусом a.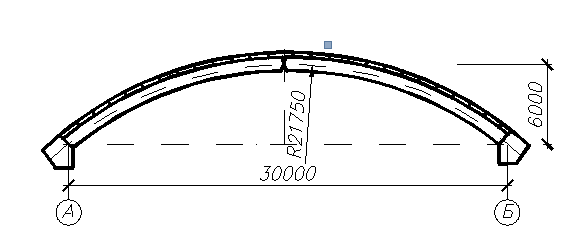
КАРДИОИДА
Уравнение: r = a(1 + cosθ)
Площадь, ограниченная кривой = 3πa 2 /2
Длина дуги кривой = 8a
Это кривая, описываемая точкой Р на окружности радиусом a, которая катится снаружи окружности радиусом a. Эта кривая также является частным случаем улитки Паскаля.
ЦЕПНАЯ ЛИНИЯ
Уравнение:
y = a(e x/a + e -x/a)/2 = acosh(x/a)
Это кривая, по которой бы повисла цепь, подвешенная вертикально от точки А к В.
ТРЕХЛЕПЕСТКОВАЯ РОЗА
Уравнение: r = acos3θ
Уравнение r = acos3θ подобно кривой, полученной вращением против часовой стрелки по кривой 30 o или π/6 радиан.
В общем, r = acosnθ или r = asinnθ имеет n лепестков если n является нечетным.
ЧЕТЫРЕХЛЕПЕСТКОВАЯ РОЗА
Уравнение: r = acos2θ
Уравнение r = asin2θ подобно кривой, полученной вращением против часовой стрелки по кривой 45 o или π/4 радиан.
В общем r = acosnθ или r = asinnθ имеет 2n лепестков если n — четное.
ЭПИЦИКЛОИДА
Параметрические уравнения:
Это кривая, описываемая точкой Р на окружности радиуса b, когда она катится по внешней стороне окружности радиусом а. Кардиоида является частным случаем эпициклоиды.
ОБЩАЯ ГИПОЦИКЛОИДА
Параметрические уравнения:
Это кривая, описываемая точкой Р на окружности радиуса b, когда она катится по внешней стороне окружности радиусом а.
Если b = a/4, кривая является гипоциклоидой с четырьмя остриями.
ТРОХОИДА
Параметрические уравнения:
Это кривая, описываемая точкой Р на дистанции b от центра окружности с радиусом а, когда она катится по оси x.
Если b укороченной циклоидой.
Если b > a, кривая имеет форму, показанную на рис. 11-11 и называется троходой.
Если b = a, кривая есть циклоидой.
ТРАКТРИСА
Параметрические уравнения:
Это кривая, описываемая конечной точкой Р натянутой струны длиной PQ, когда другой конец Q перемещается вдоль оси х.
ВЕРЗЬЕРА (ВЕРЗИЕРА) АНЬЕЗИ (ИНОГДА ЛОКОН АНЬЕЗИ)
Уравнение в прямоугольных координатах: y = 8a 3 /(x 2 + 4a 2)
Параметрические уравнения:
В. На рисунке переменная линия OA пересекающая y = 2a и круг с радиусом a с центром (0,a) в A и B соотвественно. Любая точка P на «локоне» определяется построением линий, параллельных к осям x и y, и через B и A соответственно и определяющие точку пересечения P.
ДЕКАРТОВ ЛИСТ
Уравнение в прямоугольных координатах:
x 3 + y 3 = 3axy
Параметрические уравнения:
Площадь петли 3a 2 /2
Уравнение асимптоты: x + y + a = 0.
ЭВОЛЬВЕНТА ОКРУЖНОСТИ
Параметрические уравнения:
Эта кривая, описанная конечной точкой P струны, когда она разматывается с круга с радиусом a.
ЭВОЛЬВЕНТА ЭЛЛИПСА
Уравнение в прямоугольных координатах:
(ax) 2/3 + (by) 2/3 = (a 2 — b 2) 2/3
Параметрические уравнения:
Эта кривая является огибающей нормалью к эллипсу x 2 /a 2 + y 2 /b 2 = 1.
ОВАЛЫ КАССИНИ
Полярное уравнение: r 4 + a 4 — 2a 2 r 2 cos2θ = b 4 .
Это кривая, описываемая такой точкой P, что произведение ее расстояния от двух фиксированных точек [ расстояние 2a в сторону] есть постоянной b 2 .
Кривая, как на фигурах внизу, когда b a соответственно.
Если b = a, кривая есть лемниската
УЛИТКА ПАСКАЛЯ
Полярное уравнение: r = b + acosθ
Пусть OQ будет линией, соединяющей центр O с любой точкой Q на окружности диаметром a проходящей через O. Тогда кривая есть фокусом всех точек P, таких, что PQ = b.
Кривая, показанная на рисунках внизу когда b > a или b
ЦИССОИДА ДИОКЛА
Уравнение в прямоугольных координатах: y 2 = x 3 /(2a — x)
Параметрические уравнения:
Это кривая, описываемая такой точкой P, что расстояние OP = расстоянию RS. Используется в задаче удвоения куба , т.e. нахождения стороны куба, который имеет удвоенный объем заданного куба
СПИРАЛЬ АРХИМЕДА
Полярное уравнение: r = aθ
Длина дуги циклоиды впервые была вычислена английским архитектором и математиком Реном в 1658 году. Рен исходил из механических соображений, напоминающих первые работы Торричелли и Роберваля. Он рассматривал поворот катящегося круга на весьма малый угол около «нижней» точки производящей окружности. Чтобы придать наводящим соображениям Рена доказательную силу, пришлось бы рассмотреть целый ряд вспомогательных теорем, соответственно пришлось бы затратить слишком много труда.
Рен исходил из механических соображений, напоминающих первые работы Торричелли и Роберваля. Он рассматривал поворот катящегося круга на весьма малый угол около «нижней» точки производящей окружности. Чтобы придать наводящим соображениям Рена доказательную силу, пришлось бы рассмотреть целый ряд вспомогательных теорем, соответственно пришлось бы затратить слишком много труда.
Гораздо удобнее воспользоваться более длинным, но пологим путем. Для этого нужно рассмотреть особую кривую, которая есть у каждой пологой кривой — ее развёрткой.
Рассмотрим выпуклую дугу АВ кривой линии (рис. 4.1). Представим себе, что к дуге АВ в точке А прикреплена гибкая нерастяжимая нить такой же длины, как сама дуга АВ, причем эта нить «навёрнута» на кривую и плотно к ней прилегает, так что её конец совпадает с точкой В. Будем «развертывать» — распрямлять нить, держа ее натянутой, так что свободная часть СМ нити будет все время направлена по касательной к дуге АВ. При этих условиях конец нити опишет некоторую кривую.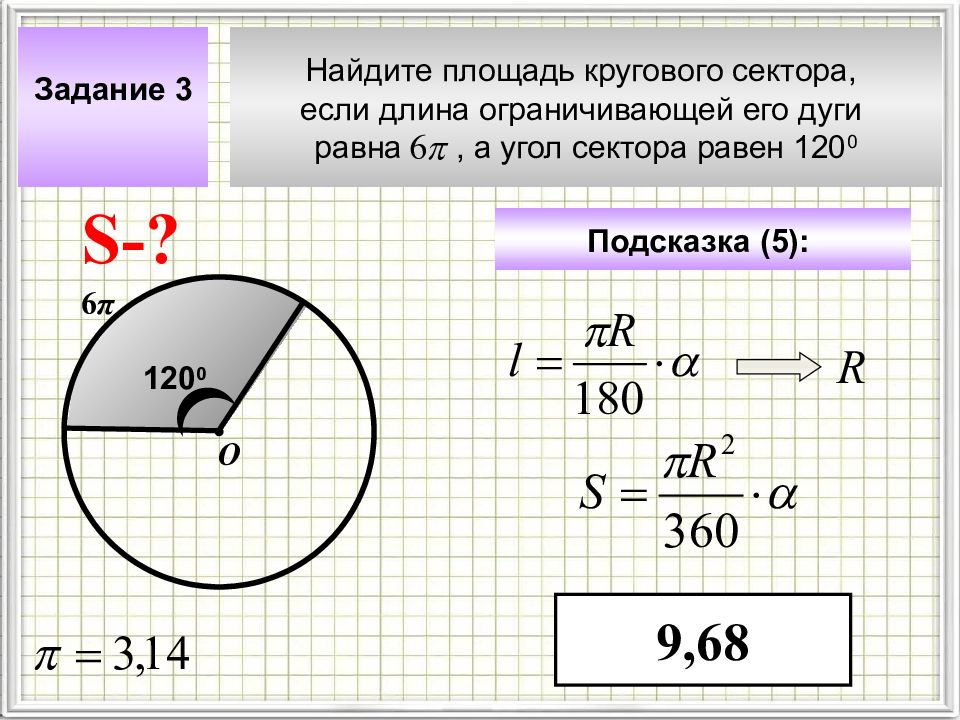 Вот эта-то кривая и называется разверткой или, по-латыни, эвольвентой исходной кривой.
Вот эта-то кривая и называется разверткой или, по-латыни, эвольвентой исходной кривой.
Если дуга кривой не всюду выпукла в одну сторону, если она, подобно кривой АВ на рис. 4.2, имеет точку С, в которой касательная к кривой переходит с одной ее стороны на другую (такая точка называется точкой перегиба), то и в этом случае можно говорить о развертке кривой, но рассуждения придется немного усложнить.
Представим себе, что нить закреплена как раз в точке перегиба С (рис. 4.2). Нить, сматываясь с дуги ВС, опишет кривую ВМР — развертку.
Теперь представим себе нить, намотанную на дугу АС исходной кривой, но эта нить уже удлиненная: в точке С к ней привязан кусочек нити СР. Сматывая удлиненную нить АСР с кривой СА, мы получим дугу РНК, образующую вместе с дугой ВМР единую непрерывную кривую — непрерывную, но не везде плавную: точке прогиба С исходной кривой будет соответствовать острие (точка возврата) кривой ВМРНК: кривая ВМРНК и будет эвольвентой (разверткой) кривой ВСА.
Эти примеры помогли нам привыкнуть к новым понятиям эволюты и эвольвенты. Теперь займёмся исследованием разверток циклоидальных кривых.
Изучая ту или иную кривую, мы нередко строили вспомогательную кривую — «спутницу» данной кривой. Так, мы стоили синусоиду — спутницу циклоиды. Теперь, исходя из данной циклоиды, мы постоим неразрывно связанную с ней вспомогательную циклоиду же. Оказывается, совместное изучение такой пары циклоид в некоторых отношениях проще, чем изучение одной отдельно взятой циклоиды. Такую вспомогательную циклоиду мы будем называть сопровождающей циклоидой.
Рассмотрим половину арки циклоиды АМВ (рис. 4.3). Нас не должно смущать, что циклоида эта расположена непривычным образом («вверх ногами»). Проведем 4 прямые, параллельные направляющей прямой АК на расстояниях a , 2a , 3a и 4a . Построим производящий круг в положении, соответствующем точке М (на рис. 4.3 центр этого круга обозначен буквою О). Угол поворота МОН обозначим через ц. Тогда отрезок АН будет равен бц (угол ц выражен в радианах).
Тогда отрезок АН будет равен бц (угол ц выражен в радианах).
Диаметр НТ производящего круга продолжим за точку Т до пересечения (в точке Е) с прямой РР. На ТЕ как на диаметре построим окружность (с центром О 1). Построим касательную в точке М к циклоиде АМВ. Для этого точку М нужно, как мы знаем, соединить с точкой Т. Продолжим касательную МТ за точку Т до пересечения со вспомогательной окружностью, и точку пересечения назовем М 1 . Вот этой-то точкой М 1 мы и хотим теперь заняться.
Угол МОН мы обозначили через ц. Поэтому угол МТН будет равняться (вписанный угол, опирающийся на ту же дугу). Треугольник ТО 1 М 1 , очевидно, равнобедренный. Поэтому не только угол О 1 ТМ 1 , но и угол ТМ 1 О 1 будут каждый равняться. Таким образом, на долю угла ТО 1 М 1 в треугольнике ТО 1 М 1 остается ровно р — ц радианов (вспомним, что угол 180? равен р радианов). Заметим еще, что отрезок НК равен, очевидно, б (р — ц).
Рассмотрим теперь окружности с центром О 2 , изображенную на рис. 4.3 штриховой линией. Из чертежа ясно, чтом это за окружность. Если катить ее без скольжения по прямой СВ, то её точка В опишет циклоиду ВВ. Когда штриховой круг повернется на угол р — ц, центр О 2 придет в точку О 1 , а радиус О 2 В займет положение О 1 М 1 . Таким образом, построенная нами точка М 1 оказывается точкою циклоиды ВВ.
4.3 штриховой линией. Из чертежа ясно, чтом это за окружность. Если катить ее без скольжения по прямой СВ, то её точка В опишет циклоиду ВВ. Когда штриховой круг повернется на угол р — ц, центр О 2 придет в точку О 1 , а радиус О 2 В займет положение О 1 М 1 . Таким образом, построенная нами точка М 1 оказывается точкою циклоиды ВВ.
Описанное построение ставит в соответствие каждой точке М циклоиды АМВ точку М 1 циклоиды ВМ 1 В. На рис. 4.4 это соответствие показано более наглядно. Полученная таким путем циклоида называется сопровождающей. На рис. 4.3 и 4.4 циклоиды, изображенные жирными штриховыми линиями, являются сопровождающими по отношению к циклоидам, изображенными жирными сплошными линиями.
Из рис. 4.3 видно, что прямая ММ 1 является нормалью в точке М 1 к сопровождающей циклоиде. Действительно, эта прямая проходит через точку М 1 циклоиды и через точку Т касания производящего круга и направляющей прямой («наинизшую» точку производящего круга, как мы говорили когда-то; теперь она оказалась «наивысшей», потому что чертеж повернут). Но эта же прямая, по построению, является касательной к «основанию» циклоиде АМВ. Таким образом, исходная циклоида касается каждой нормали сопровождающей циклоиды. Она является огибающей для нормалей сопровождающей циклоиды, т.е. ее эволютой. А «сопровождающая» циклоида оказывается просто-напросто эвольвентой исходной циклоиды!
Но эта же прямая, по построению, является касательной к «основанию» циклоиде АМВ. Таким образом, исходная циклоида касается каждой нормали сопровождающей циклоиды. Она является огибающей для нормалей сопровождающей циклоиды, т.е. ее эволютой. А «сопровождающая» циклоида оказывается просто-напросто эвольвентой исходной циклоиды!
Занимаясь этим громоздким, но в сущности простым построением, мы доказали замечательную теорему, открытую голландским ученым Гюйгенсом. Вот эта теорема: эволютой циклоиды служит точно такая же циклоида, только сдвинутая .
Построив эволюту не к одной арке, а ко всей циклоиде (что можно, разумеется, сделать только мысленно), затем эволюту к этой эволюте и т.д., получим рис. 4.5, напоминающий черепицу.
Обратим внимание на то, что при доказательстве теоремы Гюйгенса мы не пользовались ни бесконечно малыми, ни неделимыми, ни приблизительными оценками. Даже механикой мы не пользовались, хотя употребляли иногда заимствованные из механики выражения. Доказательство это совершенно в духе тех рассуждений, которыми пользовались ученые XVII века, когда хотели строго обосновать результаты, полученные с помощью различных наводящих соображений.
Доказательство это совершенно в духе тех рассуждений, которыми пользовались ученые XVII века, когда хотели строго обосновать результаты, полученные с помощью различных наводящих соображений.
Из теоремы Гюйгенса получается сразу важное следствие. Рассмотрим отрезок АВ на рис. 4.4. Длина этого отрезка равна, очевидно, 4a . Представим себе теперь, что на дугу АМВ циклоиды намотана нить, закрепленная в точке А и снабженная карандашом в точке В. Если мы будем «сматывать» нить, то карандаш будет двигаться по развертке циклоиды АМВ, т.е. по циклоиде ВМ 1 В. Длина нити, равная длине полуарки циклоиды, будет, очевидно, равна отрезку АВ, т.е., как мы видели, 4a . Следовательно, длина L всей арки циклоиды будет равна 8a , и формулу L=8a можно считать теперь достаточно строго доказанной.
Вычислим длину дуги при помощи дифференциальной геометрии. Решение, полученное таким способом получится куда короче и легче:
где t?
| r(t)| ===2sin
5.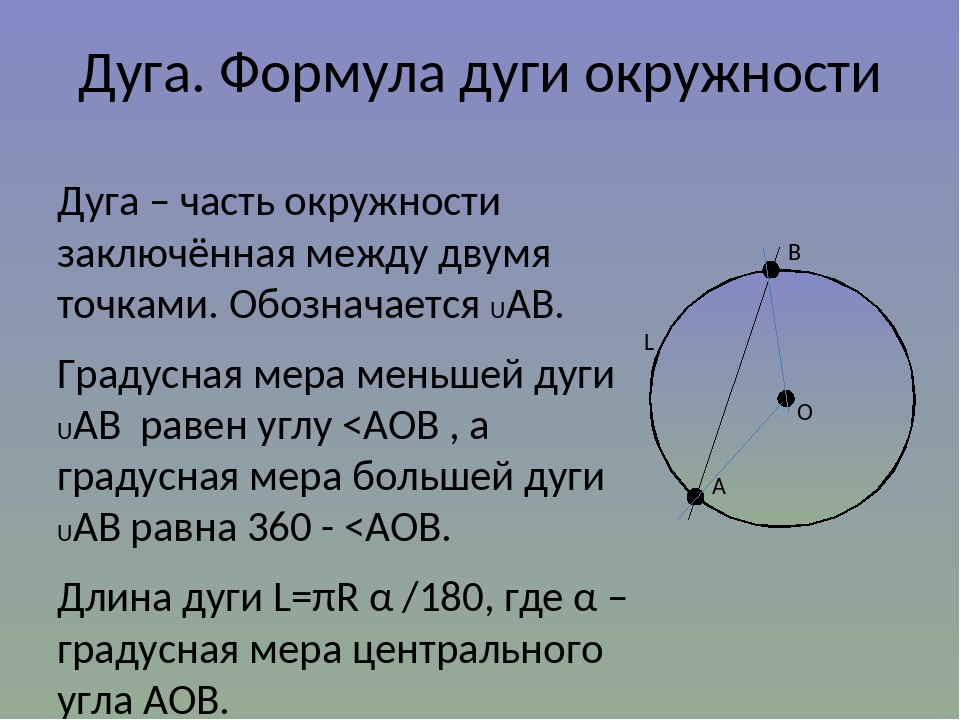 Параметрическое уравнение циклоиды и уравнение в декартовых координатах
Параметрическое уравнение циклоиды и уравнение в декартовых координатах
Допустим, что у нас дана циклоида, образованная окружностью радиуса а с центром в точке А.
Если выбрать в качестве параметра, определяющего положение точки, угол t=∟NDM на который успел повернуться радиус, имевший в начале качения вертикально е положение АО, то координаты х и у точки М выразятся следующим образом:
х= OF = ON — NF = NM — MG = at-a sin t,
y= FM = NG = ND – GD = a – a cos t
Итак параметрические уравнения циклоиды имеют вид:
При изменении t от -∞ до +∞ получится кривая, состоящая из бесчисленного множества таких ветвей, какая изображена на данном рисунке.
Так же, помимо параметрического уравнения циклоиды, существует и ее уравнение в декартовых координатах:
Где r – радиус окружности, образующей циклоиду.
6. Задачи на нахождение частей циклоиды и фигур, образованных циклоидой
Задача №1. Найти площадь фигуры, ограниченной одной аркой циклоиды, уравнение которой задано параметрически
и осью Ох.
Решение. Для решения данной задачи, воспользуемся известными нам фактами из теории интегралов, а именно:
Площадь криволинейного сектора.
Рассмотрим некоторую функцию r = r(ϕ), определенную на [α, β].
ϕ 0 ∈ [α, β] соответствует r 0 = r(ϕ 0) и, значит, точка M 0 (ϕ 0 , r 0), где ϕ 0 ,
r 0 — полярные координаты точки. Если ϕ будет меняться, «пробегая» весь[α, β], то переменная точка M опишет некоторую кривую AB, заданную
уравнением r = r(ϕ).
Определение 7.4. Криволинейным сектором называется фигура, ограниченная двумя лучами ϕ = α, ϕ = β и кривой AB, заданной в полярных
координатах уравнением r = r(ϕ), α ≤ ϕ ≤ β.
Справедлива следующая
Теорема. Если функция r(ϕ) > 0 и непрерывна на [α, β], то площадь
криволинейного сектора вычисляется по формуле:
Эта теорема была доказана ранее в теме определенного интеграла.
Исходя из приведенной выше теоремы, наша задача о нахождении площади фигуры, ограниченной одной аркой циклоиды, уравнение которой задано параметрические x= a (t – sin t) , y= a (1 – cos t) , и осью Ох, сводится к следующему решению.
Решение. Из уравнения кривой dx = a(1−cos t) dt. Первая арка циклоиды соответствует изменению параметра t от 0 до 2π. Следовательно,
Задача №2. Найти длину одной арки циклоиды
Так же в интегральном исчислении изучалась следующая теорема и следствие из нее.
Теорема. Если кривая AB задана уравнением y = f(x), где f(x) и f ’ (x) непрерывны на , то AB является спрямляемой и
Следствие. Пусть AB задана параметрически
L AB = (1)
Пусть функции x(t), y(t) непрерывно-дифференцируемые на [α, β]. Тогда
формулу (1) можно записать так
Сделаем замену переменных в этом интеграле x = x(t), тогда y’(x)= ;
dx= x’(t)dt и, следовательно:
А теперь вернемся к решении нашей задачи.
Решение. Имеем , а поэтому
Задача №3. Надо найти площадь поверхности S, образованной от вращения одной арки циклоиды
L={(x,y): x=a(t – sin t), y=a(1 – cost), 0≤ t ≤ 2π}
В интегральном исчислении существует следующая формула для нахождения площади поверхности тела вращения вокруг оси х кривой, заданной на отрезке параметрически: x=φ(t), y=ψ(t) (t 0 ≤t ≤t 1)
Применяя эту формулу для нашего уравнения циклоиды получаем:
Задача №4. Найти объем тела, полученного при вращении арки циклоиды
Найти объем тела, полученного при вращении арки циклоиды
Вдоль оси Ох.
В интегральном исчислении при изучении объемов есть следующее замечание:
Если кривая, ограничивающая криволинейную трапецию задана параметрическими уравнениями и функции в этих уравнениях удовлетворяют условиям теоремы о замене переменной в определенном интеграле, то объем тела вращения трапеции вокруг оси Ох, будет вычисляться по формуле
Воспользуемся этой формулой для нахождения нужного нам объема.
Задача решена.
Заключение
Итак, в ходе выполнения данной работы были выяснены основные свойства циклоиды. Так же научились строить циклоиду, выяснила геометрический смысл циклоиды. Как оказалось циклоида имеет огромное практическое применение не только в математике, но и в технологических расчетах, в физике. Но у циклоиды есть и другие заслуги. Ею пользовались ученые XVII века при разработке приемов исследования кривых линий, — тех приемов, которые привели в конце концов к изобретению дифференциального и интегрального исчислений. Она же была одним из «пробных камней», на которых Ньютон, Лейбниц и их первые исследователи испытывали силу новых мощных математических методов. Наконец, задача о брахистохроне привела к изобретению вариационного исчисления, столь нужного физикам сегодняшнего дня. Таким образом, циклоида оказалась неразрывно связанной с одним из самых интересных периодов в истории математики.
Она же была одним из «пробных камней», на которых Ньютон, Лейбниц и их первые исследователи испытывали силу новых мощных математических методов. Наконец, задача о брахистохроне привела к изобретению вариационного исчисления, столь нужного физикам сегодняшнего дня. Таким образом, циклоида оказалась неразрывно связанной с одним из самых интересных периодов в истории математики.
Литература
1. Берман Г.Н. Циклоида. – М., 1980
2. Веров С.Г. Брахистохрона, или еще одна тайна циклоиды // Квант. – 1975. — №5
3. Веров С.Г. Тайны циклоиды// Квант. – 1975. — №8.
4. Гаврилова Р.М., Говорухина А.А., Карташева Л.В., Костецкая Г.С.,Радченко Т.Н. Приложения определенного интеграла. Методические указания и индивидуальные задания для студентов 1 курса физического факультета. — Ростов н/Д: УПЛ РГУ, 1994.
5. Гиндикин С.Г. Звездный век циклоиды // Квант. – 1985. — №6.
6. Фихтенгольц Г.М. Курс дифференциального и интегрального исчисления. Т.1. – М.,1969
Такая линия и называется «огибающей». Всякая кривая линия есть огибающая своих касательных.
Всякая кривая линия есть огибающая своих касательных.
Материя и движение, и тот метод, который они составляют, дают возможность каждому реализовать свои потенциальные возможности в познании истины. Разработка методики развития диалектико-материалистической формы мышления и овладение аналогичным ему методом познания является вторым шагом на пути решения проблемы развития и реализации возможностей Человека. Фрагмент XX Возможности…
Обстановке могут заболеть неврастенией – неврозом, основу клинической картины которого составляет астеническое состояние. И в случае неврастении, и в случае декомпенсации неврастенической психопатии существо душевной (психологической) защиты сказывается уходом от трудностей в раздражительную слабость с вегетативными дисфункциями: либо от нападения человек бессознательно «отбивается»больше…
Различных видах деятельности; развитии пространственного воображения и пространственных представлений, образного, пространственного, логического, абстрактного мышления школьников; формировании умений применять геометро-графические знания и умения для решения различных прикладных задач; ознакомлении с содержанием и последовательностью этапов проектной деятельности в области технического и. ..
..
Дуги. Спиралями являются также эвольвенты замкнутых кривых, например эвольвента окружности. Названия некоторым спиралям даны по сходству их полярных уравнений с уравнениями кривых в декартовых координатах, например: · параболическая спираль (а — r)2 = bj, · гиперболическая спираль: r = а/j. · Жезл: r2 = a/j · si-ci-cпираль, параметрические уравнения которой имеют вид: , }
Калькулятор длины дуги
Этот калькулятор длины дуги — инструмент, который может вычислить длину дуги и площадь сектора круга. В этой статье подробно объясняется формула длины дуги и даются пошаговые инструкции по ее определению. Вы также узнаете уравнение для площади сектора.
Формула длины дуги
Длина дуги зависит от радиуса окружности и центрального угла θ . Мы знаем, что для угла, равного 360 градусам (2π), длина дуги равна длине окружности.Следовательно, поскольку соотношение между углом и длиной дуги постоянное, мы можем сказать, что:
L / θ = C / 2π По окружности C = 2πr ,
L / θ = 2πr / 2π л / θ = г Мы находим формулу длины дуги, умножая это уравнение на θ:
L = г * θ Следовательно, длина дуги равна радиусу, умноженному на центральный угол (в радианах).
Площадь сектора круга
Аналогичным образом мы можем найти площадь сектора круга.Мы знаем, что площадь всего круга равна πr². Из пропорций,
А / θ = πr² / 2π А / θ = r² / 2 Формула площади сектора:
A = r² * θ / 2 Как найти длину дуги и площадь сектора: пример
- Определитесь с радиусом вашего круга. Например, он может быть равен 15 см. (Вместо этого вы также можете ввести диаметр в калькулятор длины дуги.)
- Какой будет угол между концами дуги? Скажем, он равен 45 градусам или π / 4.
- Рассчитайте длину дуги по приведенной выше формуле:
L = r * θ = 15 * π / 4 = 11,78 см. - Рассчитайте площадь сектора:
A = r² * θ / 2 = 15² * π / 4/2 = 88,36 см². - Вы также можете использовать калькулятор длины дуги, чтобы найти центральный угол или радиус окружности. Просто введите любые два значения в соответствующие поля и наблюдайте, как он выполняет все расчеты за вас.

Обязательно ознакомьтесь с уравнением калькулятора круга!
Как найти длину дуги без радиуса?
Чтобы рассчитать длину дуги без радиуса, нужен центральный угол и площадь сектора :
- Умножьте площадь на 2 и разделите результат на центральный угол в радианах.
- Найдите квадратный корень из этого деления.
- Умножьте этот корень еще раз на центральный угол, чтобы получить длину дуги.
- Единицы будут квадратным корнем из единиц площади сектора.
Или центральный угол и длина хорды :
- Разделите центральный угол в радианах на 2 и выполните для него синусоидальную функцию.
- Разделите длину хорды на удвоение результата шага 1. Этот расчет дает вам радиус.
- Умножьте радиус на центральный угол, чтобы получить длину дуги.
Как рассчитать длину дуги без угла?
Чтобы рассчитать длину дуги без угла, вам нужны радиус и площадь сектора :
- Умножьте площадь на 2.

- Затем разделите результат на квадрат радиуса (убедитесь, что единицы измерения совпадают), чтобы получить центральный угол в радианах.
Или вы можете использовать радиус и длину хорды :
- Разделите длину пояса на двойной радиус.
- Найдите обратный синус результата.
- Удвойте результат обратного синуса, чтобы получить центральный угол в радианах.
- Когда у вас есть центральный угол в радианах, умножьте его на радиус, чтобы получить длину дуги.
Обязательно ли указывать длину дуги в радианах?
Длина дуги — это расстояние, поэтому она не может быть в радианах. Однако центральный угол не обязательно должен быть в радианах. Он может быть в любых единицах измерения для углов, от градусов до угловых секунд. Использование в радианах, однако, намного проще для вычислений относительно длины дуги, поскольку найти его так же просто, как умножить угол на радиус.
Онлайн калькулятор: Круговой сегмент
Круговой сегментКруговой сегмент — это участок окружности, «отрезанной» от остальной части окружности секущей (хордой).
На фото:
L — длина дуги
h — высота
c — пояс
R — радиус
a — угол
Если вы знаете радиус и угол, вы можете использовать следующие формулы для расчета остальных параметров сегмента:
Формулы круговых сегментов
Площадь:
[1]
Длина дуги:
Длина хорды:
Высота сегмента:
Круговой сегмент
Точность вычисленияЦифры после десятичной точки: 2
content_copy Ссылка сохранить Сохранить расширение Виджет
Но если вы не знаете радиус и угол, вы все равно можете рассчитать параметры сегмента по длине хорды и высоте сегмента:
Сегмент, определяемый хордой и высотой
Точность вычисленияЦифры после десятичной точки: 2
content_copy Ссылка сохранить Сохранить расширение Виджет
Формула радиуса сегмента по хорде и высоте:
Затем вы можете рассчитать угол сегмента по следующей формуле:
Вы также можете использовать следующий калькулятор, чтобы получить площадь сегмента по его радиусу и высоте:
Площадь сегмента круга по радиусу и высоте
Точность вычисленияЦифры после десятичной точки: 2
content_copy Ссылка сохранить Сохранить расширение Виджет
Этот калькулятор вычисляет угол по следующей формуле:
, затем он использует формулу [1] для вычисления площади сегмента.
15 расчетов круговых сегментов в одной программе
Калькулятор ниже включает в себя все возможные расчеты, касающиеся параметров кругового сегмента:
- длина дуги
- угол, хорда
- высота
- радиус
- площадь
Выберите любые два аргумента, все остальное калькулятор выдаст.
Круговой сегмент — полное решение
Угол в градусахДлина дугиAreaChordHeightRadius Угол в градусахДлина дугиAreaChordHeightRadiusТочность вычисленияЦифры после десятичной точки: 2
Файл очень большой.Во время загрузки и создания может произойти замедление работы браузера.
Скачать закрыть
content_copy Ссылка сохранить Сохранить расширение Виджет
Калькулятор длины дуги | Pi Day
Чтобы использовать калькулятор длины дуги, просто введите центральный угол и радиус в два верхних поля. Если нам дан только диаметр, а не радиус, мы можем ввести его вместо этого, хотя радиус всегда равен половине диаметра, поэтому его не так сложно вычислить.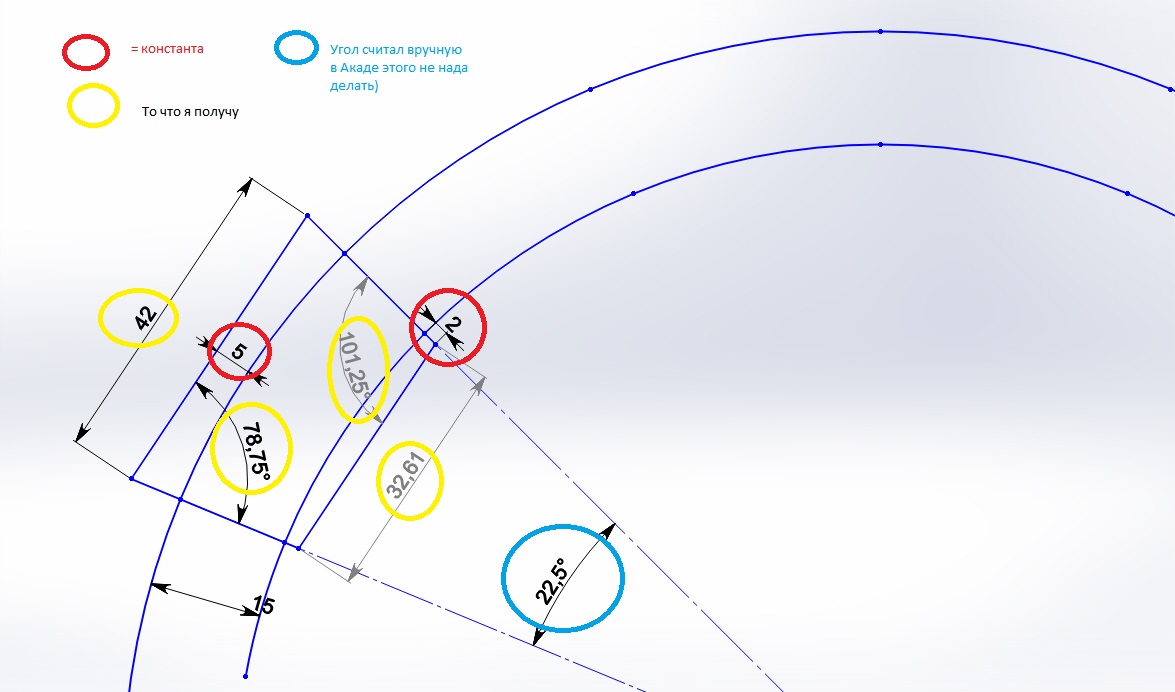
Калькулятор определит длину дуги . Он также рассчитает площадь сектора с тем же центральным углом.
Как рассчитать площадь сектора и длину дугиНаши калькуляторы очень удобны, но мы можем найти длину дуги и площадь сектора вручную. Хорошая практика — убедиться, что вы умеете рассчитывать эти измерения самостоятельно.
Как найти длину дугиДлина дуги — это лишь часть длины окружности всей окружности.Итак, нам нужно найти долю круга, образованного известным нам центральным углом, а затем найти окружности всей окружности, образованной известным нам радиусом. Затем мы просто умножаем их вместе. Давайте попробуем пример, где центральный угол равен 72 °, а радиус — 3 метра.
Во-первых, давайте найдем долю окружности окружности, равную длине дуги. Весь круг равен 360 °. Допустим, наша часть составляет 72 °. Мы делаем дробь, помещая часть поверх целого, и получаем \ (\ frac {72} {360} \), который сокращается до \ (\ frac {1} {5} \).Таким образом, длина нашей дуги будет составлять одну пятую от общей длины окружности. Теперь нам просто нужно найти эту окружность.
Окружность может быть найдена по формуле C = πd, когда мы знаем диаметр, и C = 2πr, когда мы знаем радиус, как мы это делаем здесь. Подставляя радиус 3 в формулу, мы получаем C = 6π метра или приблизительно 18,8495559 м.
Теперь мы умножаем это на \ (\ frac {1} {5} \) (или его десятичный эквивалент 0,2), чтобы найти длину нашей дуги, которая составляет 3,769911 метра. Обратите внимание, что нашими единицами измерения всегда будет длина.
Как найти площадь сектораТак же, как длина каждой дуги составляет часть окружности всего круга, площадь сектора — это просто часть площади круга. Итак, чтобы найти площадь сектора, нам нужно найти часть круга, образованного центральным углом, который мы знаем, а затем найти площадь всего круга, образованного известным нам радиусом. Затем мы просто умножаем их вместе. Давайте попробуем пример, где центральный угол равен 72 °, а радиус — 3 метра.
Во-первых, давайте найдем долю площади круга, которую занимает наш сектор. Весь круг равен 360 °. Наша часть 72 °. Мы делаем дробь, помещая часть поверх целого, и получаем \ (\ frac {72} {360} \), который сокращается до \ (\ frac {1} {5} \). Таким образом, площадь нашего сектора будет составлять одну пятую от общей площади круга. Теперь нам просто нужно найти эту область.
Площадь определяется по формуле A = πr2. Подставляя радиус 3 в формулу, мы получаем A = 9π квадратных метров или приблизительно 28.27433388 м2.
Теперь мы умножаем это на \ (\ frac {1} {5} \) (или его десятичный эквивалент 0,2), чтобы найти площадь нашего сектора, которая составляет 5,654867 квадратных метров. Обратите внимание, что нашим ответом всегда будет площадь, поэтому единицы всегда будут возведены в квадрат.
Радиус дуги или дуги с калькулятором
Радиус дуги или дуги с калькулятором — Math Open Reference Определение: радиус дуга или же сегмент это радиус круга, частью которого он является.Формула и калькулятор приведены ниже для радиуса с учетом ширины и высоты дуги.
Попробуйте это Перетащите одну из оранжевых точек, чтобы изменить высоту или ширину дуги. Показана расчетная площадь.
Дуги окружности
часто появляются в реальном мире, например в верхней части окна, показанного справа.
При их построении мы часто знаем ширину и высоту дуги, а также радиус.
Это позволяет нам провести дугу с помощью большого циркуля.
Для расчета радиуса
Учитывая дугу или сегмент с известной шириной и высотой: Формула для радиуса: где:
W — длина хорды, определяющей основание дуги.
H — высота, измеренная в средней точке основания дуги.
Вывод
См. Раздел «Как выводится формула радиуса дуги».
Калькулятор
Введите любые два значения и нажмите «Рассчитать». Недостающее значение будет вычислено.Например, введите ширину и высоту, затем нажмите «Рассчитать», чтобы получить радиус. Он работает для дуг длиной до полукруга, поэтому вводимая высота должна быть меньше половины ширины.
Определение ширины и высоты дуги
Ширина, высота и радиус дуги взаимосвязаны. Если вы знаете любых двух из них, вы можете найти третий. Подробнее об этом см. Стрелец (высота) дуги
Использование циркуля и линейки
Круг, проходящий через любые три точки, также можно найти, построив с помощью циркуля и линейки.Это также дает местоположение центральной точки и, следовательно, ее радиус. В апплете вверху страницы можно использовать три оранжевые точки. Видеть Построение круга через три точки.Другие темы в круге
Общие
Уравнения окружности
Углы по окружности
Дуги
(C) Открытый справочник по математике, 2011 г.
Все права защищены.
Калькулятор длины дуги
Что такое калькулятор длины дуги?
Часть кривой или часть окружности называется дугой.Длина дуги определяется как промежуток между двумя точками на участке кривой.
Калькулятор длины дугиCuemath — это онлайн-инструмент, который рассчитывает длину дуги за несколько секунд.
Как пользоваться калькулятором длины дуги?
Для использования калькулятора длины дуги выполните шаги, указанные ниже.
- Шаг 1: Введите значение радиуса и угла, образованного сектором в центре окружности.
- Шаг 2: Нажмите « Рассчитать », чтобы найти длину дуги.
- Шаг 3: Нажмите « Сброс », чтобы сбросить поля и ввести новые значения.
Как рассчитать длину дуги?
Когда θ выражается в радианах, длина дуги равна θ, умноженному на радиус окружности.
Длина дуги (L) = θ × r
Когда θ в градусах, формула длины дуги имеет вид,
Длина дуги (L) = θ × (п / 180) × r
Решенный пример 1:Найдите длину дуги, отрезанной центральным углом в 4 радиана в окружности с радиусом 6 единиц.
Решение:Поскольку угол выражается в радианах, воспользуемся следующей формулой.
Длина дуги (L) = θ × r
Подставляя значения радиуса и угла ( θ ) в формулу длины дуги:
Длина дуги = θ × r
= (4 × 6) единиц
= 24 единицы
Следовательно, длина дуги составляет 24 единицы
Решенный пример 2:Найдите длину дуги, отсеченной на центральный угол 25 градусов в окружности с радиусом 5 единиц.
Решение:Поскольку угол указывается в градусах, мы будем использовать следующую формулу
Длина дуги (L) = θ × (п / 180) × r
Подставьте значения радиуса и угла ( θ ) в формулу длины дуги:
Длина дуги = θ × (п / 180) × r
= 25 × (3,14 / 180) × 5
= 2,18 единиц.
Следовательно, длина дуги равна 2.18 шт.
Теперь воспользуйтесь калькулятором и найдите длину дуги, радиус и угол которой следующие.
- Радиус = 20 единиц, Угол = 2 радиана
- Радиус = 189 единиц, Угол = 128 °
Статьи по теме
длина дуги = [радиус • центральный угол (радианы)] длина дуги = окружность • [центральный угол (градусы) ÷ 360] Зная две из этих трех переменных, вы можете вычислить третью. Еще проще , этот калькулятор может решить эту проблему за вас. Вы хотите решить для ИНСТРУКЦИИ Начните с нажатия «Длина дуги», «Радиус» или «Центральный угол». 2) Круг имеет длину дуги 5,9 и центральный угол 1,67 радиана. Какой радиус? 3) Угол имеет длину дуги 2 и радиус 2. Что такое центральный угол? Числа отображаются в экспоненциальном представлении с указанием количества
значащие цифры, которые вы указываете. Для удобства чтения числа от 0,001 до 1000.
будет не в экспоненциальной нотации, но все равно будет иметь ту же точность. |
Дуга окружности, онлайн-калькулятор и формула
Онлайн калькуляторы и формулы для расчета дуги окружности
Расчет дуги окружности
Эта функция вычисляет длину дуги или угол ограничивающих ее прямых. Радиус и угол или длина дуги должны быть указаны в качестве аргументов.
Формула для расчета дуги окружности
Дуга — это часть контура круга. Он определяется двумя прямыми линиями, начинающимися из центральной точки, которые пересекают круговую линию под определенным углом α.
Поскольку окружность окружности составляет 360 градусов, длину дуги l можно рассчитать по следующей формуле:
\ (\ Displaystyle л = \ гидроразрыва {2 · г · π · α} {360} \) \ (\ Displaystyle α = \ гидроразрыва {360 · l} {2 · г · π} \)
Другие функции точек и линий
|
.



 Входное и выходное сопротивления равны 50 Ом. Описание: первый каскад работает в классе …
Входное и выходное сопротивления равны 50 Ом. Описание: первый каскад работает в классе …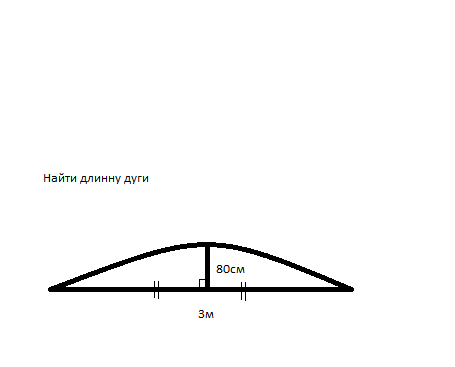
 Варианты исходных данных: длина дуги и диаметр, длина дуги и хорда; найти высоту сегмента.
Варианты исходных данных: длина дуги и диаметр, длина дуги и хорда; найти высоту сегмента. com/class-a-amplifier-by-transistor/
com/class-a-amplifier-by-transistor/ Преобразователь напряжения весьма прост, он состоит из микросхемы TL496 и конденсатора и дросселя на 50мкГн. Выходной ток преобразователя может достигать 400мА (не гарантировано выходное напряжение 9В). Ток потребления преобразователя без нагрузки 125мкА.
Преобразователь напряжения весьма прост, он состоит из микросхемы TL496 и конденсатора и дросселя на 50мкГн. Выходной ток преобразователя может достигать 400мА (не гарантировано выходное напряжение 9В). Ток потребления преобразователя без нагрузки 125мкА.