Площадь четырехугольника
Площадь произвольного четырехугольника, формулы и калькулятор для вычисления в режиме онлайн.
Площадь четырехугольника — это численная характеристика, характеризующая размер плоскости, ограниченной геометрической фигурой, образованной четырьмя последовательно соединенными отрезками.
Для вычисления площади произвольного четырехугольника применяются различные формулы, в зависимости от известных исходных данных. Ниже приведены формулы и калькулятор, который поможет вычислить площадь произвольного четырехугольника или проверить уже выполненные вычисления.
В окончании статьи приведены ссылки для вычисления частных случаев четырехугольников: квадрата, трапеции, параллелограмма, прямоугольника, ромба.
1
Площадь четырехугольника по диагоналям и углу между ними
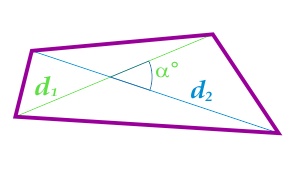
d1
d2 — диагональ
α° — угол между диагоналями
… подготовка …
2
Площадь четырехугольника через стороны и углы между этими сторонами
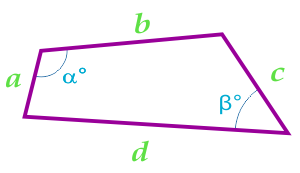
При вычислении площади четырехугольника с использованием данной формулы, необходимо предварительно вычислить полупериметр четырехугольника по формуле:
a — сторона
b — сторона
d — сторона
α° — угол между сторонами
β° — угол между сторонами
… подготовка …
3
Площадь четырехугольника вписанного в окружность, вычисляемая по Формуле Брахмагупты
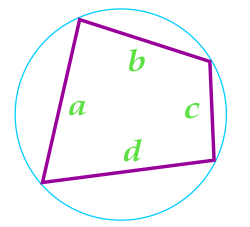
Данная формула справедлива только для четырехугольников, вокруг которых можно описать окружность.
При вычислении площади четырехугольника с использованием данной формулы, необходимо предварительно вычислить полупериметр четырехугольника по формуле:
a — сторона
b — сторона
c — сторона
d — сторона
… подготовка …
4
Площадь четырехугольника в который можно вписать окружность
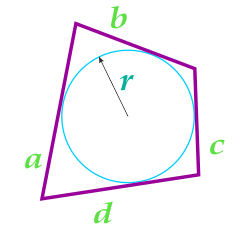
Данная формула справедлива только для четырехугольников, в которые можно вписать окружность. Вписанная окружность должна иметь точки соприкосновения со всеми четырьмя сторонами четырехугольника.
При вычислении площади четырехугольника с использованием данной формулы, необходимо предварительно вычислить полупериметр четырехугольника по формуле:
a — сторона
b — сторона
c — сторона
d — сторона
r — радиус вписанной окружности
… подготовка …
5
Площадь четырехугольника в который можно вписать окружность, определяемая через стороны и углы между ними
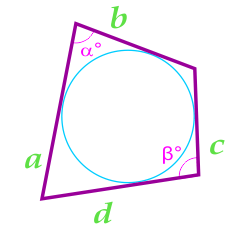
Данная формула справедлива только для четырехугольников, в которые можно вписать окружность. Вписанная окружность должна иметь точки соприкосновения со всеми четырьмя сторонами четырехугольника.
a — сторона
b — сторона
c — сторона
d — сторона
α° — угол между сторонами
… подготовка …
Определения
Четырехугольник – это геометрическая плоская фигура, образованная четырьмя последовательно соединенными отрезками.
Площадь – это численная характеристика, характеризующая размер плоскости, ограниченной замкнутой геометрической фигурой.
Площадь измеряется в единицах измерения в квадрате: км2, м2, см2, мм2 и т.д.
Если в исходных данных угол задан в радианах, то для перевода в градусы вы можете воспользоваться нашим «Конвертером величин». Или вычислить самостоятельно по формуле: 1 рад × (180/π) ° = 57,296°
Для вычисления частных случаев четырехугольников можно воспользоваться формулами и калькуляторами, приведенными в других статьях сайта:
doza.pro
Подготовка школьников к ЕГЭ и ОГЭ (Справочник по математике — Планиметрия
В данном разделе рассматриваются только выпуклые фигуры, и считается известной формула:
S = ab,
которая позволяет найти площадь прямоугольникапрямоугольника с основанием a и высотой b.
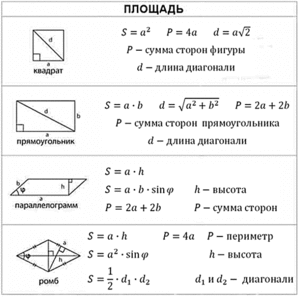
Формулы для площадей четырехугольников
| Четырехугольник | Рисунок | Формула площади | Обозначения |
| Прямоугольник | 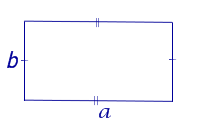 | S = ab | a и b – смежные стороны |
 |
Посмотреть вывод формулы | d – диагональ, | |
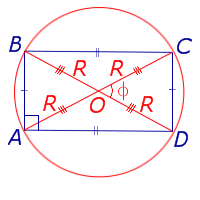 | S = 2R2 sin φ Получается из верхней формулы подстановкой d=2R | R – радиус описанной окружности, | |
| Параллелограмм | 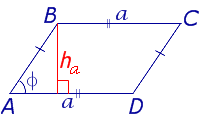 | S = a ha Посмотреть вывод формулы | a – сторона, |
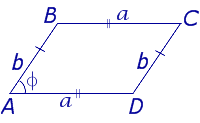 | S = absin φ Посмотреть вывод формулы | a и b – смежные стороны, | |
 |
Посмотреть вывод формулы | d1, d2 – диагонали, φ – любой из четырёх углов между ними | |
| Квадрат | 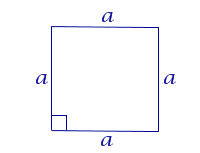 | S = a2 | a – сторона квадрата |
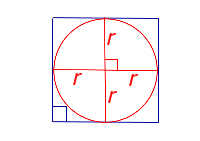 | S = 4r2 | r – радиус вписанной окружности | |
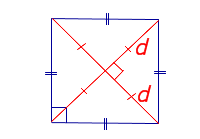 |
Посмотреть вывод формулы | d – диагональ квадрата | |
 | S = 2R2 Получается из верхней формулы подстановкой d = 2R | R – радиус описанной окружности | |
| Ромб | 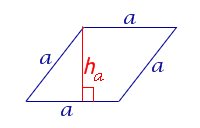 | S = a ha Посмотреть вывод формулы | a – сторона, |
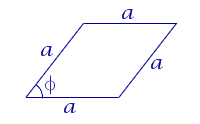 | S = a2 sin φ Посмотреть вывод формулы | a – сторона, | |
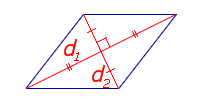 |
Посмотреть вывод формулы | d1, d2 – диагонали | |
 | S = 2ar Посмотреть вывод формулы | a – сторона, | |
 |
Посмотреть вывод формулы | r – радиус вписанной окружности, | |
| Трапеция | 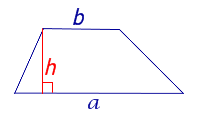 |
Посмотреть вывод формулы | a и b – основания, |
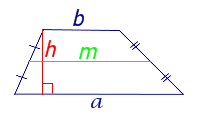 | S = m h | m – средняя линия, | |
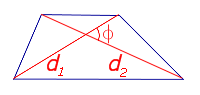 |
Посмотреть вывод формулы | d1, d2 – диагонали, φ – любой из четырёх углов между ними | |
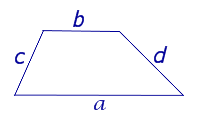 |
Посмотреть вывод формулы | a и b – основания, | |
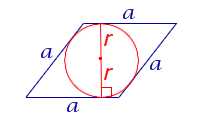
| Дельтоид | 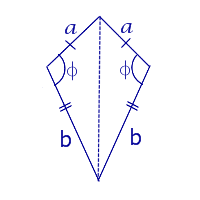 | S = ab sin φ | a и b – неравные стороны, |
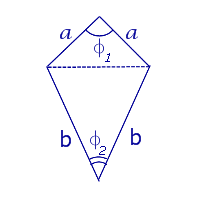 | 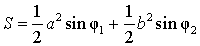 | a и b – неравные стороны, | |
 | S = (a + b) r Посмотреть вывод формулы | a и b – неравные стороны, | |
 |
Посмотреть вывод формулы | d1, d2 – диагонали | |
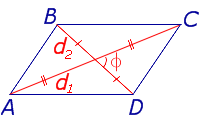
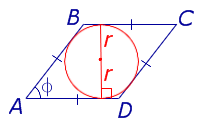
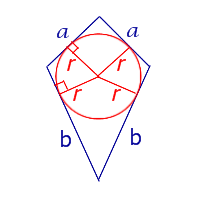
| Произвольный выпуклый четырёхугольник | 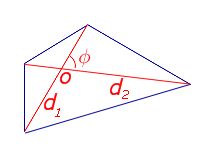 |
Посмотреть вывод формулы | d1, d2 – диагонали, φ – любой из четырёх углов между ними |
| Вписанный четырёхугольник | 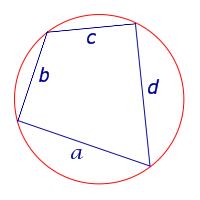 |
Посмотреть вывод формулы Брахмагупты | a, b, c, d – длины сторон четырёхугольника, Формулу называют «Формула Брахмагупты» |
| Прямоугольник | |
 | S = ab где |
 |
где Посмотреть вывод формулы |
 | S = 2R2 sin φ где Формула получается из верхней формулы подстановкой d = 2R |
| Параллелограмм | |
 | S = a ha где Посмотреть вывод формулы |
 | S = absin φ где Посмотреть вывод формулы |
 |
где φ – любой из четырёх углов между ними Посмотреть вывод формулы |
| Квадрат | |
 | S = a2 где |
 | S = 4r2 где |
 |
где Посмотреть вывод формулы |
 | S = 2R2 где Получается из верхней формулы подстановкой d = 2R |
| Ромб | |
 | S = a ha где Посмотреть вывод формулы |
 | S = a2 sin φ где Посмотреть вывод формулы |
 |
где Посмотреть вывод формулы |
 | S = 2ar где Посмотреть вывод формулы |
 |
где Посмотреть вывод формулы |
| Трапеция | |
 |
где Посмотреть вывод формулы |
 | S = m h где |
 |
где φ – любой из четырёх углов между ними Посмотреть вывод формулы |
 |
где Посмотреть вывод формулы |
| Дельтоид | |
 | S = ab sin φ где |
 | 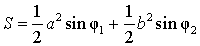 где |
 | S = (a + b) r где Посмотреть вывод формулы |
 |
где Посмотреть вывод формулы |
| Произвольный выпуклый четырёхугольник | |
 |
где φ – любой из четырёх углов между ними Посмотреть вывод формулы |
| Вписанный четырёхугольник | |
 |
где Формулу называют «Формула Брахмагупты» Посмотреть вывод формулы Брахмагупты |
| Прямоугольник |
 S = ab где |

где Посмотреть вывод формулы |
 S = 2R2 sin φ где Формула получается из верхней формулы подстановкой d = 2R |
| Параллелограмм |
 S = a ha где Посмотреть вывод формулы |
 S = absin φ где Посмотреть вывод формулы |

где φ – любой из четырёх углов между ними Посмотреть вывод формулы |
| Квадрат |
 S = a2 где |
 S = 4r2 где |

где Посмотреть вывод формулы |
 S = 2R2 где Получается из верхней формулы подстановкой d = 2R |
| Ромб |
 S = a ha где Посмотреть вывод формулы |
 S = a2 sin φ где Посмотреть вывод формулы |

где Посмотреть вывод формулы |
 S = 2ar где Посмотреть вывод формулы |

где Посмотреть вывод формулы |
| Трапеция |

где Посмотреть вывод формулы |
 S = m h где |

где φ – любой из четырёх углов между ними Посмотреть вывод формулы |
 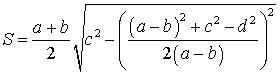 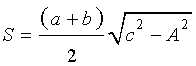 где Посмотреть вывод формулы |
| Дельтоид |
 S = ab sin φ где |

где |
 S = (a + b) r где Посмотреть вывод формулы |

где Посмотреть вывод формулы |
| Произвольный выпуклый четырёхугольник |

где φ – любой из четырёх углов между ними Посмотреть вывод формулы |
| Вписанный четырёхугольник |
 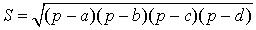 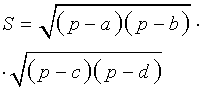 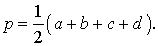 где Формулу называют «Формула Брахмагупты» Посмотреть вывод формулы Брахмагупты |
Вывод формул для площадей четырехугольников
Утверждение 1. Площадь выпуклого четырёхугольника можно найти по формуле
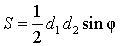
где d1 и d2 – диагонали четырёхугольника, а φ – любой из четырёх углов между ними (рис. 1).
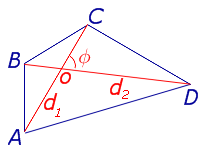
Рис. 1
Доказательство. В соответствии с рисунком 1 справедливо равенство:
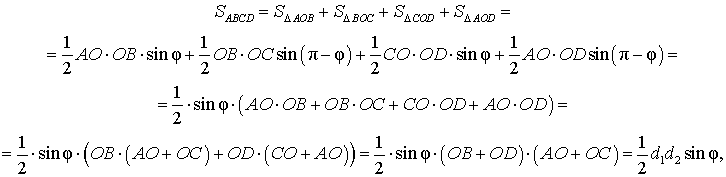
что и требовалось доказать.
Утверждение 2. Площадь параллелограммапараллелограмма можно найти по формуле
S = a ha ,
где a – сторона параллелограмма, а ha – высотавысотавысота, опущенная на эту сторону (рис. 2).
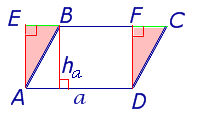
Рис. 2
Доказательство. Поскольку прямоугольный треугольник DFC равен прямоугольному треугольнику AEB (рис.26), то четырёхугольник AEFB – прямоугольник. Поэтому
SABCD = SAEFD = a ha ,
что и требовалось доказать.
Утверждение 3.Площадь параллелограмма параллелограмма можно найти по формуле
S = ab sin φ,
где a и b – смежные стороны параллелограмма, а φ – угол между ними (рис. 3).
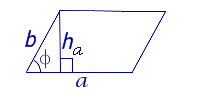
Рис. 3
Доказательство. Поскольку
ha = b sin φ,
то, в силу утверждения 2, справедлива формула
S = a ha = ab sin φ,
что и требовалось доказать.
Утверждение 4. Площадь ромбаромба можно найти по формуле
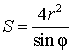 ,
,
где r – радиус вписанной в ромб окружности, а φ – любой из четырёх углов ромба (рис.4).
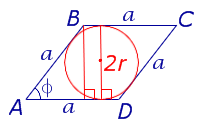
Рис. 4
Доказательство. Поскольку каждая из диагоналей ромба является биссектрисой угла, а каждая точка биссектрисы угла равноудалена от сторон угла, то точка пересечения диагоналей ромба равноудалена от всех сторон ромба и является центром вписанной в ромб окружности. Отсюда следует, в частности, что высота ромба в 2 раза больше радиуса вписанной окружности (рис.4). Поэтому
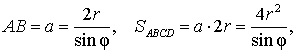
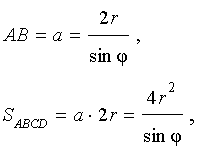
что и требовалось доказать.
Утверждение 5. Площадь трапеции можно найти по формуле
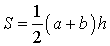 ,
,
где a и b – основания трапеции, а h – высотавысотавысота (рис.5).
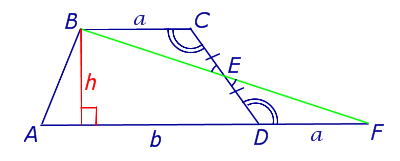
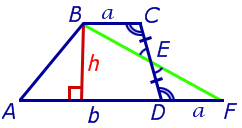
Рис. 5
Доказательство. Проведём прямую BE через вершину B трапеции и середину E боковой стороны CD. Точку пересечения прямых AD и BE обозначим буквой F (рис. 5). Поскольку треугольник BCE равен треугольнику EDF (по стороне и прилежащим к ней углам), то площадь трапеции ABCD равна площади треугольника ABF. Поэтому
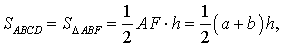
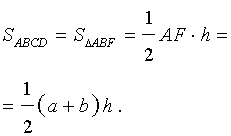
что и требовалось доказать.
Утверждение 6. Площадь трапеции трапеции можно найти по формуле
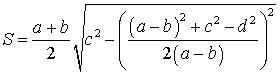 ,
,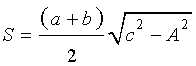
где a и b – основания, а c и d – боковые стороны трапеции,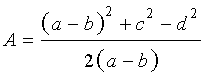
(рис.6).
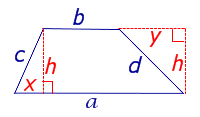
Рис. 6
Доказательство. Воспользовавшись теоремой Пифагора, составим следующую систему уравнений с неизвестными x, y, h (рис. 6):
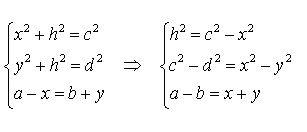
Следовательно,
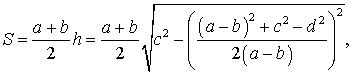
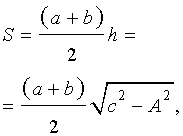
где
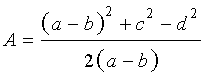 ,
,что и требовалось доказать.
Утверждение 7. Площадь дельтоида, дельтоида, можно найти по формуле:
S = (a + b) r,
где a и b – неравные стороны дельтоида, а r – радиус вписанной в дельтоид окружности (рис.7).
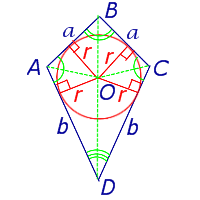
Рис. 7
Доказательство. Докажем сначала, что в каждый дельтоид можно вписать окружность. Для этого заметим, что треугольники ABD и BCD равны в силу признака равенства треугольников «По трём сторонам» (рис. 7). Отсюда вытекает, что диагональ BD является биссектрисой углов B и D, а биссектрисы углов A и C пересекаются в некоторой точке O, лежащей на диагонали BD. Точка O и является центром вписанной в дельтоид окружности.
Если r – радиус вписанной в дельтоид окружности, то
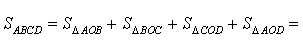
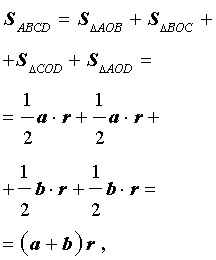
что и требовалось доказать.

На нашем сайте можно также ознакомиться нашими учебными материалами для подготовки к ЕГЭ и ОГЭ по математике.
www.resolventa.ru
Площадь четырехугольника — формулы, примеры расчета
Четырехугольником называется фигура, состоящая из четырех вершин, три из которых не лежат на одной прямой, и отрезков, соединяющих их.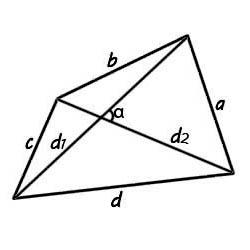
Существует множество четырехугольников. К ним относятся параллелограммы, квадраты, ромбы, трапеции. Найти площадь квадрата можно найти по сторонам, площадь ромба легко вычисляется по диагоналям. В произвольном четырехугольнике также можно использовать все элементы для вывода формулы площади четырехугольника. Для начала рассмотрим формулу площади четырехугольника через диагональ. Для того, чтобы ее использовать потребуются длины диагоналей и размер острого угла между ними. Зная необходимые данные можно проводить пример расчета площади четырехугольника по такой формуле:
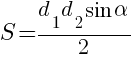
Половина произведения диагоналей и синуса острого угла между ними является площадью четырехугольника. Рассмотрим пример расчета площади четырехугольника через диагональ.
 Пусть дан четырехугольник с двумя диагоналями d1=5 см;d2=4см. Острый угол между ними равен α = 30°. Формула площади четырехугольника через диагонали легко применяется для известных условий. Подставим данные:
Пусть дан четырехугольник с двумя диагоналями d1=5 см;d2=4см. Острый угол между ними равен α = 30°. Формула площади четырехугольника через диагонали легко применяется для известных условий. Подставим данные: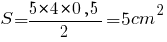
На примере расчета площади четырехугольника через диагонали понимаем, что формула очень похожа на расчет площади параллелограмма.
Площадь четырехугольника по сторонам
Когда известны длины сторон фигуры, можно применить формулу площади четырехугольника по сторонам. Для применения этих расчетов потребуется найти полупериметр фигуры. Мы помним, что периметр – это сумма длин всех сторон. Полупериметр – это половина периметра. В нашем прямоугольнике со сторонами a, b, c, d формула полупериметра будет выглядеть так: 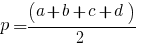
Зная стороны, выводим формулу. Площадь четырехугольника представляет собой корень из произведения разности полупериметра с длиной каждой стороны:

 Рассмотрим пример расчета площади четырехугольника через стороны. Дан произвольный четырехугольник со сторонами a = 5 см, b = 4 см, с = 3 см, d = 6 см. Для начала найдем полупериметр:
Рассмотрим пример расчета площади четырехугольника через стороны. Дан произвольный четырехугольник со сторонами a = 5 см, b = 4 см, с = 3 см, d = 6 см. Для начала найдем полупериметр: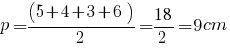
используем найденное значение для расчета площади:

Площадь четырехугольника, заданного координатами
Формула площади четырехугольника по координатам используется для расчета площади фигур, которые располагаются в системе координат. В этом случае для начала требуется расчет длин необходимых сторон. В зависимости от типа четырехугольника может меняться и сама формула. Рассмотрим пример расчета площади четырехугольника, используя квадрат, который лежит в системе координат XY.
2mb.ru
Онлайн калькулятор: Площадь четырехугольника
Есть несколько способов найти площадь неправильного четырехугольника.
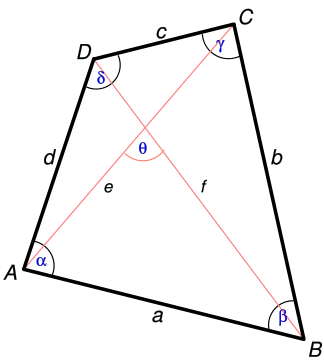 https://en.wikipedia.org/wiki/File:Tetragon_measures.svg
https://en.wikipedia.org/wiki/File:Tetragon_measures.svgКартинка: википедия
- Вы знаете длины диагоналей и размер угла между ними. Тогда площадь четырехугольника можно найти по формуле
Калькулятор:

Площадь выпуклого четырехугольника
Угол между диагоналямиТочность вычисленияЗнаков после запятой: 2
save Сохранить share Поделиться extension Виджет
- Вы знаете длины четырех сторон и размеры двух противолежащих углов. Тогда площадь четырехугольника можно найти по формуле Бретшнайдера.
,
где s — полупериметр.
Калькулятор:

Площадь четырехугольника по четырем сторонам и двум противолежащим углам
Точность вычисленияЗнаков после запятой: 2
save Сохранить share Поделиться extension Виджет
- Вы знаете длины четырех сторон и длины диагоналей. Тогда площадь четырехугольника тоже можно найти по формуле Бретшнайдера.
,
где s — полупериметр
Калькулятор:

Площадь четырехугольника по четырем сторонам и двум диагоналям
Точность вычисленияЗнаков после запятой: 2
planetcalc.ru
Формулы вычисления площади произвольного четырёхугольника
В школьных математических заданиях часто требуется определить площадь четырёхугольника. Все довольно просто, если задан частный случай фигуры — квадрат, ромб, прямоугольник, трапеция, параллелограмм, ромбоид. В случае же произвольного четырёхугольника все несколько сложнее, но также вполне доступно для среднего школьника. Ниже мы изучим различные методы расчётов площади произвольных четырёхугольников, запишем формулы и рассмотрим различные вспомогательные примеры.
Определения и соглашения
В приведённой ниже таблице будут указаны определения и договорённости, которые будут использоваться в дальнейшем во время наших рассуждений.
 Четырёхугольник — это фигура из четырёх точек (вершин), из которых любые три не лежат на одной прямой, и четырёх отрезков (сторон) последовательно их соединяющих.
Четырёхугольник — это фигура из четырёх точек (вершин), из которых любые три не лежат на одной прямой, и четырёх отрезков (сторон) последовательно их соединяющих.- Диагональ — отрезок, соединяющий вершины многоугольника не лежащие на одной стороне (её обозначение – латинская буква d).
- Площадь фигуры — это численное значение территории, заключённой внутри многоугольника (её обозначение – латинская буква S).
- Синус угла — это число равное отношению противоположного катета к гипотенузе в прямоугольном треугольнике. (её обозначение – запись sin).
- Косинус угла — это число равное отношению прилежащего катета к гипотенузе в прямоугольном треугольнике. В дальнейшем в статье для его обозначения будем использовать латинскую запись cos.
- Описанная окружность — это окружность, которой принадлежат все вершины многоугольника ( её радиуса обозается буквой R).
- Вписанная окружность — это окружность, которая касается всех сторон многоугольника. В дальнейшем в статье для обозначения её радиуса будем использовать латинскую букву r.
- Угол между сторонами a и b будем обозначать следующей записью (a,b).

Нахождение площади четырёхугольника различными способами и методами
Узнаем как найти площадь четырёхугольника когда даны его диагонали и образуемый при их пересечении острый угол. Тогда площадь четырёхугольника будет вычисляться по формуле: S = 1/2*d1*d2*sin(d1,d2).
Рассмотрим пример. Пусть d1 = 15 сантиметров, d2 = 12 сантиметров, и угол между ними 30 градусов. Определим S. S = 1/2*15*12*sin30 = 1/2*15*12*1/2 = 45 сантиметров квадратных.
Теперь пусть даны стороны и противолежащие углы четырёхугольника.
Пусть a, b, c, d известные стороны многоугольника; p — его полупериметр. Корень квадратный выражения условимся обозначать как rad (от латинского radical). Формула площади четырёхугольника будет находиться по формуле: S = rad(( p − a ) ( p − b ) ( p − c ) ( p − d ) − a b c d ⋅ c o s^2( (a,b) + (c,d))/2), где p = 1/2*(a + b + c + d).
На первый взгляд, формула кажется очень сложной и вычурной. Однако ничего сложного здесь нет, что мы и докажем, рассмотрев пример. Пусть данные нашего условия следующие: a = 18 миллиметров, b = 23 миллиметра, c = 22 миллиметра, d = 17 миллиметров. Противолежащие углы будут равны (a,b) = 0,5 градуса и (c,d) = 1,5 градуса. Для начала находим полупериметр: p = 1/2*(18 + 23 + 22 + 17) = 1/2*80 = 40 миллиметров.
Теперь найдём квадрат косинуса полусуммы противолежащих углов: c o s^2( (a,b) + (c,d))/2) = c o s^2(0,5 + 1,5)/2 = c o s1*c o s1 = (1/2)*(1/2) = 0,9996.
Подставим полученные данные в нашу формулу, получим: S = rad((40 — 18)*(40 — 23)*(40 — 22)*(40 — 17) — 18*23*22*17*0,97) = rad(22*17*18*23 — 18*23*22*17*1/4) = rad((22*17*18*23*(1 — 0,9996)) = rad(154836*0,0004) = rad62 = 7,875 миллиметра квадратного.
Разберёмся как находить площадь с помощью вписанной и описанной окружностей. При решении задач данной темы имеет смысл сопровождать свои действия вспомогательным рисунком, хотя это требование и не является обязательным.
Если есть вписанная окружность и нужно найти площадь четырёхугольника формула имеет вид:
S = ((a + b+ c + d)/2)*r
Снова возьмём на рассмотрение пример: a = 16 метров, b = 30 метров, c = 28 метров, d = 14 метров, r = 6 метров. Подставим аши значения в формулу, получим:
S = ((16 +30 + 28 + 14)/2)*6 = 44*6 = 264 метров квадратных.
Теперь займёмся вариантом когда окружность описана вокруг четырёхугольника. Здесь мы сможем воспользоваться следующей формулой:
S = rad((p − a )*( p − b )*( p − c )*( p − d ), где p равно половине длины периметра. Пускай в нашем случае стороны имеют следующие значения a = 26 дециметров, b = 35 дециметров, c = 39 дециметров, d = 30 дециметров.
Первым делом определим полупериметр, p = (26 + 35 + 39 + 30)/2 = 65 дециметров. Подставим найденное значение в нашу формулу. Получим:
S = rad((65 — 26)*(65 — 35)*(65 — 39)*(65 — 30)) = rad(39*30*26*35) = 1032 (округлённо) дециметров квадратных.
Заключение
Внимательно изучив все вышеизложенное, можно сделать вывод — определение площади произвольного четырёхугольника с разными сторонами сложнее, чем у них же специальных видов — квадрата, прямоугольника, ромба, трапеции, параллелограмма. Однако внимательно изучив все приведённые методы, можно с лёгкостью решать задачи необходимые для школьников. Сведём все наши формулы в одну таблицу:
- S = 1/2*d1*d2*sin(d1,d2);
- S = rad(( p − a )*( p − b )*( p − c )*( p − d ) − a*b*c*d*c o s^2( (a,b) + (c,d))/2), где p = 1/2*(a + b + c + d);
- S = ((a + b+ c + d)/2)*r
S = rad((p − a )*( p − b )*( p − c )*( p − d ), где p равно половине периметра.
Таким образом, реально сложной является только формула номер 2, но и она вполне доступна, при условии хорошего понимания данных в статье определений и соглашений.
Видео
Разобраться в этой теме вам поможет видео.
liveposts.ru
|
Четырёхугольником называется фигура, которая состоит из четырёх точек (вершин) и четырёх отрезков (сторон), которые последовательно соединяют вершины. При этом никакие три из данных точек не должны лежать на одной прямой, а соединяющие их отрезки не должны пересекаться. Четырёхугольник называется выпуклым, если он расположен в одной полуплоскости относительно прямой, которая содержит любую из его сторон. Сумма углов выпуклого четырёхугольника равна 360°: ∠A+∠B+∠C+∠D=360°. Не существует четырёхугольников, у которых все углы острые или все углы тупые. Каждый угол четырёхугольника всегда меньше суммы трёх остальных углов: ∠A < ∠B+∠C+∠D, ∠B < ∠A+∠C+∠D, ∠C < ∠A+∠B+∠D, ∠D < ∠A+∠B+∠D. Каждая сторона четырёхугольника всегда меньше суммы трёх остальных сторон: a < b+c+d, b < a+c+d, c < a+b+d, d < a+b+c. Площадь произвольного выпуклого четырёхугольника равна: |
||
|
Диагоналями четырёхугольника называются отрезки, соединяющие его противолежащие вершины. Диагонали выпуклого четырёхугольника пересекаются, а невыпуклого – нет. Площадь произвольного выпуклого четырёхугольника: |
||
|
Если M, N, P, Q – середины сторон выпуклого четырёхугольника ABCD, а R, S – середины его диагоналей, то четырёхугольники MNPQ, MRPS, NSQR являются параллелограммами и называются параллелограммами Вариньона. Форма и размеры параллелограммов Вариньона связаны с формой и размерами данного четырёхугольника ABCD. Так MNPQ – прямоугольник, если диагонали четырёхугольника ABCD перпендикулярны; MNPQ – ромб, если диагонали четырёхугольника ABCD равны; MNPQ – квадрат, если диагонали четырёхугольника ABCD перпендикулярны и равны; SABCD = 2SMNPQ . |
||
|
Отрезки MP, NQ и RS называются первой, второй и третьей средними линиями выпуклого четырёхугольника. В параллелограмме, и только в нём, середины диагоналей совпадают, и потому третья средняя линия вырождается в точку. Для других четырёхугольников средние линии – отрезки. Все средние линии четырёхугольника пересекаются в одной точке и делятся ею пополам: MG=GP, NG=GQ, RG=GS . Сумма квадратов средних линий четырёхугольника равна четверти суммы квадратов всех его сторон и диагоналей: MP2+ NQ2+ RS 2 = ¼(AB2+BC2+CD2+AD2+AC2+BD2). Если β – угол между первой и второй средними линиями четырёхугольника, то его площадь: SABCD = MP·NQ·sinβ. |
||
|
|
||
|
Равными плитками, которые имеют форму произвольного, не обязательно выпуклого, четырёхугольника можно замостить плоскость так, чтобы не было наложений плиток друг на друга и не осталось непокрытых участков плоскости. |
||
|
Четырёхугольник называется описанным около окружности (описанным), если существует такая окружность, которая касается всех его сторон, тогда сама окружность называется вписанной. Четырёхугольник является описанным тогда и только тогда, кода суммы его противолежащих сторон равны: a+c = b+d. Для сторон описанного четырёхугольника и радиуса вписанной в него окружности верно: a+c ≥ 4r, b+d ≥ 4r. Площадь описанного четырёхугольника: S = pr, где r – радиус вписанной окружности, p – полупериметр четырёхугольника. Площадь описанного четырёхугольника: |
||
|
Центр вписанной в четырёхугольник окружности является точкой пересечения биссектрис всех четырёх углов этого четырёхугольника. Точки касания вписанной окружности отсекают равные отрезки от углов четырёхугольника: AK=AN, BK=BL, CL=CM, DM=DN. Если O – центр окружности, вписанной в четырёхугольник ABCD, то ∠AOB+∠COD=∠BOC+∠AOD=180°. Для описанного четырёхугольника ABCD со сторонами AB=a, BC=b, CD=c и AD=d верны соотношения: |
||
|
Четырёхугольник называется вписанным в окружность (вписанным), если существует окружность, проходящая через все его вершины, тогда сама окружность называется описанной около четырёхугольника. Выпуклый четырёхугольник является описанным тогда и только тогда, когда сумма его противолежащих углов равна 180°: ∠A+∠C=∠B+∠D=180°. Центр описанной около четырёхугольника окружности является точкой пересечения всех четырёх серединных перпендикуляров сторон этого четырёхугольника. |
||
|
Первая теорема Птолемея. Выпуклый четырёхугольник тогда и только тогда является вписанным, когда выполняется равенство: Вторая теорема Птолемея. Выпуклый четырёхугольник тогда и только тогда является вписанным, когда выполняется равенство: Радиус окружности, описанной около четырёхугольника: Площадь вписанного четырёхугольника: |
||
|
Диагонали выпуклого четырёхугольника разбивают каждый его угол на два угла. Углы, опирающиеся на одну сторону, называются связанными углами. Выпуклый четырёхугольник является вписанным тогда и только тогда, когда у него есть хотя бы одна пара равных связанных углов. У вписанного четырёхугольника любые два связанных угла равны. |
||
|
Если четырёхугольник одновременно является описанным и вписанным, то его площадь: Для радиусов описанной и вписанной окружностей данного четырёхугольника и расстояния между центрами этих окружностей выполняется соотношение: |
||
|
Параллелограммом называется четырёхугольник, противолежащие стороны которого попарно параллельны: AB||CD, BC||AD. У параллелограмма противолежащие стороны равны и противолежащие углы равны: AB=CD, BC=AD; ∠A=∠C, ∠B=∠D. Сумма любых двух соседних углов параллелограмма равна 180°: ∠A+∠B=∠B+∠C=∠C+∠D=∠A+∠D=180°. |
||
|
Диагонали параллелограмма пересекаются и точкой пересечения делятся пополам: AO=OC; BO=OD. Каждая диагональ делит параллелограмм на два равных треугольника: ∠ABC=∠CDA; ∠ABD=∠CDB. Две диагонали параллелограмма делят его на четыре равновеликих треугольника: SΔABO=SΔBCO=SΔCDO=SΔADO. Сумма квадратов диагоналей параллелограмма равна сумме квадратов всех его сторон: e2+f2 = a2+b2+a2+b2 = 2(a2+b2). |
||
|
Признаки параллелограмма:
|
||
|
Высотой параллелограмма называется перпендикуляр, проведённый из вершины параллелограмма к неприлежащей стороне: ha = b·sin γ; hb = a·sin γ. Площадь параллелограмма можно определить:
S = aha = bhb;
S = ab·sin γ. |
||
|
Ромбом называется параллелограмм, у которого все стороны равны: AB=BC=CD=AD. Диагонали ромба пересекаются под прямым углом и являются биссектрисами его углов: AC⊥BD; ∠ABD=∠CBD=∠ADB=∠CDB; ∠BAC=∠DAC=∠BCA=∠DCA. |
||
|
В любой ромб можно вписать окружность с центром в точке пересечения его диагоналей. Радиус окружности, вписанной в ромб, можно вычислить:
Площадь ромба можно определить:
|
||
|
Прямоугольником называется параллелограмм, у которого все углы прямые: ∠A=∠B=∠C=∠D=90°. |
||
|
Диагонали прямоугольника равны и точкой пересечения делятся на четыре равных отрезка: AC=BD; AO=BO=CO=DO. Площадь прямоугольника можно определить:
S = ab;
S = ½d²·sin γ. |
||
|
Около любого прямоугольника можно описать окружность с центром в точке пересечения его диагоналей и радиусом, который равен половине диагонали: BD = 2R. |
||
|
Квадрат – это прямоугольник, у которого все стороны равны: ∠A=∠B=∠C=∠D=90°, |
||
|
Диагонали квадрата равны и перпендикулярны. Сторона и диагональ квадрата связаны соотношениями: Площадь квадрата: |
||
|
У квадрата центры вписанной и описанной окружностей совпадают и находятся в точке пересечения его диагоналей. Радиус описанной окружности: Радиус вписанной окружности: |
||
|
Трапецией называется четырёхугольник у которого только две противолежащие стороны параллельны: AD||BC. Параллельные стороны называются основаниями трапеции, непараллельные – боковыми сторонами. Высота трапеции – перпендикуляр, проведённый из произвольной точки одного основания трапеции к прямой, содержащей другое основание трапеции. |
||
|
Средней линией (первой средней линией) трапеции называется отрезок, который соединяет середины боковых сторон данной трапеции: AK=KB; CL=LD. Средняя линия трапеции параллельна её основаниям и равна их полусумме: KL||AD; KL||BC; KL = ½(AD+BC). |
||
|
При продолжении до пересечения боковых сторон трапеции образуются два подобных треугольника с коэффициентом подобия, равным отношению основ: ΔAED∼ΔBEC, k=AD/BC. Треугольники, образованные основами и отрезками диагоналей подобны с коэффициентом подобия, равным отношению основ: ΔAОD∼ΔCОВ, k=AD/BC. Площади треугольников, образованных боковыми сторонами и отрезками диагоналей трапеции, равны: SΔABO = SΔCDO. |
||
|
Отрезок, соединяющий середины оснований (вторая средняя линия) трапеции, проходит через точку пересечения диагоналей, а его продолжение – через точку пересечения продолжений боковых сторон: O∈KL; E∈KL. Отрезок, соединяющий середины диагоналей (третья средняя линия) трапеции, параллелен основаниям и равен их полуразности: RS||AD; RS||BC; RS = ½(AD–BC). |
||
|
В трапецию можно вписать окружность, если сумма её основ равна сумме боковых сторон: AD+BC=AB+CD. Центром вписанной в трапецию окружности является точка пересечения биссектрис внутренних углов трапеции. В трапецию АВСD с основаниями AD и BC можно вписать окружность тогда и только тогда, когда выполняется хотя бы одно из равенств: Боковые стороны трапеции видны из центра окружности, вписанной в данную трапецию, под прямым углом: ∠AOB=∠COD=90°. Радиус вписанной в трапецию окружности можно определить:
|
||
|
Равнобокой называется трапеция, у которой боковые стороны равны: AB=CD. У равнобокой трапеции:
AC=BD;
∠A=∠D, ∠B=∠C;
∠A+∠C=∠B+∠D=180°. Около трапеции можно описать окружность тогда и только тогда, когда она равнобокая. Стороны и диагональ равнобокой трапеции связаны соотношением: d² = ab+c². |
||
|
Трапеция называется прямоугольной, если одна из её боковых сторон перпендикулярна основаниям. |
||
|
Площадь трапеции можно определить:
|
||
|
Дельтоид называется четырёхугольник, который имеет две пары равных соседних сторон. Дельтоид может быть выпуклым или невыпуклым. Прямые, содержащие диагонали любого дельтоида пересекаются под прямым углом. В любом дельтоиде углы между соседними неравными сторонами равны. Площадь любого дельтоида можно определить:
S = ab·sin α . |
||
|
В любой выпуклый дельтоид можно вписать окружность. Если выпуклый дельтоид не является ромбом, то существует окружность, касающаяся продолжений всех четырёх сторон данного дельтоида. Для невыпуклого дельтоида можно построить окружность, касающуюся двух сторон большей длины и продолжений двух меньших сторон, а также окружность, касающуюся двух меньших сторон и продолжений двух сторон большей длины. |
||
|
Вокруг дельтоида можно описать окружность тогда и только тогда, когда его неравные стороны образуют углы по 90°. Радиус окружности, описанной около дельтоида можно определить через две его неравные стороны:
|
||
|
Четырёхугольник называется ортодиагональным, если его диагонали пересекаются под прямым углом. Четырёхугольник является ортодиагональным тогда и только тогда, когда выполняется одно из условий:
|
||
|
Сумма квадратов противолежащих сторон вписанного в окружность ортодиагонального четырёхугольника равна квадрату диаметра описанной окружности: a²+c² = b²+d² = 4R². |
||
|
Ортодиагональный четырёхугольник является описанным около окружности тогда и только тогда, когда произведения его противолежащих сторон равны: ac = bd. Если ABCD – ортодиагональный четырёхугольник, описанный около окружности с центром в точке О, то верны соотношения: |
||
math4school.ru
Считаем площадь неправильного 4-х угольника
Следующий калькулятор был создан по неоднократному запросу создать калькулятор, который бы смог считать площадь неправильного четырехугольника, в котором известны длины сторон.
Все мы понимаем, что данный четырехугольник может иметь любой вид (параллелограмма, квадрата, прямоугольника и так далее). Углы могут быть совершенно разные. По этому был создан уникальный калькулятор, который в реальном режиме прорисовывает четырехугольник и сразу считает его площадь, длины сторон нужно задать сразу вверху калькулятора, а потом нажать остановить на том четырехугольнике, площадь которого вы хотите посчитать.
The field is not filled.
‘%1’ is not a valid e-mail address.
Please fill in this field.
The field must contain at least% 1 characters.
The value must not be longer than% 1 characters.
Field value does not coincide with the field ‘%1’
An invalid character. Valid characters:’%1′.
Expected number.
It is expected a positive number.
Expected integer.
It is expected a positive integer.
The value should be in the range of [%1 .. %2]
The ‘% 1’ is already present in the set of valid characters.
The field must be less than 1%.
The first character must be a letter of the Latin alphabet.
Su
Mo
Tu
We
Th
Fr
Sa
January
February
March
April
May
June
July
August
September
October
November
December
century
B.C.
%1 century
An error occurred while importing data on line% 1. Value: ‘%2’. Error: %3
Unable to determine the field separator. To separate fields, you can use the following characters: Tab, semicolon (;) or comma (,).
%3.%2.%1%4
%3.%2.%1%4 %6:%7
s.sh.
u.sh.
v.d.
z.d.
yes
no
Wrong file format. Only the following formats: %1
Please leave your phone number and / or email.
hostciti.net


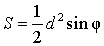
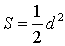
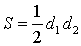
 Четырёхугольник — это фигура из четырёх точек (вершин), из которых любые три не лежат на одной прямой, и четырёх отрезков (сторон) последовательно их соединяющих.
Четырёхугольник — это фигура из четырёх точек (вершин), из которых любые три не лежат на одной прямой, и четырёх отрезков (сторон) последовательно их соединяющих.