Объем сосуда формула: Как определить объём сосуда 🚩 формула объема сосуда 🚩 Математика

3$ — эта запись означает, что объём некоторого сосуда равен 3-м, если в качестве единицы измерения взят кубический миллиметр.

Основные свойства объёмов:

1. У равных сосудов равные объёмы.
2. В случае, когда сосуд состоит из нескольких сосудов, то его объём равен сумме всех этих сосудов.

Эти свойства аналогичны свойствам длин отрезков и площадей многоугольников.

Часто требуется найти объём параллелепипеда, пирамиды, цилиндра, конуса и шара. Параллельно с формулами объёма дадим ключевые определения. Чтобы рассмотреть такую фигуру как параллелепипед, необходимо дать два важных определения:

1. Многогранник — это тело, ограниченное несколькими многоугольниками (гранями). Стороны граней называют рёбрами, а концы рёбер — вершинами.
2. Призма — это многогранник, который составлен из двух параллельных многоугольников (оснований призмы), вершины которых соединены параллельными и равными друг другу отрезками (боковыми ребрами призмы), образующими параллелограммы (боковые грани призмы).

Готовые работы на аналогичную тему

Нахождение объёма параллелепипеда

Параллелепипед — это многогранник, составленный из 6-ти прямоугольников. Или это четырёхугольная призма, в которой основания — параллелограммы. Форму параллелепипеда имеют коробки, комнаты и многие другие предметы из нашей повседневной жизни.

В случае, когда у параллелепипеда боковые ребра перпендикулярны к плоскостям оснований, а боковые грани и основания — прямоугольники, то этот параллелепипед называют прямоугольным (прямым).

Для нахождения объёма прямоугольного параллелепипеда необходимы его измерения. Измерения параллелепипеда — это длины трёх рёбер с общей вершиной. В речи мы называем измерениями «длину», «ширину» и «высоту» (например, при измерении комнаты).

Определение 1

Объём прямоугольного параллелепипеда равен произведению трёх его измерений: $V=abc$.

Если площадь основания $S=ac$, а высота $h=b$, то формула объёма может быть следующей: $V=Sh$.

Нахождение объёма пирамиды

Пирамида — это многогранник, образованный из $n$-угольника (в качестве основания) и треугольников (в качестве боковых граней), построенных путем соединения одной точки (вершины пирамиды) отрезками (боковыми рёбрами) с вершинами многоугольника.

Рисунок 1. Пирамида. Автор24 — интернет-биржа студенческих работ

Определение 2

Объём пирамиды равен одной трети произведения площади основания на высоту. В данном случае высота представляет собой перпендикулярный к плоскости основания отрезок, который соединяет вершину пирамиды с плоскостью её основания.

$V=\frac{Sh}{3}$.

Нахождение объёма цилиндра

Цилиндр — некоторое тело (или сосуд), полученное в результате вращения некоторого прямоугольника вокруг своей оси (одной из сторон прямоугольника).

Рисунок 2. Цилиндр. Автор24 — интернет-биржа студенческих работ

Определение 3

Объём цилиндра равен произведению площади основания на высоту: $V=Sh$.

3$, где $R$ — радиус шара.

Таким образом, мы перечислили все основные формулы объёма основных фигур в стереометрии.

Формулы объема и программы для расчета объема

Содержание:

Объём геометрической фигуры — количественная характеристика пространства, занимаемого телом или веществом. В простейших случаях объём измеряется числом умещающихся в теле единичных кубов, т. е. кубов с ребром, равным единице длины. Объём тела или вместимость сосуда определяется его формой и линейными размерами.

Формула объема куба

1) Объем куба равен кубу его ребра.

V — объем куба

H — высота ребра куба

См. также: Программа для расчета объема куба.

Формула объема пирамиды

1) Объем пирамиды равен одной трети произведения площади основания S (ABCD) на высоту h (OS).

V — объем пирамиды

S — площадь основания пирамиды

h — высота пирамиды

См. также: Программа для расчета объема пирамиды.

Формулы объема конуса

1) Объем конуса равен одной трети произведения площади основания на высоту.

2) Объем конуса равен одной трети произведения числа пи (3.1415) на квадрат радиуса основания на высоту.

V — объем конуса

S — площадь основания конуса

h — высота конуса

π — число пи (3.1415)

r — радиус конуса

См. также: Программа для расчета объема конуса.

Формулы объема цилиндра

1) Объем цилиндра равен произведению площади основания на высоту.

2) Объем цилиндра равен произведению числа пи (3.1415) на квадрат радиуса основания на высоту.

V — объем цилиндра

S — площадь основания цилиндра

h — высота цилиндра

π — число пи (3.1415)

r — радиус цилиндра

См. также: Программа для расчета объема цилиндра.

Формула объема шара

1) Объем шара вычисляется по приведенной ниже формуле.

V — объем шара

π — число пи (3.1415)

R — радиус шара

См. также: Программа для расчета объема шара.

Формула объема тетраэдра

1) Объем тетраэдра равен дроби в числителе которой корень квадратный из двух помноженный на куб длины ребра тетраэдра, а в знаменателе двенадцать.

V — объем тетраэдра

a

— длина ребра тетраэдра

См. также: Программа для расчета объема тетраэдра.

Слишком сложно?

Формулы объема не по зубам? Тебе ответит эксперт через 10 минут!

Способ измерения объема сосуда и устройство для его осуществления

Способ измерения объема сосуда заключается в том, что изменяют объем сосуда на величину ΔV и определяют изменение давления газа в сосуде до и после изменения объема, на основании которых определяют искомый объем сосуда V₀. При этом предварительно выравнивают давление в герметично закрытом сосуде с окружающей средой. Перемещением стержня изменяют его объем на величину ΔV

1 и измеряют давление ΔP₁ внутри сосуда по отношению к внешней среде. Затем убеждаются, что оно не изменяется с течением времени. Изменяют объем сосуда на величину ΔV, выравнивают давление в сосуде с окружающей средой, повторно изменяют объем сосуда на величину ΔV₂, измеряют давление ΔР₂ внутри сосуда по отношению к внешней среде и повторно убеждаются, что оно не изменяется с течением времени. Искомый объем сосуда V₀ определяют по формуле: V₀=(ΔV·k·ΔP₂/ΔV₂)/(ΔP₂/ΔV₂-ΔP₁/ΔV₁), где k=1, если объем сосуда уменьшают и k=-1, если увеличивают. Устройство для измерения объема сосуда содержит толстостенную крышку, в которой выполнено отверстие. В отверстии установлено уплотнительное кольцо и цилиндрический стержень, выполненный с возможностью его вращения и осевого перемещения его цилиндрической части в нижней части отверстия. В крышке выполнены первый и второй сквозные каналы, входы которых расположены на внутренней стороне крышки. На крышке установлены устройство поворота стержня на заданный угол и запорный клапан, перекрывающий соединение первого канала с атмосферой. К выходу второго канала подключен первый вход дифференциального датчика давления, второй его вход сообщается с атмосферой, а его выход и выход устройства поворота соединены с устройством расчета объема. Технический результат — повышение точности измерения объема сосуда. 2 н. и 1 з.п. ф-лы, 1 ил.

 

Изобретение относится к неразрушающим методам измерения и может быть использовано для измерения в воздушной среде объема внутренней полости сосуда, имеющей сложную геометрическую форму в различных отраслях машиностроения, автомобилестроения, горной и ювелирной промышленностях.

Согласно «РД 26-18-89 Сосуды. Термины и определения», сосуд — это изделие (устройство), имеющее внутреннюю полость, предназначенное для ведения химических, тепловых и других технологических процессов, а также для хранения и транспортирования газообразных, жидких и других веществ.

Необходимость измерения объема сосудов, внутренняя полость которых имеет сложную геометрическую форму, возникает при решении двух задач. Первая задача заключается в измерении объемов V₀ однотипных сосудов, имеющих сложную форму, формируемую при их изготовлении, например, — нестандартных сосудов, заготовок камер сгорания двигателя и других, с целью их сравнения с требуемым (эталонным) значением на соответствие полю допусков. Вторая задача заключается в определении объема V_m твердого тела (не сжимаемого при изменении атмосферного давления), имеющего сложную форму, например, — ювелирного изделия, образца горной породы, и др. с тем чтобы, зная его массу, рассчитать плотность материала, из которого он изготовлен. Для этого его помещают в сосуд с известным значением объема V _u, определяют разницу V₀ между двумя этими объемами, по которой и вычисляют V_m=V_u-V₀. В обеих задачах измеряется объем сосуда V₀, только в первом случае он имеет сложную форму из-за его внутренней геометрии, а во втором — из-за объекта, помещаемого в известный объем. Как будет видно из дальнейшего, заявляемое изобретение позволяет решить обе эти задачи.

Самый распространенный способ измерения объема заключается в замещении искомого объема жидкостью (вода, масло) с последующим измерением ее объема мерником, в качестве которого используется измерительная колба, бюретка, цилиндр, мензурка и др. (Гаузнер С.И., Кивилис С.С., Осокина А.П., Павловский А.Н. Измерение массы, объема и плотности. М.: Издательство стандартов. 1972. 623 с.). Его главный недостаток заключается в том, что сосуд наполняется жидкостью. Это приводит к необходимости очищать сосуд от жидкости после измерений, что увеличивает погрешность измерений, поскольку не вся жидкость измеряется мерником — часть остается на стенках сосуда. Кроме того, наличие процедуры наполнения и удаления жидкости из сосуда усложняет и увеличивает длительность проведения измерений. Очевидно также, что способ имеет ограниченные возможности для применения, поскольку может использоваться только для тех сосудов, и помещенных в них твердых тел, для которых контакт с жидкостью не наносит вредных последствий в виде впитывания в поверхность, набухания, растворения, коррозии, засорении микропор и др. . Определенным недостатком способа является невозможность его применения в условиях поточного, производственного контроля, когда требуется высокая производительность измерений и время на проведение измерений ограничено.

Для устранения указанных недостатков проведение измерений объема необходимо осуществлять в воздушной среде. Зависимость давления P от объема V описывается уравнением состояния идеального газа Клапейрона-Менделеева: PV=(M/µ)RТ, где: M — масса газа, µ — молярная масса газа, R — универсальная газовая постоянная, Т — абсолютная температура (Физическая энциклопедия. Т.2. Под ред. А.М. Прохорова. — М.: Советская энциклопедия. 1990. с.371). Из него следует, что по изменению давления для различных объемов можно рассчитать и величину объема искомого сосуда. Сложность решения этой задачи заключается в том, что в процессе измерений могут изменяться условия ее проведения: газовый состав среды (M/µ), температура (T), условия соблюдения герметичности сосуда (приводит к изменению давления во времени), что для обеспечения прецизионных измерений требует их непрерывного контроля с целью учета в формуле для расчета объема. Естественно, что большое количество измеряемых параметров усложняет процедуру определения объема и неизбежно приводит к увеличению погрешности измерений. В известных способах измерения объема пытаются сохранить компромисс между соблюдением неизменности параметров среды в процессе измерений и.минимизацией числа датчиков для изменения параметров, необходимых для расчета объема, что не всегда удается.

Известны технические решения, позволяющие определять объем тел в воздушной среде.

Известен ряд способов измерения объема сосудов в различных вариантах исполнения, основанных на измерении резонансной частоты сосуда (пат. RU 2131590, публ. 10.06.1999, МПК⁶ G01F 23/28; пат. USA 4,640,130, публ. 03,02,1987, МПК⁴ G01N 29/00, G01F 17/00; пат. USA 7,578,183, публ. 25.08.2009, МПК⁷ G01F 23/28, G01F 17/00), частично решающих поставленную задачу, поскольку они позволяют определять объем сосудов в воздушной среде. Сущность способов заключается в том, что в измеряемом объеме сосуда возбуждают акустические колебания с частотой, равной резонансной частоте измеряемого объема, по значению которой по определенным формулам рассчитывают значение объема. Недостатками способов являются сложность их технической реализации и низкая точность измерений для сосудов сложной формы. Зависимость объема от частоты, даже в простейшем случае для резонатора Гельмгольца имеет сложный вид. Так, например, для сферического сосуда с горлышком объем определяется по формуле: V=S/[(2µf)²ρβL], где: ρ, β — плотность и сжимаемость среды; S, L — площадь сечения и длина горлышка (Исакович М.А. Общая акустика. Учебное пособие. — М.: Наука. 1973. с.370-374). То есть, зависимость объема от частоты носит квадратичный, нелинейный характер и ошибка в определении частоты при расчете объема будет многократно увеличена. Достаточно точно значение частоты можно измерить только для сосудов сферической формы, имеющих высокую добротность. Для сосудов, имеющих сложную форму, добротность будет мала и, следовательно, точность определения резонансной частоты будет низка, поскольку максимум колебаний будет иметь «плоскую» форму. Кроме того, для расчета объема дополнительно необходимо знать плотность среды, которая зависит от температуры и состава газов. Априорно они не известны и их определение в указанных способах не предусмотрено, что создает неопределенность в выборе их значений для проведения расчета объема и снижает достоверность измерений. Для возбуждения акустических колебаний в измерительном объеме в способе подразумевается размещение акустического элемента возбуждения (громкоговорителя). При его работе, из-за наличия активного сопротивления обмоток возбуждения будет происходить их нагрев, что приведет и к изменению температуры окружающего воздуха. Поскольку она не контролируется и не учитывается, то это также приведет к увеличению погрешности вычисления объема. Действие указанных факторов приводит к тому, что этот способ имеет низкую точность измерений, поскольку объем сложным образом зависит от частоты, зависит от температуры, которая не контролируется и может изменяться вследствие работы возбудителя акустических колебаний. Кроме того, способ имеет низкую производительность измерений, поскольку для определения резонансной частоты необходимо перестраивать частоту возбуждения акустических колебаний с определенным шагом в определенном диапазоне частот, а после каждого шага еще и необходимо ожидать некоторое время для окончания процесса установления резонансных колебаний, что существенно увеличивает длительность процедуры определения значения резонансной частоты и снижает производительность измерений.

Известен ряд способов определения объема в замкнутых емкостях большого размера, основанных на измерении параметров истекаемого газа (пат. RU 2079112, публ. 10.05.1997, МПК⁶ G01F 17/00; пат. SU 1536209, публ. 15.01.1990, МПК⁶ G01F 17/00; пат. RU 2217721, публ. 27.11.2003, МПК⁷ G01M 3/26, G01F 17/00; пат. RU 2292536, публ. 27.01.2007, МПК⁷ G01M 3/26, G01F 17/00), частично решающих поставленную задачу, поскольку они позволяют измерять объем сосудов сложной формы в воздушной среде. Сущность способов заключается в наддуве емкости избыточным давлением, измерении в ней давления и температуры, осуществлении истечения воздуха через калиброванные течи, определении интервалов времени падения давления и расчете на основе измерения времен, давлений и температур объема емкости. Недостатком способов является их ограниченное использование только для объемов большой емкости, а также низкая точность измерения, обусловленная тем, что формулы для расчета объема достаточно сложны, зависят от многих параметров, а зависимость объема от времени падения давления нелинейна. Недостатком способов также является длительность процедуры измерения, заключающаяся в необходимости использования процедуры наддува воздуха, контроля герметичности при высоких давлениях и выпускания воздуха через калиброванные течи, для определения параметров которых, кроме того, требуется проведение дополнительных испытаний течи с эталонным объемом и известным составом воздушной среды, имеющими характеристики близкие к измеряемым. За время измерений параметры воздушной среды, в частности, — ее температура, могут измениться, быть неравномерно распределенными внутри объекта большого объема, что меняет условия истечения и вносит неконтролируемую погрешность в результат измерения.

Известен способ определения объема мостового типа, основанный на сравнении параметров измеряемого и эталонного объемов (пат. USA 4,561,298, публ. 31.12.1985, МПК⁴ G01F 17/00), частично решающий поставленную задачу, поскольку позволяет измерять объем сосуда сложной формы с высокой чувствительностью, заключающийся в сравнении давлений в исследуемом объеме и эталонном, для чего в обоих объемах создается переменное давление, определяются амплитуды давлений в каждом объеме и по ним рассчитывается значение искомого объема. Главным недостатком этого способа является низкая точность измерений, обусловленная тем, что состав воздушной среды и ее температура в обоих объемах не контролируются и могут быть различны. Несмотря на высокую чувствительность мостового способа, в данном случае сравниваются давления для различных исходных значений состава воздуха и температуры, которые соответствуют другим условиям состояния и объемам в уравнении Клайперона-Менделеева, что приводит к значительной погрешности измерения искомого объема.

Наиболее близким по технической сущности и достигаемому эффекту является способ измерения объема жидкости в сосуде (пат. RU 2344380, публ. 20.01.2009, МПК⁷ G01F 23/00), позволяющий измерять объем сосуда сложной формы в воздушной среде, который выбран в качестве ближайшего аналога.

Этот способ измерения объема жидкости V₀ заключается в том, что увеличивают объем газа в исследуемом сосуде объемом V на величину ΔV путем уменьшения объема жидкости, заполняющей его, измеряют давление газа до и после увеличения объема и определяют объем жидкости по формуле: V₀=V-ΔV·P₁/(P₀-P₁), где Р₀, P₁ — давление газа в сосуде до и после изменения объема жидкости на величину ΔV. Его основным недостатком является низкая точность измерения, поскольку для расчета используются абсолютные значения давления газа, отсутствует контроль герметичности сосуда, а для изменения объема сосуда используется жидкость. Абсолютное значение давления газа зависит от многих факторов, которые постоянно изменяются, поэтому для получения высокой точности измерений его нужно определять точно и непосредственно перед проведением измерений путем его калибровки по эталонному устройству, что усложняет способ и увеличивает продолжительность проведения измерений. Кроме того, поскольку на практике значение разности давлений P₀-P₁ существенно меньше, чем значение Р₀, то погрешность измерения будет тем больше, чем она меньше. Это означает, что для высокой точности измерений способ должен использоваться при таких измерениях объема ΔV, которые приводят к изменению разности давлений P₀-P₁, сравнимой по величине с давлением P₀. То есть, для получения высокой точности измерения в способе прототипе необходимо изменить объем на значительную величину ΔV, что требует перетекания большого объема жидкости и увеличивает общее время проведения измерений, в течение которого сосуд должен быть герметично закрыт. Кроме того, в процессе проведения измерений из-за понижения давления на значительную величину может быть нарушена герметичность сосуда, которая в данном способе не контролируется, что приведет к недостоверным измерениям давления и, следовательно, к ошибке в расчете объема сосуда. Недостатком способа является также то, что измерение объема осуществляется путем изменения объема жидкости, присутствующей в сосуде. Жидкость постоянно испаряется и изменяет состав газа и температуру при различных давлениях, что изменяет условия измерения давления до и после изменения объема на величину ΔV, и приводит к увеличению погрешности измерений. К недостаткам способа также относится наличие процедур перемещения жидкости из исследуемого сосуда с помощью компрессора и измерения ее объема мерной емкостью, что существенно усложняет способ измерения, а также увеличивает продолжительность измерений.

Задачей изобретения является создание простого и производительного способа измерения объема сосуда в воздушной среде, имеющего сложную форму, при одновременном увеличении точности измерений.

Техническим результатом изобретения в части способа является снижение времени определения объема сосуда при одновременном увеличении точности, за счет использования дозированного метода изменения объема и контроля герметичности закрытия сосуда.

Технический результат, в части способа достигается тем, что в способе измерения объема сосуда, включающем изменение объема сосуда на величину ΔV и определение изменения давления газа в сосуде до и после изменения объема, на основании которых определяют искомый объем сосуда V₀, согласно изобретению, предварительно выравнивают давление в герметично закрытом сосуде с окружающей средой, перемещением стержня изменяют его объем на величину ΔV₁ и измеряют давление ΔP₁ внутри сосуда по отношению к внешней среде, убеждаются что оно не изменяется с течением времени, изменяют объем сосуда на величину ΔV, выравнивают давление в сосуде с окружающей средой, повторно изменяют объем сосуда на величину ΔV₂, измеряют давление ΔP₂ внутри сосуда по отношению к внешней среде, и повторно убеждаются что оно не изменяется с течением времени, а объем определяют по формуле: V₀=(ΔV·k·ΔP₂/ΔV₂)/(ΔP₂/ΔV₂-ΔP₁/ΔV₁), где: k=1, если объем сосуда уменьшают и k=-1, если увеличивают.

Для достижения технического результата в части способа в данном изобретении используется эффект постоянства сжимаемости газа при постоянном давлении и температуре. Как известно, сжимаемостью газа называется его способность уменьшать свой объем под действием сил внешнего давления (Загузов И.С., Поляков К.А. Математические модели в аэрогидромеханике. Ч.1: Учебное пособие. Самара: Изд-во «Самарский университет», 2001. С.15.; Корнфельд М. Методы и результаты исследования объемной упругости вещества // Успехи физических наук. 1954. Т.LIV, вып.2. С.315-342). Мерой сжимаемости является модуль объемной упругости Е, определяемый из равенства E=-ΔP/(ΔV₀/V₀), где ΔV₀/V₀ — относительное изменение объема, вызванное повышением давления на величину ΔP. При небольших изменениях давления изменение объема ΔV₀ пропорционально изменению давления ΔP. Модуль объемной упругости зависит от состава газовой среды и температуры, которые, в отличие от прототипа, в предлагаемом способе не изменяются. Тогда определить объем сосуда можно следующим образом. Модуль объемной упругости для искомого объема V₀ и этого же объема, измененного на величину ΔV одинаков, тогда: Е=-ΔP₁·V₀/ΔV₁=-ΔP₂(V₀-ΔV·k)/ΔV₂, где ΔV₁, ΔV₂<ΔV и ΔP₁, ΔP₂ — изменения объема и соответствующие им изменения давления, k — коэффициент, учитывающий направление изменения объема (k=1, если объем сосуда уменьшают на величину ΔV и k=-1, если увеличивают). Отсюда, в общем случае получаем, что V₀=(ΔV·k·ΔP₂/ΔV₂)/(ΔP₂/ΔV₂-ΔP₁/ΔV₁). Это равенство можно упростить, если модуль E определять при одинаковых изменениях объема, т.е. ΔV₁=ΔV₂, что технически более просто, чем зафиксировать изменение давления (ΔP₁=ΔP₂) и измерять изменение объема, и формула упрощается до вида: V₀=ΔV·k·ΔP₂/(ΔP₂-ΔP₁)=ΔV·k·/(1-ΔP₁/ΔP₂).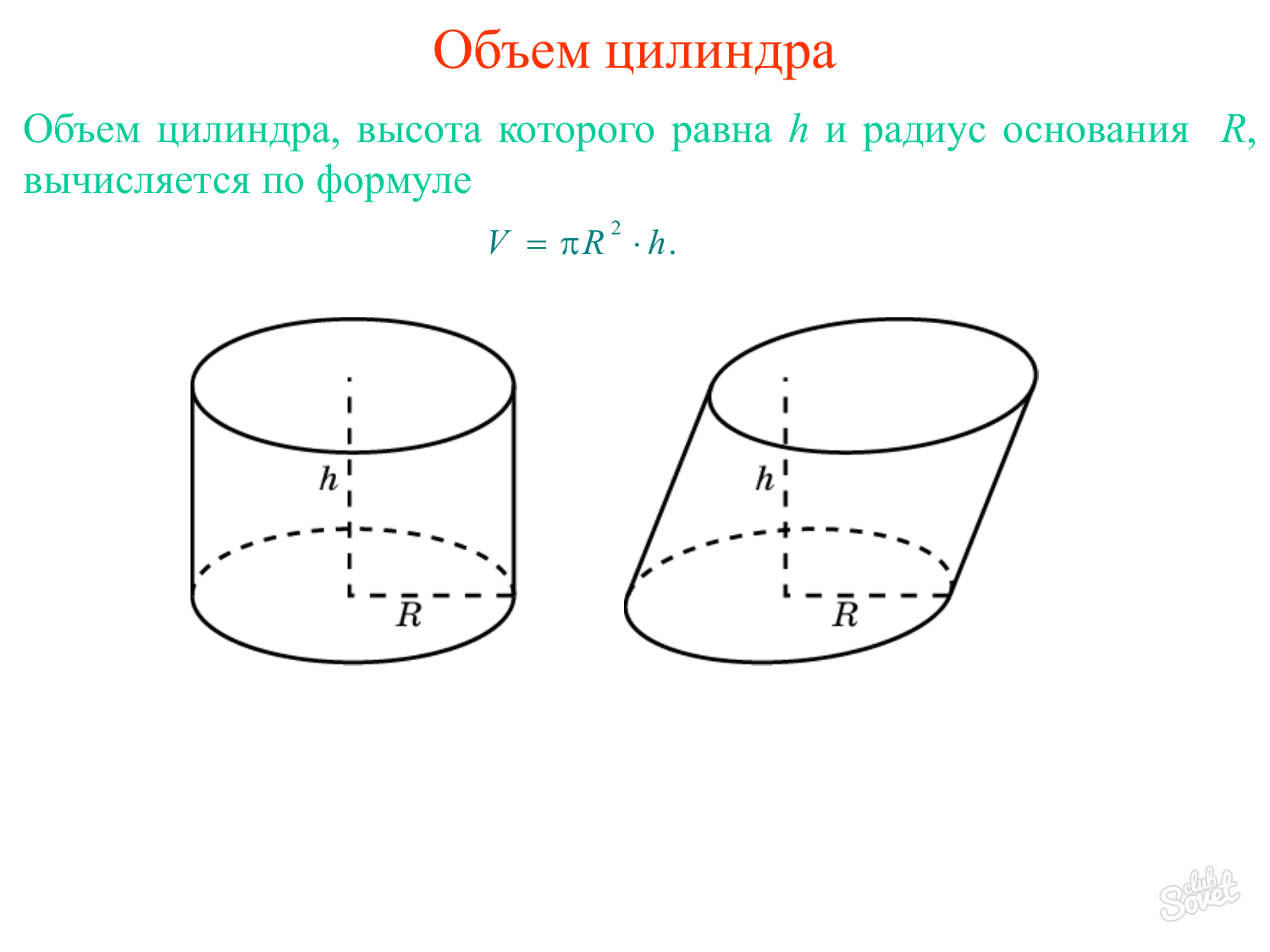

Изменение объемов сосуда на величину ΔV₁, ΔV₂, ΔV осуществляется путем введения (или выведения) в полость сосуда стержня на фиксированную величину с помощью механической, например, — винтовой передачи. При этом перемещение может осуществляться или рукой, или с помощью шаговых двигателей, что позволяет изменять объем достаточно быстро, просто и на величину, достаточную для проведения точных измерений создаваемых им давлений, что существенно упрощает и ускоряет способ проведения измерений. Изготовленный из металла стержень сохраняет форму, не изменяет свой объем со временем. Кроме того, объем, изменяемый им, поддается расчету, допускает многократное применение и не требует постоянного контроля, что выгодно отличает его использование от употребления мерников с жидкостью. Это позволяет заранее подготовить и выбрать величину изменяемого объема и не контролировать его изменение в процессе измерений, что экономит время в процессе проведения измерений. Поскольку изменение объемов с помощью стержня приводит к изменению давлений ΔP₁ и ΔP₂ на небольшие величины, это значительно снижает требования к герметичности закрытия сосуда, что существенно по сравнению с прототипом упрощает устройство его закрытия и герметизации. Достоинством способа является также то, что одновременно с измерением давления осуществляется контроль герметичности сосуда: если давления ΔP₁, ΔP₂ не изменяются в течение нескольких секунд, то сосуд закрыт герметично и измеренные значения следует считать достоверными. Причем, герметичность закрытия сосуда не должна соблюдаться в течение всего времени проведения измерений, как в прототипе, а только на период изменения объема на величины ΔV₁, ΔV₂ и определения создаваемого ими давлений, что существенно увеличивает достоверность измерений. Поскольку для расчета объема используются не абсолютные значения давления, а изменения давления ΔP₁, ΔP₂ относительно окружающей среды (относительно атмосферного давления), специально создаваемые путем изменения искомого объема на небольшие величины ΔV₁, ΔV₂, то для этого используются датчики не абсолютного давления, как в прототипе, а дифференциальные. Очевидно, что относительные измерения давления, осуществляемые в данном способе дифференциальным способом, можно выполнить с более высокой точностью и чувствительностью, что позволяет не только обеспечить высокую точность измерения давлений, но и по их малейшему изменению контролировать герметичность закрытия сосуда, что не достижимо в прототипе. При этом существующее значение атмосферного давления не влияет на результат измерений и не подлежит измерению, что упрощает процесс измерения, поскольку не требуется проведение абсолютных измерений. Поскольку при герметичном закрывании сосуда давление в нем может измениться, например, за счет продавливания крышки сосуда в его горловину вследствие упругости ее контакта, обеспечивающего герметизацию, то перед изменением объема давление в сосуде необходимо выровнять с окружающей средой. Для этого внутренняя полость сосуда через канал кратковременно соединяется с внешней средой. Контроль выравнивания давления осуществляется по датчику давления — его показание становится равным нулю. Это же условие необходимо выполнить и для сосуда с объемом, измененным на величину ΔV. Его выполнение обеспечивает равенство условий измерений упругости воздуха в сосуде для двух значений объемов и одинаковый состав воздушной среды и температуры. Таким образом, повышение точности обеспечивается, как точным изменением объема за счет перемещения стержня, контролем герметичности сосуда по изменению уровня давления, создаваемого им, и дифференциальным способом измерения давления за счет его более высокой чувствительности. Другим достоинством заявляемого способа является возможность проведения многократных измерений ΔP₁ и ΔP₂ путем периодического изменения ΔV₁, ΔV₂, поскольку технически это выполняется просто и быстро путем введения и выведения в исследуемый объем стержня. Накапливание и последующее усреднение результата измерения ΔP₁ и ΔP₂ также позволяет снизить погрешность измерения исследуемого объема.

Дополнительный технический результат в первом частном случае реализации способа, заключается в дополнительном увеличении точности измерений.

Дополнительный технический результат достигается за счет того, что перед проведением измерений величину измеряемого объема V уменьшают путем введения в сосуд твердого тела с известным объемом ΔV’, а истинный объем определяют как сумму измеренного V₀ и введенного в сосуд объемов: V=V₀+ΔV’. Из используемой для расчета объема сосуда формулы следует, что для измерения объема с высокой точностью, например, менее процента, необходимо, чтобы значения ΔP₁ и ΔP₂ измерялись с точностью не ниже требуемой. На практике, при измерении объемов значительной величины, для достижения нужных (регистрируемых с необходимой чувствительностью и точностью) значений давлений потребуется изменять ΔV₁, ΔV₂ на значительные величины. Это технически усложняет способ, поскольку потребует введения-выведения в исследуемый объем стержня или стержня большого объема. Для того, чтобы не увеличивать значения этих объемов и проводить измерения при малых значениях изменения ΔV₁, ΔV₂, что упрощает и ускоряет процесс измерений, поскольку изменять объем на малые величины технически более просто, чем на большие, следует изначально уменьшить измеряемый объем V на известную величину ΔV’. Для этого достаточно ввести в него этот объем изначально и измерять разницу V₀=V-ΔV’ между измеряемым объемом и введенным. Поскольку измеряемый объем V₀ будет меньше исходного, то изменения объемов ΔV₁, ΔV₂ приведут к существенно большим изменениям давлений ΔP₁, ΔP₂, что можно будет измерить с более высокой точностью и этим самым повысить точность определения искомого объема значительной величины.

Известен ряд устройств измерения объема сосудов в различных вариантах исполнения, основанных на измерении резонансной частоты сосуда (пат. RU 2131590, публ. 10.06.1999, МПК⁶ G01F 23/28; пат. USA 4,640,130, публ. 03,02,1987, МПК⁴ G01N 29/00, G01F 17/00; пат. USA 7,578,183, публ. 25.08.2009, МПК⁷ G01F 23/28, G01F 17/00), частично решающих поставленную задачу, поскольку позволяют определять объем сосудов в воздушной среде. Устройства в общем случае содержат возбудитель и датчик акустических колебаний, размещенные в измеряемом сосуде, блок измерения частоты и устройство для проведения вычислений объема. Недостатком устройств является сложность их практической реализации, длительность процедуры измерения и низкая точность при измерении сосудов сложной геометрической формы. Сложность практической реализации обусловлена использованием значительного количества сложных электронных приборов и акустических элементов: перестраиваемого генератора, частотомера, усилителя мощности с возбудителем акустических колебаний, датчика акустических колебаний с предусилителем. Для определения резонансной частоты необходимо перестраивать генератор с малым шагом (чем меньше, тем лучше), что увеличивает общее время ее определения до единиц минут. Кроме того, для сосудов сложной формы, имеющих низкую добротность, частота будет определяться с большой погрешностью. Дополнительным фактором, усложняющих реализацию устройства на практике является необходимость принятия мер для исключения прохождения акустических колебаний непосредственно по корпусу сосуда с возбудителя (излучателя) колебаний на принимающий их датчик. Это обусловлено тем, что все они механически связаны (закреплены на общем основании), в результате этого вибрации излучателя обязательно по механическим соединениям или корпусу неконтролируемо попадут на принимающий датчик, где сложатся с сигналом полезного сигнала, полученного через воздушную среду, изменят его уровень и, следовательно, ухудшат точность измерения его амплитуды. Акустическая развязка возбудителя и приемника от поверхности объекта, заключающаяся в использовании виброизолирующих и поглощающих звук прокладок, существенно усложняет практическую реализацию устройства. Работающий возбудитель звука из-за наличия потерь в обмотках возбуждения в процессе работы будет нагреваться, что приведет к непрерывному изменению температуры внутри сосуда и, следовательно изменению его резонансной частоты, связанной не с изменением его объема, а с изменением свойств заполняющей его среды, что требует учета, но практически не выполняется. Поскольку в предложенных устройствах измерение температуры не предусмотрено, то работа возбудителя приведет к неконтролируемому изменению температуры и, следовательно, к большим погрешностям определения частоты и вычисления по ней объема.

Известно устройство мостового типа для измерения объема (пат. USA 5,824,892, публ. 20.10.1998, МПК⁶ G01F 17/00), частично решающее поставленную задачу, поскольку позволяет определить объем сосуда в воздушной среде с высокой чувствительностью. Устройство состоит из измеряемого и эталонного контейнеров, разделенных мембраной (прокладкой), соединенной с громкоговорителем, предназначенным для создания переменного давления, двух микрофонов, размещенных в контейнерах для измерения давления, и электронного блока для расчета измеряемого давления в зависимости от давлений в контейнерах. Главным недостатком этого устройства является низкая точность измерений, связанная с тем, что состав воздушной среды и ее температура в обоих контейнерах не контролируются и, следовательно, может быть различна. Размещение громкоговорителя внутри контейнеров приведет к изменению температуры вблизи него вследствие его нагрева в процессе работы, что создаст неравномерное распределение температуры внутри измеряемых объемов. В результате, несмотря на высокую чувствительность мостового способа измерений, сравниваться будут два объема с разными свойствами среды внутри них, что не позволяет правильно вычислить объем исследуемого контейнера по измеренным давлениям в контейнерах, и приведет к большой погрешности измерения. Недостатком этого устройства также является сложность технической реализации, заключающаяся в использовании значительного числа акустических элементов и аппаратуры: источника переменного давления, громкоговорителя, двух микрофонов в эталонной и измерительной камерах. Необходимость крепления и акустической изоляции указанных элементов внутри камер, учета занимаемого ими объема, необходимость наличия эталонного контейнера, близкого по своей геометрии к исследуемому приводит к усложнению конструкции измеряемого устройства и ограничивает область его применения на практике только решением частной задачи.

Известно устройство мостового типа для измерения внутреннего объема сосуда, основанное на сравнении резонансных частот измеряемого и эталонного объемов (пат. RU 2042927, публ. 27.08.1995, МПК⁶ G01F 17/00), позволяющее частично решить поставленную задачу, поскольку позволяет измерять объем сосуда в воздушной среде с высокой чувствительностью. Это устройство содержит излучатель звука и установленный в измеряемом сосуде приемник звука, дополнительную камеру с двумя противоположно расположенными отверстиями одинаковых размеров, одно из которых соединено с горловиной измеряемого сосуда, а второе сообщено с атмосферой, и дополнительным приемником звука, установленным в камере, при этом излучатель звука сообщен с камерой. Такое конструктивное выполнение устройства позволяет снизить погрешность измерения, вызываемую колебаниями температуры измеряемого сосуда относительно температуры окружающей среды, благодаря тому, что измерения резонансных частот проводят одновременно для двух колебательных систем (в объеме измеряемого сосуда и в отверстиях камеры), для которых предполагается, что состав воздуха и температура одинаковы. Однако, на практике без принудительной вентиляции воздуха по обоим объемам температура и состав воздуха в них будут различны, что нарушает исходные условия для этой схемы измерения. В результате будут сравниваться объемы с разным составом воздушной среды и, в значительной степени, — температуры. Если же предположить, что условия в обеих объемах станут одинаковыми за счет естественного теплообмена и циркуляции воздуха, то этот процесс займет продолжительное время, что снизит производительность измерений устройства. К тому же этот процесс теплообмена в устройстве не контролируется, что создает неопределенность в определении времени, по истечении которого можно считать, что состав воздушной среды и температура стали одинаковыми, что снижает достоверность проводимых измерений. Кроме того, как отмечено выше, измерение резонансной частоты с высокой точностью возможно только для объектов правильной шаровидной формы, которые в камере данного устройства не используются, а используется более простая форма — цилиндрическая. Измерение же резонансных частот цилиндрических отверстий и объектов сложной формы, имеющих низкую добротность, приведет к значительным погрешностям измерения. К недостаткам устройства также относится продолжительность процедуры измерения, поскольку для расчета объема необходимо измерять две резонансные частоты. Определенным неудобством использования устройства является то, что для увеличения точности измерений объем эталонной камеры должен быть близок к измеряемому, что для различных объемов требует создания целого набора эталонных камер.

Известен ряд устройств определения объема в замкнутых емкостях большого размера, основанных на измерении параметров истекаемого газа (пат. RU 2079112, публ. 10.05.1997, МПК⁶ G01F 17/00; пат. SU 1536209, публ. 15.01.1990, МПК⁶ G01F 17/00; пат. RU 2217721, публ. 27.11.2003, МПК⁷ G01M 3/26, G01F 17/00; пат. RU 2292536, публ. 27.01.2007, МПК⁷ G01M 3/26, G01F 17/00), частично решающих поставленную задачу, поскольку позволяют измерять объем сосудов сложной формы в воздушной среде. Эти устройства содержат средство подачи в емкость воздуха с избыточным давлением, сопло с калиброванным сечением для истечения из емкости воздуха с избыточным давлением, датчик избыточного давления, а также таймер времени истечения воздуха из емкости, датчик атмосферного давления, датчик температуры воздуха в емкости и вычислитель объема замкнутой емкости. Главным недостатком устройств является сложность практической реализации и аппаратурного оформления, заключающиеся в необходимости использования большого количества датчиков, компрессора сжатого воздуха, выполнении требований к герметичности устройства впуска-выпуска воздуха при высоких давлениях, необходимости проведения калибровочных измерений для используемого диаметра сопла и, как следствие, — низкой точности измерений, в том числе из-за сложной формулы для расчета. Другим недостатком устройства является длительность процедуры измерения, определяемая как временем нагнетания и истечения газа, так и необходимостью проведения предварительных калибровочных измерений с используемым составом и температурой газа. Эти устройства имеют ограниченную область применения, поскольку могут быть использованы только для приблизительного определения значительных объемов типа цистерн, баков и т.п. сосудов.

Наиболее близким по технической сущности и достигаемому эффекту является устройство для измерения объема жидкости в сосуде (пат. RU 2344380, публ. 20.01.2009, МПК G01F 23/00), позволяющее измерять объемы сосудов сложной формы в воздушной среде, которое выбрано в качестве ближайшего аналога. Это устройство состоит из закрытого сосуда общим объемом V, в котором находится жидкость, имеющая объем V₀. Сосуд имеет сверху патрубок для налива жидкости. Патрубок герметично закрыт крышкой. Сверху сосуда также установлен манометр для измерения давления в воздухе над уровнем жидкости. В нижней части сосуда установлен патрубок с вентилем, к которому присоединен жидкостной насос. Для измерения объема жидкости ΔV, сливаемой из сосуда жидкостным насосом, служит мерная емкость. Недостатком устройства является сложность практической реализации и низкая точность измерений, обусловленная тем, что для изменения объема используется жидкость, а для ее перекачки — жидкостный насос.

Сложность практической реализации заключается в перекачивании жидкости из сосуда в мерную емкость с помощью насоса. Часть жидкости неизбежно остается на стенках мерной емкости, в узлах насоса и местах его соединения с сосудом, что приводит к погрешности истинного определения объема сливаемой жидкости и, следовательно, увеличению погрешности расчета объема сосуда. Кроме того, для каждого измерения необходимо наливать в сосуд жидкость жидкость, что усложняет проведение измерений, а для усреднения результатов измерения, с целью повышения достоверности и точности измерений, путем проведения нескольких измерений объема, эта процедура многократно увеличивает длительность проведения измерений. Использование жидкости для изменения объема сосуда приводит к увеличению погрешности измерений. Жидкость постоянно испаряется, изменяя свою температуру и окружающих ее узлов в зависимости от ее объема и занимаемой поверхности, которая к тому же для сложного сосуда при сливании жидкости будет изменяться, что делает температурный режим нестабильным и, следовательно, приводит к возрастанию погрешности измерения давления и вычисления объема сосуда. Использование для измерений манометра, позволяющего измерять абсолютные значения давлений, приводит к тому, что для повышения точности измерений необходимо изменять объем сосуда на величины, приводящие к изменениям давлений сравнимых с атмосферным, что увеличивает требования к герметичности закрытия сосуда, которые выполнить становится затруднительно. Герметичность не должна изменяться в течение всего длительного цикла проведения измерений, что усложняет реализацию устройства на практике. Причем на начальном этапе, до изменения объема, она не может быть проконтролирована, а значит в случае ее нарушения все последующие действия становятся бессмысленными. Определить герметичность по изменению давления можно только после изменения объема сосуда на определенную величину, то есть на заключительной стадии измерений. Отсутствие сведений о состоянии герметичности сосуда создает неопределенность в результативности проводимых измерений и их ненадежности. Если в конце измерений будет выяснено, что герметичность нарушена, то придется вернуть установку в исходное состояние — удалить часть жидкости, провести повторную герметизацию и повторить весь цикл измерений, что значительно увеличивает время для определения объема сосуда.

Техническим результатом изобретения в части устройства является упрощение аппаратурного оформления с одновременным сокращением времени измерений и повышением их точности.

Технический результат устройства достигается за счет того, что в устройстве для измерения объема сосуда, содержащем крышку, герметично подсоединенную к сосуду, и устройство для расчета объема сосуда по формуле, согласно изобретению, крышка выполнена толстостенной и содержит отверстие, в котором установлено уплотнительное кольцо, делящее его на верхнюю и нижнюю части, при этом верхняя часть отверстия имеет резьбу, цилиндрический стержень, установленный в отверстии и соединенный с крышкой посредством резьбового соединения, выполнен с возможностью его вращения и осевого перемещения его цилиндрической части в нижней части отверстия, на крышке закреплено устройство поворота стержня на заданный угол, в крышке выполнены первый и второй сквозные каналы, входы которых расположены на внутренней стороне крышки, на крышке установлен запорный клапан, перекрывающий соединение первого канала с атмосферой, при этом к выходу второго канала подключен первый вход дифференциального датчика давления, второй его вход сообщается с атмосферой, а его выход и выход устройства поворота соединены с устройством расчета объема.

Для достижения технического результата в части устройства в данном изобретении, изменение объема сосуда осуществляется путем введения (или выведения) части стержня из внутренней полости сосуда путем его вращения ручным или механическим способом в резьбовом соединении крышки сосуда. Для этого в крышке выполнено отверстие, для чего она должна иметь значительную толщину, достаточную для установления в ней стержня, уплотнительного кольца и выполнения в ней каналов. Для обеспечения изменения объема сосуда на заданную величину путем поворота стержня в части отверстия от верхней поверхности крышки до уплотнительного кольца, стержень имеет с крышкой резьбовое соединение. В нижней части отверстия стержень имеет цилиндрическую форму. Для герметизации соединения стержня с крышкой используется уплотнительное кольцо. Для поворота стержня относительно крышки на заданный угол, приводящий к изменению объема сосуда, используется поворотное устройство, снабженное маркерами угла поворота, установленными на крышке и стержне. Высокая точность изготовления шага резьбы позволяет точно определять по углу поворота стержня изменение его положения и, следовательно, изменяемый объем. Причем, в отличии от прототипа, это изменение может быть произведено одинаковым образом, многократно, за время порядка десятков секунд, что многократно увеличивает производительность измерений. Отсутствие компрессора и жидкости для измерения объема, существенно упрощают аппаратурное оформление устройства. Кроме того, поскольку изменения объема малы в сравнении с общим объемом сосуда, что необходимо выполнить для соблюдения постоянства упругости воздуха в сосуде от давления, то для измерения давления необходимо использовать дифференциальный датчик давления, позволяющий измерять разницу давлений между сосудом и окружающей средой с большей точностью и чувствительностью, чем в прототипе, что приводит к повышению точности измерений объема сосуда. Для измерения давлений в сосуде, создаваемых перемещением стержня, для различных значений объема сосуда используется дифференциальный датчик давления. Для обеспечения правильности его работы, перед процедурой перемещения стержня необходимо выравнивать давление в сосуде с атмосферой, для чего в крышке выполнен первый канал, выход которого перекрыт запорным клапаном. Этот же клапан, в положении «открыто» позволяет поддерживать давление в сосуде равным атмосферному во время изменении объема сосуда на величину ΔV, что позволяет избежать создания существенной разницы давлений между сосудом и атмосферой, как происходит в прототипе, и этим избежать неконтролируемого нарушения герметизации, повысить достоверность измерения давлений и, следовательно, точности определения объема сосуда. Второй канал, выполненный в крышке, соединяет первый вход дифференциального датчика с внутренним объемом сосуда, обеспечивая измерение давления в сосуде. При этом его второй вход соединен с атмосферой, а выход — с устройством расчета объема. Проведение измерений при малых изменениях давления, существенно упрощает требования к герметизации крышки сосуда, что упрощает и техническую реализацию устройства на практике. К устройству расчета объема так же подключен выход устройства поворота, что позволяет рассчитывать объем по приведенной в изобретении формуле. Дополнительным достоинством предлагаемого устройства является возможность полной автоматизации процесса измерения объема сосуда, за счет того, что перемещения стержня могут производиться под управлением микроконтроллера путем последовательного, в соответствии с процедурой измерения, вращения стержня на заданные углы с помощью шагового двигателя с одновременным открытием в нужные моменты времени запорного клапана, например, электро-магнитного типа, и измерения давлений, значения которых запоминаются, например, — с помощью аналого-цифрового преобразователя, после чего по исходным данным производится расчет объема сосуда.

На фиг.1 приведена схема разработанного устройства, реализующего разработанный способ измерения объема сосуда.

Устройство содержит крышку 1, герметично подсоединяемую к измеряемому сосуду 2, объем V₀ которого необходимо определить. Крышка 1 имеет толщину, позволяющую выполнить в ней отверстие 3, сообщающее внутреннюю часть крышки с наружной, и установить в нем уплотнительное кольцо 4, делящее его на две части. Стержень 5 установлен в отверстии 3 с возможностью его вращения в резьбовом соединении, выполненном в верхней части отверстия 3, и возвратно-поступательного перемещения его цилиндрической части в нижней части отверстия 3. Поворот стержня 5 осуществляется с помощью устройства поворота 6. Для определения угла поворота используются маркеры 7 и 8, установленные на стержне 5 и крышке 1. Вворачивая или выворачивая стержень 5 в крышку 1, изменяют величину искомого объема V₀ на значения ΔV₁, ΔV₂, ΔV, определяемые углом поворота и диаметром нижней части стержня 5. Для измерения давлений с помощью дифференциального датчика 12, создаваемых при перемещении стержня 5, в крышке 1 предусмотрены первый и второй каналы 9 и 10. Входы каналов 9 и 10 расположены на внутренней стороне крышки 1, при этом выход канала 9 перекрыт запорным клапаном 11, установленным на крышке 1. К выходу канала 10 подсоединен первый вход дифференциального датчика давления 12. Второй вход датчика 12 сообщается с атмосферой. Выходы датчика давления 12 и устройства поворота 6 подключены к устройству вычисления объема 13.

Описание узлов разработанного устройства измерения объема.

Измеряемым сосудом 2 может быть любой объект, имеющий внутреннюю полость и горлышко для доступа внутрь него. Для удержания крышки 1 на сосуде 2 используются зажимы или механизмы, например, типа резьбового соединения, используемого при ее повседневной эксплуатации, обеспечивающие герметичное соединение. Если необходимо измерить объем V_m твердого тела сложной формы, то оно помещается в сосуд с известным значением объема V_u, и, с помощью предлагаемого устройства, определяется незанятый им объем V₀=V_u-V_m, зная который вычисляется и искомый объем V_m.

Крышка 1 изготавливается из металла, например — дюралюминия, значительной толщины. Это позволяет с одной стороны избежать ее прогиба при надевании на сосуд и, следовательно, не изменять его объем при закрывании крышкой, а с другой — закрепить на ней все необходимые узлы (устройство поворота 6, датчик давления 12, запорный клапан 11, выполнить каналы 9 и 11 и, в зависимости от размеров крышки, установить даже устройство вычисления объема 13). В качестве крышки 1 для разработанного устройства может быть использован составной вариант, состоящий из обычной, стандартной крышки для конкретного сосуда с устройствами его крепления к нему, и герметично и жестко прикрепленной к ней толстой насадки, на которой и крепятся все узлы устройства. Обычная крышка имеет малую толщину, не позволяющую герметично и жестко закрепить на ней все используемые узлы, а насадка, являющаяся в данном случаем просто продолжением крышки, позволяет это сделать. Для временной герметизации плоскости крышки 1 с горлышком сосуда 2 используются густые смазки, например: циатим, литол или силиконовые герметики: Момент, автомобильные герметики-прокладки MaxSil, ABRO и другие. Крышка 1 имеет сквозное отверстие 3, причем, в верхней части отверстие имеет резьбу, в которую вворачивается стержень 5. Для уплотнения контакта крышки 1 с цилиндрической частью стержня 5 используется резиновое кольцо 4, вставленное в паз в месте окончания резьбы. Кольцо 4 должно герметично поджиматься и к стержню 5 и крышке 1, и не препятствовать вращению стержня 5. Оно имеет круглое сечение и выполнено из износостойкой резины. Нижняя часть отверстия 3 — цилиндрическая и имеет диаметр, обеспечивающий свободное вращение в нем нижней части стержня 5. Для дополнительной герметизации контакта целесообразно стержень 5 и отверстие 3 в крышке 2 смазать густым маслом типа циатим. Диаметр отверстия 3 в верхней и нижней частях крышки 1 может быть различным в зависимости от шага резьбового соединения и величин объемов ΔV₁, ΔV₂, ΔV, на которые будет изменяться объем исследуемого сосуда.

Стержень 5 изготавливается из металла, например — дюралюминия, при этом верхняя часть его имеет резьбу, а нижняя — гладкая, цилиндрическая. Нижняя часть стержня 5 должна плотно входить в крышку 1, обеспечивая герметичность сосуда 2 при его перемещении. Вворачивая или выворачивая стержень 5, изменяют объем сосуда 2 на величины ΔV₁, ΔV₂, ΔV. Для того, чтобы изначально не изменить объем сосуда, плоскости цилиндрической части стержня 5 и нижней части крышки 1 должны совпадать. Контроль совпадения осуществляется перед началом измерений давлений ΔP₁, ΔP₂ по положению маркеров 7 и 8, установленных на стержне 5 и крышке 1: когда плоскости совпадают, они должны находиться друг напротив друга. В этом случае, при повороте стержня на один оборот, величина изменяемого им объема V₁ легко определяется и равна V₁=πR²S, где R — радиус нижней части стержня 5, S — шаг резьбы. Изменяя число оборотов, изменяют и значение изменяемого объема. В частном случае, один из маркеров может представлять собой диск, размеченный на градусы, а второй — указатель в виде тонкой изогнутой проволоки или пластины с острым концом, расположенным над диском и позволяющим определять угол поворота. В этом случае величины изменяемых объемов ΔV₁, ΔV₂, ΔV могут быть выбраны произвольными из соображений максимальных значений уровней давлений, при которых надежно обеспечивается герметичность сосуда. Для упрощения реализации способа все же удобно изменять объем путем поворота стержня 5 на один или несколько оборотов. Использование винтового соединения существенно упрощает процедуру измерения вносимого объема, поскольку вследствие технологии его изготовления при повороте на 360 градусов объем будет изменяться всегда на одно и то же значение. Например, при уменьшении объема V₀ на величину ΔV давление при изменении объема на величину ΔV₂=ΔV₁ будет возрастать и очевидно, что ΔP₂ будет больше ΔP₁ и, следовательно, требования к герметичности сосуда возрастут, то чтобы их не увеличивать и не усложнять технологию измерения, целесообразно выбрать ΔV₂ меньшим чем ΔV₁. Например, для изменения объема на ΔV₁ стержень вворачивается на два оборота, а для изменения объема на ΔV₂ — только на один. В этом случае оба измерения будут проводиться при низких давлениях, что упрощает герметизацию закрытия сосуда. Изменение объема сосуда на величину ΔV может быть осуществлено различными способами. Например, как описано выше — путем вворачивания (или выворачивания) стержня в крышку на определенное число оборотов, соблюдая условие ΔV>ΔV₁, ΔV₂. В другом случае изменение объема на величину ΔV может быть осуществлено путем открытия крышки и помещения в сосуд объекта правильной формы, значение объема ΔV которого легко рассчитывается, например, куба или цилиндра из дюралюминия, с последующим закрытием крышки. Соблюдение указанного условия следует из анализа используемой формулы для расчета давления: при одной и той же точности измерения давлений, точность расчета объема будет тем выше, чем на большую величину будет изменен искомый объем V₀. Для получения погрешности измерения менее 1%, необходимо чтобы ΔV было больше 0,1 V₀.

Поворот стержня 5 в крышке 1 можно осуществить ручным или механизированным способом. При ручном способе поворот на заданный угол или число оборотов выполняется рукой. При механизированном способе для поворота используется шаговый двигатель, работающий под управлением микроконтроллера.

Для того, чтобы измерялись истинные дифференциальные давления ΔP₁, ΔP₂, перед изменением объема на величины ΔV₁, ΔV₂ необходимо выровнять давление внутри сосуда с окружающей средой. Для этих целей используется первый канал 9, имеющий диаметр порядка миллиметра. Объем канала должен быть малым в сравнении с исследуемым V₀, чтобы им можно было пренебречь, или его величину необходимо рассчитать и вычитать из измеренного значения объема.

Для перекрытия канала 9 на крышке размещают запорный клапан 11. Он может быть пружинного типа, поскольку создаваемые значения давлений имеют малые величины. При нажатии на клапан воздушная среда в сосуде соединяется с атмосферой (окружающей средой) и происходит выравнивание давлений, а при отпускании — выход канала 9 должен герметично закрываться. Силы поджатия исполняющего устройства клапана должно быть достаточным, чтобы не допустить разгерметизации при создаваемых уровнях давления ΔP₁, ΔP₂. Поскольку эти давления малы, то выполнить это условие не представляет труда. Для этих же целей можно использовать запорный электромагнитный клапан с нормально — закрытым каналом и ручным или электронным дистанционным управлением для случая автоматизации процесса измерения.

Для измерения давления используется дифференциальный датчик 12 давления, например фирмы Honeywell серий DUXL, ASDX (например, DUXL01D, ASDX005), фирмы On Semiconductor серии MPX (например, MPX2010D), один конец которого через канал 10 в крышке 1 соединен с внутренней полостью сосуда, а второй — с атмосферой. При выборе датчиков учитывается, что они должны работать при малых давлениях (менее 10 кПа) и, поэтому иметь максимальную чувствительность измерений. Выбор дифференциальной схемы измерений обусловлен ее высокой чувствительностью и точностью измерений. Созданные давления ΔP₁, ΔP₂ пропорциональны напряжениям U₁, U₂ на выходе датчика 12 с коэффициентом пропорциональности k (ΔP₁=kU₁, ΔР₂=kU₂). Поскольку в формуле для расчета объема (для случая, когда ΔV₁=ΔV₂) используется отношение давлений, то коэффициент k в числителе и знаменателе сокращается и вместо значений ΔP₁, ΔP₂ для расчета можно использовать соответствующие им значения напряжений U₁, U₂, что несколько упрощает вычисления.

Для подведения давления к датчику 12 используется второй канал 10 в крышке 1 устройства. Для уменьшения погрешности измерений его длина и объем должны быть минимизированы с тем, чтобы им можно было пренебречь или учесть. Поскольку этот объем постоянен, он подлежит вычитанию из общего измеряемого объема. Оба канала выполняют путем сверления отверстий в крышке, поэтому зная диаметр и измерив длину легко вычислить их объемы. Угол сверления значения не имеет.

После того, как в сосуде созданы давления ΔP₁, ΔP₂, необходимо убедиться, что сосуд герметично закрыт. Для этого наблюдают за показанием сигнала с выхода датчика 12 в течении нескольких секунд: если оно не изменяется — сосуд закрыт герметично и измеренное давление определено достоверно, если изменяется — значит сосуд закрыт негерметично, давление определяется с неконтролируемой ошибкой и расчет объема будет произведен неправильно. При обнаружении негерметичности сосуда, измерения проводить бессмысленно, необходимо найти место утечки воздуха и устранить ее причину. Важно, что в данном способе контроль герметичности осуществляется уже на первой стадии измерений (до изменения объема сосуда на величину ΔV) и при нарушении герметичности следующие стадии измерения уже не производятся, до устранения ее причины, что экономит общее время на проведение измерений.

Устройство 13 вычисления объема может быть выполнено различным образом. В простейшем случае, когда изменение объема осуществляется вручную, оно состоит из вольтметра, например, типа В7-22А, MAS830, позволяющего измерить напряжение на выходе датчика 12 и любого электронного калькулятора, например, CITIZEN SDC-888. В этом случае, последовательно измеряются напряжения, пропорциональные давлениям ΔP₁, ΔP₂, и с помощью калькулятора, зная значения ΔV₁, ΔV₂, ΔV по указанной в изобретении формуле рассчитывается искомый объем. В более сложном случае, устройство 13 может представлять собой электронный блок, состоящий из микроконтроллера (или компьютера) и аналого-цифровым преобразователем и индикатором результата расчета. Такой вариант целесообразен при автоматизации процесса измерения объема. Под управлением микроконтроллера осуществляются все операции по изменению указанных объемов, измерению и выравниванию давлений, и проведения расчета объема по предлагаемой в изобретении формуле. В этом случае, управление работой запорного клапана 11 так же осуществляется микроконтроллером.

Получить высокую чувствительность измерений можно путем изначального уменьшения исследуемого объема V на известную величину ΔV’ и измерении разности объемов V₀=V-ΔV’. Например, при измерении объема камер сгорания головки блока цилиндров двигателя, имеющих значительную открытую площадь для доступа и сложный профиль, внутренняя часть крышки может повторять контуры камеры с зазором в несколько миллиметров, исходя при этом из простоты ее закрывания, что в разы уменьшит измеряемый объем. При этом дополнительно вносимый ей объем ΔV’ определяется в результате калибровочных измерений и не изменяется. Так при объеме камеры 55 см³, которая по требованию должна иметь допуск не более +0,5÷-1,5 см³ необходимую точность измерений легко получить, уменьшив этот объем в 5 раз, выбрав ΔV’=44 см³, и измерять изменение объема ΔV₀=V₀-ΔV’=11 см³ для того же поля допусков, что, конечно, при прочих равных условиях, можно сделать более точно, чем измерение объема равного 55 см³. Это еще и упрощает способ измерения, поскольку уменьшение измеряемого объема приводит и к уменьшению значений изменяемых объемов ΔV, ΔV₁, ΔV₂, что технически осуществить более просто. Если сосуд имеет небольшую глубину и введение в него стержня технически сложно, то изменение объема сосуда на значения ΔV, ΔV₁, ΔV₂ можно осуществить путем его увеличения, то есть выворачивания стержня 5 из крышки 2, что говорит о расширении области применения предложенного способа измерения на сосуды самой различной формы, глубины и объема и является дополнительным достоинством способа.

В примере конкретной реализации устройства в качестве крышки 1 использовался диск из дюралюминия диаметром 45 мм и высотой 45 мм с прикрепленной к нему стандартной крышкой для сосуда. Крышка крепилась к горлышку сосуда 2 путем ее поворота на фиксированный угол. Для герметизации контакта крышки с ребром горлышка сосуда использовалась смазка — циатим. В крышку 1 вворачивался стержень 5 диаметром 27 мм и длиной 55 мм, имеющий в верхней части резьбу с шагом 1,5 мм. Нижняя часть стержня имела диаметр 23 мм и использовалась для изменения объема. Объем, изменяемый за один оборот стержня, равен 0,623 см³. Для обеспечения герметичности между крышкой 1 и стержнем 5 использовалось круглое в сечении резиновое кольцо 4, имеющее внутренний диаметр 22,5 мм, а внешний — 28 мм. Расстояние от кольца 4 до внутренней поверхности крышки равно 15 мм. На стержне 5 и крышке 1 изготовлено два маркера 7 и 8 из дюралюминия толщиной 1 мм: один (на стержне) в виде треугольника, а другой — в виде вертикально установленной пластины, ориентированных таким образом, что их плоскости совпадали при условии, что совпадали и плоскости торца стержня 5 и внутренней части крышки 1. В качестве дифференциального датчика давления 12 использовался датчик ASDX005D фирмы Honeywell в стандартной схеме включения с компенсацией постоянного напряжения 0,5 В на его выходе, для чего использовался операционный усилитель типа ОР-07 с коэффициентом усиления 6,46 в режиме работы сумматора исходного напряжения и напряжения -0,5 В. Установка такого коэффициента пропорциональности позволила получить на выходе напряжение, пропорциональное шкале мм. рт.ст. (10 миллиметров ртутного столба равно 1 вольту), хотя для расчета это не принципиально. Первый канал 9 имел длину 12 мм и диаметр 0,7 мм. Клапан 11 — оригинальный, пружинного типа, перекрывал выход канала 9, с помощью мягкой резины, поджимаемой пружиной через рычаг. При нажатии рукой на клапан 11 канал 9 открывался и давление в сосуде уравнивалось с атмосферным. Второй канал 10 имел диаметр 3 мм и длину 25 мм. Первый вход датчика 12 сообщался с внутренним объемом сосуда 2 через канал 10, а второй — с атмосферой. В качестве устройства вычисления объема 13 использовался вольтметр В7-22А и калькулятор CITIZEN SDC-888.

В первом частном случае реализации способа он работает следующим образом (см. фиг.1). Исследуемый сосуд 2 герметично закрывается крышкой 1. Выравнивается давление внутри него с окружающей средой путем нажатия на клапан 11. Вращением стержня 5 на два оборота уменьшают (или увеличивают) объем сосуда на величину ΔV₁. По отсутствию изменения показания напряжения на выходе датчика 12 в течение нескольких секунд, убеждаются, что сосуд закрыт герметично. Измеряют давление ΔP₁ на выходе датчика 12. Нажимают клапан 11 и выравнивают давление в сосуде 2 с атмосферой. Удерживая клапан 11, уменьшают (или увеличивают) объем сосуда 2 на величину ΔV путем вворачивания (выворачивания) в крышку стержня 5 и отпускают клапан 11. Вращением стержня 5 уменьшают (или увеличивают) объем сосуда 2 на величину ΔV₂. По изменению напряжения на выходе датчика 12 повторно убеждаются в герметичности сосуда. Определяют значение давления ΔP₂, и производят расчет объема сосуда по формуле: V₀=(ΔV·k·ΔP₂/ΔV₂)/(ΔP₂/ΔV₂-ΔP₁/ΔV₁), где: k=7, если объем сосуда уменьшают и k=-1, если увеличивают.

Например, требуется определить объем стеклянного сосуда сложной формы (фигурная банка), который составляет 23,5 см³. Измеряемый сосуд 2 герметично накрывают крышкой 1 с размещенными на ней узлами измерения. Нажатием на клапан 11 выравнивают давление в сосуде 2 с атмосферой. Вворачивают стержень 5 в крышку 1 на два оборота (ΔV₁=1,25 см³) и измеряют созданное этим давление ΔP₁=31,4 мм. рт.ст. По отсутствию изменения показания давления на выходе датчика 12 убеждаются в герметичности закрытия сосуда 2. Нажимают на клапан 11 и вворачивают стержень 5 еще на два оборота. В результате общее изменение объема за четыре оборота равно ΔV=2,49 см³ (11% от измеряемого объема). Клапан 11 отпускают и вворачивают стержень еще на два оборота, после чего измеряют созданное давление ΔP₂=35,1 мм. рт.ст. Убеждаются, что оно не изменяется в течение нескольких секунд, что подтверждает герметичность закрытия сосуда. С помощью калькулятора рассчитывают искомый объем по формуле: V₀=ΔV/(1-ΔP₁/ΔP₂). Рассчитанное значение V₀=23,6 см³, относительная погрешность измерения — 0,4%.

Во втором частном случае реализации способа при измерении значительных объемов для увеличения точности измерений объем сосуда V изначально уменьшают на величину ΔV’ и измеряют разницу V₀=V-ΔV’, определив которую рассчитывают истинное значением объема сосуда. Например, объем сосуда, который нужно измерить составляет V=167 см³. Для его уменьшения помещают в него цилиндр из дюралюминия объемом ΔV’=137 см³, измеренный с погрешностью 0,1%. По приведенной выше методике определяем объем V₀=6,48/(1-24,7/31,5)=30,02 см³ (погрешность измерения истинного значения V₀ равного 30 см³ составляет 0,07%). Вычисленное значение объема V=ΔV’+V₀=167,02 см³, а погрешность его определения равна 0,01%, т.е. ниже, чем погрешность определения V₀.

1. Способ измерения объема сосуда, заключающийся в том, что изменяют объем сосуда на величину ΔV и определяют изменение давления газа в сосуде до и после изменения объема, на основании которых определяют искомый объем сосуда V₀, отличающийся тем, что предварительно выравнивают давление в герметично закрытом сосуде с окружающей средой, перемещением стержня изменяют его объем на величину ΔV₁ и измеряют давление ΔP₁ внутри сосуда по отношению к внешней среде, убеждаются, что оно не изменяется с течением времени, изменяют объем сосуда на величину ΔV, выравнивают давление в сосуде с окружающей средой, повторно изменяют объем сосуда на величину ΔV₂, измеряют давление ΔР₂ внутри сосуда по отношению к внешней среде и повторно убеждаются, что оно не изменяется с течением времени, а искомый объем сосуда V₀ определяют по формуле: V₀=(ΔV·k·ΔP₂/ΔV₂)/(ΔP₂/ΔV₂-ΔP₁/ΔV₁), где k=1, если объем сосуда уменьшают, и k=-1, если увеличивают.

2. Способ измерения объема сосуда по п.1, отличающийся тем, что перед проведением измерений объем измеряемого сосуда уменьшают на известную величину, а истинный объем определяют как сумму измеренного и введенного в сосуд объемов.

3. Устройство для измерения объема сосуда, содержащее крышку, герметично подсоединенную к сосуду, и устройство для расчета объема сосуда по формуле, отличающееся тем, что крышка выполнена толстостенной и содержит отверстие, в котором установлено уплотнительное кольцо, делящее его на верхнюю и нижнюю части, при этом верхняя часть отверстия имеет резьбу, а цилиндрический стержень, установленный в отверстии и соединенный с крышкой посредством резьбового соединения, выполнен с возможностью его вращения и осевого перемещения его цилиндрической части в нижней части отверстия, причем на крышке закреплено устройство поворота упомянутого стержня на заданный угол, а в крышке выполнены первый и второй сквозные каналы, входы которых расположены на внутренней стороне крышки, на крышке установлен запорный клапан, перекрывающий соединение первого канала с атмосферой, при этом к выходу второго канала подключен первый вход дифференциального датчика давления, второй его вход сообщается с атмосферой, а его выход и выход устройства поворота соединены с устройством расчета объема.

нюансы расчета объема жидкости в зависимости от формы емкости

Что такое вместимость сосуда

Вместимость сосуда — это объем его внутренней полости, определяемый по его геометрическим параметрам. Единица измерения объема в СИ — кубический метр, но в случае жидкости чаще используют литр.

Особенности расчета объема жидкости в сосуде

Жидкость по своим свойствам занимает промежуточное место между двумя другими агрегатными состояниями вещества — твердым и газообразным. Жидкости присущи некоторые свойства и твердого тела, и газа. Силы взаимного притяжения молекул в жидкостях достаточно велики, чтобы удерживать молекулы вместе, так что, в отличие от газов, жидкости имеют постоянный собственный объем.

В то же время эти силы недостаточны, чтобы держать молекулы в жесткой упорядоченной структуре, и потому у жидкостей нет постоянной формы: они принимают форму сосуда, в котором находятся.

Осторожно! Если преподаватель обнаружит плагиат в работе, не избежать крупных проблем (вплоть до отчисления). Если нет возможности написать самому, закажите тут.

Жидкость в сосуде оказывает постоянное давление на его стенки, поэтому на производстве, где необходимо регулярно измерять текущий объем жидкости в сосуде, часто используют гидростатические датчики давления.

За счет маленького диаметра их мембран итоговая погрешность измерения близится к нулю. Поэтому, зная давление в конкретный момент времени, можно вычислять уровень жидкости, т. е. высоту гидростатического столба. В формулу для расчета входят только плотность жидкости и ее давление:

\(h = \frac{p}{\rho \times g}.\)

\(p\) здесь — давление в паскалях, \(\rho\) — плотность, \(g\) — ускорение свободного падения, константа.

Зная габариты сосуда, несложно рассчитать объем жидкости в нем. Это необходимо, например, в пивоварении и виноделии, где обычно используются цилиндрические емкости с конусным дном, близкие по параметрам к идеальным геометрическим телам.{3}}{3}.\)

Современные способы измерения объема жидкости

Одной из важнейших задач молочной промышленности всегда был учет объема продукта: поступившего на обработку, расходуемого в течение технологического процесса, полученного на выходе. Причем эти измерения требуются как для технологических задач, так и для экономического учета.

О современных способах произведения этих измерений и пойдет речь.Существует несколько подходов к измерению объема жидкости, находящейся в емкости. Все они, однако, имеют одну общую исходную величину, требуемую для расчета. Эта величина – высота столба жидкости.Известна формула, устанавливающая математическую связь между плотностью жидкости, высотой ее столба относительно точки измерения, ускорением свободного падения и давлением, оказываемым на дно и стенки сосуда:

P=ρ×g×hP= %rho times g times h

где Р – давление, ρ – плотность жидкости, h – высота столба жидкости, g – ускорение свободного падения (9,8 м/c²).

Итак, зная давление и плотность жидкости, нетрудно рассчитать высоту, до которой она доходит относительно точки измерения. Такой способ измерения называется гидростатическим.Для того, чтобы узнать давление жидкости используются соответствующие датчики. В пищевой промышленности, как правило, это датчики с мембраной, имеющие относительно большую плоскость контакта со средой, что позволяет легко отмывать их от остатков продукта.

Среди датчиков давления наиболее распространены датчики с выходным сигналом 4…20 мА, являющимся общемировым стандартом в системах автоматического управления. Например, интеллектуальный датчик давления 4000-SAN.Сам чувствительный элемент датчика обычно представляет собой тензорезистор – элемент, изменяющий свое сопротивление в зависимости от приложенного к нему усилия. Зависимость сопротивления этих элементов от давления известна. Далее изменение сопротивления электроника датчика приводит к сигналу 4…20 мА.Современные датчики давления часто делаются цифровыми – то есть роль преобразователя играет микроконтроллер, встроенный в датчик. Такие датчики легче настраивать, они обладают более высокой точностью и могут оснащаться дисплеями, модулями коммуникации и дополнительными функциональными возможностями.

Итак, после того, как получено значение высоты, можно переходить к расчету объема жидкости. Выделяются два основных практических подхода:

• геометрическое вычисление;
• аппроксимация линейными отрезками.
  

1. Первый способ измерения объема жидкости: вычисление высоты

Рисунок 1 — Цилиндрическая емкость с коническим дном

Первый способ подразумевает возможность выражения зависимости высота – объем известной формулой. Он актуален для емкостей, имеющих несложную форму и построенных из таких стандартных геометрических фигур, как, например, полусфера, конус и цилиндр. Например, для широко распространенных емкостей в форме цилиндра с коническим дном (Рисунок 2), вычисление будет производиться следующим образом: до тех пор, пока жидкость не достигла края конуса зависимость ее объема от высоты такова:

V=13×π×Hж×((R2+K×H)2+(R2+K×H)×R2+R22)V= {1} over {3} times %pi times Hж times ( ( R_{2} + K times H )^{2} + ( R_{2} + K times H ) times R _{2} + R_{2} ^{2})

Где V – объем, Нж – высота столба жидкости, K – конусность

K=R1−R2h2K= { R_{1} — R_{2} } over {H_{1}}

как только высота жидкости достигает края конуса и начинает заполнять цилиндр достаточно взять заранее вычисленный полный объем конической части:

Vk=13×π×h2×(R12+R1×R2+R22) Vk= {1} over {3} times %pi times H_{1} times ( R^{2}_{1} + R_{1} times R_{2} + R^{2}_{2} )

и прибавлять к нему объем жидкости, находящейся в цилиндрической части:

Vц=π×R12×(Нж−h2)Vц= %pi times R_{1}^{2} times ( Нж — H_{1} )

С учетом степени развития микроконтроллеров, подобный алгоритм возможно реализовать непосредственно в датчике.{3}

или 47,1 литров.

Достаточно большое значение, с учетом того, что в течение рабочего дня могут производиться десятки циклов наполнения/опустошения емкости. При этом данное значение не учитывает дополнительную погрешность, вызываемую перепадами температуры.Именно поэтому датчики для решения задач вычисления объема обычно имеют погрешность не более 0,1 %. При тех же условиях, такой датчик даст ошибку измерения всего в 9,42 литра, то есть в 5 раз меньшую.

3. Второй способ вычисления: аппроксимация

Рисунок 2 — Емкость под углом

На практике часто встречаются емкости, имеющие искажения формы внутренней поверхности, к которым неприменим геометрический метод вычисления объема емкости.Например, для емкости, установленной под углом (Рисунок 2), наклон в 2…3 градуса, кажущийся незначительным, сильно нарушит точность измерений – в горизонтальной емкости поверхность жидкости вместо прямоугольника будет иметь гораздо более сложную форму, что значительно меняет зависимость объема от уровня.

Емкость может иметь утопленный в стенку люк. В этом случае нужно производить вычисления уже по трем разным формулам, вместо двух. К тому же, зависимость объема на участке с люком будет куда более сложной, чем для прямого цилиндра. Также, геометрический метод на практике неприменим к емкостям, в которых производится перемешивание продукта.

Массивное устройство внутри емкости значительно исказит результаты вычислений – датчик будет показывать объем, больший, чем реальный. Предусмотреть готовые алгоритмы для каждой подобной ситуации и внести их в датчик – задача практически невыполнимая. Тут на помощь приходит более трудоемкий, но и значительно более гибкий способ измерения. Если начать заливать в емкость, допустим, по 100 литров жидкости и при этом на каждом шаге отмечать высоту, соответствующую залитому объему, мы получим так называемую «тарировочную таблицу». Суть в следующем: нестандартная форма емкости моделируется с использованием некоторого количества прямых отрезков. Чем их больше, тем точнее будут производиться вычисления. Таким образом, можно высоте столба жидкости поставить в соответствие ее объем.

Рисунок 3 — Реальная и аппроксимированная зависимости объема жидкости от высоты

Если жидкость, например, находится посередине между двумя точками, то и объем вычисляется, как среднее значение объемов в этих точках (Рисунок 3). Очевидно, что от количества точек, используемых при тарировании, значительно зависит точность результата. Если для участка с линейной зависимостью объем/высота достаточно двух точек, до для нелинейных участков их требуется гораздо больше. Тарирование на нелинейном участке можно производить шагами, в два раза большими, чем допустимая погрешность на данном участке. Например, если в конусной части емкости необходимо получить точность не ниже 20 литров, шаги тарирования должны быть не более 40 литров. Тут следует помнить простое правило – чем меньше шаги и больше точек, тем выше итоговая точность работы. Недостаток метода в том, что датчик, перенесенный на другую емкость, снова потребует тарирования. Однако, единожды оттарированный на одной емкости датчик будет не только давать максимально высокую точность вычислений, но и позволит подсчитывать объем для жидкостей с различными плотностями – достаточно будет лишь ввести в него это значение.

Это значит, что можно произвести тарирование с использованием обычной воды, а затем, предварительно поменяв значение плотности жидкости в памяти датчика, заливать продукт, имеющий плотность, отличную от плотности воды. Таким образом, мы получаем гибкий и точный метод, позволяющий работать с емкостями любой формы и жидкостями любой плотности.

Инженер отдела проектирования ООО «КИП-Сервис»
Горбоносов М.А.

Читайте также:

Глава 13. Газовые законы

Задачи на газовые законы часто предлагаются школьникам на едином государственном экзамене. Для решения этих задач вполне достаточно знать уравнение состояния идеального газа (закон Клапейрона-Менделеева) и уметь использовать его алгебраически и геометрически (для построения графиков зависимости одних параметров газа от других) в простейших ситуациях. Кроме того, нужно понимать, как описываются смеси идеальных газов (закон Дальтона).

Уравнение, связывающее параметры газа друг с другом, называется уравнением состояния. Для идеального газа, взаимодействие молекул которого мало, уравнение состояния имеет вид

(13.1)

где — давление газа, — концентрация молекул газа (число молекул в единице объема), — постоянная Больцмана, — абсолютная (в шкале Кельвина) температура. Учитывая, что , где — число молекул газа, — объем сосуда, в котором находится газ (часто говорят объем газа), получим из (13.1)

(13.2)

Число молекул можно связать с количеством вещества газа : , где — число Авогадро. Поэтому формулу (13.2) можно переписать в виде

(13.2)

где произведение постоянных Авогадро и Больцмана обозначено как . Постоянная = 8,31 Дж/(К•моль) называется универсальной газовой постоянной. Количество вещества газа можно также выразить через его массу и молярную массу этого газа

(13.3)

С учетом (13.3) закон (13.2) можно переписать и в таком виде

(13.4)

Уравнение состояния идеального газа (13.1)-(13.4), которое также называется уравнением (или законом) Клапейрона-Менделеева, позволяет связывать параметры идеального газа и проследить за их изменением в тех или иных процессах.

В школьном курсе физики рассматриваются три изопроцесса, в которых один из трех параметров газа (давление, температура и объем) не изменяется. В изобарическом процессе не изменяется давление газа, в изотермическом — температура, в изохорическом — объем. Изопроцессам отвечают следующие графики зависимости давления от объема, давления от температуры, объема от температуры.

Для изобарического процесса

Первые два графика очевидны. Последний получается так. Из закона Клапейрона-Менделеева следует, что зависимость объема от температуры при постоянном давлении имеет вид

(13.5)

где — постоянная. Графиком функции (13.5) является прямая, продолжение которой проходит через начало координат.

Для изохорического процесса

Второй график следует из соотношения

(13.6)

где — постоянная при постоянном объеме.

Для изотермического процесса

Первый график следует из закона Клапейрона-Менделеева, который при постоянной температуре газа можно привести к виду

(13.7)

где — постоянная. Отсюда следует, что графиком зависимости от в изотермическом процессе является гипербола.

Важнейшее свойство уравнения состояния идеального газа (13.1)-(13.4) заключается в том, что «индивидуальность» газа никак не проявляется в этих законах — единственный параметр собственно газа, входящий в уравнение состояния, — это число молекул. Например, 1 моль гелия и 1 моль азота, находящиеся в одинаковых объемах и имеющие одинаковые температуры, оказывают одинаковое давление. Отсюда следует, что и давление смеси идеальных газов определяется суммарным числом молекул всех компонент смеси:

(13.8)

где — число молекул первой, второй, третьей и т.д. компонент смеси, — постоянная Больцмана, — абсолютная температура смеси, — объем сосуда. Величины , имеющие смысл давления каждой компоненты смеси при условии, что она имела бы такую же температуру и занимала бы весь объем, называются парциальными давлениями компонент. Закон (13.8) называется законом Дальтона. Рассмотрим теперь в рамках этих законов предложенные выше задачи.

В задаче 13.1.1 из уравнения состояния в форме (13.1), получаем для давления в конце процесса :

т.е. давление газа увеличилось в 6 раз (ответ 1).

Применяя закон Клапейрона-Менделеева (13.2) к первому и второму газам (задача 13.1.2), получаем

где — искомый объем. Сравнивая первую и вторую формулы, заключаем, что (ответ 1).

Закон Клапейрона-Менделеева для газа в начальном и конечном состояниях (задача 13.1.3) дает

где — неизвестная температура. Из сравнения этих формул получаем , т.е. температуру газа в сосуде нужно повысить вдвое (ответ 2).

Из закона Клапейрона-Менделеева для начального и конечного состояний газа в задаче 13.1.4 имеем

Отсюда , т.е. количество вещества газа в сосуде увеличилось в 1,25 раза (ответ 3).

Первым, кто понял, почему жидкость поднимается вместе с трубкой (задача 13.1.5), и почему «природа боится пустоты» (Аристотель), но только до определенного предела, был знаменитый итальянский физик, современник Г. Галилея Э. Торричелли. Давайте рассмотрим рассуждения Торричелли подробно. Основная идея Торричелли заключалась в том, что атмосферный воздух оказывает давление на все поверхности, с которыми он контактирует. В равновесии жидкость занимает такое положение, чтобы все воздействия на каждый ее элемент компенсировались. Если бы трубка была открыта (см. левый рисунок), то жидкость не поднялась бы в трубке. Действительно, в этом случае на бесконечно малый элемент жидкости в трубке около поверхности (выделен на рисунке) действовали бы сила со стороны атмосферного воздуха в трубке, направленная вниз. С другой стороны, атмосферный воздух действует и на остальную поверхность жидкости, и это воздействие благодаря закону Паскаля передается выделенному элементу жидкости в трубке снизу. Таким образом, воздействие воздуха на поверхность жидкости в трубке и на свободную поверхность жидкости компенсируют друг друга, если уровень жидкости в трубке совпадает с уровнем жидкости в остальном сосуде. Если же мы поднимаем трубку, выпустив из нее воздух, на рассматриваемый элемент жидкости воздух сверху не действует (его нет в трубке), поэтому воздействие воздуха на свободную поверхность жидкости приведет к тому, что жидкость войдет в трубку и заполнит ее. При вытаскивании трубки жидкость будет подниматься вслед за ней. Однако при дальнейшем поднятии трубки наступит такой момент, когда воздействие воздуха на свободную поверхность и столба жидкости в трубке сравняются (в этот момент атмосферное давление будет равно гидростатическому давлению жидкости в трубке на уровне свободной поверхности). Дальнейший подъем трубки уже не приведет к поднятию жидкости — атмосферное давление не сможет «держать» столб жидкости большей высоты. Для воды этот столб составляет около 10 м, для ртути, с которой и экспериментировал Э. Торричелли, — 76 сантиметров. Таким образом, жидкость в трубке поднимается благодаря давлению атмосферного воздуха на поверхность воды в сосуде и закону Паскаля (ответ 4).

Сравнивая графики процессов 1, 2, 3 и 4, данные в условии задачи 13.1.6, с графиками изопроцессов, приведенными во введении к настоящей главе, заключаем, что: процесс 1 — изотермический, 2 — изохорический, 3 — изобарический. В процесс 4 меняются и давление, и объем, и температура газа (ответ 4).

В изотермическом процессе давление зависит от объема как ; на диаграмме этот процесс изображается гиперболой. Поэтому изотермическими являются процессы 1 и 3 (задача 13.1.7), но в процессе 1 объем газа убывает. Следовательно, изотермическим расширением является процесс 3 (ответ 3).

Изохорическим охлаждением в задаче 13.1.8 является процесс 4 (см. рисунок) В двух последних задачах этого варианта нужно с помощью закона Клапейрона-Менделеева вычислить один из параметров газа, если даны остальные параметры. В задаче 13.1.9 из закона Клапейрона-Менделеева

получим

(ответ 1).

В задаче 13.1.10 при вычислениях следует не забыть перевести температуру газа в Кельвины. Из закона Клапейрона-Менделеева находим

(ответ 1).

Из уравнения состояния в форме (13.2) следует, что при одинаковых объемах и температурах давление идеального газа определяется только полным числом молекул. Поэтому отношение давления водорода и гелия в задаче 13.2.1 равно 2 (ответ 2).

Поскольку перегородка в задаче 13.2.2 подвижная и находится в равновесии, давления газа в отсеках сосуда слева и справа от перегородки равны. Применяя к ним при этом условии закон Клапейрона-Менделеева, получим

для гелия

для азота

где температуры и массы газов по условию одинаковы. Деля эти уравнения друг на друга, находим отношение объемов частей сосуда

(ответ 4).

Если бы точки, отвечающие состояниям 1 и 2 в задаче 13.2.3, лежали на одной прямой, продолжение которой проходит через начало координат, то эти состояния принадлежали бы одной и той же изохоре, и, следовательно, объем газа в этих состояниях был одинаковым (см. формулу (13.6)). Поэтому для сравнения объемов этих состояний построим изохоры, проходящие через точки 1 и 2, и сравним отвечающие им объемы (см. рисунок; изохоры, проходящие через точки 1 и 2, показаны пунктиром).

Из формулы (13.6) следует, что чем больше объем, тем меньше коэффициент перед в зависимости (13.6), и, следовательно, меньше наклон соответствующей изохоры к оси температур. Поэтому изохоре 1 отвечает больший объем, чем изохоре 2, и, следовательно, объем газа в процессе 1-2 уменьшается (ответ 2).

Аналогичные рассуждения в задаче 13.2.4 показывают, что наибольшему давлению отвечает изобара, проходящая через точку (поскольку соответствующая прямая имеет наименьший наклон к оси температур; см. рисунок ниже). Поэтому правильный ответ в этой задаче — 3.

В закон Клапейрона-Менделеева входит абсолютная температура газа, поэтому данные в задаче 13.2.5 значения нужно перевести в Кельвины. В результате для отношения давлений газа в конечном и начальном состояниях получаем

(ответ 4).

Как следует из опыта, при приведении тел в тепловой контакт выравниваются их температуры. Это же касается и частей одного тела или даже компонент смеси газов (задача 13.2.6). Поэтому температуры компонент смеси будут одинаковы (ответ 1). Что касается парциальных давлений, плотностей или концентрации компонент смеси, то их значения зависят от количества молекул каждой компоненты смеси и могут быть различны.

Парциальное давление компонент смеси – это давление, которое оказывают только молекулы каждой компоненты. Как следует из формулы (13.8) парциальное давление любой компоненты можно найти, применяя только к ней закон Клапейрона-Менделеева и считая, что она имеет такую же температуру, как и вся смесь, и занимает такай же объем, как и вся смесь газов. Поэтому отношение парциальных давлений отдельных компонент смеси равно отношению количеств вещества (или числа молекул) этих компонент. Поэтому для отношения парциальных давлений углекислого газа и гелия в сосуде в задаче 13.2.7 имеем (ответ 2).

Как следует из закона Дальтона, давление смеси газов определяется полным количеством молекул в ней. Поэтому для анализа изменения давления смеси газов при протекании в ней химической реакции (задача 13.2.8) необходимо исследовать изменение числа молекул. Гелий не участвует в химической реакции — один моль гелия был и в начальном, и в конечном состоянии смеси. С озоном происходила реакция

т.е. из двух молекул озона в результате реакции получились три молекулы кислорода. Поэтому два моля озона превратились в три моля кислорода, и общее количество вещества смеси стало равно четырем молям. Поэтому давление смеси увеличивается в 4/3 раза (ответ 2).

Поскольку объемы и температуры газов одинаковы (задача 13.2.9), для сравнения их давлений необходимо сравнить число молекул в них. По условию в одном сосуде находится один моль азота, в другом 1 г водорода (т.е. половина моля) и 3 • 10²³ молекул гелия (тоже половина моля). Поэтому и в одном и в другом сосуде находятся одинаковые количества молекул, и, следовательно, давление газов в них одинаково (ответ 3).

Плотность газа (задача 13.2.10) можно найти из следующей цепочки формул

(ответ 4). Здесь — масса газа, — масса одной молекулы газа.

100 ballov.kz образовательный портал для подготовки к ЕНТ и КТА

Код и классификация направлений подготовки	Код группы образовательной программы	Наименование групп образовательных программ	Количество мест
8D01 Педагогические науки
8D011 Педагогика и психология	D001	Педагогика и психология	45
8D012 Педагогика дошкольного воспитания и обучения	D002	Дошкольное обучение и воспитание	5
8D013 Подготовка педагогов без предметной специализации	D003	Подготовка педагогов без предметной специализации	22
8D014 Подготовка педагогов с предметной специализацией общего развития	D005	Подготовка педагогов физической культуры	7
8D015 Подготовка педагогов по естественнонаучным предметам	D010	Подготовка педагогов математики	30
	D011	Подготовка педагогов физики (казахский, русский, английский языки)	23
	D012	Подготовка педагогов информатики (казахский, русский, английский языки)	35
	D013	Подготовка педагогов химии (казахский, русский, английский языки)	22
	D014	Подготовка педагогов биологии (казахский, русский, английский языки)	18
	D015	Подготовка педагогов географии	18
8D016 Подготовка педагогов по гуманитарным предметам	D016	Подготовка педагогов истории	17
8D017 Подготовка педагогов по языкам и литературе	D017	Подготовка педагогов казахского языка и литературы	37
	D018	Подготовка педагогов русского языка и литературы	24
	D019	Подготовка педагогов иностранного языка	37
8D018 Подготовка специалистов по социальной педагогике и самопознанию	D020	Подготовка кадров по социальной педагогике и самопознанию	10
8D019 Cпециальная педагогика	D021	Cпециальная педагогика	20
		Всего	370
8D02 Искусство и гуманитарные науки
8D022 Гуманитарные науки	D050	Философия и этика	20
	D051	Религия и теология	11
	D052	Исламоведение	6
	D053	История и археология	33
	D054	Тюркология	7
	D055	Востоковедение	10
8D023 Языки и литература	D056	Переводческое дело, синхронный перевод	16
	D057	Лингвистика	15
	D058	Литература	26
	D059	Иностранная филология	19
	D060	Филология	42
		Всего	205
8D03 Социальные науки, журналистика и информация
8D031 Социальные науки	D061	Социология	20
	D062	Культурология	12
	D063	Политология и конфликтология	25
	D064	Международные отношения	13
	D065	Регионоведение	16
	D066	Психология	17
8D032 Журналистика и информация	D067	Журналистика и репортерское дело	12
	D069	Библиотечное дело, обработка информации и архивное дело	3
		Всего	118
8D04 Бизнес, управление и право
8D041 Бизнес и управление	D070	Экономика	39
	D071	Государственное и местное управление	28
	D072	Менеджмент и управление	12
	D073	Аудит и налогообложение	8
	D074	Финансы, банковское и страховое дело	21
	D075	Маркетинг и реклама	7
8D042 Право	D078	Право	30
		Всего	145
8D05 Естественные науки, математика и статистика
8D051 Биологические и смежные науки	D080	Биология	40
	D081	Генетика	4
	D082	Биотехнология	19
	D083	Геоботаника	10
8D052 Окружающая среда	D084	География	10
	D085	Гидрология	8
	D086	Метеорология	5
	D087	Технология охраны окружающей среды	15
	D088	Гидрогеология и инженерная геология	7
8D053 Физические и химические науки	D089	Химия	50
	D090	Физика	70
8D054 Математика и статистика	D092	Математика и статистика	50
	D093	Механика	4
		Всего	292
8D06 Информационно-коммуникационные технологии
8D061 Информационно-коммуникационные технологии	D094	Информационные технологии	80
8D062 Телекоммуникации	D096	Коммуникации и коммуникационные технологии	14
8D063 Информационная безопасность	D095	Информационная безопасность	26
		Всего	120
8D07 Инженерные, обрабатывающие и строительные отрасли
8D071 Инженерия и инженерное дело	D097	Химическая инженерия и процессы	46
	D098	Теплоэнергетика	22
	D099	Энергетика и электротехника	28
	D100	Автоматизация и управление	32
	D101	Материаловедение и технология новых материалов	10
	D102	Робототехника и мехатроника	13
	D103	Механика и металлообработка	35
	D104	Транспорт, транспортная техника и технологии	18
	D105	Авиационная техника и технологии	3
	D107	Космическая инженерия	6
	D108	Наноматериалы и нанотехнологии	21
	D109	Нефтяная и рудная геофизика	6
8D072 Производственные и обрабатывающие отрасли	D111	Производство продуктов питания	20
	D114	Текстиль: одежда, обувь и кожаные изделия	9
	D115	Нефтяная инженерия	15
	D116	Горная инженерия	19
	D117	Металлургическая инженерия	20
	D119	Технология фармацевтического производства	13
	D121	Геология	24
8D073 Архитектура и строительство	D122	Архитектура	15
	D123	Геодезия	16
	D124	Строительство	12
	D125	Производство строительных материалов, изделий и конструкций	13
	D128	Землеустройство	14
8D074 Водное хозяйство	D129	Гидротехническое строительство	5
8D075 Стандартизация, сертификация и метрология (по отраслям)	D130	Стандартизация, сертификация и метрология (по отраслям)	11
		Всего	446
8D08 Сельское хозяйство и биоресурсы
8D081 Агрономия	D131	Растениеводство	22
8D082 Животноводство	D132	Животноводство	12
8D083 Лесное хозяйство	D133	Лесное хозяйство	6
8D084 Рыбное хозяйство	D134	Рыбное хозяйство	4
8D087 Агроинженерия	D135	Энергообеспечение сельского хозяйства	5
	D136	Автотранспортные средства	3
8D086 Водные ресурсы и водопользование	D137	Водные ресурсы и водопользования	11
		Всего	63
8D09 Ветеринария
8D091 Ветеринария	D138	Ветеринария	21
		Всего	21
8D11 Услуги
8D111 Сфера обслуживания	D143	Туризм	11
8D112 Гигиена и охрана труда на производстве	D146	Санитарно-профилактические мероприятия	5
8D113 Транспортные услуги	D147	Транспортные услуги	5
	D148	Логистика (по отраслям)	4
8D114 Социальное обеспечение	D142	Социальная работа	10
		Всего	35
		Итого	1815
		АОО «Назарбаев Университет»	65
		Стипендиальная программа на обучение иностранных граждан, в том числе лиц казахской национальности, не являющихся гражданами Республики Казахстан	10
		Всего	1890

Объем и смачиваемая площадь частично заполненных горизонтальных сосудов

Расчет смачиваемой площади и объема горизонтальных сосудов требуется для инженерных задач, таких как исследования пожара и определение сигналов тревоги уровня и контрольных точек. Однако расчет этих параметров затруднен из-за геометрии судна, особенно из-за головок. В этой статье подробно описаны формулы для расчета площади смачивания и объема этих сосудов для различных типов изогнутых концов, включая полусферические, торисферические, полуэллипсоидальные и выпуклые.

над дном сосуда Общий объем

	:	Смачиваемая зона
	:	Внутренний диаметр сосуда
	:	Внешний диаметр сосуда
	:
	:
	:	Длина сосуда, от линии загара до линии загара
	:	Прямой фланец
	:	Радиус внутренней части сосуда
	:
	:	Внутренний радиус кулака
	:	Толщина стенки сосуда
	:	Объем частично заполненной жидкости
	:	головки или сосуда		:	Внутренняя глубина тарелки
	: 90 009	Эксцентриситет эллиптических головок

Расчет объема жидкости или смачиваемой площади частично заполненного горизонтального сосуда лучше всего выполнять по частям, вычисляя значение для цилиндрического сечения сосуда и днищ сосуда и затем сложите области или объемы вместе.Ниже мы представляем смачиваемую площадь и частично заполненный объем для каждого типа головки и цилиндрической секции.

Частично заполненный объем в основном используется для расчета времени наполнения резервуара и установки контрольных уставок, уровней срабатывания сигнализации и точек срабатывания системы.

Смоченная область — это область контакта жидкости со стенкой резервуара. Это в первую очередь используется при пожарных исследованиях технологических резервуаров и резервуаров для хранения, чтобы определить мощность аварийной вентиляции, необходимую для защиты резервуара.

Объем и смачиваемая площадь частично заполненных вертикальных сосудов рассматриваются отдельно.

Полусферические головки имеют глубину, равную половине их диаметра. Они имеют самое высокое расчетное давление из всех типов головок и, как таковые, обычно являются наиболее дорогими типами головок. Формула для расчета смачиваемой площади и объема одной головы представлена ​​следующим образом.

Смачиваемая область

Volume

Полуэллипсоидальные головки меньше полусферических головок и глубже торисферических головок, поэтому их расчетное давление и стоимость лежат между этими двумя конструкциями.

Наиболее распространенным вариантом полуэллипсоидальной головки является эллиптическая головка 2: 1, имеющая глубину, равную 1/4 диаметра сосуда. Формула для расчета смачиваемой площади и объема для одной полуэллиптической головки 2: 1 представлена ​​следующим образом.

Смачиваемая поверхность

Для полуэллипсоидального напора 2: 1 ε равно 0,866, для других геометрических форм можно использовать формулу ниже для расчета ε.

Площадь смачивания, рассчитанная с помощью этого метода, не включает прямой фланец головки.Длину прямого фланца необходимо учитывать при расчете смачиваемой площади цилиндрического сечения.

Объем

Где,

для ASME 2: 1 Эллиптические головки:

для DIN 28013 Полуэллиптические головки:

Рассчитанный объем не включает прямой фланец головки, только изогнутую часть. Длину прямого фланца необходимо учитывать при расчете объема цилиндрического сечения.

Торсферические головки являются наиболее экономичными и поэтому являются наиболее распространенным типом головок, используемых для технологических сосудов.Торсферические головки имеют меньшую глубину и обычно имеют более низкое расчетное давление, чем полуэллиптические головки. Формула для расчета смачиваемой площади и объема одной частично заполненной торсферической головки представлена ​​следующим образом.

Смачиваемая площадь

Мы можем аппроксимировать частично заполненную площадь поверхности торисферической головки, используя формулу для эллиптических головок. Это приближение приведет к завышению оценки площади поверхности, поскольку торсферическая головка более плоская, чем эллипсоидальная.Это предположение консервативно для расчетов пожаротушения бассейнов.

Площадь смачивания, рассчитанная с помощью этого метода, не включает прямой фланец головки. Длину прямого фланца необходимо учитывать при расчете смачиваемой площади цилиндрического сечения.

Том

Где,

для торсферических головок ASME:

для торсферических головок DIN 28011:

Рассчитанный объем не включает прямой фланец головки, только изогнутую часть.Длину прямого фланца необходимо учитывать при расчете объема цилиндрического сечения.

верх

Головки с выступом имеют самую низкую стоимость, но также и самое низкое расчетное давление, в отличие от торосферических или эллипсоидальных головок, у них нет поворотного кулака. Обычно они используются в атмосферных резервуарах, таких как горизонтальные резервуары для хранения жидкого топлива или автоцистерны.

Здесь мы представляем формулы для расчета смачиваемой площади и объема для произвольной высоты уровня жидкости в одной напорной головке с ударом.

Смачиваемая площадь

Мы можем аппроксимировать частично заполненную площадь поверхности ударной головки, используя формулу для эллиптических головок. Это приближение приведет к завышению оценки площади поверхности, что является консервативным для расчетов пожаротушения бассейна.

Объем

Уравнение для частично заполненного объема является приблизительным, но дает разумную точность для расчета объема резервуара.

Здесь представлены формулы для расчета смачиваемой площади и объема для произвольной высоты уровня жидкости в цилиндрической части горизонтального барабана.

Смачиваемая область

Объем

Если сосуд имеет торосферическую или эллипсоидальную головку, длина прямого фланца головки должна быть включена в длину цилиндрической секции при расчете объема или площади поверхности.

1. B Wiencke, 2009, Расчет частичного объема сосудов под давлением
2. R Doane, 2007, Точные области увлажнения для частично заполненных сосудов
3. E Ludwing, 1997, Прикладное проектирование процессов для химических и нефтехимических заводов ( Том 2)
4. E Weisstein, 2013, Цилиндрический сегмент.Материал из MathWorld

Статья создана: 1 марта 2013 г.

---

Теги статьи

Расчет объема напоров сосудов под давлением

Калькулятор объема напора
Галлонов США для цилиндрических головок
Измерения:
Головка Внутренний диаметр:	размеры в дюймах
Длина прямого фланца:	размеры в дюймах
Головка Тип:	Выберите тип головки ASME Фланцевый и выпуклый Стандартный Фланцевый и выпуклый 80:10 Фланцевый и угловой Полусферический эллиптический
ASME Фланцевые и шлифованные:	Блюдо Радиус = диаметр головки Радиус сустава = 6% диаметра головки
Стандартный Фланцевые и шлифованные:	Блюдо Радиус = диаметр головки Радиус сустава = от 3/4 дюйма до 2 дюймов в зависимости от на головке диаметром
80:10 Фланцевые и шлифованные:	Блюдо Радиус = 80% диаметра головки Радиус сустава = 10% диаметра головки
полусферическое:	Блюдо Радиус = 1/2 внутреннего диаметра головки Радиус сустава = N / A
Эллиптический:	Блюдо Радиус ≡ 90% диаметра головки Радиус сустава ≡ 17.3% диаметра головки
ASME:	10% Блюдо Радиус = диаметр головки Радиус сустава = 10% диаметра головки
Расчет Результатов:
Объем фланца прямого	Галлонов Литры
Объем головы (Есть ли не включает объем прямого фланца)	Галлонов Литры
Итого объем головы	Галлонов Литры
Затоплено объем	Галлонов Литры

Калькулятор объема резервуара для десяти различных форм резервуара

С помощью этого калькулятора объема резервуара вы можете легко оценить объем вашего резервуара.Выберите одну из девяти различных форм резервуаров: от стандартных прямоугольных и цилиндрических резервуаров до капсульных и эллиптических резервуаров. Вы даже можете найти объем усеченного конуса в резервуарах с коническим дном. Просто введите размеры вашего контейнера, и этот инструмент рассчитает общий объем резервуара для вас. Вы также можете указать высоту заполнения, которая будет использоваться для определения заполненного объема. Вам интересно, как это происходит? Прокрутите вниз, и вы найдете все необходимые формулы — объем капсульного резервуара, эллиптического резервуара или широко используемых резервуаров с коническим дном (иногда называемых коническими резервуарами), а также многое другое!

Ищете других цистерн различных форм и для другого применения? Воспользуйтесь нашим калькулятором объема, чтобы найти объем наиболее распространенных трехмерных твердых тел.Для чего-то более специализированного вы также можете взглянуть на калькуляторы объема аквариума и бассейна для решения повседневных проблем с объемом.

Калькулятор объема резервуара

Этот калькулятор объема резервуара — простой инструмент, который поможет вам определить объем резервуара, а также объем заполненной части. Вы можете выбрать одну из десяти форм резервуара:

• вертикальный цилиндр
• цилиндр горизонтальный
• призма прямоугольная (коробка)
• капсюль вертикальный
• горизонтальная капсула
• вертикальный овал (эллиптический)
• горизонтальный овал (эллиптический)
• конус нижний
• конус
• усеченный конус (усеченный конус, воронкообразный)

«Но как мне использовать этот калькулятор объема резервуара?», Спросите вы.Давайте посмотрим на простой пример:

1. Определитесь с формой . Предположим, что мы хотим найти объем вертикального резервуара-капсулы — выберите этот вариант из раскрывающегося списка. Схематическое изображение танка появится ниже; убедитесь, что это именно то, что вам нужно!
2. Введите размеры резервуара . В нашем случае нам нужно ввести длину и диаметр. В нашем примере они равны 30 и 24 дюйма соответственно. Дополнительно мы можем ввести высоту заливки — 32 дюйма.
3. Калькулятор объема бака уже нашел общий и залитый объем! Общий объем капсулы составляет 90,09 галлона США, а объем жидкости внутри составляет 54,84 галлона США. Как всегда, вы можете изменить единицы измерения, щелкнув сами единицы громкости. Очень просто!

Формула объема цилиндрического бака

Чтобы рассчитать общий объем цилиндрического резервуара, все, что нам нужно знать, это диаметр (или радиус) цилиндра и высота цилиндра (которую можно назвать длиной, если она расположена горизонтально).

Общий объем цилиндрического резервуара можно найти с помощью стандартной формулы объема — площади основания, умноженной на высоту. Круг — это форма основания, поэтому его площадь, согласно известному уравнению, равна π * радиус² . Таким образом, формула для определения объема резервуаров вертикального цилиндра выглядит так:

V_vertical_cylinder = π * радиус² * высота = π * (диаметр / 2) ² * высота

Если мы хотим вычислить заполненный объем, нам нужно найти объем «более короткого» цилиндра — это так просто!

V_vertical_cylinder = π * радиус² * заполнено = π * (диаметр / 2) ² * заполнено

Общий объем горизонтального цилиндрического резервуара можно найти аналогично — это площадь круглого конца, умноженная на длину цилиндра:

V_horizontal_cylinder = π * радиус² * длина = π * (диаметр / 2) ² * длина

Ситуация усложняется, когда мы хотим найти объем частично заполненного горизонтального цилиндра.Во-первых, нам нужно найти базовую площадь: площадь круглого сегмента, покрытого жидкостью:

Площадь сегмента = 0,5 * радиус² * (θ - sinθ)

, где θ — центральный угол сегмента, его можно найти по формуле для косинуса:

cos (θ / 2) = (радиус - заполненный) / радиус

θ = 2 * arccos ((радиус - заполненный) / радиус)

И, наконец, формула для частично заполненного горизонтального цилиндра:

V_horizontal_cylinder_filled = 0.5 * радиус² * (θ- sin (θ)) * длина , где θ = 2 * arccos ((радиус - закрашенный) / радиус)

Если баллон заполнен более чем наполовину, то легче вычесть пустую часть резервуара из общего объема.

Калькулятор объема прямоугольного резервуара (прямоугольная призма)

Если вам интересно, как рассчитать объем прямоугольного резервуара (также известного как кубоид, коробка или прямоугольный шестигранник), не смотрите дальше! Вы можете знать этот резервуар как прямоугольный резервуар , но это не его собственное название, поскольку прямоугольник представляет собой 2D-форму, поэтому у него нет объема.

Чтобы найти объем прямоугольной призмы, умножьте все размеры резервуара:

V_ rectangular_prism = высота * ширина * длина

Если вы хотите узнать, каков объем жидкости в резервуаре, просто измените переменную height на , заполненную в формуле объема прямоугольного резервуара:

V_rectangular_prism_filled = заполненное * ширина * длина

Для этого калькулятора объема резервуара не имеет значения, находится ли резервуар в горизонтальном или вертикальном положении.Просто убедитесь, что с заливкой и высотой расположены вдоль одной оси.

Формула объема капсулы

Наш инструмент определяет капсулу как две полусферы, разделенные цилиндром. Чтобы рассчитать общий объем капсулы, все, что вам нужно сделать, это добавить объем сферы к цилиндрической части:

V_capsule = π * (диаметр / 2) ² * ((4/3) * (диаметр / 2) + длина)

В зависимости от положения резервуара расчет заполненного объема будет немного отличаться:

1.Для горизонтального капсульного бака

Поскольку полусферы на обоих концах резервуара идентичны, они образуют сферическую крышку — добавьте эту часть к части из горизонтального цилиндра (см. Параграф выше), чтобы рассчитать объем жидкости:

капсула_h_filled = V_horizontal_cylinder_filled + V_spherical_cap_filled = 0,5 * (диаметр / 2) ² * (θ- sin (θ)) * длина + ((π * заполнено²) / 3) * ((1,5 * диаметр) - заполнено)

2. Для вертикального капсульного бака

Формула различается для разной высоты заполнения:

• если заполнен <диаметр / 2 , то жидкость находится только в нижней части полусферы, поэтому нам нужен только объем по формуле сферической крышки:

V_capsule_filled = ((π * заполнено²) / 3) * ((1.5 * диаметр) - заполненный)

• если диаметр / 2 <заполненный <диаметр / 2 + длина , то нам нужно добавить объем полусферы и «более короткий» цилиндр:

V_capsule_filled = (2/3) * π * (диаметр / 2) ³ + π * (диаметр / 2) ² * (заполненный - диаметр / 2)

• , если диаметр /2 + длина <заполнено , это означает, что у нас есть полная нижняя полусфера и цилиндр, поэтому нам просто нужно вычесть сферическую крышку (пустую часть) из всего объема:

V_capsule_filled = V_capsule - ((π * заполнено²) / 3) * ((1.5 * диаметр) - (длина + диаметр - заполненный)))

Объем эллиптического резервуара (овальный резервуар)

В нашем калькуляторе мы определяем овальный резервуар как цилиндрический резервуар с эллиптическим концом (не имеющий форму стадиона, как его иногда определяют). Чтобы найти общий объем эллиптического резервуара, вам нужно умножить площадь эллипса на длину резервуара:

V_ellipse = π * ширина * длина * высота / 4

Наконец, еще одна простая формула! К сожалению, определить объем частично заполненного резервуара — как в горизонтальном, так и в вертикальном положении — не так просто.Вам нужно использовать формулу для площади сегмента эллипса и умножить результат на длину резервуара:

V_ellipse_filled = длина * высота * ширина / 4 * (arccos (1 - (2 * заполнено / высота)) - (1 - (2 * заполнено / высота)) * √ (4 * заполнено / высота - 4 * заполнено ² / высота²))

Объем ствола — резервуар в форме усеченного конуса

Для расчета объема усеченного конуса используйте формулу:

V_frustum = (1/3) * π * cone_height * ((Diameter_top / 2) ² + (Diameter_top / 2) * (Diameter_bottom / 2) + (Diameter_bottom / 2) ²)

Если вы хотите найти частично заполненный объем усеченной пирамиды для заданной высоты заполнения, сначала вычислите верхний радиус заполненной части:

R = 0.5 * верхний_диаметр * (заполненный + z) / (cone_height + z)

где

z = высота_конуса * нижний_диаметр / (верхний_диаметр - нижний_диаметр)

(Вы можете получить формулу из подобия треугольников)

После этого просто найдите новый том усеченной пирамиды:

V_frustum_filled = (1/3) * π * cone_height * (R² + R * (диаметр_bottom / 2) + (dia_bottom / 2) ²)

Объем резервуара с коническим дном (конический резервуар) и резервуары с коническим верхом

Найти общий объем резервуара с коническим дном не так сложно — просто добавьте объем усеченной части к объему цилиндрической части:

V_cone_bottom = V_frustum + V_cylinder = (1/3) * π * cone_height * ((Diameter_top / 2) ² + (Diameter_top / 2) * (Diameter_bot / 2) + (Diameter_bot / 2) ²) + π * (диаметр_top / 2) ² * высота_цилиндра

Чтобы рассчитать частично заполненный резервуар, просто добавьте часть усеченного конуса и часть цилиндра, в зависимости от уровня заполненной жидкости, используя приведенные выше уравнения.

Расчет общего объема резервуара с коническим верхом точно такой же, как и для резервуара с коническим дном. Единственная разница в том, когда вы хотите найти заполненную часть — разумеется, сначала заполняется цилиндрическая часть, а уже потом усеченная часть.

Эллиптическая головка — обзор

3.1 Характеристики растения и способы его выращивания

Сорго сладкое относится к семейству злаковых. Растение вырастает до 4 м в высоту. Как и у других трав, корни мочковатые и обильно разветвляются в подходящей среде.Придаточные корни образуются из надземных узлов, обеспечивая защиту растения от полегания. Побеги развиваются из желобчатого, почти овального стебля. В дальнейшем из каждого побега развивается самостоятельная корневая система [22]. Стебель является неотъемлемой частью производства этанола из-за высокой концентрации легко ферментируемых сахаров. Спелое сладкое сорго состоит примерно из 75% тростника, 10% листьев, 10% корней и 5% семян по весу [21]. Урожайность как растворимых, так и нерастворимых углеводов из стеблей сладкого сорго определяется его сортом, годом и временем сбора урожая.

Сорго сладкое — растение C ₄ , имеющее широкие плоские листья и круглую или эллиптическую головку. Это очень засухоустойчивая и наиболее эффективная культура засушливых земель для преобразования атмосферного CO ₂ в сахар [22]. Он известен как сахарный тростник пустыни, а также верблюжий урожай [23]. Его можно легко культивировать в тропических, субтропических и умеренных регионах, но в основном его выращивают в полузасушливых тропиках мира [24,25]. Он очень податлив по своей природе, потому что может пережить засушливые периоды и возобновить рост после дождя.Он может выдерживать экстремальную влажность лучше, чем большинство зерновых культур, особенно кукуруза. Сорго также может выживать и расти в условиях затопления, хотя и не очень хорошо; кукуруза, напротив, умрет. В другом исследовании результат воздействия различных факторов, таких как транспирация, скорость обмена углерода (CER), доля транспирации (CER / транспирация), водный потенциал листьев, диффузионная устойчивость листьев и осмотическая модификация, продемонстрировали общую закономерность более заметной засухоустойчивости сорго, чем в просе, показывая, что обычно наблюдаемая адаптация проса к засушливым условиям может происходить из-за различных компонентов, например, предотвращения засухи или устойчивости к жаре [26].Сорго — пятая по значимости зерновая культура в мире [27] после пшеницы, риса, кукурузы и ячменя. Индия занимает первое место по площади и третье по производству сорго [22]. Сладкое сорго может переносить широкий спектр почвенных условий, от тяжелых глинистых почв до легких песков, с pH от 5,0 до 8,5 [28] и средне-высоким питательным статусом (N ≥ 260, P ≥ 12 и K ≥ 120 кг га ^-1 ). Ему требуется менее 50% общего азота для производства этанола, аналогичного кукурузе [29], и он способен удалять 62% общего азота без разницы в выходе сухого вещества [30].Оптимальные физические характеристики почвы для выращивания сладкого сорго: органическое вещество> 0,6%, глубина> 80 см, насыпная плотность <1,4 мг · м ^-3 и водоудерживающая способность> 50% от полевой урожайности [22].

Урожай можно выращивать между 40˚ и 40 ^˚ южной широты [31], на высоте 900–1500 м в африканских странах и до 2500 м в Мексике. Эта культура имеет вегетационный период 4–5 месяцев и требует нормы высева 8 кг / га для получения хорошего урожая, составляющего около 100 000–120 000 растений / га.Сорго сладкое можно выращивать при температуре 12–37 ˚C, оптимальной для роста и фотосинтеза является 32–34 ˚C; продолжительность дня 10–14 ч и диапазон относительной влажности 15–50% [22]. Эта культура имеет низкую потребность в воде по сравнению с кукурузой [32] и может нормально выращиваться в богарных условиях в районах, где выпадает 500-800 мм осадков. Однако стадии инициации метелки и загрузки являются критическими стадиями, чувствительными к влаге [31].

Хотя сладкое сорго относится к растениям короткого дня, сорта различаются по чувствительности к световому периоду [33,34].Репродуктивный рост (т.е. цветение) сорго, чувствительных к фотопериоду, наблюдается, когда длина дня достигает определенного порога (обычно от 11,5 до 13,5 часов) [35]. Эллис и др. [36] изучали влияние фотопериода, температуры и асинхронности между термопериодом и фотопериодом на развитие и инициирование метелки у сорго, и оказалось, что это начальная нечувствительная к фотопериоду, но чувствительная к температуре фаза (ювенильная фаза), за которой следует чувствительная к фотопериоду, но нечувствительная к температуре фаза, а затем последняя фаза, нечувствительная как к фотопериоду, так и к температуре.Сорго является количественным растением короткого дня, основная вегетативная фаза состоит из двух стадий, а именно: ювенильной стадии (зависит от температуры) и индуктивной стадии (зависит от фотопериода). Требование к теплу генотипа должно быть выполнено до того, как он отреагирует на фотопериод. Цветение тропических сортов задерживается более чем на 11,1–12,6 ч, и когда длина дня становится короче (<12 ч), растение сорго переходит от вегетативной стадии к репродуктивной [37]. Folliard et al. [38] сообщили, что время от появления всходов до зарождения пика уменьшилось с 54 до 22 дней при 2-минутном изменении продолжительности дня, и оценили время до зарождения метелки (PI) у высокочувствительного к фотопериоду сорта гвинейского сорго CSM-388.Точно так же существуют сорго, нечувствительные к фотопериоду. Репродуктивное развитие или рост было замечено у таких сорго через определенный промежуток времени, независимо от продолжительности светового дня [35]. Начало цветения, знаменующее конец вегетативного роста, происходит через 30–40 дней после прорастания. За грандиозным периодом роста следует формирование цветочной почки, состоящей в основном из увеличения клеток. Цветение тропического сладкого сорго начинается через 55–70 дней после посева. Но для метелки сорго умеренного климата всходы откладываются на 20–30 дней, так как период роста урожая более длительный (5 месяцев).За зарождением метелки следует цветение и опыление. Цветки начинают распускаться через 2 дня после полного появления метелки, а максимальное цветение наступает через 3–4 дня после начала цветения [39].

Сорт сладкого сорго выращивают во всем мире. Крупнейшим производителем сорго в мире по площади является Индия (7,5 млн га), за ней следуют Нигерия (7,6 млн га) и Судан (6,6 млн га). Но по производству Индия занимает третье место после США и Нигерии. Он хорошо адаптирован к полузасушливым тропикам и является наиболее эффективной и устойчивой культурой засушливых земель для преобразования атмосферного CO ₂ в сахар [40].

Объем горизонтального цилиндра

Как мы можем определить объем цилиндра, подобного этому, если мы знаем только его длину и радиус и насколько высоко он заполнен?

Сначала прорабатываем область на одном конце (объяснение ниже):

Площадь = cos ^-1 ( r — h r ) r ² — (r — h) √ (2rh — h ² )

Где:

• r — радиус цилиндра
• h — высота цилиндр заполнен до

А затем умножьте на длину, чтобы получить объем:

Объем = Площадь × Длина

Зачем сначала рассчитывать площадь? Итак, мы можем проверить, является ли это разумным значением! Мы можем нарисовать квадраты на реальном танке и посмотреть, соответствует ли область реальному миру, или просто подумать, как эта область сравнивается с полным кругом.

Калькулятор

Введите значения радиуса, высоты с заливкой и длины, ответ рассчитывается «в реальном времени»:

Формула площади

Как мы получили эту формулу площади?

Это площадь сектора (область пирога-ломтика) за вычетом треугольной части.

Площадь сегмента = Площадь сектора — Площадь треугольника

Глядя на эту диаграмму:

Используя немного геометрии, мы можем вычислить, что угол θ / 2 = cos ^-1 ( r — h r ), поэтому

Площадь сектора = cos ^-1 ( r — h r ) r ²

А для полутреугольника высота = (r — h) , а основание может быть вычислено с помощью Пифагора:

• b ² = r ² — (r − h) ²
• b ² = r ² — (r ² −2rh + h ² )
• b ² = 2rh — h ²
• b = √ (2rh — h ² )

Таким образом, этот полутреугольник имеет площадь ½ (высота × основание), поэтому для полного треугольника:

Площадь треугольника = (r — h) √ (2rh — h ² )

Итак:

Площадь сегмента = cos ^-1 ( r — h r ) r ² — (r — h) √ (2rh — h ² )

Калькулятор объема резервуара

— Дюймовый калькулятор

Выберите стиль бака и его размеры, чтобы рассчитать вместимость.При желании введите глубину заполнения, чтобы рассчитать объем жидкости в резервуаре.

Как рассчитать объем резервуара

Объем или вместимость бака можно определить за несколько простых шагов. Конечно, калькулятор выше — самый простой способ рассчитать объем резервуара, но следуйте инструкциям, чтобы узнать, как рассчитать его самостоятельно.

Шаг первый: Измерьте резервуар

Первым делом необходимо измерить основные размеры резервуара. Для круглых резервуаров найдите диаметр и длину или высоту.Для прямоугольника или куба найдите длину, ширину и высоту.

Шаг второй: Найдите формулу объема резервуара

Для расчета вместимости резервуара потребуется формула объема. Формула объема зависит от типа измеряемого резервуара. Ознакомьтесь с приведенными ниже формулами и выберите ту, которая подходит вашему стилю.

Формула цилиндрового бака

объем бака = π × r ² × л

r = радиус (диаметр ÷ 2)
l = длина (или высота для вертикального резервуара)

---

Овальный резервуар Formula

площадь = ((в — ш) × ш) + (π × r ² )
объем резервуара = площадь × л

r = радиус (ширина резервуара ÷ 2)
w = ширина
l = длина
h = высота

---

Капсульный резервуар Formula

объем цилиндра = π × r ² × l
объем сферы = 4/3 π × r ³
объем резервуара = объем цилиндра + объем сферы

r = радиус (диаметр ÷ 2)
l = длина (или высота для вертикального резервуара)

---

Прямоугольный резервуар Formula

объем резервуара = д × ш × в

l = длина
w = ширина
h = высота

---

Не нашли формулу формы вашего танка? Найдите еще больше формул объема.

Шаг третий: решите формулу объема

Когда у вас есть размеры резервуара и соответствующая формула для вычисления объема, просто введите размеры в формулу и решите.

Например, , давайте найдем объем цилиндра диаметром 36 дюймов и длиной 72 дюйма.

радиус = 36 ″ ÷ 2
радиус = 18 ″

объем резервуара = π × 18 ² × 72
объем резервуара = 73 287 куб. дюймов

Таким образом, объем этого бака составляет 73 287 кубических дюймов.

Шаг четвертый: преобразование единиц объема

Результирующий объем резервуара будет иметь кубическую форму первоначальных измерений. Например, если первоначальные измерения резервуара были в дюймах, то измерение объема будет в кубических дюймах. Часто требуются другие формы объема, такие как галлоны или литры.

Таким образом, последний шаг — это преобразование одного измерения объема в желаемую единицу результата. Попробуйте наши калькуляторы преобразования объема, чтобы преобразовать результаты.

Точная оценка объема сосуда по изображениям профиля на JSTOR

Абстрактный

Высокая фрагментированность большинства археологических керамических комплексов делает ценные или реконструируемые сосуды ценными и редкими находками. Объем сосуда редко подвергался систематической количественной оценке из-за отсутствия удобных методов реконструкции, относящихся к осколкам и частичным сосудам. Теперь с помощью метода, представленного в этой статье, можно с высокой точностью рассчитать объемную вместимость фрагментированных сосудов на основе тщательно подготовленных иллюстраций профиля сосуда.Профиль оцифровывается с использованием небольшого количества точек на сосуд (обычно достаточно от 20 до 30 точек). Затем эти данные преобразуются в объемную меру с использованием компьютеризированного алгоритма, основанного на геометрии уложенных друг на друга цилиндров со скошенными стенками. Этот метод определения объемов сосудов был протестирован и показал высокую повторяемость и точность. Поддающиеся количественной оценке источники ошибок обычно не превышают одного процента на сосуд, а конечная точность ограничивается главным образом качеством иллюстрации.С помощью этой компьютеризированной техники фрагментированные сосуды больше не нужно полностью реконструировать, чтобы получить объемную информацию.

Информация о журнале

С 1935 года компания American Antiquity опубликовала оригинальные статьи по археологии Нового Света, а также по археологическим методам, теории и практике во всем мире. Начиная с 1990 года, большинство статей по археологии и предыстории Латинской Америки публикуется в Латиноамериканском обществе античности Америки.

Информация об издателе

Cambridge University Press (www.cambridge.org) — издательское подразделение Кембриджского университета, одного из ведущих исследовательских институтов мира, лауреата 81 Нобелевской премии. В соответствии со своим уставом издательство Cambridge University Press стремится максимально широко распространять знания по всему миру. Он издает более 2500 книг в год для распространения в более чем 200 странах. Cambridge Journals издает более 250 рецензируемых научных журналов по широкому спектру предметных областей в печатных и онлайн-версиях.Многие из этих журналов являются ведущими научными публикациями в своих областях, и вместе они составляют одну из наиболее ценных и всеобъемлющих областей исследований, доступных сегодня. Для получения дополнительной информации посетите http://journals.cambridge.org.

.