Объём стенки цилиндра — онлайн калькулятор
Чтобы посчитать объём стенки цилиндра, то есть объём полого цилиндра, воспользуйтесь нашим очень удобным онлайн калькулятором:
Онлайн калькулятор
Найти чему равен объём полого цилиндра (Vст) можно зная (либо-либо):
- Высоту цилиндра h, внешний радиус r1 и внутренний радиус r2
- Высоту цилиндра h, внешний диаметр d1 и внутренний диаметр d2
- Высоту цилиндра h, внешний радиус r1 и толщину стенки δ
- Высоту цилиндра h, внутренний радиус r2 и толщину стенки δ
- Высоту цилиндра h, внешний диаметр d1 и толщину стенки δ
- Высоту цилиндра h, внутренний диаметр d2 и толщину стенки δ
Зная оба радиуса (диаметра)
Зная толщину стенки
Теория
Чему равен объём полого цилиндра
Формулы
Через радиусы или диаметры цилиндра
Vст = π ⋅ (r1² — r2²) ⋅ h , где r1 — внешний радиус, r2 — внутренний радиус , а h — высота
Vст = π ⋅ ((d1/2)² — (d2/2)²) ⋅ h , где d1 — внешний диаметр, d2 — внутренний диаметр, а h — высота
Через толщину стенки цилиндра
Vст = π ⋅ (d2 ⋅ δ + δ²) ⋅ h , где δ — толщина стенки цилиндра, d2 — внутренний диаметр, а h — высота
Vст = π ⋅ ((d1 — 2 ⋅ δ) ⋅ δ + δ²) ⋅ h , где δ — толщина стенки цилиндра,
Vст = π ⋅ (2 ⋅ r2 ⋅ δ + δ²) ⋅ h , где δ — толщина стенки цилиндра, r2 — внутренний радиус, а h — высота
Vст = π ⋅ ((2 ⋅ r1 — 2 ⋅ δ) ⋅ δ + δ²) ⋅ h , где δ — толщина стенки цилиндра, r1 — внешний радиус, а h — высота
Пример №1
К примеру, посчитаем каков объём металла в трубе, если её длинна 3 метра, внешний диаметр d1=5 см, а внутренний d2=4. 5 см?
5 см?
Vст = 3.14 ⋅ ((5/2)² — (
Пример №2
Теперь посчитаем объём металла в этой же 3-х метровой трубе, но возьмём внутренний радиус r2 = 2.25 см и толщину стенки δ = 0.25 см (при этом у нас должен получится тот же ответ, что и в предыдущем примере):
Vст = 3.14 ⋅ (2 ⋅ 2.25 ⋅ 0.25 + 0.25²) ⋅ 300 = 3.14 ⋅ 1.1875 ⋅ 300 ≈ 1119 см³
См. также
Объем полого цилиндра
Объем полого цилиндра, формулы для вычисления объема и площадей правильного полого цилиндра.
Формула вычисления объема полого цилиндра часто применяются при расчете массы полой круглой трубы. Для вычисления массы трубы, необходимо вычисленный объем трубы (полого цилиндра) умножить на плотность материала из которого изготовлена труба (цилиндр).
Расчет площади поверхностей цилиндра, иногда необходим для определения расхода материала для нанесения защитного покрытия трубы (полого цилиндра).
Объем полого цилиндра, вычисленный через внутренний и наружный радиусы
r1 — внешний радиус
r2 — внутренний радиус
h — высота цилиндра
… вычисление …
Площадь основания… вычисление …
Общая площадь… вычисление …
Объем полого цилиндра по толщине стенки и наружному диаметру
D — внешний диаметр
δ — толщина стенки
h — высота цилиндра
. .. вычисление …
.. вычисление …
… вычисление …
Общая площадь поверностей… вычисление …
Объем полого цилиндра, вычисляемый по внутреннему диаметру и толщине стенки
d — внутренний диаметр
δ — толщина стенки
h — высота цилиндра
… вычисление …
Упрощение формулы:
Площадь основания… вычисление …
Площадь внутренней и внешней боковой поверхности… вычисление …
Упрощение формулы:
Общая площадь поверностей
. .. вычисление …
.. вычисление …
Различия между разными видами цилиндров, а также со свойствами правильного цилиндра, можно ознакомиться в статье «Объем цилиндра» в разделе« Теория».
Объем и площадь других видов цилиндров рассмотрен в статьях:
Объем цилиндра
Объем части цилиндра
Объем части полого цилиндра
Вы можете скачать формулы объема и площади поверхностей правильного полого цилиндра в виде картинки.
скачать скачать скачать скачать скачать скачатьОбъем цилиндра: онлайн калькулятор, формулы, примеры решений
Круговой прямой цилиндр (от греч. kylindros, валик, каток) представляет собой геометрическую фигуру, которая образована путем вращения прямоугольника вокруг одной из своих сторон. Это наиболее распространенный вид цилиндра, который часто встречается в реальной жизни.
kylindros, валик, каток) представляет собой геометрическую фигуру, которая образована путем вращения прямоугольника вокруг одной из своих сторон. Это наиболее распространенный вид цилиндра, который часто встречается в реальной жизни.
Геометрия цилиндра
Помимо кругового цилиндра существует большое разнообразие других геометрических тел, которые представляют собой соединение цилиндрической поверхности и оснований. Цилиндрическая поверхность — это поверхность, созданная путем движения прямой образующей линии вдоль направляющей кривой. Направляющая кривая может иметь различные формы. Если направляющая — окружность, то образующая при движении формирует классический круговой цилиндр. Однако направляющая может принимать форму параболы, эллипса, гиперболы, произвольной или даже бесконечной кривой. В этом случае цилиндр будет называться соответственно параболическим, эллиптическим, гиперболическим или бесконечным.
В принципе, любое тело, ограниченное цилиндрической поверхностью, называется цилиндром, однако на практике в подавляющем большинстве случаев мы имеем дело с круговым прямым цилиндром. Цилиндрическую форму имеет множество реальных объектов, к примеру, консервные банки, цистерны, чертежные тубусы, водопроводные трубы, архитектурные колонны или поршни двигателя внутреннего сгорания. Кроме того, цилиндрическую форму имеют различные детали, такие как болты, втулки, заклепки или цевки, поэтому на производстве важно свободно оперировать такими параметрами деталей как объем или площадь поверхности.
Цилиндрическую форму имеет множество реальных объектов, к примеру, консервные банки, цистерны, чертежные тубусы, водопроводные трубы, архитектурные колонны или поршни двигателя внутреннего сгорания. Кроме того, цилиндрическую форму имеют различные детали, такие как болты, втулки, заклепки или цевки, поэтому на производстве важно свободно оперировать такими параметрами деталей как объем или площадь поверхности.
Объем цилиндра
Что представляет собой объем кругового цилиндра? Представьте, что вы печете блинчики. Первый блин комом, а вот второй уже имеет вид круга — плоскости, ограниченной окружностью. В идеале этот блинчик очень тонкий и не имеет никакого объема. Однако вы складываете третий, четвертый, десятый блинчик в стопку и ваш круг набирает высоту и приобретает некий объем. Для вычисления полученного объема вы должны определить площадь одного блинчика и их количество, то есть высоту получившейся стопки.
Площадь одного блинчика определяется по простой формуле:
S = pi × R2,
где R – радиус блина.
Таким образом, объем блинной стопки рассчитывается как:
V = pi × R2 × h
Определение объема цилиндра может вам пригодиться не только при решении школьных задач, но и в реальных ситуациях. Для вычислений используйте наш онлайн-калькулятор, который мгновенно представит результат в удобной форме. Вам понадобится узнать только две переменные: высоту цилиндра и его радиус (диаметр). Рассмотрим примеры.
Примеры
Быт
К примеру, у вас на даче стоит цистерна для питьевой воды и вам нужно набрать колодезную воду для ее наполнения. Однако на цистерне не указан ее объем, и чтобы не накачать лишнего или не возвращаться лишний раз за водой, вам необходимо определить объем бака. К счастью, цистерна представляет собой прямой круговой цилиндр и для определения объема вам необходимо узнать только ее диаметр d = 1 м и высоту h = 1 м. Введите эти данные в онлайн-калькулятор и получите ответ в виде:
V = 0,261
Таким образом, объем цистерны составляет 0,261 кубометров или 261 литр. Зная объем стандартного кега для воды (19 л), вам становится ясно, что от колодца до цистерны вам придется ходить 14 раз, поэтому для наполнения цистерны проще использовать шланг.
Зная объем стандартного кега для воды (19 л), вам становится ясно, что от колодца до цистерны вам придется ходить 14 раз, поэтому для наполнения цистерны проще использовать шланг.
Работа
Допустим, вы проектируете систему отопления и вам необходимо узнать, сколько воды будет проходить по трубам в каждый момент времени. Объем воды в отопительной трубе равен произведению длины трубы на объем жидкости, который приходится на 1 метр трубопроводного изделия. По сути, вам необходимо вычислить объем цилиндрической трубки. Пусть такая труба имеет параметры R = 10 см = 0,10 м, а h = 1 м. Введите эти параметры в форму онлайн-калькулятора и получите результат в виде:
V = 0,0105
Следовательно, объем воды в таком цилиндре составит 0,0105 кубометров или 10,5 литров. Собирая отопительную систему из стандартных трубок, вы сможете узнать, сколько воды понадобится для ее функционирования.
Заключение
Круговые цилиндры — это самый распространенный тип цилиндрических фигур. Расчет параметров геометрических тел необходим специалистам, которые работают с цилиндрическими деталями, трубами или цистернами. В быту определение объемов цилиндров может пригодиться при ремонте, приготовлении пищи или консервации овощей. Кроме того, наш онлайн-калькулятор пригодится также и учащимся, которые только пробуют определять объемы тел вращения.
Расчет параметров геометрических тел необходим специалистам, которые работают с цилиндрическими деталями, трубами или цистернами. В быту определение объемов цилиндров может пригодиться при ремонте, приготовлении пищи или консервации овощей. Кроме того, наш онлайн-калькулятор пригодится также и учащимся, которые только пробуют определять объемы тел вращения.
Объем цилиндра через площадь основания и высоту — онлайн калькулятор
При других вводных ищите способы решения в наборе программ на сайте. Здесь собраны расчеты по всем темам из программы по алгебре и геометрии.
Нахождение объема цилиндра онлайн-калькулятором по площади основания и высоте
Программа автоматически находит объем цилиндра по формуле:
где S – площадь основания фигуры,
h – высота.
Предварительная регистрация на сайте для выполнения расчетов не требуется. Также сервис не понадобится оплачивать. Запросы на вычисления можно совершать столько раз, сколько требуется для усвоения материала. Лимита нет.
Кому пригодится калькулятор:
- Студентам во время зачетов и экзаменов. Формула для решения задачи, подробные действия и ответ без погрешностей помогут во время проверки знаний.
- Школьникам, выполняющим домашнее задание. Понятный интерфейс с чертежом позволяет лучше усвоить материал. Набор программ поможет не только разобраться в новой теме, но и подготовиться к поступлению в университет.
- Преподавателям. Проверку работ учащихся и планирование уроков, включающих индивидуальные задания, теперь можно делать быстрее.

Расчеты также помогут родителям, специалистам инженерного профиля, строителям. В бытовых ситуациях быстрые вычисления незаменимы.
Если вы не смогли найти нужную программу или столкнулись с объемным заданием, свяжитесь с консультантом. Он предложит недорогую услугу по объяснению темы и найдет для этого опытного преподавателя из нашей компании.
| Радиус: | ||
| Высота: | ||
Цилиндр – геометрическое тело, которое получается при вращении прямоугольника вокруг его стороны. Формула объема цилиндра: , где R – радиус оснований, h – высота цилиндра | ||
| Тип: | Профиль: | Толщина (мм): |
| Трехслойный гофрокартон | B | 3 |
| Трехслойный гофрокартон | C | 3,7 |
| Трехслойный гофрокартон | E | 1,6 |
| Пятислойный гофрокартон | BC | 7 |
| Пятислойный гофрокартон | BE | 4 |
Перемножив полученные значения, получим объем коробки в кубических метрах. Чтобы получить результат в литрах необходимо полученное значение в м3 умножить на 1000.
Подсчет объема коробки в литрах
При транспортировке мелких или сыпучих товаров их также пакуют в ящики. Учитывая, что такие предметы и материалы занимают весь объем тары, нужно знать их количество в литрах. Если Вы интересуетесь, как посчитать объем короба в литрах, определяйте литраж следующим образом:
Если Вы интересуетесь, как посчитать объем короба в литрах, определяйте литраж следующим образом:
находим кубатуру V=a*b*h =0,3*0,25*0,15=0,0112 м3 >;
зная равенство: 1 м3 = 1000 л, переводим полученное значение в литры: V=0,0112 *1000=1,2 л.
Объем цилиндрической полости
Объем полости в виде цилиндра равен объему цилиндра, который извлечен из данной полости для ее образования. То есть для вычисления цилиндрической полости можно воспользоваться формулами и калькулятором для расчета простого правильного цилиндра в зависимости от известных исходных данных.
На картинке продемонстрирована цилиндрическая полость, образованная в теле путем извлечения из него цилиндра. Объем извлеченного цилиндра и объем образованной полости равны.
Нужно отметить один важный момент. Несмотря на равенство объемов извлеченного цилиндра и образованной полости, площади поверхностей данных объектов будут отличаться, так как у образованной цилиндрической полости отсутствует верхняя поверхность. То есть суммарная площадь поверхности образованной цилиндрической полости будет меньше суммарной площади извлеченного цилиндра на одну площадь основания цилиндра.
То есть суммарная площадь поверхности образованной цилиндрической полости будет меньше суммарной площади извлеченного цилиндра на одну площадь основания цилиндра.
Теория
Цилиндр может быть правильным или наклонным
Правильный цилиндр – это цилиндр, где угол между образующими боковой поверхности и основанием цилиндра равен 90 градусов.
Неправильный или наклонный цилиндр – это цилиндр, где угол между образующими боковой поверхности и основанием цилиндра отличается от 90 градусов.
Рассмотрим правильный цилиндр.
Цилиндр – это тело, образованное вращением прямоугольника вокруг одной из его сторон. Тело цилиндра ограничено двумя кругами, называемыми основанием цилиндра и боковой цилиндрической поверхностью, которая в развертке представляет собой прямоугольник
Цилиндр можно так же описать как тело, состоящее из двух равных кругов, не лежащих в одной плоскости и параллельных между собой, и отрезков, соединяющих все точки одной окружности, с соответствующими точками другой окружности.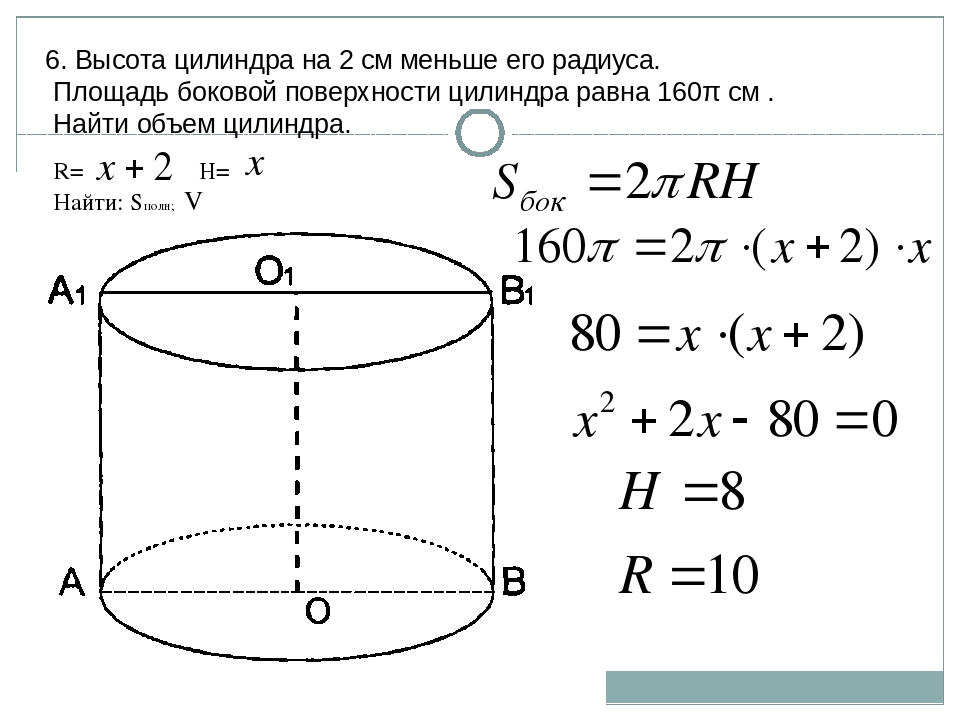 Данные отрезки называются образующими цилиндра.
Данные отрезки называются образующими цилиндра.
Радиус основания цилиндра, является радиусом цилиндра.
Ось цилиндра – это прямая, соединяющая центра оснований цилиндра.
Высота цилиндра – это перпендикуляр, опущенный от одного основания цилиндра к другому.
Объем прямого цилиндра
Цилиндр – это геометрическое тело, которое сформировано вращением прямоугольника на оси, совпадающей с одним из его сторон. Слово «цилиндр» происходит от греческого слова «kylindros».
Объем цилиндра через площадь основания и высоту цилиндра
Объем цилиндра равен произведению площади основания цилиндра на его высоту.
[ LARGE V = S cdot H ]
где:
V – объем цилиндра
H – высота цилиндра
S – площадь цилиндра
Поверхности цилиндра
Наружную поверхность цилиндра можно условно разделить на три отдельные поверхности: верхняя, нижняя и боковая.
Верхняя и нижняя поверхности цилиндра имеют форму круга и равны между собой.
Боковая поверхность цилиндра имеет форму прямоугольника. Чтобы это наглядно представить, возьмем боковую наружную поверхность цилиндра и мысленно сделаем вертикальный разрез по образующей цилиндра. Далее развернем поверхность на плоскость. В результате увидим, что боковая поверхность имеет форму прямоугольника (см. на картинке).
Сечения цилиндра
При сечении цилиндра плоскостью, проходящей через оба основания цилиндра под углом в 90 градусов, всегда получатся прямоугольная фигура
При сечении цилиндра плоскостью, проходящей через оба основания цилиндра под углом отличным от 90 градусов, получатся фигура, похожая на прямоугольник, но две боковые стороны которого будут являться кривыми линиями.
Если секущая поверхность проходит параллельно основаниям цилиндра, то сечением будет круг
Если секущая поверхность проходит через боковую поверхность, но при этом не параллельна основанию цилиндра, то в сечении получается эллипс
Если секущая поверхность проходит через одно основание цилиндра и боковую поверхность, то в сечение будет фигура в виде половины эллипса
Как рассчитать объем цилиндра с помощью калькулятора
Калькулятор позволяет определить объем цилиндра по одному из 3 вариантов:
- площадь основания и высота цилиндра;
- радиус основания и высота цилиндра;
- диаметр основания и высота цилиндра.

Выберите соответствующий шаг и введите исходные данные в соответствующие поля.
Также важно указать единицы измерения по условиям задачи.
Расчеты будут выполнены автоматически и конвертированы в основные метрические физические величины объема.
Формула расчета объема цилиндра
Объем цилиндра вычисляется как произведение площади основания на высоту цилиндра. Так как основанием цилиндра является круг, площадь основания можно рассчитать через радиус или диаметр.
Найти объем цилиндра
Выберите известные величины:Введите данные:
Вводить можно числа или дроби (-2.4, 5/7, …).
Источники
- https://ru.onlinemschool.com/math/formula/volume/
- https://mnogoformul.ru/obem-cilindra
- https://poschitat.online/obem-cilindra
- https://MicroExcel.ru/obyom-tsilindra/
- https://www.calc.ru/obyem-tsilindra.html
- https://gofro-karton.com/blog/rasschitat_obem_korobki/
- https://tara-tovara.
 ru/docs/poleznaya_inform/kak_rasschitat_obem_korobki_v_m3_i_litrakh/
ru/docs/poleznaya_inform/kak_rasschitat_obem_korobki_v_m3_i_litrakh/ - https://doza.pro/art/math/geometry/cylinder
- https://calcsbox.com/post/formula-obema-cilindra.html
- https://kalkulyator-nds.com/obem-cilindra-kalkulyator
- https://ru.onlinemschool.com/math/assistance/figures_volume/cylinder/
периметр, площадь, содержание (формула и онлайн-расчет)
Расчет
Введите значения в желтые поля — другие отсчитывает себя.
При изменении информации в полях, отмеченные автоматически пересчитывается.
В качестве десятичной запятой можно использовать как запятую, так и точку.
Результат выводится в тех-же единицах, что и вводите данные.
Например если ввели в дециметрах, то и результат будет в них-же.
Обнаруженны NaN, проверьте, что вы ввели в поле
корректные данные, то есть без букв и других символов.
Формулы
| Диаметр | d = | 2 r | [m] |
| Окружность цилиндра | O = | π d = 2 π r | [m] |
| Площадь одной базы | P = | π d²/4 = π r² | [m²] |
| Поверхность цилиндра | Q = | π d h = 2 π r h | [m²] |
| Общая площадь | S = | 2 P + Q = 2 π r (r + h) | [m²] |
| Объем | V = | π d²/4 h = π r² h | [m³] |
r … радиус = ½ диаметра
d … диаметр = 2 радиус
h … высота цилиндра
S … центр базовые цилиндра
o … ось цилиндра
π (Пи) = 3,14 (примерно)
Цилиндр и призмы
Скоро.
Принцип расчета
Общая площадь цилиндра состоит из поверхностей как основания и кожуха цилиндра. Оболочка цилиндра является произведением высоты и окружности цилиндра
Расчет объема/контента просто. о-первых, рассчитывать количество области цилиндра (то есть площадь круга), а затем умножив высоту.
Расчет цилиндра онлайн
Калькулятор окружности цилиндра или вычисление площади или поверхности цилиндра, содержание или объем цилиндра, узор валков площадь или длина окружности оболочки или содержимого. Расчет объема войны онлайн. Формула для вычисления цилиндра.
Ссылки
Как рассчитать …
Выделенные жирным шрифтом ссылки уже работают. Другие пока содержат только лишь формулу.Могло бы вас заинтересовать
Калькулятор расчёта объёмов и площадей поверхности тел
Назначение калькулятора
Калькулятор позволяет рассчитать объёмы и площади поверхности таких геометрических тел, как конус, усечённый конус, шар и цилиндр.
В работе калькулятора используются следующие формулы:
1. Конус
1.1 Объём конуса
Для расчёта объёма конуса применяется формула:
h – высота конуса;
Sосн – площадь основания, которое представляет собой круг, соответственно его площадь может быть рассчитана по формуле:
R – радиус основания;
d – диаметр основания.
Тогда итоговая формула будет иметь вид:
1.2 Площадь поверхности конуса
Площадь боковой поверхности конуса может быть вычислена по формуле:
R – радиус основания;
L – образующая конуса;
Образующую можно выразить через радиус и высоту h:
Тогда формула площади боковой поверхности примет вид:
Или через диаметр:
Чтобы вычислить полную площадь поверхности, необходимо к площади боковой поверхности добавить площадь основания конуса:
2. Цилиндр
2.1 Объём цилиндра
Объём цилиндра может быть вычислен по следующей формуле:
h – высота цилиндра;
Sосн> – площадь основания, которое представляет собой круг, соответственно его площадь может быть рассчитана по формуле:
Тогда итоговая формула будет иметь вид:
2.
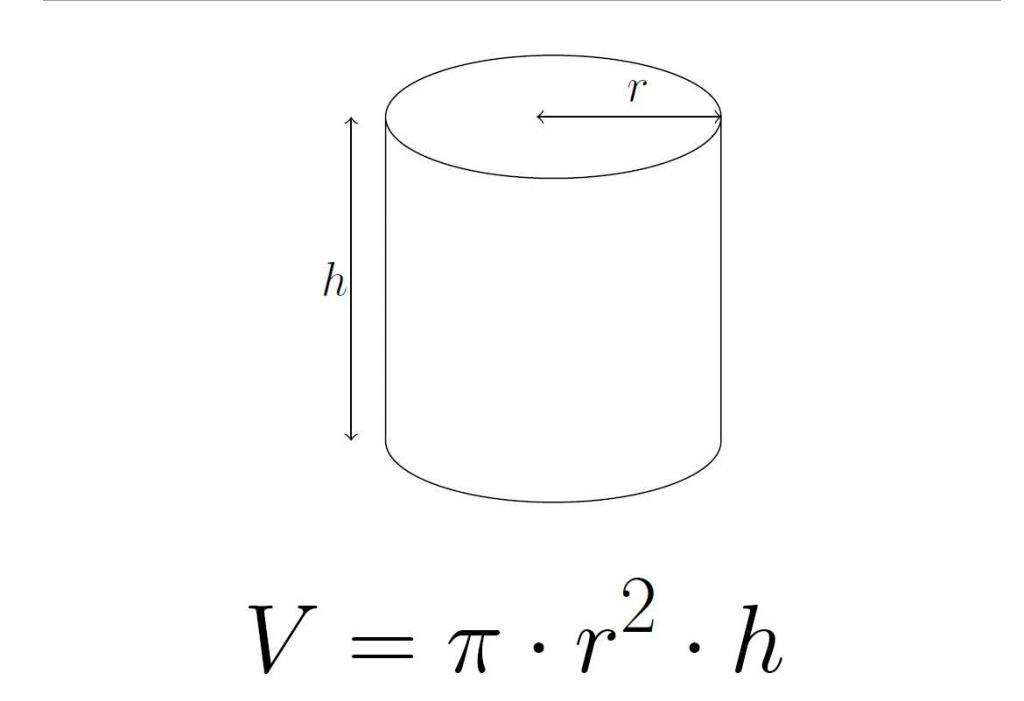 2 Площадь поверхности цилиндра
2 Площадь поверхности цилиндраПлощадь боковой поверхности цилиндра находится по формуле:
d – диаметр цилиндра;
h – высота цилиндра;
Для того, чтобы найти площадь полной поверхности цилиндра необходимо к площади боковой поверхности добавить две площади основания:
3. Шар (сфера)
3.1 Объём шара вычисляется по формуле:
R – радиус шара;
Если радиус выразить через диаметр, то получим следующее:
3.2 Площадь поверхности шара вычисляется по формуле:
Через диаметр:
4. Усечённый конус
4.1 Объём усечённого конуса рассчитывается по формуле:
R – радиус нижнего основания;
r – радиус верхнего основания;
h – высота конуса;
4.2 Площадь боковой поверхности усечённого конуса находится по формуле:
L – образующая усечённого конуса;
Если образующую выразить через высоту, то получим следующее:
Для того, чтобы вычислить площадь полной поверхности усечённого конуса необходимо к площади боковой поверхности добавить площади верхнего и нижнего основания:
Вычислитель объема и площади цилиндра
Как найти объем и площадь цилиндра?
Цилиндр — это трехмерное твердое тело с конгруэнтными основаниями в паре параллельных плоскостей. Эти основания представляют собой конгруэнтные круги. Ось цилиндра — это отрезок прямой с концами в центрах оснований.
Высота или высота цилиндра, обозначаемая $ h $, представляет собой перпендикулярное расстояние между его круглыми основаниями. Существует два типа цилиндров:
- Правый цилиндр;
- Наклонный цилиндр.
Работа с объемом цилиндра и площадью поверхности с шагом показывает полный пошаговый расчет для определения площади поверхности и объема цилиндра с длиной его базового радиуса $ 5 \; in $ и высотой $ 10 \; in $ по формулам площади поверхности и объема. Для любые другие значения для длины базового радиуса и высоты цилиндра, просто введите два положительных действительных числа и нажмите кнопку «Создать работу». кнопка. Учащиеся начальной школы могут использовать этот калькулятор цилиндров для создания работы, проверки результатов площади поверхности и объема трехмерных тел или для эффективного выполнения домашних заданий.
▷ Калькулятор объема цилиндра 📐
Быстрая навигация:
- Формула объема цилиндра
- Как рассчитать объем цилиндра?
- Пример: найти объем цилиндра
- Практическое применение
Формула для объема цилиндра: высота x π x (диаметр / 2) 2 , где (диаметр / 2) — радиус основания (d = 2 xr), поэтому можно записать это иначе равно высота x π x радиус 2 .Изображение на рисунке ниже:
Сначала измерьте диаметр основания (обычно это проще, чем измерять радиус), затем измерьте высоту цилиндра. Для правильного расчета у вас должны быть два измерения в одинаковых единицах длины. Результат вычисления объема цилиндра всегда выражается в кубических единицах в зависимости от входной единицы: в 3 , фут 3 , ярд 3 , см 3 , м 3 , км 3 , и так далее.
Как рассчитать объем цилиндра?Цилиндр можно представить как набор окружностей, наложенных друг на друга. Высота цилиндра дает нам глубину укладки, а площадь основания дает нам площадь каждого круглого среза. Умножение площади среза на глубину стопки — простой способ концептуализировать способ вычисления объема цилиндра. Поскольку на практике легче измерить диаметр (трубы, круглого стального прутка, кабеля и т. Д.).), чем для измерения радиуса, и в большинстве технических схем задается именно диаметр, наш калькулятор объема цилиндра принимает диаметр в качестве входных данных. Если вместо этого у вас есть радиус, просто умножьте его на два.
Использование формулы и выполнение вычислений вручную может быть затруднено из-за значения константы π: ~ 3,14159, с которой может быть сложно работать, поэтому вычислитель объема цилиндра значительно упрощает задачу.
Пример: найти объем цилиндра
Применять формулы объема легко, если известна высота цилиндра и задано одно из следующих значений: радиус, диаметр или площадь основания.Например, если заданы высота и площадь 5 футов и 20 квадратных футов, объем — это просто произведение двух: 5 x 20 = 100 кубических футов.
Если указан радиус, то с помощью второго уравнения выше можно получить объем цилиндра с несколькими дополнительными шагами. Например, высота 10 дюймов, а радиус 2 дюйма. Сначала мы находим площадь на 3,14159 x 2 2 = 3,14159 x 4 = 12,574, затем умножаем это на 10, чтобы получить объем 125,74 кубических дюйма. Использование более высокого уровня точности для π приводит к более точным результатам, например.г. наш калькулятор вычисляет объем этого цилиндра как 125,6637 куб. дюймов
Практическое применениеЦилиндр — одна из наиболее широко используемых форм кузова в машиностроении и архитектуре: от туннелей, крытых проходов до труб, кабелей, круглых стержней, цилиндров и поршней в двигателе вашего автомобиля — цилиндры везде. Расчет объема цилиндра полезен, когда вы хотите узнать его объем или количество жидкости или газа, которое вам нужно заполнить, например сколько воды нужно для заполнения джакузи.Цилиндрические аквариумы также довольно распространены, как и цилиндрические искусственные озера, фонтаны, газовые баллоны / резервуары и т. Д.
Объем цилиндра с калькулятором
Объем цилиндра с калькулятором — Math Open ReferenceОпределение: Количество кубических единиц, которое точно заполнит цилиндр.
Попробуй это Перетащите оранжевую точку, чтобы изменить размер цилиндра. Объем рассчитывается при перетаскивании.
Как найти объем цилиндра
Хотя цилиндр технически не является призмой, он обладает многими свойствами призмы.Как призмы, объем находится путем умножения площади одного конца цилиндра (основания) на его высоту.
Поскольку конец (основание) цилиндра представляет собой круг, площадь этого круга определяется формулой:
Умножая на высоту х получаем где:
π — Pi, приблизительно 3,142
r — радиус круглого конца цилиндра
h высота цилиндра
Калькулятор
Используйте калькулятор выше, чтобы рассчитать высоту, радиус или объем цилиндра.
Введите любые два значения, и будет вычислено недостающее. Например: введите радиус и высоту и нажмите «Рассчитать». Объем будет рассчитан.
Аналогичным образом, если вы введете высоту и объем, будет рассчитан радиус, необходимый для получения этого объема.
Объем частично заполненного баллона
Одно из практических применений — это горизонтальный цилиндрический резервуар, частично заполненный жидкостью. Используя приведенную выше формулу, вы можете найти объем цилиндра, обеспечивающий его максимальную вместимость, но вам часто нужно знать объем жидкости в резервуаре с учетом глубины жидкости.
Это можно сделать, используя методы, описанные в Объем горизонтального цилиндрического сегмента.
Наклонные цилиндры
Напомним, что наклонный цилиндр это тот, который «наклоняется» — где верхний центр не находится над базовой центральной точкой. На рисунке выше отметьте «разрешить наклон» и перетащите верхнюю оранжевую точку в сторону, чтобы увидеть наклонный цилиндр.
Оказывается, для них формула объема работает одинаково. Однако в формуле необходимо использовать перпендикулярную высоту.Это вертикальная линия слева на рисунке выше. Чтобы проиллюстрировать это, отметьте «Высота фиксации». Когда вы перетаскиваете верхнюю часть цилиндра влево и вправо, наблюдайте за вычислением объема и обратите внимание, что объем никогда не изменяется.
См. Наклонные цилиндры для более глубокого обсуждения того, почему это так.
Шт.
Помните, что радиус и высота должны быть в одних и тех же единицах — при необходимости преобразуйте их. Результирующий объем будет в этих кубических единицах. Так, например, если высота и радиус указаны в сантиметрах, то объем будет в кубических сантиметрах.Что стоит попробовать
- На рисунке выше нажмите «сбросить» и «скрыть детали».
- Перетащите две точки, чтобы изменить размер и форму цилиндра.
- Рассчитать объем этого цилиндра
- Щелкните «Показать подробности», чтобы проверить свой ответ.
Связанные темы
(C) Открытый справочник по математике, 2011 г.
Все права защищены.
Калькулятор объема цилиндра
Рассчитайте объем цилиндра, включая его площадь поверхности и сколько жидкости он может вместить.
Информация о калькуляторе объема цилиндра…
Для расчета введите высоту цилиндра, измеренную сверху вниз; И радиус цилиндра, равный половине диаметра.
Если вы рассчитываете форму усеченного конуса, например чашки или кашпо, используйте Калькулятор объема конической створки.
Расчет площади поверхности цилиндра
Площадь поверхности рассчитывается путем сложения всех внешних сторон цилиндра.
Вы можете использовать площадь поверхности в качестве отправной точки для приблизительного определения того, как много глазури, которую может использовать ваше изделие. Например, если вы сделали цилиндрический сосуд, открыт сверху, и остекляют всю деталь, кроме внешней нижней части, которая находится на полки печи, вы можете удвоить площадь поверхности (при условии, что вы также остеклите внутри) и вычесть нижний один раз, а верхний два раза, поскольку его нет.
Формула для расчета площади поверхности цилиндра:
Площадь = 2 * π * r 2 + 2 * π * r * h
, где r — радиус, h — высота, а π (pi) приблизительно равно 3.14.
Расчет объема цилиндра
Объем — это то, сколько жидкости может вместить кусок. Например, если это керамическая кружка или чашка — это количество кофе, чая или другой жидкости, которое она может вместить. Формула для расчета объема цилиндра:
Объем = πr 2 ч
, где r — радиус, h — высота, а π (pi) приблизительно равно 3,14
Результат вычисления объема цилиндра выражается в кубических дюймах (или сантиметрах).С использованием объем, емкость цилиндра по жидкости рассчитывается в нескольких общих показателях (чашки, унции, миллилитры и др.)
Обратите внимание, что объем жидкости будет немного больше, чем он может вместить, если вы не измеряете с внутренних стенок баллона; В противном случае в расчет включается толщина стены.
Калькулятор объема цилиндра— примеры, факты
Вычислитель объема цилиндра рассчитывает объем жидкости / воздуха / любого другого вещества, которое должно быть перенесено в этот цилиндр.Для этого калькулятор использует высоту и радиус цилиндра.
Цилиндр выглядит как банка из-под кокса, круглый резервуар для воды и т. Д. Каждый из них несет жидкость, воздух или любое другое вещество. Чтобы рассчитать количество того, что должно храниться в этом цилиндре, нам нужно знать объем цилиндра.
Что такое калькулятор объема цилиндра?
Калькулятор объема цилиндра — это онлайн-инструмент, используемый для расчета объема цилиндра. Это помогает рассчитать объем при заданном радиусе и высоте за несколько секунд.Чтобы использовать этот калькулятор объема цилиндра , введите значения в поля ввода, приведенные ниже.
Вычислитель объема цилиндра
* используйте только 3 цифры.
Как пользоваться калькулятором объема цилиндра?
Чтобы использовать вычислитель объема цилиндра, выполните следующие действия:
- Шаг 1: Зайдите в онлайн-калькулятор объема цилиндра Cuemath.
- Шаг 2: Введите значения радиуса и высоты в поле ввода.
- Шаг 3: Нажмите кнопку «Рассчитать», чтобы найти объем цилиндра.
- Шаг 4: Нажмите кнопку «Сброс», чтобы очистить поля и ввести новые значения.
Как работает калькулятор объема цилиндра?
Объем цилиндра — это вместимость цилиндра или мера занимаемого им пространства. Он рассчитывается по формуле πr 2 h, где r — радиус круглого основания, h — высота цилиндра, а π (Pi) — математическая константа с приблизительным значением 3.14. Значения радиуса и высоты помещаются в формулу для получения объема цилиндра.
Хотите найти сложные математические решения за секунды?
Воспользуйтесь нашим бесплатным онлайн-калькулятором для решения сложных вопросов. Cuemath находит решения простым и легким способом.
Забронируйте бесплатную пробную версию Класс
Объем цилиндров Примеры
Пример 1: Цилиндр имеет радиус 3 единицы и высоту 5 единиц.Найдите объем цилиндра и проверьте его с помощью калькулятора объема цилиндра.
Решение:
Формула, по которой определяется объем цилиндра = πr 2 ч. Радиус = 3 единицы, высота = 5 единиц. Итак, подставим значения:
Объем цилиндра = πr 2 ч
= 3,14 × 3 × 3 × 5 = 141,3 единиц
Следовательно, Объем цилиндра = 141,3 шт.
Пример 2: Объем коксовой банки составляет 150 единиц с радиусом 2.5 шт. Найдите высоту банки из-под кокса.
Решение:
Формула, по которой определяется объем цилиндра = πr 2 ч. Объем составляет 150 единиц, а радиус — 2,5 единицы, т.е. диаметр = 5 единиц.
Объем цилиндра = πr 2 ч
150 = 3,14 × 2,5 × 2,5 × в = 150 / 19,625
= 7,643 единиц
Следовательно, высота цилиндра 7,643 единицы.
Точно так же вы можете попробовать вычислить объем цилиндра, чтобы найти объем со следующими размерами:
- Найдите объем цилиндра с радиусом 7 единиц и высотой 14 единиц.
- Найдите объем цилиндра, радиус которого 24 единицы, а высота 345 единиц.
☛ Также проверьте:
Калькулятор объема цилиндра| Математические онлайн-калькуляторы с пояснениями o
Введите радиус и высоту основания цилиндра, чтобы рассчитать объем цилиндра.
★ ★ ★ ★ ★ [3 голосов]
Что такое цилиндр?
цилиндр — это трехмерный твердый объект, имеющий 2 параллельных основания, которые представляют собой конгруэнтные окружности одинакового диаметра
Объем цилиндра рассчитывается по следующему уравнению:
- Основание x высота (основание равно пи r 2 , которое является уравнением для объема круга.r — радиус, который представляет собой расстояние от центра круга до его внешнего края)
Примечание: Не забудьте использовать одну и ту же единицу измерения для каждого измерения при вычислении объема объекта.
Объем твердых объектов измеряется в:
- кубических футов
- кубических метров
- кубических ярдов
Объем жидкостей измеряется в:
- литров
- квартах
- пинт 120009 галлонов
- Калькулятор объема куба — куб — это трехмерный твердый объект, ограниченный шестью квадратными гранями, гранями или сторонами, по три пересечения в каждой вершине.
- Калькулятор объема конуса — конус — это трехмерная геометрическая форма, которая плавно сужается от основания (обычно плоского и круглого) к точке, называемой вершиной или вершиной.
- Калькулятор объема цилиндра цилиндр — это трехмерный твердый объект, имеющий 2 параллельных основания, которые представляют собой конгруэнтные окружности одинакового диаметра.
- Калькулятор объема прямоугольной призмы — прямоугольник — это любой четырехугольник с четырьмя прямыми углами. Призма имеет одинаковое поперечное сечение по всей длине.
- Калькулятор объема неправильной призмы. — Призма имеет одинаковое поперечное сечение по всей длине. Неправильная форма — это форма, которая не соответствует стандартным определенным и повторяемым математическим правилам.
- Калькулятор объема пирамиды — пирамида представляет собой многогранник [трехмерный твердый объект], образованный путем соединения многоугольного основания и точки, называемой вершина.
- Калькулятор объема сферы — сфера — это трехмерный твердый объект идеально круглой формы.
- Калькулятор объема эллипсоида — Эллипсоид — это трехмерный твердый объект с замкнутой квадратичной поверхностью, который является трехмерным аналогом эллипса
- Площадь поверхности цилиндра должна быть обозначена как квадрат
- Объем баллона должен быть обозначен в кубических единицах
- Форму окончательного ответа можно либо оставить с точным числом «Пи», либо использовать клавишу «Пи» на калькуляторе для десятичного приближения.Для реальных приложений нам нужен десятичный ответ. Спросите учителя о округлении десятичной дроби и не забывайте о метке.
Онлайн-калькулятор цилиндра ниже автоматически рассчитает объем цилиндра на основе введенных вами измерений.
У вас также будет промежуточная сумма, которая будет накапливаться по мере ввода новых измерений в калькулятор объема.
Математика Калькуляторы объема
Математические калькуляторы
Вам также могут пригодиться следующие математические калькуляторы.
Калькулятор объема цилиндра | Найти объем цилиндра
Введение в цилиндры «Примеры из реальной жизни»
Цилиндры — одна из наиболее часто используемых форм.Если вы сейчас пьете чашку чая, вы держите цилиндр. Все, с чем мы сталкиваемся в повседневной жизни, в основном имеет цилиндрическую форму. Как и консервы в вашей кладовой — это цилиндры.
Формы цилиндров могут варьироваться от высоких до узких, форм-фактор зависит от того, для каких целей он будет использоваться. Но всегда помните, что в случае цилиндров основания всегда будут параллельны, так как здесь используется формула объема цилиндра.
Если вы когда-нибудь «развернете» цилиндр, вы обнаружите, что сторона цилиндра представляет собой прямоугольник.Если вы не знакомы с длиной прямоугольника, воспользуйтесь калькулятором площади прямоугольника.
Типы цилиндров «Правый и наклонный цилиндры»
Существует два наиболее часто обсуждаемых типа цилиндров по геометрии: правый и наклонный цилиндры. Давайте рассмотрим оба по порядку.
Правые цилиндры: Если вы обнаружите, что два основания расположены точно друг над другом без какого-либо отклонения, а ось расположена под прямым углом к основанию, это называется правыми цилиндрами. Правые цилиндры в большинстве случаев имеют прямой форм-фактор с идеальным углом оси в основании или центре.
Правый цилиндр
Наклонные цилиндры: В случае наклонных цилиндров одна сторона основания цилиндра смещена вбок. Ось параллельна, но не вправо по отношению к углам оснований. Именно поэтому его называют наклонными цилиндрами.
Наклонный цилиндр
Как найти площадь поверхности и как найти объем цилиндра? Связь цилиндра с призмой
Цилиндрыпохожи на призму тем, что оба имеют два основания, верхнее и нижнее, которые могут быть наклонными и правыми.Так что, если вы уже знаете формулы призмы для площади поверхности и объема призмы, то объем цилиндра легко понять.
Формулы для площади поверхности и объема цилиндра имеют формат, аналогичный формулам для призм. Но в отличие от призм, которые имеют так много боковых граней из-за их многоугольной природы для оснований, цилиндры имеют только одну боковую поверхность из-за их окружностей для оснований.
Поскольку объемные цилиндры и призмы очень похожи, мы можем сначала использовать ту же формулу для площади поверхности.Если вы хотите получить среднее значение чисел перед расчетом, используйте для этой цели Калькулятор среднего значения.
Формула площади поверхности цилиндров:
SA = 2B + LA
, где SA относится к площади поверхности, B относится к ПЛОЩАДИ основания, а LA относится к боковой области.
До тех пор, пока вы знаете формулы для длины окружности и площади круга, вы можете продолжать работать с исходной формулой с заменой без необходимости запоминать что-либо еще.
Не забудьте сказать формулу словами и подставить то, что вы говорите, в формулу объема цилиндра. Площадь поверхности цилиндра равна удвоенной площади основания плюс площадь боковой поверхности цилиндра.
Поскольку основание — круг, а боковая поверхность — прямоугольник, формула меняется на
SA = 2 (pi r 2 ) + (2pi r) h
Примечание: не стоит запоминать эту формулу. Его воссоздание займет всего несколько секунд.То же самое и с формулой объема.
Формула объема цилиндров:
A = Bh
где A — площадь, B — площадь основания, а «h» — высота цилиндра. Запомните эту формулу, а затем подставьте соответствующие формулы в кружок. Результат
A = (pi r 2 ) ч
Высота цилиндра: Перпендикулярное расстояние между основаниями цилиндра называется высотой и обозначается буквой «h».
Радиус цилиндра: Радиус основания называется радиусом цилиндра и обозначается словом «r».
Ось цилиндра: А-линия, соединяющая центр каждой стороны цилиндра, называется осью. Чтобы найти номер градиента, который определяет крутизну и направление линии, используйте Калькулятор уклона.
Что следует помнить при расчете площади поверхности и объема цилиндров
Калькулятор объема цилиндра
Мы можем утверждать, что вычисление объема цилиндра представляет собой значительную трудность для большинства людей, особенно молодых людей и студентов, и становится только хуже для нескольких значений и чисел.
Итак, если вы человек, который до сих пор не может найти правильное решение для расчета объема цилиндра для сложных задач.Тогда калькулятор объема цилиндра станет для вас благословением. Это один из самых простых в использовании калькулятор объема цилиндра, который вы можете найти в Интернете.
Простая конструкция нашего калькулятора цилиндров с понятным пользовательским интерфейсом позволяет каждому легко управлять нашим калькулятором объема цилиндра без каких-либо проблем.
Наш калькулятор объема цилиндра превосходит любой другой калькулятор объема цилиндра с точки зрения надежности и результатов.
Мы используем новейшие подходы для повышения производительности калькулятора объема цилиндра, чтобы он мог дать вам объем цилиндра в течение нескольких секунд после ввода значений.
Как пользоваться нашим калькулятором объема цилиндра?
Если вы когда-либо использовали стандартный калькулятор для каких-либо целей, то калькулятор объема цилиндра для вас так же прост, как и использование любого другого стандартного калькулятора.
Вам нужно только ввести значение радиуса «r» и высоты «h» в соответствующие поля соответственно, и все готово для определения объема цилиндра с помощью нашего калькулятора объема цилиндра.
Кроме того, нашим калькулятором объема цилиндров можно пользоваться абсолютно бесплатно, без каких-либо подписок или скрытых платежей.
Применение цилиндров «в реальной жизни»
Как выясняется, все цилиндры имеют трехмерные фигуры. Итак, наиболее распространенное использование цилиндров в реальной жизни — это упаковка из материала, металла или картона, необходимого для изготовления цилиндра.



 Поэтому формулу объема цилиндра можно записать через площадь основания и высоту:
Поэтому формулу объема цилиндра можно записать через площадь основания и высоту: 14156 ⋅ 1.25 ≈ 3.927 см3
14156 ⋅ 1.25 ≈ 3.927 см3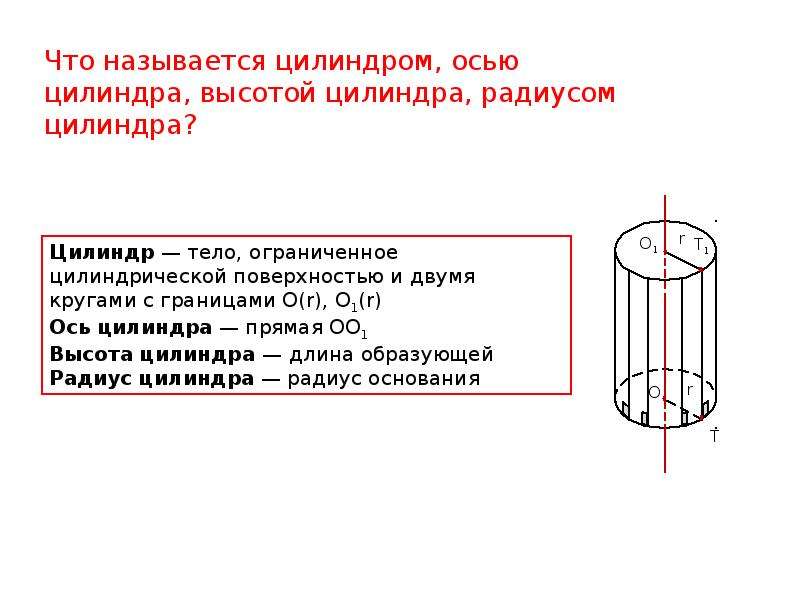 Также, цилиндр представляет собой тело, ограниченное цилиндрической поверхностью и двумя параллельными плоскостями, пересекающими ее. Эта поверхность образуется при движении прямой параллельно самой себе. При этом выделенная точка прямой перемещается вдоль определенной плоской кривой (направляющая). Данная прямая называется образующей цилиндрической поверхности.
Также, цилиндр представляет собой тело, ограниченное цилиндрической поверхностью и двумя параллельными плоскостями, пересекающими ее. Эта поверхность образуется при движении прямой параллельно самой себе. При этом выделенная точка прямой перемещается вдоль определенной плоской кривой (направляющая). Данная прямая называется образующей цилиндрической поверхности.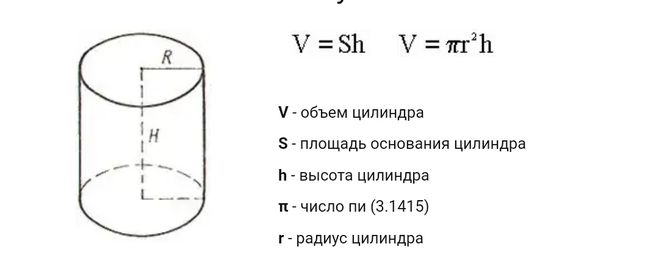


 ru/docs/poleznaya_inform/kak_rasschitat_obem_korobki_v_m3_i_litrakh/
ru/docs/poleznaya_inform/kak_rasschitat_obem_korobki_v_m3_i_litrakh/