Как вычислить площадь зная периметр сложной фигуры: Как найти площадь, зная периметр. Что такое периметр и площадь.

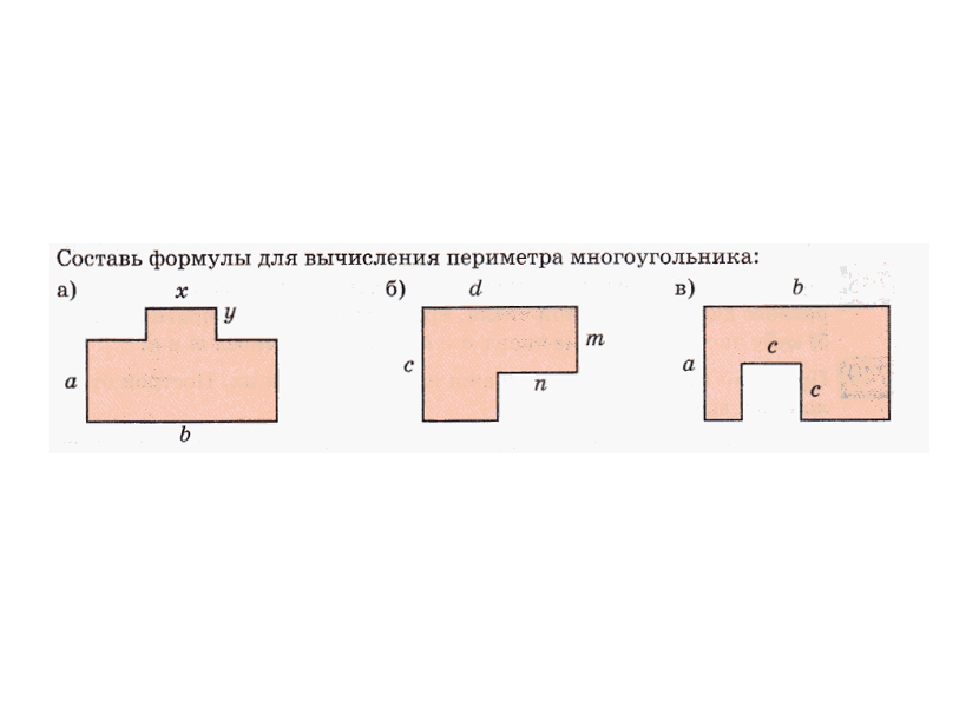
Как найти периметр сложной фигуры. Умение применять знания в нахождении периметра и площади геометрических фигур. Как найти периметр прямоугольника – онлайн-ресурсы

Построение урока:

1. Организация и мотивация учащихся к деятельности на уроке.
2. Организация восприятия нового материала на основе наглядного материала
3. Организация осмысления.
4. Первичная проверка понимания нового материала.
5. Организация первичного закрепления и самостоятельный анализ учебной информации.
6. Применение полученных знаний на практикуме.

Цели урока:

1. Обучающая. Обеспечить усвоение учащимися нахождения площади и периметра геометрических фигур;

визуального восприятия материала на уроке; осмыслено понимать, что такое площадь и периметр.

2. Развивающая. Использовать на уроке развивающие упражнения, активизировать

мыслительную деятельность школьников.

3. Воспитательная. Обеспечить развитие ценностно-смысловой культуры учащихся;

мотивации на умение правильно достигать поставленной цели —

совпадение ожидания и результата.

Оборудование:

1. М.И.Моро и др. “Математика” — учебник для 3 класса начальной школы, 1 часть.
2. Рабочая тетрадь по математике.
3. Ручка, линейка, простой карандаш, треугольник, ножницы.
4. Модели геометрических фигур для нахождения площади.
5. Над доской плакаты с формулами нахождения площади и периметра.

Средства обучения:

1. Дидактический материал.
2. Наглядные пособия.

Приемы обучения:

1. Сравнение предметов.
2. Сопоставления способов нахождения площади одной и той же фигуры.

Ход урока.

1. Организационный момент и сообщение темы урока.

Учитель: Здравствуйте, ребята. Сегодня мы продолжим изучение большой темы под названием “Площадь и периметр”. Тема нашего урока сегодня:“Умение применять знания в нахождении периметра и площади сложной фигуры”. Сложная фигура – это геометрическая фигура, состоящая из нескольких простейших фигур. Сначала, повторим то, что мы с вами изучили на прошлых уроках.

II. Устный счет.

Задачи на развитие.

Учитель: Найдите площадь данной фигуры, если сторона квадрата 1 см.

Фигура изображена на доске.

Ученик: Если 1 квадрат имеет площадь 1 см 2 , а квадратов изображено 5, то площадь этой фигуры равна 5 см 2 .

Учитель: Правильно. Следующее задание. Уберите 3 палочки, чтобы осталось 3 таких квадрата.

Ученик выходит к доске и убирает 3 палочки.

Учитель: Уберите 4 палочки, чтобы осталось 3 таких же квадрата.

Ученик выходит к доске и убирает 4 палочки. Решение.

III. Работа по теме урока

Учитель: Какие геометрические фигуры вы уже знаете?

Ученик: Прямоугольник.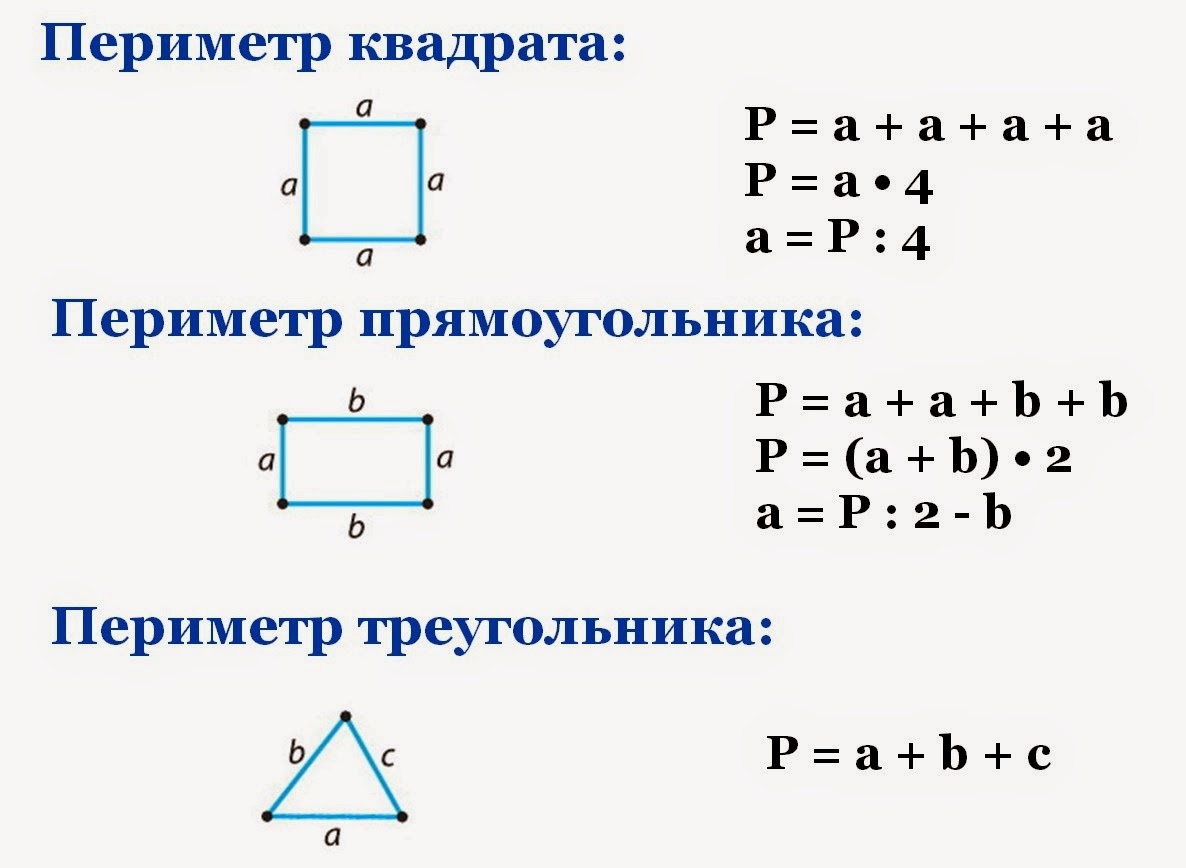

Ученик: Квадрат.

Учитель: Правильно. Что мы знаем о квадрате?

Ученик: У квадрата 4 стороны и 4 угла.

Учитель: Правильно. Каким свойством обладают стороны квадрата?

Ученик: Они равны.

Учитель: Правильно. А какие углы у квадрата?

Ученик: Они прямые.

Учитель: С помощью чего мы можем построить прямой угол?

Ученик: С помощью треугольника.

Учитель: Давайте построим квадрат со стороной 4 см в вашей тетради. С помощью каких инструментов мы будем чертить квадрат?

Ученик: С помощью линейки, карандаша и треугольника.

Ученики в тетрадях строят квадрат и раскрашивают его.

Учитель: Эта геометрическая фигура. Как найти периметр и площадь этого квадрата?

Ученик: Периметр – это сумма всех его сторон. Сторон у квадрата 4. Значит, 4 сложим 4 раза.

Учитель: Как это записать?

Ученики делают запись в тетради: “Найти площадь фигуры F1”.

Ученика вызывают к доске, и он пишет: Р = 4 + 4 + 4 + 4 = 16 (см)

Ученики делают запись в тетради.

Учитель: В каких единицах еще измеряется периметр?

Ученик: В сантиметрах, в миллиметрах, в метрах, в дециметрах, в километрах.

Учитель: Молодец! Как еще можно записать периметр?

Ученик: С помощью умножения.

Ученик записывает на доске: Р = 4 · 4 = 16 (см)

Ученики записывают в тетради.

Учитель: А чему равна площадь квадрата?

Ученик: Длину квадрата умножаем на его ширину. Так как стороны у квадрата равны, то

S = 4 · 4 = 16 (см 2)

Ученики делают запись в тетрадке и записывают — “Ответ: S = 16 см 2 ”.

Учитель: Какие еще единицы измерения площади вы знаете?

Ученик: квадратный сантиметр, квадратный дециметр, квадратный метр, квадратный миллиметр.

Учитель: А теперь усложним задачу. Перед вами лежит карточка.

На этой карточке изображен квадрат такой же, что и у вас в тетрадке. В середине этого квадрата — еще один квадрат со стороной 2 см. Сейчас вы возьмете ножницы и вырежете аккуратно этот маленький квадрат.

Ученики выполняют эту работу и делают запись в тетрадке: “Найти площадь фигуры F2”.

Учитель: У нас получилась фигура “с окошком” — F2. Как можно найти площадь этой интересной фигуры? Площадь квадрата уже известна и равна 16 см 2 .

Ученик: Нужно найти площадь маленького квадратика со стороной 2 см.

Ученик выходит к доске и записывает – S2 = 2 · 2 = 4 (см 2)

Ученики делают запись в тетрадке

Ученик: Из площади большого квадратика вычесть площадь маленького.

Учитель: Правильно.

Ученик записывает на доске – S = S1 – S2 = 16 – 4 = 12 (см 2)

Ученики делают запись в тетрадке.

Учитель: Внимательно посмотрите на эту фигурку и скажите, как еще можно измерить площадь? Можно ли эту фигуру как-то разрезать, чтобы получить фигуры, уже знакомые вам?

Ученики думают и говорят разные варианты.

Один из вариантов оказался очень интересным.

Ученик: Можно так разрезать, чтобы получились прямоугольники и показывает на доске, как это можно сделать.

Ученики разрезают фигуру, как показано на доске.

Учитель: А как находится площадь прямоугольника?

Ученик: Нужно длину умножить на ширину.

Учитель: У вас получилось четыре фигуры. Что можно сказать про них?

Ученик: Две фигурки, как близнецы – одинаковые, и вторые две – тоже одинаковые.

Можно найти площадь одной фигуры и умножить на 2.

Ученик решает на доске: S1 = 1 · 4 = 4 (см 2)

S2 = 1 · 2 = 2 (см 2)

S = 2 · S1 + 2 · S2 = 2 · 4 + 2 · 2 = 8 + 4 = 12(см 2)

Учитель: Молодец! У нас получилась то же значение площади, что и раньше.

Ученики пишут в тетрадке – “Ответ: S = 12 см 2 .”

Учитель: Вы, наверное, устали?

Настало время отдыхать.

Предлагаю усталость

Физкультминуткой снять.

IV. Физкультминутка.

Каждый день по утрам
Делаем зарядку (ходьба на месте).
Очень нравится нам делать по порядку:
Весело шагать (ходьба),
Руки поднимать (руки вверх),

Приседать и вставать (приседание 4-6 раз),
Прыгать и скакать (10 прыжков).

Учитель: А теперь сели за парты и

посмотрите на следующую модель. Фигура F3

Как найти площадь этой интересной фигуры?

Ученик: Треугольник, который выступает

можно отрезать и подставить в ту часть, где

треугольник “уходит” внутрь.

Учитель: Давайте возьмем ножницы, отрежем треугольник и подставим в верхнюю часть.

Что за фигура у нас получилась?

Ученик: Прямоугольник!

Учитель: Как найти площадь этого прямоугольника,

Если стороны нам неизвестны.

Ученик: Мы можем взять линейку и измерить

длину и ширину прямоугольника.

Ученики делают запись – “Найти площадь фигуры F3”.

Ученики линейкой измеряют длину и ширину. Получается длина, а = 6 см, ширина в = 2 см.

Ученик: Площадь данной фигуры равна S = 6 · 2 = 12 (см 2).

Ученики делают запись в тетрадке и записывают – “Ответ: S = 12 см 2 .

Учитель: Но это еще не все. Перед вами следующая фигура. Необходимо найти ее площадь.

Что за фигура перед вами?

Ученик: Треугольник. Но площадь треугольника

мы не умеем находить!

Учитель: Это правда. Из этого треугольника

сделаем прямоугольник. Я вам подскажу. Фигура F4

Сначала мы этот треугольник сложим пополам

Ученики: Мы поняли! Правую

сторону переворачиваем.

Получится прямоугольник.

Ученик: С помощью линейки измеряем

длину а и ширину в, и по S = а· в,

находим площадь.

Учитель: Если мы при измерении, мы

получим, что длина

будет выражена в мм, а ширина в см,

что нам делать?

Ученик: Обязательно длину и ширину перевести в одну единицу измерения.

Ученики записывают в тетрадке: “Найти площадь фигуры F4”.

V. Работа в парах.

Учитель: А теперь я предлагаю поработать в паре. Вас за партой двое. Один ученик (I вариант) находит периметр данной фигуры, а второй (II вариант)- площадь.

Для этого начертим в тетради эту фигуру. После того, как вы выполните задание, поменяетесь тетрадями и проверите результаты друг у друга.

Ученики выполняют задание и результаты

записывают в тетрадь.

Учитель: Что у вас получилось?

Ученик: Квадрат со стороной 3 см. Р = 3 · 4 = 12(см)

S = 3 · 3 = 9 (см 2) 3 см

Ученики записывают: “Ответ: P = 12 см, S = 9 см 2 .

Учитель: Молодцы! А теперь я вам предлагаю поработать самостоятельно.

Найти площадь следующей фигуры. Она лежит перед вами.

VI. Самостоятельная работа по закреплению изученного материала.

Учитель раздает заранее заготовленные фигуры.

Ученики самостоятельно, без помощи учителя, разрезают эту фигуры, получают три прямоугольника.

Ученики делают запись: “ Найти площадь фигуры F5”.

Ученики находят S1 = 4 · 3 = 12(см 2), S2 = 2 · 1 = 2(см 2), потом находят площадь данной фигуры: S = S1 + S2 + S2 = 12 + 2 + 2 = 16 (см 2) и делают запись в тетради, затем

записывают: “Ответ: S = 16 см 2 ”.

Учитель: Понравился урок?

Ученики: Да.

Учитель: Что вы нового узнали на этом уроке?

Ученик: Мы научились находить площадь и периметр сложных фигур. Это оказалось очень просто. Нужно немного подумать и эту фигуру перестроить или переделать в ту, периметр и площадь, которой, мы уже умеем находить.

Учитель: Я очень рада, что вам понравилось. Дома еще раз повторить формулы нахождения периметра и площади квадрата и прямоугольника; вспомнить, как переводить одну единицу

в другую. Сегодня хорошо отвечали следующие ученики. . .

Учитель выставляет оценки.

VII. Домашнее задание: учебник стр. 77 № 8.

Знания о том, как найти периметр, учащиеся получают еще в начальной школе. Потом эта информация постоянно используется на протяжении всего курса математики и геометрии.

Общая для всех фигур теория

Стороны принято обозначать латинскими буквами. Причем их можно обозначать как отрезки. Тогда букв потребуется по две для каждой стороны и записанные большими. Или ввести обозначение одной буквой, которая обязательно будет маленькой.
Буквы всегда выбирают по алфавиту. Для треугольника они будут первыми тремя. У шестиугольника их будет 6 — от а до f. Это удобно для введения формул.

Теперь о том, как найти периметр. Он является суммой длин всех сторон фигуры. Количество слагаемых зависит от ее вида. Обозначается периметр латинской буквой Р. Единицы измерения совпадают с теми, которые даны для сторон.

Формулы периметров разных фигур

Для треугольника: Р=а+в+с.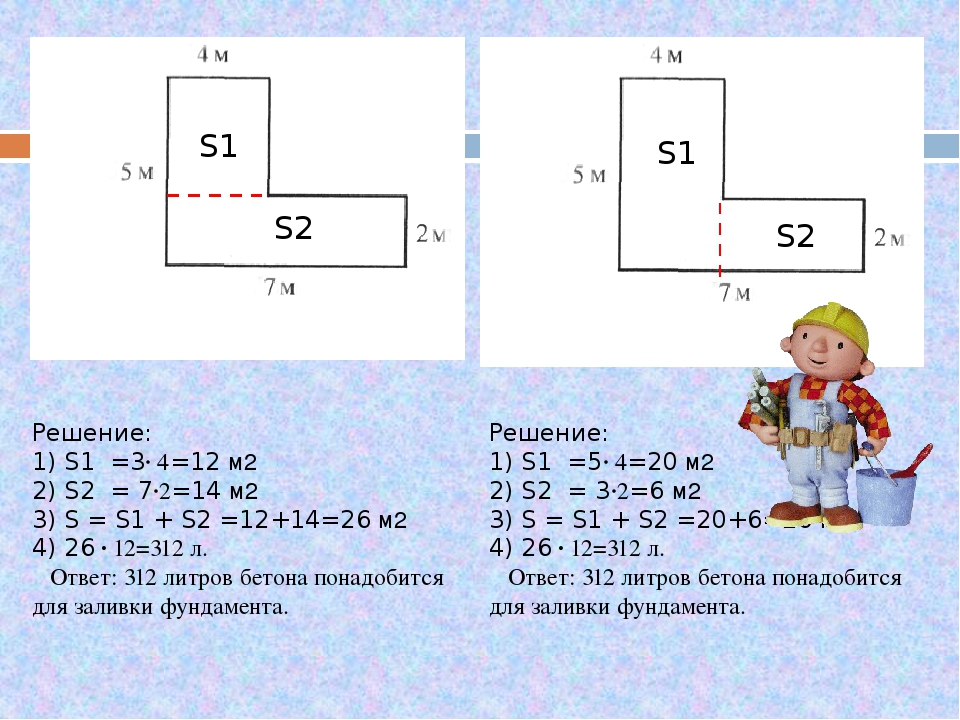 Если он равнобедренный, то формула преобразуется: Р=2а+в. Как найти периметр треугольника, если он равносторонний? Поможет такая: Р=3а.

Для произвольного четырехугольника: Р=а+в+с+d. Его частным случаем является квадрат, формула периметра: Р=4а. Есть еще прямоугольник, тогда требуется такое равенство: Р=2(а+в).

Как быть, если неизвестна длина одной или нескольких сторон треугольника?

Воспользоваться теоремой косинусов, если среди данных есть две стороны и угол между ними, который обозначается буквой А. Тогда до того, как найти периметр, придется посчитать третью сторону. Для этого пригодится такая формула: с² = а² + в² — 2 ав cos(А).

Частным случаем указанной теоремы является сформулированная Пифагором для прямоугольного треугольника. В ней значение косинуса прямого угла становится равным нулю, а значит, последнее слагаемое просто исчезает.

Бывают ситуации, когда узнать, как найти периметр треугольника, можно по одной стороне. Но при этом известны еще и углы фигуры. Здесь на помощь приходит теорема синусов, когда отношения длин сторон к синусам соответствующих противолежащих углов равны.

В ситуации, когда периметр фигуры нужно узнать по площади, пригодятся другие формулы. Например, если известен радиус вписанной окружности, то в вопросе о том, как находить периметр треугольника, пригодится следующая формула: S=р*r, здесь р — полупериметр. Его нужно вывести из данной формулы и умножить на два.

Примеры задач

Условие первой. Узнать периметр треугольника, стороны у которого 3, 4 и 5 см.
Решение. Нужно воспользоваться равенством, которое указано выше, и просто подставить в него данные в задаче значения. Расчеты легки, они приводят к числу 12 см.
Ответ. Периметр треугольника равен 12 см.

Условие второй. Одна сторона треугольника равна 10 см. Известно, что вторая на 2 см больше первой, а третья в 1,5 раза больше первой. Требуется вычислить его периметр.
Решение . Для того чтобы его узнать, потребуется сосчитать две стороны. Вторая определится как сумма 10 и 2, третья равна произведению 10 и 1,5. Потом останется только сосчитать сумму трех значений: 10, 12 и 15. Результатом будет 37 см.
Ответ. Периметр равняется 37 см.

Условие третьей. Имеются прямоугольник и квадрат. Одна сторона прямоугольника равна 4 см, а другая на 3 см больше. Нужно вычислить значение стороны квадрата, если его периметр меньше на 6 см, чем у прямоугольника.
Решение. Вторая сторона прямоугольника равна 7. Зная это, легко вычислить его периметр. Расчет дает 22 см.
Чтобы узнать сторону квадрата, нужно сначала вычесть 6 из периметра прямоугольника, а потом разделить полученное число на 4. В результате имеем число 4.
Ответ. Сторона квадрата 4 см.

В следующих тестовых заданиях требуется найти периметр фигуры, изображенной на рисунке.

Найти периметр фигуры можно разными способами. Можно преобразовать исходную фигуру таким образом, чтобы периметр новой фигуры можно было бы легко вычислить (например, перейти к прямоугольнику).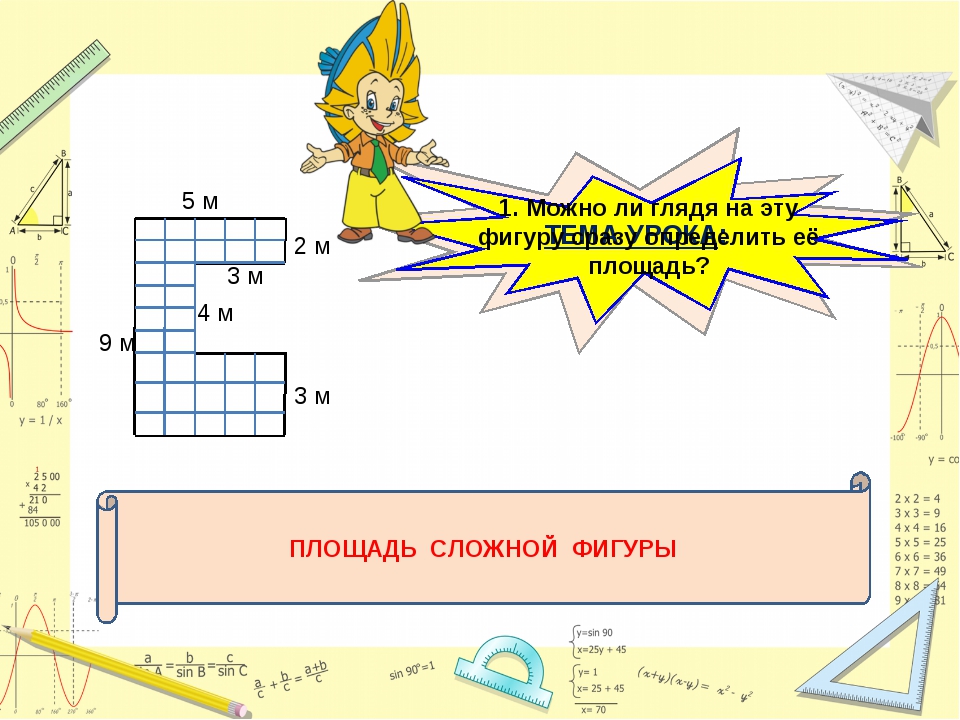

Другой вариант решения — искать периметр фигуры непосредственно (как сумму длин всех её сторон). Но в этом случае нельзя полагаться только на рисунок, а находить длины отрезков, исходя из данных задачи.

Хочу предупредить: в одном из заданий среди предложенных вариантов ответов я не нашла того, который получился у меня.

C) .

Перенесем стороны маленьких прямоугольников с внутренней области во внешнюю. В результате большой прямоугольник замкнулся. Формула для нахождения периметра прямоугольника

В данном случае, a=9a, b=3a+a=4a. Таким образом, P=2(9a+4a)=26a. К периметру большого прямоугольника прибавляем сумму длин четырех отрезков, каждый из которых равен 3a. В итоге, P=26a+4∙3a=38a .

C) .

После переноса внутренних сторон маленьких прямоугольников во внешнюю область, получаем большой прямоугольник, периметр которого равен P=2(10x+6x)=32x, и четыре отрезка, два — диной по x, два — по 2x.

Итого, P=32x+2∙2x+2∙x=38x .

?) .

Перенесем 6 горизонтальных «ступенек» из внутренней части во внешнюю. Периметр полученного большого прямоугольника равен P=2(6y+8y)=28y. Осталось найти сумму длин отрезков внутри прямоугольника 4y+6∙y=10y. Таким образом, периметр фигуры равен P=28y+10y=38y .

D) .

Перенесем вертикальные отрезки из внутренней области фигуры влево, во внешнюю область. Чтобы получить большой прямоугольник, перенесём одни из отрезков длиной 4x в нижний левый угол.

Периметр исходной фигуры найдём как сумму периметра этого большого прямоугольника и длин оставшихся внутри трёх отрезков P=2(10x+8x)+6x+4x+2x=48x .

E) .

Перенеся внутренние стороны маленьких прямоугольников во внешнюю область, получим большой квадрат. Его периметр равен P=4∙10x=40x. Чтобы получить периметр исходной фигуры, нужно у периметру квадрата прибавить сумму длин восьми отрезков, каждый длиной 3x. Итого, P=40x+8∙3x=64x .

B) .

Перенесём все горизонтальные «ступеньки» и вертикальные верхние отрезки во внешнюю область. Периметр полученного прямоугольника равен P=2(7y+4y)=22y. Чтобы найти периметр исходной фигуры, нужно к периметру прямоугольника прибавить сумму длин четырех отрезков, каждый длиной y: P=22y+4∙y=26y .

D) .

Перенесем из внутренней области во внешнюю все горизонтальные линии и передвинем две вертикальные внешние линии в левом и правом углах, соответственно, на z левее и правее. В результате получим большой прямоугольник, периметр которого равен P=2(11z+3z)=28z.

Периметр исходной фигуры равен сумме периметра большого прямоугольника и длин шести отрезков по z: P=28z+6∙z=34z .

B) .

Решение полностью аналогично решению предыдущего примера. После преобразования фигуры находим периметр большого прямоугольника:

P=2(5z+3z)=16z. К периметру прямоугольника прибавляем сумму длин оставшихся шести отрезков, каждый из которых равен z: P=16z+6∙z=22z .

Достаточно узнать длину всех ее сторон и найти их сумму. Периметром называется совокупная длина границ плоской фигуры. Иными словами, это сумма длин ее сторон. Единица измерения периметра должна соответствовать единице измерения его сторон. Формула периметра многоугольника имеет вид Р = a + b + c…+ n, где Р — периметр, а вот а, b, с и n — длина каждой из сторон. Иначе вычисляется (или периметр круга): используется формула р = 2 * π * r, где r — радиус, а π — постоянное число, приблизительно равное 3,14. Рассмотрим несколько простых примеров, наглядно демонстрирующих, как найти периметр. В качестве образца возьмем такие фигуры как квадрат, параллелограмм и окружность.

Как найти периметр квадрата

Квадратом называется правильный четырехугольник, у которого равны все стороны и углы. Так как все стороны квадрата равны, сумму длин его сторон можно вычислить по формуле Р = 4 * a, где а — длина одной из сторон. Таким образом, со стороной 16,5 см равен Р = 4 * 16,5 = 66 см. Так же можно вычислить периметр равностороннего ромба.

Как найти периметр прямоугольника

Прямоугольник — это четырехугольник, все углы которого равны 90 градусам. Известно, что в такой фигуре, как прямоугольник, длины сторон равны попарно. Если ширина и высота прямоугольника имеют одинаковую длину, то он называется квадратом. Обычно длиной прямоугольника называют наибольшую из сторон, а шириной — наименьшую. Таким образом, чтобы получить периметр прямоугольника, необходимо удвоить сумму его ширины и высоты: P = 2 * (а + b), где а — высота, а b — ширина. Имея в наличии прямоугольник, одна сторона которого является длиной и равна 15 см, а другая шириной с установленным значением в 5 см, мы получим периметр, равный Р = 2 * (15 + 5) = 40 см.

Как найти периметр треугольника

Треугольник образован тремя отрезками, которые соединяются в точках (вершинах треугольника), не лежащих на одной и той же прямой. Треугольник называется равносторонним, если равны все три его стороны, и равнобедренным, если равных сторон две. Чтобы узнать периметр необходимо длину его стороны умножить на 3: Р = 3 * a, где а — одна из его сторон. Если стороны треугольника не равны между собой, необходимо провести операцию сложения: Р = а + b + с. Периметр равнобедренного треугольника со сторонами 33, 33 и 44 соответственно будет равен: P = 33 + 33 + 44 = 110 см.

Как найти периметр параллелограмма

Параллелограмм — это четырехугольник с попарно параллельными противоположными сторонами. Квадрат, ромб и прямоугольник являются частными случаями фигуры. Противоположные стороны любого параллелограмма равны, поэтому для вычисления его периметра воспользуемся формулой P = 2 (а + b). В параллелограмме со сторонами 16 см и 17 см сумма сторон, или периметр, равна Р = 2 * (16 + 17) = 66 см.

Как найти длину окружности

Окружность является замкнутой прямой, все точки которой расположены на равном удалении от центра. Длина окружности и ее диаметр всегда имеют одинаковое отношение. Это отношение выражено константой, записывается при помощи буквы π и равняется примерно 3,14159. Узнать периметр круга можно по произведению радиуса на 2 и на π. Получается, что длина окружности с радиусом в 15 см будет равна Р = 2 * 3,14159 * 15 = 94,2477

как найти периметр. Периметр и площадь Как измерить периметр фигуры

Знания о том, как найти периметр, учащиеся получают еще в начальной школе. Потом эта информация постоянно используется на протяжении всего курса математики и геометрии.

Общая для всех фигур теория

Стороны принято обозначать латинскими буквами. Причем их можно обозначать как отрезки. Тогда букв потребуется по две для каждой стороны и записанные большими. Или ввести обозначение одной буквой, которая обязательно будет маленькой.
Буквы всегда выбирают по алфавиту. Для треугольника они будут первыми тремя. У шестиугольника их будет 6 — от а до f. Это удобно для введения формул.

Теперь о том, как найти периметр. Он является суммой длин всех сторон фигуры. Количество слагаемых зависит от ее вида. Обозначается периметр латинской буквой Р. Единицы измерения совпадают с теми, которые даны для сторон.

Формулы периметров разных фигур

Для треугольника: Р=а+в+с. Если он равнобедренный, то формула преобразуется: Р=2а+в. Как найти периметр треугольника, если он равносторонний? Поможет такая: Р=3а.

Для произвольного четырехугольника: Р=а+в+с+d. Его частным случаем является квадрат, формула периметра: Р=4а. Есть еще прямоугольник, тогда требуется такое равенство: Р=2(а+в).

Как быть, если неизвестна длина одной или нескольких сторон треугольника?

Воспользоваться теоремой косинусов, если среди данных есть две стороны и угол между ними, который обозначается буквой А. Тогда до того, как найти периметр, придется посчитать третью сторону. Для этого пригодится такая формула: с² = а² + в² — 2 ав cos(А).

Частным случаем указанной теоремы является сформулированная Пифагором для прямоугольного треугольника. В ней значение косинуса прямого угла становится равным нулю, а значит, последнее слагаемое просто исчезает.

Бывают ситуации, когда узнать, как найти периметр треугольника, можно по одной стороне. Но при этом известны еще и углы фигуры. Здесь на помощь приходит теорема синусов, когда отношения длин сторон к синусам соответствующих противолежащих углов равны.

В ситуации, когда периметр фигуры нужно узнать по площади, пригодятся другие формулы. Например, если известен радиус вписанной окружности, то в вопросе о том, как находить периметр треугольника, пригодится следующая формула: S=р*r, здесь р — полупериметр. Его нужно вывести из данной формулы и умножить на два.

Примеры задач

Условие первой. Узнать периметр треугольника, стороны у которого 3, 4 и 5 см.
Решение. Нужно воспользоваться равенством, которое указано выше, и просто подставить в него данные в задаче значения. Расчеты легки, они приводят к числу 12 см.
Ответ. Периметр треугольника равен 12 см.

Условие второй. Одна сторона треугольника равна 10 см. Известно, что вторая на 2 см больше первой, а третья в 1,5 раза больше первой. Требуется вычислить его периметр.
Решение . Для того чтобы его узнать, потребуется сосчитать две стороны. Вторая определится как сумма 10 и 2, третья равна произведению 10 и 1,5. Потом останется только сосчитать сумму трех значений: 10, 12 и 15. Результатом будет 37 см.
Ответ. Периметр равняется 37 см.

Условие третьей. Имеются прямоугольник и квадрат. Одна сторона прямоугольника равна 4 см, а другая на 3 см больше. Нужно вычислить значение стороны квадрата, если его периметр меньше на 6 см, чем у прямоугольника.
Решение. Вторая сторона прямоугольника равна 7. Зная это, легко вычислить его периметр. Расчет дает 22 см.
Чтобы узнать сторону квадрата, нужно сначала вычесть 6 из периметра прямоугольника, а потом разделить полученное число на 4. В результате имеем число 4.
Ответ. Сторона квадрата 4 см.

Геометрия, если не ошибаюсь, в мое время изучалась с пятого класса и периметр был и есть одним из ключевых понятий. Итак, периметр — это сумма длин всех сторон (обозначается латинской литерой P) . Вообще, трактуют данный термин по разному, например,

• общая длина границы фигуры,
• длина всех ее сторон,
• сумма длин ее граней,
• длина ограничивающей фигуру линии,
• сумма всех длин сторон многоугольника

Для различных фигур существуют свои формулы определения периметра. Чтобы понять сам смысл, предлагаю самостоятельно вывести несколько несложных формул:

1. для квадрата,
2. для прямоугольника,
3. для параллелограмма,
4. для куба,
5. для параллелепипеда

Периметр квадрата

Для примера возьмем самое простое — периметр квадрата.

Все стороны квадрата равны. Пусть одна сторона носит название «a» (также, как и остальные три), тогда

P = a + a + a + a

или более компактная запись

Периметр прямоугольника

Усложним задачу и возьмем прямоугольник. В данном случае уже нельзя сказать, что все стороны равны, поэтому пусть длины сторон прямоугольника будут равны a и b.

Тогда формула будет иметь следующий вид:

P = a + b + a + b

Периметр параллелограмма

Аналогичная ситуация будет и с параллелограммом (см. периметр прямоугольника)

Периметр куба

Что же делать, если мы имеем дело с объемной фигурой? Например, возьмем куб. Куб имеет 12 сторон и все они равны. Соответственно, периметр куба можно вычислить следующим образом:

Периметр параллелепипеда

Ну, и для закрепления материала вычислим периметр параллелепипеда. Тут необходимо немного поразмышлять. Давайте делать это вместе. Как мы знаем, прямоугольный параллелепипед представляет собой фигуру, сторонами которой являются прямоугольники. У каждого параллелепипеда есть два основания. Возьмем одно из оснований и посмотрим на его стороны — они имеют длину a и b. Соответственно, периметр основания есть P = 2a + 2b. Тогда периметр двух оснований есть

(2a + 2b) * 2 = 4a + 4b

Но ведь у нас есть еще и сторона «c». Значит формула для вычисления периметра параллелепипеда будет иметь следующий вид:

P = 4a + 4b + 4c

Как видно из примеров выше, всё, что необходимо сделать для определения периметра фигуры — найти длину каждой из сторон, а затем их сложить.

В заключение хочется отметить, что не всякая фигура имеет периметр. К примеру, у шара периметра нет.

Периметр фигуры это длина всех ее сторон. Не все фигуры имеют периметр, например, шар не имеет периметра. Стандартное обозначение периметра в математике — буква P

Периметр квадрата

Пусть длина стороны квадрата равна a . Квадрат имеет четыре равных стороны, поэтому периметр квадрата есть P = a + a + a +a или:

Периметр прямоугольника

Пусть длины сторон прямоугольника равны a иb .
Длина всех его сторон есть P = a + b + a + b или:

Периметр параллелограмма

Пусть длины сторон параллелограмма равны a и b
Длина всех его сторон есть P = a + b + a + b , поэтому периметр параллелограмма есть:

Как видно, периметр параллелограмма равен периметру прямоугольника.

Периметр равнобедренной трапеции

Пускай длины параллельных сторон трапеции a и b , а длины двух других сторон равна c (Как известно, равнобедренная трапеция имеет две равные стороны).

P = a + b + c + c = a + b + 2c

Периметр равностороннего треугольника

Как известно, равносторонний треугольник имеет 3 равные стороны. Если длина стороны равна a , тогда формула нахождения периметра есть P = a + a + a

Периметр параллелепипеда

Параллелепипед есть призма, все стороны которой являются параллелограммами. (Прямоугольный параллелепипед это фигура, стороны которой — прямоугольники.)
Если стороны основания имеют длину a и b тогда периметр основания есть P = 2a + 2b . Каждый параллелепипед имеет два основания, поэтому периметр двух оснований равен (2a + 2b).2 = 4a + 4b . Как мы знаем, параметр это сумма всех сторон. Таким образом, мы должны сложить четыре раза c

P = 4a + 4b + 4c

Периметр куба

Куб это параллелепипед, все стороны которого являются квадратами (все грани равны).
Тогда, периметр куба есть число сторон*длина.
Каждый куб имеет 12 сторон.
Тогда, формула нахождения периметра куба имеет вид:

Где a — длина его стороны.

Как найти Периметр различных геометрических форм

Возникли проблемы в понимании того, как найти периметр различных геометрических фигур? Бизнес сайт приходит к вам на помощь посредством облегчения геометрии, чем когда-либо!Удовольствие FactThe периметру или окружности Земли составляет 24,901 миль, я. э. почти 40,075 км!В математике, геометрии рассматриваются формы, размеры, взаиморасположение, трехмерная ориентация фигур в пространстве. Она имеет дело с тремя основными измерениями фигур:площади, объема и периметра.

Площадь является мерой степени двумерной фигуры или формы; поверхность может быть описана как степень поверхности объекта. Это мера в трехмерном пространстве вблизи объекта.

По периметру можно просто охарактеризовать как длина пути, который окружает двумерной формы. Другими словами, это расстояние вокруг фигуры. Давайте теперь взглянем на Как найти периметр различных геометрических форм.

Индекс
Площадь
Прямоугольник
Круг
Полуокружность

Сектор
Треугольник
Трапециевидные
Полигон
Площадь
Квадрат-это четырехугольник, который имеет все четыре стороны и четыре угла равны (все 90°).

Пример: чтобы найти периметр квадрата со стороной 5 см, мы используем формулу, показанную на рис..
Р = А + А + А + А
Р = 5 + 5 + 5 + 5
Р = 20 см
Эта же формула может использоваться для вычисления периметра ромба..
Обратно в индекс
Прямоугольник
Прямоугольник-это четырехугольник, который имеет все четыре угла равны (все 90°). Противоположные стороны прямоугольника равны (тогда как на смежных сторонах нет).

Пример: чтобы найти периметр прямоугольника, мы используем формулу, показанную на рис..
л = 15 см
б = 25 см
Р = 2 (15 + 25)
Р = 2 (40)
Р = 80 см
Вы можете использовать ту же формулу, чтобы найти периметр параллелограмма.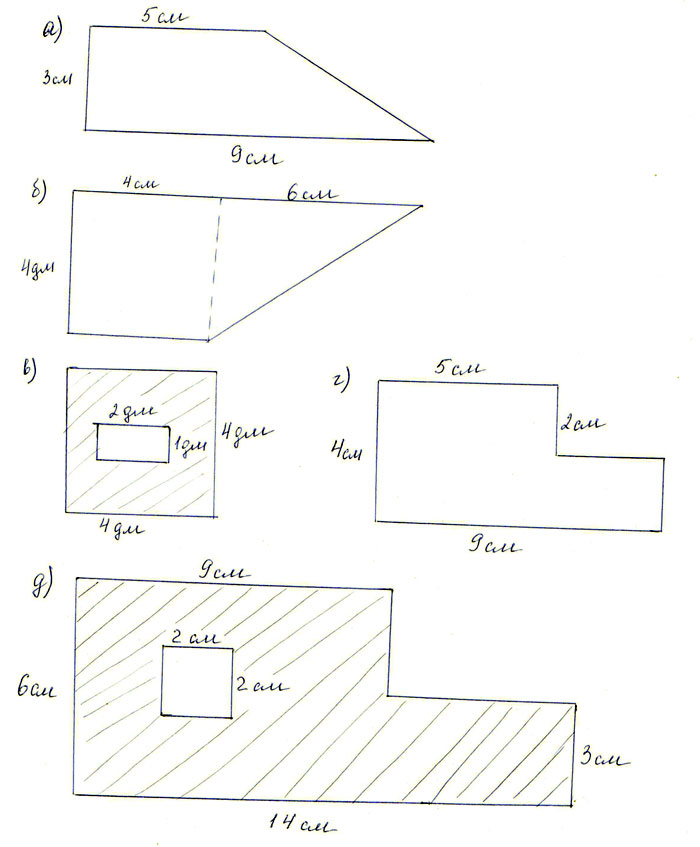
Обратно в индекс
Круг
Окружность может быть описана как множество точек, находящихся на равном расстоянии от определенной точки (известный как центр). Периметр окружности называется окружности, обозначается с.

Пример: найти длину окружности, мы используем формулу, показанную на рис..
Если C = 2πR и πд
С = 2 Х 3. 14 х 7 или 3. 14 х 14
С = 43. 96 см
Обратно в индекс
ПОЛУОКРУЖНОСТЬ
Полукольцом, проще говоря, наполовину окружность, его периметр будет половина этого круга.

Пример: чтобы найти периметр полукруга, мы используем формулу, показанную на рис..
р = 7 см или D = 14 см (д = р + р)
Р = πR и πд/2
Р = 2 Х 3. 14 х 7 или 3. 14 х 14/2
П = 21. 98 см
Обратно в индекс
Сектор
Сектор можно охарактеризовать как часть окружности.

Пример: чтобы найти периметр сектора, мы используем формулу, показанную на рис..

ϴ = 60°
р = 7 см
Р = 60/360 Х 2 Х 3. 14 х 7
Р = 7. 33 см
Обратно в индекс
Треугольник
Треугольник-это многоугольник, который имеет три стороны и три вершины.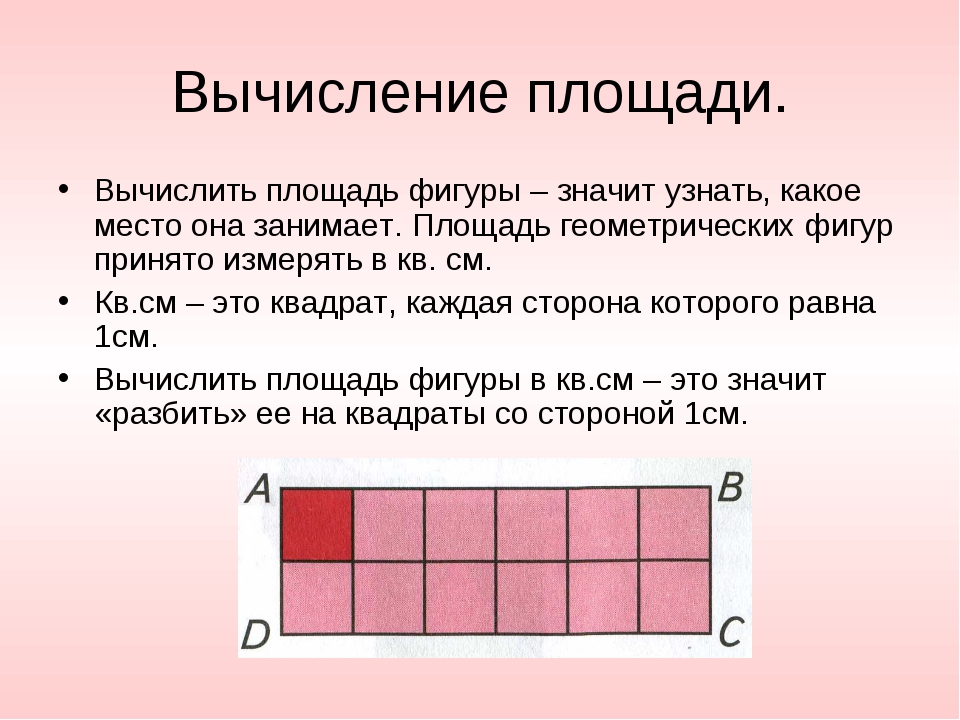 Давайте учитывать три случая для того, чтобы определить его периметр.

один. Когда все три стороны известны.

Чтобы найти периметр треугольника, мы используем формулу, показанную на рис..
а = 14 см
б = 16 см
с = 15 см
Р = 14 + 16 + 15
Р = 45 см
б. Для прямоугольного треугольника если его гипотенуза неизвестна.

Чтобы найти периметр прямоугольного треугольника, мы используем формулу, показанную на рис..
Б = 3 см
ч = 4 см
П = б + ч + √ Б2 + ч 2
П = 3 + 4 + √ 32 + 4 2
Р = 3 + 4 + 5
Р = 12 см

Если любой другой стороны неизвестно, можно использовать формулу Пифагора найти бок сначала, а потом вычислить периметр.
с. Для любого другого треугольника, когда только две стороны и угол они известны.

Прежде всего нам нужно найти длину стороны, используя закон косинусов,
Когда А, B и C длины сторон треугольника, а, b и C имеют противоположные углы сторонами A, B и C, соответственно, мы можем найти длину неизвестной стороны (скажем, с) по формуле:

С2 = а 2 + Б 2 — в 2. б потому что(с)

Например
А = 4 см
Б = 2 см
С2 = 4 2 + 2 2 — 2 4. 2 соѕ(45)
С2 = 16 + 4 — 2 (0. 876)
С2 = 20 — 1. 752
С2 = 18. 284
с = 4. 272 см

Р = А + В + С
Р = 4 + 2 + 4. 272
П = 10. 272 см
Обратно в индекс
ТРАПЕЦИЕВИДНЫЕ
Трапецией называется четырехугольник, по крайней мере одну пару параллельных линий. Параллельные линии называются основания трапеции, и с другой стороны не известно как ноги трапеции. Расстояние между параллельными линиями, называется высотой трапеции.
Давайте рассмотрим три различных сценариях, чтобы найти периметр.

один. Когда всем сторонам известно.

А = 4 см
б = 16 см
с = 5 см
д = 8 см
Р = 4 + 16 + 5 + 8
Р = 33 см
б. Когда его стороны (ноги) неизвестны.

Чтобы найти периметр трапеции, мы используем формулу, показанную на рис..
б = 16 см
ч = 3 см
д = 8 см
П = б + д + ч
1
+
1
Грех(С)
Грех(А)

Р = 16 + 8 + 3
1
+
1
Грех(53)
Грех(45)

Р = 16 + 8 + 33. 3
П = 57. 3 см
с. Когда один из базовых и высота неизвестны.

Представьте, если бы мы должны были сократить трапецевидной с двух сторон таким образом, что длины оснований равны, и когда мы присоединяемся к вырезанной части, мы получим треугольник, как показано на рисунке.

Когда ∠и ∠с равны; все три угла по 60°. Этот треугольник-равносторонний треугольник, и, следовательно, когда длина стороны добавляется в базу, мы получим длину большего основания.
Когда углы равны; сумма углов вычитал на 180°.

Площадь этого треугольника можно рассчитать по формуле
А = ½ Х Х Х sin (Б)
Найти периметр трапеции,
А = 4 см
с = 6 см
д = 11 см
∠ а = 53°
∠ с = 65°
∠ Б = 78°
Площадь = ½ х 4 х 6 х sin 78
Площадь = 6. 12 см2
Основание треугольника=
Площадь
½ Х х грех(с)

База =
6. 12
½ Х 4 х sin(65)

База =
6. 12
2 х 0. 826

Основание = 3. 70 см
Основание трапеции = 11 + 3. 70 = 14. 70 см

Теперь у нас есть бока и основание трапеции, мы можем найти периметр.
Р = 14. 7 + 4 + 6 + 11
П = 35. 7 см
Обратно в индекс
Полигон
Любая замкнутая фигура, где отрезки не пересекаются друг с другом приводит к полигону. Сумма внутренних углов многоугольника всегда 360°, и они названы в зависимости от количества сторон, которыми они обладают.

один. Правильный многоугольник имеет все равные стороны, так что когда число сторон и длину каждой стороны известен периметр многоугольника может быть рассчитана с использованием формулы, показанной на рис..

Пример: если шестигранник имеет стороны длиной 5 см, его периметр можно вычислить, как показано ниже.
н = 6 (шестиугольник имеет шесть сторон)
с = 5 см
Р = 6 х 5
Р = 30 см
б. При длине стороны многоугольника не известны, то его периметр может быть рассчитана с помощью формулы, приведенной ниже.

Х = 2 х х Тан (180/п)
Здесь a-apothem.
Apothem-это отрезок от центра многоугольника до середины боковой.

Ы = 2 х R х Тан (180/п)
R-радиус.
Расстояние от центра правильного многоугольника на любую вершину.

Пример: на шестигранник apothem 4 см, его сторона может быть вычислена, как показано ниже.
с = 2 х 4 х Тан (180/6)
х = 8 х Тан (30)
ы = 8 х 0. 58
ы = 4. 62 см

Р = 6 х 4. 62 = 27. 71 см

Для шестиугольника радиусом 4 см, его сторона может быть вычислена, как показано ниже.
х = 2 х 4 х sin (180/6)
ы = 8 х sin (30)
ы = 8 х 0. 5
ы = 4. 00 см

Р = 6 х 4. 00 = 24 см
с. Для неправильного многоугольника, если все его стороны равны, мы можем вычислить его периметр, просто добавив длины всех его сторон.

Пример: неправильного многоугольника из шести сторон
С1 = 8 см
С2 = 6 см
С3 = 4 см
С4 = 7см
С5 = 5 см
С6 = 4 см

Р = С1 + С2 + С3 + С4 + С5 + С6
П = 8 + 6 + 4 + 7 + 5 + 4
Р = 36 см
Обратно в индекс
Мы знаем, что геометрия может быть немного сложной на первый (поверьте, мы знаем), но продолжать практиковаться, и вы, несомненно, становится лучше с каждой попыткой.

Умение находить периметр прямоугольника очень важно для решения многих геометрических задач . Ниже приведена по нахождению периметра разных прямоугольников.

Как найти периметр обычного прямоугольника

Обычный прямоугольник — четырехугольник, у которого параллельные стороны равны и все углы = 90º. Для нахождения его периметра существует 2 способа:

Складываем все стороны.

Вычислите периметр прямоугольника, есть его ширина равна 3 см., а длина — 6.

Решение (последовательность действий и рассуждения):

• Так как нам известны ширина и длина прямоугольника, найти его периметр не составит труда. Ширина параллельна ширине, а длина длине. Таким образом, в обычном прямоугольнике 2 ширины и 2 длины.
• Складываем все стороны (3 + 3 + 6 + 6) = 18 см.

Ответ: P = 18 см.

Второй способ заключается в следующем:

Нужно сложить ширину и длину, и умножить на 2. Формула этого способа имеет следующий вид: 2×(a + b), где a — ширина, b — длина.

В рамках данной задачи получим такое решение:

2×(3 + 6) = 2×9 = 18.

Ответ: P = 18.

Как найти периметр прямоугольника — квадрат

Квадрат является правильным четырехугольником. Правильным потому, что все его стороны и углы равны. Для нахождения его периметра так же существует два способа:

• Сложить все его стороны.
• Умножить его сторону на 4.

Пример: Найти периметр квадрата, если его сторона = 5 см.

Знания о том, как найти периметр, учащиеся получают еще в начальной школе . Потом эта информация постоянно используется на протяжении всего курса математики и геометрии.

Общая для всех фигур теория

Стороны принято обозначать латинскими буквами. Причем их можно обозначать как отрезки. Тогда букв потребуется по две для каждой стороны и записанные большими. Или ввести обозначение одной буквой, которая обязательно будет маленькой.
Буквы всегда выбирают по алфавиту. Для треугольника они будут первыми тремя. У шестиугольника их будет 6 — от а до f. Это удобно для введения формул.

Теперь о том, как найти периметр. Он является суммой длин всех сторон фигуры. Количество слагаемых зависит от ее вида. Обозначается периметр латинской буквой Р. Единицы измерения совпадают с теми, которые даны для сторон.

Формулы периметров разных фигур

Для треугольника: Р=а+в+с. Если он равнобедренный, то формула преобразуется: Р=2а+в. Как найти периметр треугольника, если он равносторонний? Поможет такая: Р=3а.

Для произвольного четырехугольника: Р=а+в+с+d. Его частным случаем является квадрат, формула периметра: Р=4а. Есть еще прямоугольник, тогда требуется такое равенство: Р=2(а+в).

Как быть, если неизвестна длина одной или нескольких сторон треугольника?

Воспользоваться теоремой косинусов, если среди данных есть две стороны и угол между ними, который обозначается буквой А. Тогда до того, как найти периметр, придется посчитать третью сторону. Для этого пригодится такая формула: с² = а² + в² — 2 ав cos(А).

Частным случаем указанной теоремы является сформулированная Пифагором для прямоугольного треугольника. В ней значение косинуса прямого угла становится равным нулю , а значит, последнее слагаемое просто исчезает.

Бывают ситуации, когда узнать, как найти периметр треугольника, можно по одной стороне. Но при этом известны еще и углы фигуры. Здесь на помощь приходит теорема синусов, когда отношения длин сторон к синусам соответствующих противолежащих углов равны.

В ситуации, когда периметр фигуры нужно узнать по площади, пригодятся другие формулы. Например, если известен радиус вписанной окружности, то в вопросе о том, как находить периметр треугольника, пригодится следующая формула: S=р*r, здесь р — полупериметр. Его нужно вывести из данной формулы и умножить на два.

Примеры задач

Условие первой. Узнать периметр треугольника, стороны у которого 3, 4 и 5 см.
Решение. Нужно воспользоваться равенством, которое указано выше, и просто подставить в него данные в задаче значения. Расчеты легки, они приводят к числу 12 см.
Ответ. Периметр треугольника равен 12 см.

Условие второй. Одна сторона треугольника равна 10 см. Известно, что вторая на 2 см больше первой, а третья в 1,5 раза больше первой. Требуется вычислить его периметр.
Решение . Для того чтобы его узнать, потребуется сосчитать две стороны. Вторая определится как сумма 10 и 2, третья равна произведению 10 и 1,5. Потом останется только сосчитать сумму трех значений: 10, 12 и 15. Результатом будет 37 см.
Ответ. Периметр равняется 37 см.

Условие третьей. Имеются прямоугольник и квадрат. Одна сторона прямоугольника равна 4 см, а другая на 3 см больше. Нужно вычислить значение стороны квадрата, если его периметр меньше на 6 см, чем у прямоугольника.
Решение. Вторая сторона прямоугольника равна 7. Зная это, легко вычислить его периметр. Расчет дает 22 см.
Чтобы узнать сторону квадрата, нужно сначала вычесть 6 из периметра прямоугольника, а потом разделить полученное число на 4. В результате имеем число 4.
Ответ. Сторона квадрата 4 см.

Определение периметра и площади геометрических фигур — важная задача, которая возникает при решении многих практических или бытовых задач. Если вам требуется поклеить обои, установить забор, рассчитать расход краски или кафеля, то вам обязательно придется иметь дело с геометрическими расчетами.

Для решения перечисленных бытовых вопросов вам потребуется работать с самыми разными геометрическими фигурами . Мы представляем вам каталог онлайн-калькуляторов, которые позволяют вычислить параметры наиболее популярных плоских фигур. Рассмотрим их.

Круг

Частные случаи

Четырехугольник с одинаковыми сторонами. Параллелограмм становится ромбом в случаях, если его диагонали пересекаются под углом 90 градусов и являются биссектрисами своих углов.

Это параллелограмм с прямыми углами. Кроме того, параллелограмм считается прямоугольником, если его стороны и диагонали отвечают условиям теоремы Пифагора.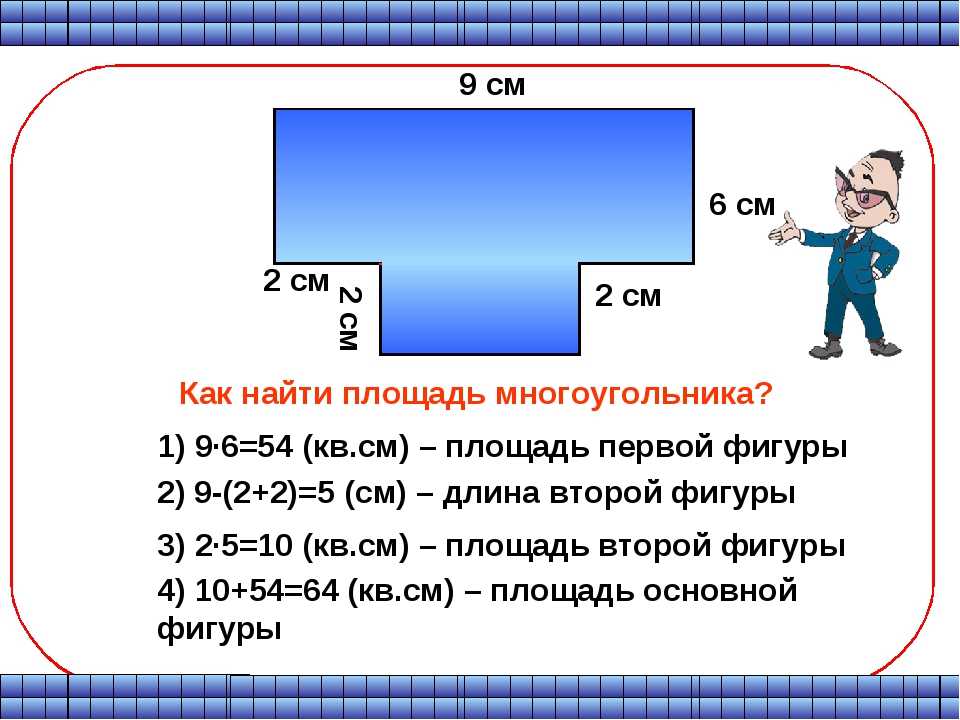

Это параллелограмм, у которого все стороны равны и все углы равны. Диагонали квадрата полностью повторяют свойства диагоналей прямоугольника и ромба, что делает квадрат уникальной фигурой, которая характеризуется максимальной симметрией.

Многоугольник

Правильный полигон — это выпуклая фигура на плоскости, которая имеет равные стороны и равные углы . В зависимости от количества сторон многоугольники имеют собственные названия:

• — пентагон;
• — гексагон;
• восемь — октагон;
• двенадцать — додекагон.

И так далее. Геометры шутят, что круг — это многоугольник с бесконечным количеством углов. Наш калькулятор запрограммирован на определение периметров и площадей только правильных многоугольников. Он использует общие формулы для всех правильных полигонов. Для вычисления периметра используется формула:

где n – количество сторон многоугольника, a – длина стороны.

Для определения площади используется выражение:

S = n/4 × a^2 × ctg(pi/n).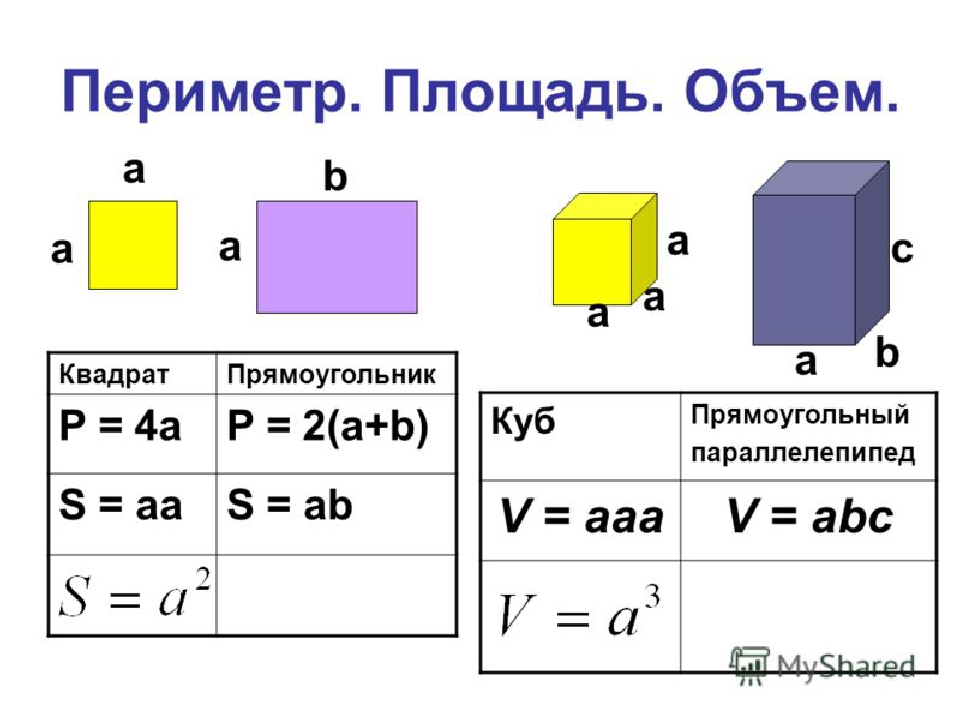

Подставляя соответствующее n, мы можем подобрать формулу для любого правильного многоугольника, к которым также относятся равносторонний треугольник и квадрат.

Многоугольники имеют большое распространение в реальной жизни. Так форму пятиугольника имеет здание министерства обороны США — Пентагон, гексагона — пчелиные соты или кристаллы снежинки, октагона — дорожные знаки. Кроме того, многие простейшие, например радиолярии, имеют форму правильных полигонов.

Примеры из реальной жизни

Давайте рассмотрим пару примеров использования нашего калькулятора в реальных расчетах.

Покраска забора

Покраска поверхностей и расчет краски — это одни из самых очевидных бытовых задач, в которых требуются минимальные математические расчеты. Если нам нужно покрасить забор, высота которого составляет 1,5 метра, а длина 20 метров, то сколько потребуется банок краски? Для этого нужно узнать суммарную площадь забора и расход лакокрасочных материалов на 1 квадратный метр. Мы знаем, что расход эмали составляет 130 грамм на метр. Теперь определим площадь забора, используя калькулятор для вычисления площади прямоугольника. Она составит S = 30 квадратных метров . Естественно, что забор мы будем красить с обеих сторон, поэтому площадь для покраски увеличится до 60 квадратов. Тогда нам понадобится 60 × 0,13 = 7,8 килограмм краски или три стандартных банки по 2,8 килограмма.

Отделка бахромой

Пошив одежды — еще одна отрасль, в которой необходимы обширные геометрические познания. Пусть нам надо отделать бахромой платок, который представляет собой равнобедренную трапецию со сторонами 150, 100, 75 и 75 см. Для вычисления расхода бахромы нам потребуется узнать периметр трапеции. В этом нам и пригодится онлайн-калькулятор. Введем эти данные ячейки и получим ответ:

Таким образом, нам понадобится 4 м бахромы для отделки платка.

Заключение

Плоские фигуры составляют реальный мир вокруг. Мы часто задавались в школе вопросом, пригодится ли нам геометрия в будущем? Выше приведенные примеры показывают, что математика постоянно используется в повседневной жизни . И если площадь прямоугольника для нас привычна, то вычислить площадь додекагона может оказаться трудной задачей . Используйте наш каталог калькуляторов для решения школьных заданий или бытовых вопросов.

Как измерить периметр фигуры. Периметр квадрата и прямоугольника. Способы определения и примеры решения. Подготовка к изучению нового материала

Прямоугольник обладает многими отличительными особенностями, исходя из которых, выработаны правила вычисления его различных числовых характеристик. Итак, прямоугольник:

Плоская геометрическая фигура;
Четырехугольник;
Фигура, у которой противоположные стороны равны и параллельны, все углы прямые.

Периметр – это общая длина всех сторон фигуры.

Вычисление периметра прямоугольника — довольно простая задача.

Все, что вам нужно знать, это ширину и длину прямоугольника. Поскольку прямоугольник имеет две равные длины и две равные ширины, измеряется только одна сторона.

Периметр прямоугольника равен удвоенной сумме 2-х его сторон длины и ширины.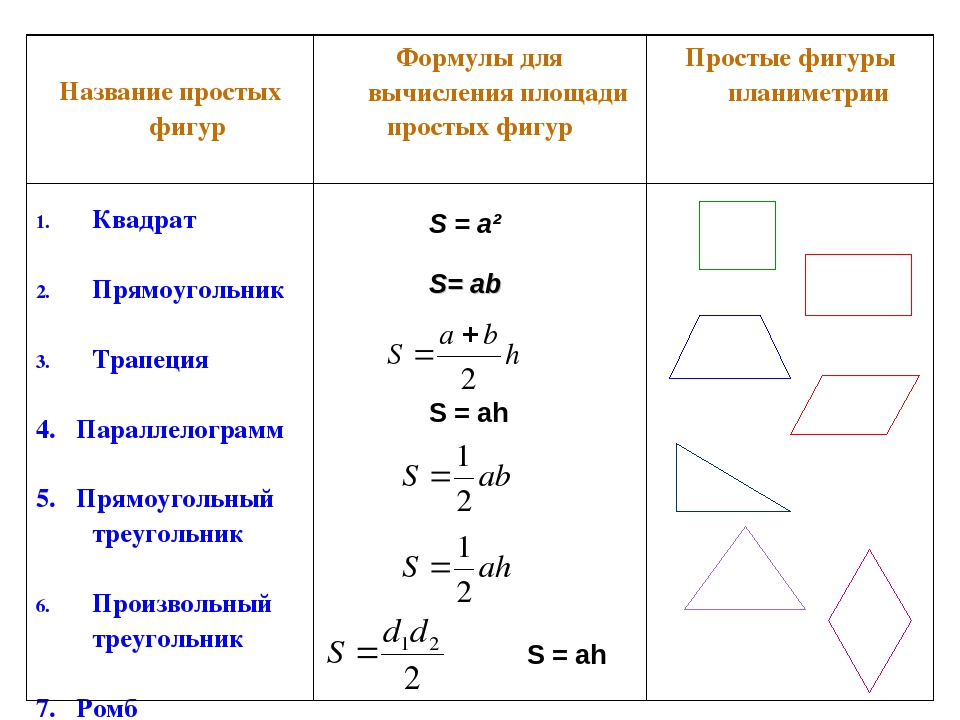

P = (a + b) 2, где a — длина прямоугольника, b — ширина прямоугольника.

Так же периметр прямоугольника можно найти при помощи суммы всех сторон.

P= a+a+b+b, где а– длина прямоугольника, b – ширина прямоугольника.

Периметр квадрата — это длина стороны квадрата, умноженная на 4.

P = a 4, где a — длина стороны квадрата.

Дополнение: Нахождение найти площади и периметра прямоугольников

В программе обучения за 3 класс предусмотрено изучение многоугольников и их особенностей. Для того чтобы понять, как найти периметр прямоугольника и площадь, разберемся, что подразумевается под этими понятиями.

Основные понятия

Нахождение периметра и площади требует знания некоторых терминов. К ним относятся:

1. Прямой угол. Образуется из 2 лучей, имеющих общее начало в виде точки. При знакомстве с фигурами (3 класс) прямой угол определяют с помощью угольника.
2. Прямоугольник. Это четырехугольник, все углы которого являются прямыми. Его стороны называют длиной и шириной. Как известно, противоположные стороны этой фигуры равны.
3. Квадрат. Является четырехугольником, все стороны которого равны.

При знакомстве с многоугольниками их вершины могут называться АВСД. В математике принято именовать точки на чертежах буквами латинского алфавита. В названии многоугольника перечисляют все вершины без пропусков, например, треугольник ABC.

Вычисление периметра

Периметр многоугольника — это сумма длин всех его сторон. Эта величина обозначается латинской буквой P. Уровень знаний для предложенных примеров — 3 класс.

Задача №1: «Начертите прямоугольник 3 см шириной и 4 см длиной с вершинами ABCD. Найдите периметр прямоугольника ABCD».

Формула будет выглядеть так: P=AB+BC+CD+AD либо P=AB×2+BC×2.

Ответ: P=3+4+3+4=14 (см) либо P=3×2 + 4×2=14 (см).

Задача №2: «Как найти периметр прямоугольного треугольника ABC, если значения сторон равны 5, 4 и 3 см?».

Ответ: P=5+4+3=12 (см).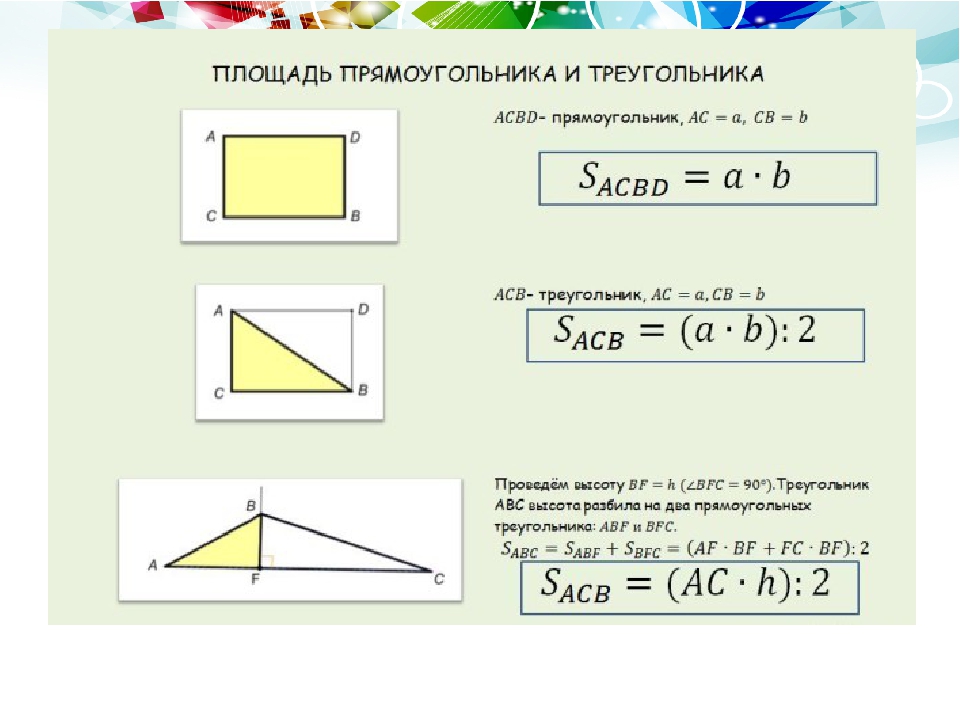

Задача №3: «Найдите периметр прямоугольника, одна сторона которого равна 7 см, а другая на 2 см длиннее».

Ответ: P=7+9+7+9=32 (см).

Задача №4: «Соревнования по плаванию проходили в бассейне, периметр которого составляет 120 м. Сколько метров проплыл участник соревнований, если ширина бассейна 10 м?».

В данной задаче стоит вопрос, как найти длину бассейна. Для решения найдите длины сторон прямоугольника. Ширина известна. Сумма длин двух неизвестных сторон должна составить 100 м. 120-10×2=100. Чтобы узнать расстояние, которое преодолел пловец, нужно разделить полученный результат на 2. 100:2=50.

Ответ: 50 (м).

Вычисление площади

Более сложной величиной является площадь фигуры. Для ее измерения используют мерки. Эталоном среди мерок являются квадраты.

Площадь квадрата со стороной 1 см равна 1 см². Квадратный дециметр обозначен как дм², а квадратный метр — м².

Области применения единиц измерения могут быть такими:

1. В см² измеряют маленькие предметы, например фотографии, обложки учебников, листы бумаги.
2. В дм² можно измерить географическую карту, оконное стекло, картину.
3. Для измерения пола, квартиры, земельного участка используют м².

Если начертить прямоугольник 3 см длиной и 1 см шириной и разбить на квадраты со стороной 1 см, то в нем поместится 3 квадрата, а значит, его площадь составит 3 см². Если прямоугольник разбит на квадраты, найдем периметр прямоугольника также без затруднений. В данном случае он равен 8 см.

Другой способ посчитать количество квадратов, вмещающихся в фигуру, — это использование палетки. Начертим на кальке квадрат площадью 1 дм², что составляет 100 см². Поместим кальку на фигуру и посчитаем число квадратных сантиметров в одном ряду. После этого выясним количество рядов, а затем перемножим значения. Значит, площадь прямоугольника — это произведение его длины и ширины.

Способы сравнения площадей:

1. На глаз. Иногда достаточно просто взглянуть на предметы, поскольку в некоторых случаях и невооруженным глазом видно, что одна фигура занимает больше места, как, например, учебник, лежащий на столе рядом с пеналом.
2. Наложение. Если фигуры совпадают при наложении, их площади равны. Если же одна из них полностью помещается внутри второй, то ее площадь меньше. Места, занимаемые тетрадным листом и страницей из учебника, можно сравнить, наложив их друг на друга.
3. По количеству мерок. Фигуры при наложении могут и не совпадать, однако иметь одинаковую площадь. Сравнить в этом случае можно, подсчитав количество квадратов, на которые разбита фигура.
4. Числа. Сравниваются численные значения, измеренные одной и той же меркой, например, в м².

Пример №1: «Швея сшила детское одеяло из квадратных разноцветных лоскутков. Один лоскуток длиной 1 дм, в ряду по 5 штук. Сколько дециметров ленты понадобится швее для обработки краев одеяла, если известна площадь 50 дм²?».

Чтобы решить задачу, нужно ответить на вопрос, как найти длину прямоугольника. Далее найдем периметр прямоугольника, составленного из квадратов. Из задачи ясно, что ширина одеяла — 5 дм, вычисляем длину, разделив 50 на 5, и получаем 10 дм. Теперь найдите периметр прямоугольника со сторонами 5 и 10. P=5+5+10+10=30.

Ответ: 30 (м).

Пример №2: «На раскопках обнаружен участок, где могут находиться древние сокровища. Сколько территории придется исследовать ученым, если известен периметр 18 м и ширина прямоугольника 3 м?».

Определим длину участка, проделав 2 действия. 18-3×2=12. 12:2=6. Искомая территория будет также равна 18 м² (6×3=18).

Ответ: 18 (м²).

Таким образом, зная формулы, вычислить площадь и периметр не составит труда, а приведенные выше примеры помогут попрактиковаться в решении математических задач.

В следующих тестовых заданиях требуется найти периметр фигуры, изображенной на рисунке.

Найти периметр фигуры можно разными способами. Можно преобразовать исходную фигуру таким образом, чтобы периметр новой фигуры можно было бы легко вычислить (например, перейти к прямоугольнику).

Другой вариант решения — искать периметр фигуры непосредственно (как сумму длин всех её сторон). Но в этом случае нельзя полагаться только на рисунок, а находить длины отрезков, исходя из данных задачи.

Хочу предупредить: в одном из заданий среди предложенных вариантов ответов я не нашла того, который получился у меня.

C) .

Перенесем стороны маленьких прямоугольников с внутренней области во внешнюю. В результате большой прямоугольник замкнулся. Формула для нахождения периметра прямоугольника

В данном случае, a=9a, b=3a+a=4a. Таким образом, P=2(9a+4a)=26a. К периметру большого прямоугольника прибавляем сумму длин четырех отрезков, каждый из которых равен 3a. В итоге, P=26a+4∙3a=38a .

C) .

После переноса внутренних сторон маленьких прямоугольников во внешнюю область, получаем большой прямоугольник, периметр которого равен P=2(10x+6x)=32x, и четыре отрезка, два — диной по x, два — по 2x.

Итого, P=32x+2∙2x+2∙x=38x .

?) .

Перенесем 6 горизонтальных «ступенек» из внутренней части во внешнюю. Периметр полученного большого прямоугольника равен P=2(6y+8y)=28y. Осталось найти сумму длин отрезков внутри прямоугольника 4y+6∙y=10y. Таким образом, периметр фигуры равен P=28y+10y=38y .

D) .

Перенесем вертикальные отрезки из внутренней области фигуры влево, во внешнюю область. Чтобы получить большой прямоугольник, перенесём одни из отрезков длиной 4x в нижний левый угол.

Периметр исходной фигуры найдём как сумму периметра этого большого прямоугольника и длин оставшихся внутри трёх отрезков P=2(10x+8x)+6x+4x+2x=48x .

E) .

Перенеся внутренние стороны маленьких прямоугольников во внешнюю область, получим большой квадрат. Его периметр равен P=4∙10x=40x. Чтобы получить периметр исходной фигуры, нужно у периметру квадрата прибавить сумму длин восьми отрезков, каждый длиной 3x. Итого, P=40x+8∙3x=64x .

B) .

Перенесём все горизонтальные «ступеньки» и вертикальные верхние отрезки во внешнюю область. Периметр полученного прямоугольника равен P=2(7y+4y)=22y. Чтобы найти периметр исходной фигуры, нужно к периметру прямоугольника прибавить сумму длин четырех отрезков, каждый длиной y: P=22y+4∙y=26y .

D) .

Перенесем из внутренней области во внешнюю все горизонтальные линии и передвинем две вертикальные внешние линии в левом и правом углах, соответственно, на z левее и правее. В результате получим большой прямоугольник, периметр которого равен P=2(11z+3z)=28z.

Периметр исходной фигуры равен сумме периметра большого прямоугольника и длин шести отрезков по z: P=28z+6∙z=34z .

B) .

Решение полностью аналогично решению предыдущего примера. После преобразования фигуры находим периметр большого прямоугольника:

P=2(5z+3z)=16z. К периметру прямоугольника прибавляем сумму длин оставшихся шести отрезков, каждый из которых равен z: P=16z+6∙z=22z .

Урок и презентация на тему: «Периметр и площадь прямоугольника»

Дополнительные материалы
Уважаемые пользователи, не забывайте оставлять свои комментарии, отзывы, пожелания. Все материалы проверены антивирусной программой.

Обучающие пособия и тренажеры в интернет-магазине «Интеграл» для 3 класса
Тренажер для 3 класса «Правила и упражнения по математике»
Электронное учебное пособие для 3 класса «Математика за 10 минут»

Что такое прямоугольник и квадрат

Прямоугольник – это четырёхугольник, у которого все углы прямые. Значит, противоположные стороны равны друг другу.

Квадрат – это прямоугольник, у которого равны и стороны, и углы. Его называют правильным четырёхугольником.

Четырёхугольники, в том числе прямоугольники и квадраты, обозначаются 4 буквами – вершинами. Для обозначения вершин используют латинские буквы: A, B, C, D …

Пример.

Читается так: четырёхугольник ABCD; квадрат EFGH.

Что такое периметр прямоугольника? Формула расчета периметра

Периметр прямоугольника – это сумма длин всех сторон прямоугольника или сумма длины и ширины, умноженная на 2.

Периметр обозначается латинской буквой P . Так как периметр — это длина всех сторон прямоугольника, то он периметр записывается в единицах длины: мм, см, м, дм, км.

Например, периметр прямоугольника АВСD обозначается как P ABCD , где А, В, С, D — это вершины прямоугольника.

Запишем формулу периметра четырехугольника ABCD:

P ABCD = AB + BC + CD + AD = 2 * AB + 2 * BC = 2 * (AB + BC)

Пример.
Задан прямоугольник ABCD со сторонами: AB=СD=5 см и AD=BC=3 см.
Определим P ABCD .

Решение:
1. Нарисуем прямоугольник ABCD с исходными данными.
2. Напишем формулу для расчета периметра данного прямоугольника:

P ABCD = 2 * (AB + BС)

P ABCD = 2 * (5 см + 3 см) = 2 * 8 см = 16 см

Ответ: P ABCD = 16 см.

Формула расчета периметра квадрата

У нас есть формула для определения периметра прямоугольника.

P ABCD = 2 * (AB + BC)

Применим её для определения периметра квадрата. Учитывая, что все стороны квадрата равны, получаем:

P ABCD = 4 * AB

Пример.
Задан квадрат ABCD со стороной, равной 6 см. Определим периметр квадрата.

Решение.
1. Нарисуем квадрат ABCD с исходными данными.

2. Вспомним формулу расчета периметра квадрата:

P ABCD = 4 * AB

3. Подставим в формулу наши данные:

P ABCD = 4 * 6 см = 24 см

Ответ: P ABCD = 24 см.

Задачи на нахождение периметра прямоугольника

1. Измерь ширину и длину прямоугольников. Определи их периметр.

2. Нарисуй прямоугольник ABCD со сторонами 4 см и 6 см. Определи периметр прямоугольника.

3. Нарисуй квадрат СEOM со стороной 5 см. Определи периметр квадрата.

Где используется расчет периметра прямоугольника?

1. Задан участок земли, его нужно обнести забором. Какой длины будет забор?

В данной задаче необходимо точно рассчитать периметр участка, чтобы не купить лишний материал для постройки забора.

2. Родители решили сделать ремонт в детской комнате. Необходимо знать периметр комнаты и её площадь, чтобы правильно рассчитать количество обоев.
Определи длину и ширину комнаты, в которой ты живешь. Определи периметр своей комнаты.

Что такое площадь прямоугольника?

Площадь – это числовая характеристика фигуры. Площадь измеряется квадратными единицами длины: см 2 , м 2 , дм 2 и др. (сантиметр в квадрате, метр в квадрате, дециметр в квадрате и т.д.)
В вычислениях обозначается латинской буквой S .

Для определения площади прямоугольника необходимо длину прямоугольника умножить на его ширину.
Площадь прямоугольника вычисляется умножением длины АК на ширину КМ. Запишем это в виде формулы.

S AKMO = AK * KM

Пример.
Чему равна площадь прямоугольника AKMO, если его стороны равны 7 см и 2 см?

S AKMO = AK * KM = 7 см * 2 см = 14 см 2 .

Ответ: 14 см 2 .

Формула вычисления площади квадрата

Площадь квадрата можно определить, умножив сторону саму на себя.

Пример.
В данном примере площадь квадрата вычисляется умножением стороны АB на ширину BC, но так как они равны, получается умножение стороны AB на AB.

S AВСО = AB * BC = AB * AB

Пример.
Определи площадь квадрата AKMO со стороной 8 см.

S AKMО = AK * KM = 8 см * 8 см = 64 см 2

Ответ: 64 см 2 .

Задачи на нахождение площади прямоугольника и квадрата

1.Задан прямоугольник со сторонами 20 мм и 60 мм. Вычисли его площадь. Запиши ответ в квадратных сантиметрах.

2. Был куплен дачный участок размером 20 м на 30 м. Определи площадь дачного участка, ответ запиши в квадратных сантиметрах.

Периметр — это сумма длин всех сторон многоугольника.

• Для вычисления периметра геометрических фигур используются специальные формулы, где периметр обозначается буквой «P». Название фигуры рекомендуется писать маленькими буквами под знаком «P», чтобы знать чей периметр ты находишь.
• Периметр измеряется в единицах длины: мм, см, м, км и т.д.

Отличительные особенности прямоугольника

• Прямоугольник – это четырехугольник.
• Все параллельные стороны равны
• Все углы = 90º.
• Например в повседневной жизни прямоугольник может встречаться в виде — книги, монитора, крышки от стола или двери.

Как вычислить периметр прямоугольника

Существует 2 способа его нахождения:

• 1 способ. Складываем все стороны. P = a + а + b + b
• 2 способ. Сложить ширину и длину, и умножить на 2. P = (a + b) · 2. ИЛИ Р = 2 · а + 2 · b. Стороны прямоугольника, которые лежат друг против друга (противолежащие), называются длиной и шириной.

«a» — длина прямоугольника, более длинная пара его сторон.

«b» — ширина прямоугольника, более короткая пара его сторон.

Пример задачи на подсчет периметра прямоугольника:

Вычислите периметр прямоугольника, есть его ширина равна 3 см., а длина — 6.

Запомни формулы вычисления периметра прямоугольника!

Полупериметр — это сумма одной длины и одной ширины.

• Полупериметр прямоугольника — когда выполняешь первое действие в скобках – (a+b) .
• Чтобы из полупериметра получить периметр, нужно его увеличить в 2 раза, т.е. умножить на 2.

Как найти площадь прямоугольника

Формула площади прямоугольника S= a*b

Если в условии известна длина одной стороны и длина диагонали, то площадь найти можно, используя в таких задачах, теорему Пифагора, она позволяет найти длину стороны прямоугольного треугольника если известны длины двух других сторон.

• : a 2 + b 2 = c 2 , где a и b – стороны треугольника, а с – гипотенуза, самая длинная сторона.

Помни!

1. Все квадраты – прямоугольники, но не все прямоугольники – квадраты. Так как:
   • Прямоугольник — это четырехугольник со всеми прямыми углами.
   • Квадрат — прямоугольник, у которого все стороны равны.
2. Если ты находишь площадь, ответ всегда будет в квадратных единицах (мм 2 , см 2 , м 2 , км 2 и т.д.)

Не многие формулы из курса школьной математики мы применяем в повседневной жизни. Однако, есть такие уравнения, которые имеют применение, если не на регулярной основе, то время от времени. Одна из таких формул — вычисление периметра фигуры.

Что такое периметр?

Периметром называют суммарную длину всех сторон геометрической фигуры. Для его обозначения используется буква латинского алфавита «Р». Проще говоря, чтобы найти периметр, необходимо измерить длины всех сторон геометрической фигуры и сложить полученные значения. Длина вычисляется обычным измерительным прибором, таким как линейка, рулетка, сантиметровая лента и прочее.

Единицей измерения соответственно являются сантиметры, метры, миллиметры и другие меры длины. Длина стороны многоугольника вычисляется путем прикладывания измерительного прибора от одной вершины к другой. Начало шкалы деления прибора должно совпадать с одной из вершин. Второе числовое значение, на которое попадает другая вершина и является длиной стороны многоугольника. Таким же образом необходимо измерить все длины сторон фигуры и полученные значения сложить. Единицей измерения периметра является та же самая единица, которая используется для измерения стороны фигуры.

Прямоугольником следует называть геометрическую фигуру, которая состоит из четырех сторон разной длины и три угла у которой прямые. При построении такой фигуры на плоскости получается так, что стороны у нее будут попарно равны, но не равны все между собой. Что такое периметр прямоугольника? Это также суммарная длина всех длин фигуры. Но так как у прямоугольника по две стороны имеют одинаковое значение, то в вычислении периметра можно дважды сложить длины двух смежных сторон. Единицей измерения периметра прямоугольника также являются общепринятые единицы измерения.

Треугольником следует называть геометрическую фигуру, имеющую три угла (как разного значения, так и одинакового) и состоящую из отрезков, образованных от точек пересечения лучей, образующих углы. Треугольник имеет три стороны и три угла. В нем могут быть из трех равны две стороны. Такой треугольник следует считать равнобедренным. Бывают такие фигуры, в которых равны все три стороны между собой. Принято такие треугольники называть равносторонними.

Что такое периметр треугольника? Его вычисление можно провести по аналогии с периметром четырехугольника. Равен периметр треугольника суммарной длине длин его сторон. Вычисление периметра треугольника, в котором две стороны равны — равнобедренного — упрощается умножением одной длины равных сторон на два. К полученному значению необходимо прибавить значение длины третьей стороны. Вычисление периметра треугольника с равными сторонами можно свести к простому вычислению произведения одной длины стороны треугольника на три.

Прикладное значение периметра

Вычисление периметра в повседневной жизни применяется во многих сферах, но чаще всего при выполнении строительных, геодезических, топографических, архитектурных, планировочных работах. Но перечисленным сферы применения вычисления периметра, конечно же, не ограничиваются.

Например, при выполнении геодезических и топографических работ очень часто возникает необходимость посчитать периметр границ определенного участка. Но на практике участки редко имеют правильную форму. Поэтому вычисление длины периметра происходит по формуле расчета суммы длин всех сторон участка.

Необходимость вычисления периметра участка очень часто обусловлена тем, что необходимо знать, какое количество материала потребуется для установки ограждений. Даже простой приусадебный участок нуждается в измерении периметра для того, чтобы грамотно обнести его забором.

Измерительные приборы на местности

Для вычисления периметра на местности невозможно использование простой ученической линейки. Поэтому специалисты используют специальные приборы. Конечно, самый простой и доступный вариант — это измерение длины границы участка шагами. Размер шага взрослого человека составляет примерно один метр. Иногда один метр и двадцать сантиметров. Но этот способ очень неточный и дает большую погрешность в измерении. Он подходит в том случае, если нет необходимости точного вычисления длины границы, а есть потребность просто прикинуть примерную длину.

Для более точного вычисления длины сторон участка и, соответственно, периметра, существуют специальные приборы. В первую очередь, можно воспользоваться специальной металлической рулеткой или обычным проводом.

Также существуют специальные измерительные устройства, такие как дальномеры. Приборы бывают оптические, лазерные, световые, ультразвуковые. Следует помнить, что чем дальше дальномер способен измерять расстояние, тем выше у него погрешность. Такие приборы используются в геодезических и топографических съемках.

Определение площади сложной фигуры с помощью теории вероятностей / Хабр

Зачем определять площадь сложной фигуры?

Да мало ли зачем. Например, возникла необходимость определить площадь территории на карте. Конечно, можно посмотреть в справочнике или поискать в интернете, но иногда и территории бывают нестандартными — допустим, вы озаботились проблемами лесов в пойме Амазонки и хотите ежемесячно измерять площадь зелёных пятен на фотографиях со спутника. Если вы ботаник (в хорошем смысле слова), то вам может понадобиться измерить площадь листовой поверхности разных сортов одного растения. Или, к примеру, более прозаичная задача — нужно зашпатлевать кусок стены, а банки шпатлёвки хватает только на 1 кв. м. — нужно выяснить, покупать одну банку или раскошелиться на две.

В чём сложность нахождения площади?

Конечно, если фигура представляет собой прямоугольник, круг или, что хуже, эллипс, то проблема решается с помощью Google и калькулятора. Но где бы найти формулу, да попроще, для нахождения площади, скажем, такого рисунка?

Теория вероятностей, Ваш выход!

Сразу оговорюсь, что теория вероятностей по своей сути не подразумевает точного решения задач. Так будет и в этом случае — если вам нужна космическая точность, то предлагаю копать в сторону методов имитационного моделирования. Если же погрешность в пределах 2-5% вас вполне устраивает, то будет достаточно того же калькулятора, базовых навыков программирования и умения считать до ста.

Суть метода

Суть метода проста до банальности. Допустим, мы пасмурным деньком выложили капустный листочек (см. ремарку про биолога выше) на прямоугольный поддон, а поддон выставили под накрапывающий дождик. А потом засекли определённое время (к примеру, пять минут) и посчитали, сколько капелек упало на поддон, а сколько непосредственно на лист. Если принять во внимание, что дождь обычно капает равномерно, то получается простая пропорция — лист во столько раз меньше поддона, во сколько раз на него упало меньше капель дождя, чем на весь поддон.

Возвращаемся к нашей фигуре

Итак, как же определить площадь той розовой пятерни? Да очень просто — заключить фигуру в прямоугольные границы и проставить случайным образом много точек. Чем больше, тем лучше (в соответствии с законом больших чисел). А потом подсчитать количество точек, попавших на фигуру.

Я намеренно не обсуждаю вопросы реализации такого алгоритма, потому что вариантов масса. Можно просто закрыть глаза и наугад тыкать шариковой ручкой, а можно действовать более научно — с помощью языков программирования. Например, код на PHP занял у меня не больше 15 строчек, а в результате получилось вот что:

Точки общим числом 300, разумеется, проставлены с помощью генератора случайных чисел. Для удобства подсчета точек я разбил изображение на 36 секторов — теперь нужно подсчитать количество точек, попавших на изображение, в каждом секторе, а результаты сложить. Сведём данные в таблицу (ячейка таблицы соответствует сектору на картинке):

0	4	8	4	0	0
0	7	5	6	0	4
3	6	13	7	8	5
1	10	10	13	7	2
0	2	3	7	10	2
0	0	2	5	3	0

Теперь у нас есть все данные для того, чтобы вычислить площадь розовой пятерни:
площадь описанного прямоугольника — 20 см х 20 см = 400 кв. см;
количество точек в прямоугольнике — 300;
количество точек внутри фигуры (сумма значений из таблицы) — 157;
площадь фигуры — 209,33 кв. см.

И насколько это точно?

Действительно, осталось определиться с точностью данного метода. Конечно, всё зависит от количества точек, и здесь нужно соблюдать золотую середину — десяти для нашего примера было бы явно недостаточно, а от тысячи слишком рябило бы в глазах. Поэтому попробуем определить погрешность для трёхсот точек и описанного квадрата со стороной 20 см. Для этого возьмём фигуру, площадь которой нам известна заранее. Например, такую:

Проставляем точки:

Результаты заносим в таблицу:

0	6	11	8	5	0
9	15	8	5	13	2
11	8	5	14	13	5
10	11	8	8	4	4
2	14	9	10	4	1
0	3	5	6	0	0

Рассчитываем площадь фигуры:
площадь описанного прямоугольника — 20 см х 20 см = 400 кв. см;
количество точек в прямоугольнике — 300;
количество точек внутри фигуры (сумма значений из таблицы) — 237;
площадь фигуры — 316 кв. см.

Нетрудно посчитать, что реальная площадь круга с радиусом 10 см составляет 314,16 кв. см. Таким образом, погрешность метода составила 0,59%, чего в большинстве случаев достаточно для прикладного использования.

Как найти площадь фигуры? Ответ на webmath.ru

Содержание:

Определения

Площадь является одним из основных математических понятий. Она характеризует как плоские, так и поверхностные геометрические объекты.

Определение

Площадью плоской замкнутой фигуры называется величина части плоскости, которая находится внутри указанной фигуры.

Единицей измерения площади плоской фигуры является квадрат со стороной, равной единице. Число, соответствующее площади некоторой фигуры, состоящей из частей, равно сумме чисел, соответствующих площадям этих частей. Измерение площадей треугольников и многоугольников основано на возможности построения равновеликих им прямоугольников.

Площадь произвольной ограниченной плоской фигуры определяется как общий предел площадей описанных и вписанных в нее многоугольников, наибольшие стороны которых по длине стремятся к нулю.

Если фигура имеет площадь, то она называется квадрируемой.

Формулы площади основных геометрических фигур

Площадь треугольника

Чтобы найти площадь треугольника, надо найти полупроизведение двух его сторон на синус угла между ними. То есть если известны длины двух сторон треугольника $ABC$, которые равны $a$ и $b$, а также угол $\alpha$ между этими сторонами, то искомая площадь:

$$\mathrm{S}_{\Delta A B C}=\frac{1}{2} a b \sin \alpha$$

Читать дальше: формулы площади треугольника и примеры решений →

Площадь круга

Чтобы найти площадь круга, надо найти произведение числа $\pi$ на квадрат радиуса этого круга, то есть

$$\mathrm{S}_{\kappa p}=\pi R^{2}$$

Читать дальше: формула площади круга и примеры решений →

Площадь квадрата

Чтобы найти площадь квадрата, надо длину его стороны возвести в квадрат, то есть

Читать дальше: формула площади квадрата и примеры решений →

Площадь прямоугольника

Чтобы найти площадь прямоугольника, надо его длину умножить на ширину, то есть

Читать дальше: формула площади прямоугольника и примеры решений →

Площадь параллелограмма

Чтобы найти площадь параллелограмма, нужно найти произведение стороны $a$ параллелограмма на высоту , проведенную к этой стороне, то есть

Читать дальше: формулы площади параллелограмма и примеры решений →

Площадь трапеции

Чтобы найти площадь трапеции, нужно длину средней линии умножить на длину высоты , опущенной к основанию:

Читать дальше: формулы площади трапеции и примеры решений →

Площадь ромба

Чтобы найти площадь ромба, надо длину стороны умножить на длину высоты, проведенной к этой стороне:

Читать дальше: формулы площади ромба и примеры решений →

Площадь эллипса

Чтобы найти площадь эллипса, нужно найти произведение длин большой и малой полуосей этого эллипса на число $\pi$, то есть

Читать дальше: формула площади эллипса и примеры решений →

Площадь по периметру калькулятор. Как вычислить площадь по периметру. К разным фигурам применяйте различные формулы

Геометрия постигает свойства и колляции двумерных и пространственных фигур. Числовыми величинами, характеризующими такие конструкции, являются площадь и периметр, вычисление которых производится по знаменитым формулам либо выражается одно через другое.

Инструкция

1. Прямоугольник.Задача: вычислите площадь прямоугольника, если вестимо, что его периметр равен 40, а длина b в 1,5 раза огромнее ширины a.

2. Решение.Используйте знаменитую формулу периметра, он равен сумме всех сторон фигуры. В данном случае P = 2 a + 2 b. Из исходных данных задачи вы знаете, что b = 1,5 a, следственно, P = 2 a + 2 1,5 a = 5 a, откуда a = 8. Обнаружьте длину b = 1,5 8 = 12.

3. Запишите формулу для площади прямоугольника:S = a b,Подставьте вестимые величины:S = 8 *12 = 96.

4. Квадрат.Задача: обнаружьте площадь квадрата, если периметр равен 36.

5. Решение.Квадрат – частный случай прямоугольника, где все стороны равны, следственно, его периметр равен 4 a, откуда a = 8. Площадь квадрата определите по формуле S = a? = 64.

6. Треугольник.Задача: пускай дан произвольный треугольник ABC, периметр которого равен 29. Узнайте величину его площади, если знаменито, что высота BH, опущенная на сторону AC, делит ее на отрезки с длинами 3 и 4 см.

7. Решение.Для начала припомните формулу площади для треугольника:S = 1/2 c h, где c – основание и h – высота фигуры. В нашем случае основанием будет сторона AC, которая знаменита по условию задачи: AC = 3+4 = 7, осталось обнаружить высоту BH.

8. Высота является перпендикуляром, проведенным к стороне из противоположной вершины, следственно, она разделять треугольник ABC на два прямоугольных треугольника. Зная это качество, разглядите треугольник ABH. Припомните формулу Пифагора, согласно которой:AB? = BH? + AH? = BH? + 9 ? AB = ?(h? + 9).В треугольнике BHC по тому же тезису запишите:BC? = BH? + HC? = BH? + 16 ? BC = ?(h? + 16).

9. Примените формулу периметра:P = AB + BC + ACПодставьте величины, выраженные через высоту:P = 29 = ?(h? + 9) + ?(h? + 16) + 7.

10. Решите уравнение:?(h? + 9) + ?(h? + 16) = 22 ? [замена t? = h? + 9]:?(t? + 7) = 22 – t, возведите обе стороны равенства в квадрат:t? + 7 = 484 – 44 t + t? ? t?10,84h? + 9 = 117,5 ? h ? 10,42

11. Обнаружьте площадь треугольника ABC:S = 1/2 7 10,42 = 36,47.

При решении, необходимо принять во внимание, что решить задачу о нахождении площади прямоугольника только из длины его сторон нельзя .

В этом несложно убедиться. Пусть периметр прямоугольника будет равен 20 см. Это будет верно, если его стороны 1 и 9, 2 и 8, 3 и 7 см. Все эти три прямоугольника будут иметь одинаковый периметр, равный двадцати сантиметрам. (1 + 9) * 2 = 20 точно также как и (2 + 8) * 2 = 20 см.
Как видно, мы можем подобрать бесконечное количество вариантов размеров сторон прямоугольника, периметр которого будет равен заданному значению.

Площадь прямоугольников с заданным периметром 20 см, но с различными сторонами будет различна. Для приведенного примера — 9, 16 и 21 квадратных сантиметров соответственно.
S 1 = 1 * 9 = 9 см 2
S 2 = 2 * 8 = 16 см 2
S 3 = 3 * 7 = 21 см 2
Как видим, вариантов площади фигуры при заданном периметре — бесконечное количество.

Замечание для любознательных . В случае с прямоугольником, у которого задан периметр, максимальную площадь будет иметь квадрат.

Таким образом, для того, чтобы вычислить площадь прямоугольника из его периметра, нужно обязательно знать либо соотношение его сторон, либо длину одной из них. Единственной фигурой, которая имеет однозначную зависимость своей площади от периметра, является круг. Только для круга и возможно решение.

В этом уроке:

• Задача 4. Изменение длины сторон при сохранении площади прямоугольника

Задача 1. Найти стороны прямоугольника из площади

Периметр прямоугольника равен 32 сантиметрам, а сумма площадей квадратов, построенных на каждой из его сторон — 260 квадратных сантиметров. Найдите стороны прямоугольника.
Решение.

2(x+y)=32
Согласно условию задачи, сумма площадей квадратов построенных на каждой из его сторон (квадратов, соответственно, четыре) будет равна
2x 2 +2y 2 =260
x+y=16
x=16-y
2(16-y) 2 +2y 2 =260
2(256-32y+y 2)+2y 2 =260
512-64y+4y 2 -260=0
4y 2 -64y+252=0
D=4096-16×252=64
x 1 =9
x 2 =7
Теперь примем во внимание, что исходя из того, что x+y=16 (см. выше) при x=9, то y=7 и наоборот, если x=7, то y=9
Ответ : Стороны прямоугольника равны 7 и 9 сантиметров

Задача 2. Найти стороны прямоугольника из периметра

Периметр прямоугольника 26 см, а сумма площадей квадратов, построенных на двух его смежных сторонах, равна 89 кв. см. Найдите стороны прямоугольника.
Решение.
Обозначим стороны прямоугольника как x и y.
Тогда периметр прямоугольника равен:
2(x+y)=26
Сумма площадей квадратов построенных на каждой из его сторон (квадратов, соответственно, два и это квадраты ширины и высоты, поскольку стороны смежные) будет равна
x 2 +y 2 =89
Решаем полученную систему уравнений. Из первого уравнения выводим, что
x+y=13
y=13-y
Теперь выполняем подстановку во второе уравнение, заменяя x его эквивалентом.
(13-y) 2 +y 2 =89
169-26y+y 2 +y 2 -89=0
2y 2 -26y+80=0
Решаем полученное квадратное уравнение.
D=676-640=36
x 1 =5
x 2 =8
Теперь примем во внимание, что исходя из того, что x+y=13 (см. выше) при x=5, то y=8 и наоборот, если x=8, то y=5
Ответ: 5 и 8 см

Задача 3. Найти площадь прямоугольника из пропорции его сторон

Найти площадь прямоугольника если его периметр равен 26 см а стороны пропорциональны как 2 к 3.

Решение.
Обозначим стороны прямоугольника через коэффициент пропорциональности x.
Откуда длина одной стороны будет равна 2x, другой — 3х.

Тогда:
2(2x+3x)=26
2x+3x=13
5x=13
x=13/5
Теперь, исходя из полученных данных, определим площадь прямоугольника:
2x*3x=2*13/5*3*13/5=40,56 см 2

Задача 4 . Изменение длины сторон при сохранении площади прямоугольника Длина прямоугольника увеличена на 25%. На сколько процентов надо уменьшить ширину, чтобы его площадь не изменилась?

Решение .
Площадь прямоугольника равна
S = ab

В нашем случае один из множителей увеличился на 25%, что означает a 2 = 1,25a . Таким образом, новая площадь прямоугольника должна быть равна
S 2 = 1,25ab

Таким образом, для того, чтобы вернуть площадь прямоугольника к начальному значению, то
S 2 = S / 1.25
S 2 = 1,25ab / 1.25

Поскольку новый размер а изменять нельзя, то
S 2 = (1,25a) b / 1.25

1 / 1,25 = 0,8
Таким образом, величину второй стороны нужно уменьшить на (1 — 0,8) * 100% = 20%

Ответ : ширину нужно уменьшить на 20%.

Определение периметра и площади геометрических фигур — важная задача, которая возникает при решении многих практических или бытовых задач. Если вам требуется поклеить обои, установить забор, рассчитать расход краски или кафеля, то вам обязательно придется иметь дело с геометрическими расчетами.

Для решения перечисленных бытовых вопросов вам потребуется работать с самыми разными геометрическими фигурами. Мы представляем вам каталог онлайн-калькуляторов, которые позволяют вычислить параметры наиболее популярных плоских фигур. Рассмотрим их.

Круг

Частные случаи

Четырехугольник с одинаковыми сторонами. Параллелограмм становится ромбом в случаях, если его диагонали пересекаются под углом 90 градусов и являются биссектрисами своих углов.

Это параллелограмм с прямыми углами. Кроме того, параллелограмм считается прямоугольником, если его стороны и диагонали отвечают условиям теоремы Пифагора.

Это параллелограмм, у которого все стороны равны и все углы равны. Диагонали квадрата полностью повторяют свойства диагоналей прямоугольника и ромба, что делает квадрат уникальной фигурой, которая характеризуется максимальной симметрией.

Многоугольник

Правильный полигон — это выпуклая фигура на плоскости, которая имеет равные стороны и равные углы. В зависимости от количества сторон многоугольники имеют собственные названия:

• — пентагон;
• — гексагон;
• восемь — октагон;
• двенадцать — додекагон.

И так далее. Геометры шутят, что круг — это многоугольник с бесконечным количеством углов. Наш калькулятор запрограммирован на определение периметров и площадей только правильных многоугольников. Он использует общие формулы для всех правильных полигонов. Для вычисления периметра используется формула:

где n – количество сторон многоугольника, a – длина стороны.

Для определения площади используется выражение:

S = n/4 × a 2 × ctg(pi/n).

Подставляя соответствующее n, мы можем подобрать формулу для любого правильного многоугольника, к которым также относятся равносторонний треугольник и квадрат.

Многоугольники имеют большое распространение в реальной жизни. Так форму пятиугольника имеет здание министерства обороны США — Пентагон, гексагона — пчелиные соты или кристаллы снежинки, октагона — дорожные знаки. Кроме того, многие простейшие, например радиолярии, имеют форму правильных полигонов.

Примеры из реальной жизни

Давайте рассмотрим пару примеров использования нашего калькулятора в реальных расчетах.

Покраска забора

Покраска поверхностей и расчет краски — это одни из самых очевидных бытовых задач, в которых требуются минимальные математические расчеты. Если нам нужно покрасить забор, высота которого составляет 1,5 метра, а длина 20 метров, то сколько потребуется банок краски? Для этого нужно узнать суммарную площадь забора и расход лакокрасочных материалов на 1 квадратный метр. Мы знаем, что расход эмали составляет 130 грамм на метр. Теперь определим площадь забора, используя калькулятор для вычисления площади прямоугольника. Она составит S = 30 квадратных метров. Естественно, что забор мы будем красить с обеих сторон, поэтому площадь для покраски увеличится до 60 квадратов. Тогда нам понадобится 60 × 0,13 = 7,8 килограмм краски или три стандартных банки по 2,8 килограмма.

Отделка бахромой

Пошив одежды — еще одна отрасль, в которой необходимы обширные геометрические познания. Пусть нам надо отделать бахромой платок, который представляет собой равнобедренную трапецию со сторонами 150, 100, 75 и 75 см. Для вычисления расхода бахромы нам потребуется узнать периметр трапеции. В этом нам и пригодится онлайн-калькулятор. Введем эти данные ячейки и получим ответ:

Таким образом, нам понадобится 4 м бахромы для отделки платка.

Заключение

Плоские фигуры составляют реальный мир вокруг. Мы часто задавались в школе вопросом, пригодится ли нам геометрия в будущем? Выше приведенные примеры показывают, что математика постоянно используется в повседневной жизни. И если площадь прямоугольника для нас привычна, то вычислить площадь додекагона может оказаться трудной задачей. Используйте наш каталог калькуляторов для решения школьных заданий или бытовых вопросов.

Как вычислить площадь фигуры зная ее периметр? и получил лучший ответ

Ответ от Ёемен Аркадьевич[гуру]
В Компас 3D нанести план и автоматически посчитать площадь. По периметру площадь произвольного многоугольника не посчитать. Все равно придется разбивать на отдельные фигуры.
Будут вопросы — пиши в агент.

Ответ от Ѐамис Ш [новичек]
..

Ответ от Kiss(RUSS фор всех) ки (я) [гуру]
1.выбрать центр
2.измерить расстояние от центра до углов
3.измерить стороны вашего многоугольника
4.вычислить периметры получившихся N треугольников
5.вычислить площади всех треугольников, используя формулу Герона-через полупериметр.
6.суммировать все площади
7.выбрать мой ответ лучшим.
8.все

Ответ от Semrid [гуру]
попробуй разделить периметр на 4 и потом перемножить полученное друг на друга

Ответ от ScrAll [гуру]
Вырезаешь из бумаги и взвешиваешь.
Или разбиваешь на треугольники.
Половина основания на высоту…

Ответ от Алексей Зайцев [гуру]
Проще и безошибочнее начертить эскизик — вид сверху с размерами. Затем по этому эскизику площадь разделить на прямоугольники, посчитать и просуммировать их площади

Ответ от Мария Кемпель [активный]
нереально

Ответ от Nemo [гуру]
Нереально. По периметру вычисляется площадь только ПРАВИЛЬНЫХ фигур. Советую кусочным способом

Ответ от Djon [гуру]
лучше всего разбить сложную фигуру на несколько простых, и посчитать площадь отдельно, затем сложить

Ответ от Lavavoth [гуру]
Нереально.. . Лучше выложи план зала, есть другие способы подсчета, но нужно видеть план.

Ответ от 3 ответа [гуру]

Привет! Вот подборка тем с ответами на Ваш вопрос: Как вычислить площадь фигуры зная ее периметр?

Петя хочет нарисовать фигуру, у которой периметр 12 см, а площадь 12 кв. см. Докажите, что у него ничего не получится
максимальная площадь по периметру у фигуры — Круг.
Если площадь круга с длинной окружности 12

Как рассчитать площадь многоугольника зная периметр. Как найти площадь многоугольника? Теорема: площадь прямоугольника

Каждый, кто изучал в школе математику и геометрию, хотя бы поверхностно знает эти науки. Но со временем, если в них не практиковаться, познания забываются. Многие даже считают, что только зря потратили своё время, изучая геометрические расчёты. Однако они ошибаются. Технические работники выполняют повседневную работу, связанную с геометрическими расчётами. Что касается расчета площади многоугольника, то и эти знания находят своё применение в жизни. Понадобятся они хотя бы для того, чтобы рассчитать площадь земельного участка. Итак, давайте узнаем, как найти площадь многоугольника.

Определение многоугольника

Сначала определимся с тем, что такое многоугольник. Это плоская геометрическая фигура, которая образовалась в результате пересечения трех или более прямых. Другое простое определение: многоугольник — это замкнутая ломаная. Естественно, при пересечении прямых образуются точки пересечения, их количество равно количеству прямых, образовывающих многоугольник. Точки пересечения называют вершинами, а отрезки, образованные от прямых, — сторонами многоугольника. Смежные отрезки многоугольника находятся не на одной прямой. Отрезки, являющиеся несмежными, — это те, которые не проходят через общие точки.

Сумма площадей треугольников

Как находить площадь многоугольника? Площадь многоугольника — это внутренняя часть плоскости, которая образовалась при пересечении отрезков или сторон многоугольника. Поскольку многоугольник — это сочетание таких фигур, как треугольник, ромб, квадрат, трапеция, то универсальной формулы для вычисления его площади просто нет. На практике наиболее универсальным является метод разбиения многоугольника на более простые фигуры, нахождение площади которых не вызывают затруднений. Сложив суммы площадей этих простых фигур, получают площадь многоугольника.

Через площадь окружности

В большинстве случаев многоугольник имеет правильную форму и образует фигуру с равными сторонами и углами между ними. Рассчитать площадь в этом случае очень просто при помощи вписанной или описанной окружности. Если известна площадь окружности, то её необходимо умножить на периметр многоугольника, а затем полученное произведение поделить на 2. В итоге получается формула расчёта площади такого многоугольника: S = ½∙P∙r., где P — площадь окружности, а r — периметр многоугольника.

Метод разбиения многоугольника на «удобные» фигуры — самый популярный в геометрии, он позволяет быстро и правильно найти площадь многоугольника. 4 класс средней школы обычно изучает такие методы.

Тема «Площади многоугольников» является неотъемлемой частью школьного курса математики, что вполне естественно. Ведь исторически само возникновение геометрии связано с потребностью сравнения земельных участков той или иной формы. Вместе с тем следует отметить, что образовательные возможности раскрытия этой темы в средней школе используются далеко не полностью.

Основная задача обучения математике в школе заключается в обеспечении прочного и сознательного овладения учащимися системой математических знаний и умений, необходимых в повседневной жизни и трудовой деятельности каждому члену современного общества, достаточных для изучения смежных дисциплин и продолжения образования.

Наряду с решением основной задачи углубленное изучение математики предусматривает формирование у учащихся устойчивого интереса к предмету, выявление и развитие их математических способностей, ориентацию на профессии, существенным образом связанные с математикой, подготовку к обучению в вузе.

Квалификационная работа включает содержание курса математики общеобразовательной школы и ряд дополнительных вопросов, непосредственно примыкающих к этому курсу и углубляющих его по основным идейным линиям.

Включение дополнительных вопросов преследует две взаимосвязанные цели. С одной стороны, это создание в совокупности с основными разделами курса базы для удовлетворения интересов и развития способностей учащихся, имеющих склонность к математике, с другой – выполнение содержательных пробелов основного курса, придающее содержанию углубленного изучения необходимую целостность.

Квалификационная работа состоит из введения, двух глав, заключения и цитируемой литературы. В первой главе рассматриваются теоретические основы изучения площадей многоугольников, а во второй главе – непосредственно уже методические особенности изучения площадей.

1.1Вычисление площадей в древности

Зачатки геометрических знаний, связанных с измерением площадей, теряются в глубине тысячелетий.

Еще в 4 – 5 тысяч лет назад вавилоняне умели определять площадь прямоугольника и трапеции в квадратных единицах. Квадрат издавна служит эталоном при измерении площадей благодаря многим своим замечательным свойствам: равные стороны, равные и прямые углы, симметричность и общее совершенство формы. Квадраты легко строить, или можно заполнить плоскость без пробелов.

В древнем Китае мерой площади был прямоугольник. Когда каменщики определяли площадь прямоугольной стены дома, они перемножали высоту и ширину стены. Таково принятое в геометрии определение: площадь прямоугольника равна произведению его смежных сторон. Обе эти стороны должны быть выражены в одних и тех же линейных единицах. Их произведение и составит площадь прямоугольника, выраженную в соответствующих квадратных единицах. Скажем, если высота и ширина стены измерены в дециметрах, то произведение обоих измерений будет выражено в квадратных дециметрах. И если площадь каждой облицовочной Плотки составляет квадратный дециметр, то полученное произведение укажет число плиток, нужное для облицовки. Это вытекает из утверждения, положенного в основу измерения площадей: площадь фигуры, составленной из непересекающихся фигур, равна сумме их площадей.

Древние египтяне 4000 лет назад пользовались почти теми же приемами, что и мы, для измерения площади прямоугольника, треугольника и трапеции: основание треугольника делилось пополам, и умножалась на высоту; для трапеции же сумма параллельных сторон делилась пополам и умножалась на высоту и т.п. Для вычисления площади

четырехугольника со сторонами (рис. 1.1) применялась формула (1.1)

т.е. умножались полусуммы противоположных сторон.

Эта формула явно неверна для любого четырехугольника, из нее вытекает, в частности, что площади всех ромбов одинаковы. Между тем, очевидно, что у таких ромбов площади зависят от величины углов при вершинах. Данная формула верна только для прямоугольника. С ее помощью можно вычислить приближенно площадь четырехугольников, у которых углы близки к прямым.

Для определения площади

равнобедренного треугольника (рис. 1.2), в котором , египтяне пользовались приближенной формулой:
(1.2) Рис. 1.2Совершаемая при этом ошибка тем меньше, чем меньше разность между стороной и высотой треугольника, иными словами, чем ближе вершина (и ) к основанию высоты из . Вот почему приближенная формула (1.2) применима лишь для треугольников с сравнительно малым углом при вершине.

Но уже древние греки умели правильно находить площади многоугольников. В своих «Началах» Евклид не употребляет слова «площадь», так как он под самим словом «фигура» понимает часть плоскости, ограниченную той или иной замкнутой линией. Евклид не выражает результат измерения площади числом, а сравнивает площади разных фигур между собой.

Как и другие ученые древности, Евклид занимается вопросами превращения одних фигур в другие, им равновеликие. Площадь составной фигуры не изменится, если ее части расположить по-другому, но без пересечения. Поэтому, например, можно, исходя из формул площади прямоугольника, находить формулы площадей других фигур. Так, треугольник разбивается на такие части, из которых затем можно составить равновеликий ему прямоугольник. Из этого построения следует, что площадь треугольника равна половине произведения его основания на высоту. Прибегая к подобной перекройке, находят, что площадь параллелограмма равна произведению основания на высоту, площадь трапеции – произведению полусуммы оснований на высоту.

Когда каменщикам приходится облицовывать стену сложной конфигурации, они могут определить площадь стены, подсчитав число пошедших на облицовку плиток. Некоторые плитки, естественно, придется обкалывать, чтобы края облицовки совпали с кромкой стены. Число всех пошедших в работу плиток оценивает площадь стены с избытком, число необломанных плиток – с недостатком. С уменьшением размеров клеток количество отходов уменьшается, и площадь стены, определяемая через число плиток, вычисляется все точнее.

Одним из поздних греческих математиков – энциклопедистов, труды которого имели главным образом прикладной характер, был Герон Александрийский, живший в 1 в. н. э. Будучи выдающимся инженером, он был назван также «Герон Механик». В своем произведении «Диоптрика» Герон описывает разные машины и практические измерительные инструменты.

Одна из книг Герона была названа им «Геометрика» и является своего рода сборником формул и соответствующих задач. Она содержит примеры на вычисление площадей квадратов, прямоугольников и треугольников. О нахождении площади треугольника по его сторонам Герон пишет: « Пусть, например, одна сторона треугольника имеет в длину 13 мерных шнуров, вторая 14 и третья 15. Чтобы найти площадь, поступают вот как. Сложи 13, 14 и 15; получится 42. Половина этого будет 21. Вычти из этого три стороны одну за другой; сперва вычти 13 – останется 8, затем 14 – останется 7 и, наконец, 15 – останется 6. А теперь перемножь их: 21раз по 8 даст 168, возьми это 7 раз – получится 1176, а это еще 6 раз – получится 7056. Отсюда квадратный корень будет 84. Вот сколько мерных шнуров будет в площади треугольника».

• обучающие: научить учащихся находить площадь многоугольника, используя выбранные ими способы, сформировать начальные представления
• многоугольнике, графические и измерительные навыки;
• развивающие: развитие способов умственной деятельности учащихся при выполнении заданий от наблюдения, расчетов до выяснения закономерностей вычисления площади многоугольника;
• воспитывающие: раскрытие субъективного опыта учащихся, поощрение действий, стремлений учащихся как основы воспитания положительных качеств личности;
• методическая: создание условий для проявления познавательной активности учащихся.

Оснащение урока:

1. Оформление доски: слева — фигуры многоугольника, справа — чистое полотно доски для записи на уроке, в центре – многоугольник-прямоугольник.
2. Листок “К исследованию”.
3. Инструментарии учителя и учащихся (мел, указка, линейка, листок исследования, фигуры, ватман, маркер).

Метод урока:

• По взаимодействию учителя и учащихся – диалог-общение;
• По способу решения задач – частично-поисковый;
• По способу умственной деятельности — (СУД) развивающее обучение.

Форма урока — фронтальная, в парах, индивидуальная.

Тип урока — урок усвоения новых знаний, умений и навыков.

Структура урока — постепенное углубление в тему, гибкая, диалогическая.

Ход урока

Приветствие.

Урок прекрасен и приносит радость, когда мы мыслим, дружно работаем. Сегодня мы будем рассматривать фигуры, определять их названия, думать, искать и находить решения. Пожелаем друг другу успешной работы.

Актуализация знаний.

Рассмотрите фигуры (на доске многоугольники).

Они все вместе. Почему? Какой у них общий признак? (Многоугольники).

Назовите этот многоугольник (5-угольник, 6-угольник…)

Может быть, вы знаете, что такое площадь многоугольника?

Тогда покажите на одной из фигур.

(Обобщение учителем: площадь — часть плоскости внутри замкнутой геометрической фигуры.)

В русском языке это слово имеет несколько значений.

(Ученик по словарю знакомит со значениями.)

1. Часть плоскости внутри замкнутой геометрической фигуры.
2. Большое незастроенное и ровное место.
3. Помещение для какой-либо цели.

Какое из значений используется в математике?

В математике используется первое значение.

(На доске фигура).

Это многоугольник? Да.

Назовите фигуру по-другому. Прямоугольник.

Покажи длину, ширину.

Как найти площадь многоугольника?

Запишите при помощи букв и знаков формулу.

Если длина нашего прямоугольника 20 см, ширина 10см. Чему равна площадь?

Площадь равна 200 см 2

Подумайте, как приложить линейку, чтобы фигура разделилась на:

Увидели, из каких частей состоит фигура? А теперь, наоборот, по частям соберем целое.

(Части фигуры лежат на партах. Дети собирают из них прямоугольник).

Сделайте вывод по наблюдениям.

Целую фигуру можно разделить на части и из частей составить целую.

Дома на основе треугольников и четырехугольников составляли фигуры, силуэты. Вот какие они получились.

(Демонстрация рисунков, выполненных дома учащимися. Одна из работ анализируется).

Какие фигуры использовал? У тебя получился сложный многоугольник.

Постановка учебной задачи.

На уроке мы должны ответить на вопрос: как найти площадь сложного многоугольника?

Для чего человеку нужно находить площадь?

(Ответы детей и обобщение учителем).

Задача определения площади возникла из практики.

(Показывается план школьного участка).

Для того чтобы построить школу, сначала создали план. Потом разбивалась территория на участки определенной площади, размещались строения, клумбы, стадион. При этом участок имеет определенную форму — форму многоугольника.

Решение учебной задачи.

(Раздаются листы для исследования).

Перед вами фигура. Назовите ее.

Многоугольник, шестиугольник.

Найдем площадь многоугольника. Что для этого надо делать?

Разделить на прямоугольники.

(При затруднении будет другой вопрос: “Из каких фигур состоит многоугольник?”).

Из двух прямоугольников.

С помощью линейки и карандаша разделите фигуру на прямоугольники. Обозначьте цифрами 1 и 2 полученные части.

Проведем измерения.

Найдем площадь первой фигуры.

(Учащиеся предлагают следующие варианты решений и записывают их на доске).

• S 1 = 5 ? 2 = 10 см 2
• S 2 = 5 ? 1 = 5 см 2

Зная площадь частей, как найти площадь целой фигуры?

S = 10 + 5 = 15 см 2

• S 1 = 6 ? 2 = 12 см 2
• S 2 = 3 ? 1 = 3 см 2
• S = 12 + 3 = 15 см 2 .

Сравните результаты и сделайте вывод.

Проследим наши действия

Как находили площадь многоугольника?

Составляется и записывается на плакате алгоритм:?

1. Делим фигуру на части

2. Находим площади частей этих многоугольников (S 1 , S 2).

3. Находим площадь целого многоугольника (S 1 + S 2).

Проговорить алгоритм.

(Несколько учащихся проговаривают алгоритм).

Мы нашли два способа, а может, есть еще?

А можно фигуру достроить.

Сколько прямоугольников получилось?

Обозначим части 1 и 2. Проведем измерения.

Найдите площадь каждой части многоугольника.

• S 1= 6? 5=30см 2
• S 2 = 5 ? 3 = 15 см 2

Как найти площадь нашего шестиугольника?

S = 30 – 15 = 15 см 2

Составим алгоритм:

Достроили фигуру до прямоугольника

Нашли S 1 и S 2 .

Нашли разность S 1 – S 2 .

Сравните два алгоритма. Сделайте вывод. Какие действия одинаковые? Где разошлись наши действия?

Закройте глазки, опустите головки. Мысленно повторите алгоритм.

Мы провели исследовательскую работу, рассмотрели разные способы и теперь можем находить площадь любого многоугольника.

Проверка результативности.

Проверьте себя.

Перед вами многоугольники.

Найти площадь одной фигуры по выбору, при этом можете пользоваться разными способами.

Работа выполняется самостоятельно. Дети выбирают фигуру. Находят площадь одним из способов. Проверка – ключ на доске.

Что можно сказать о форме? (Форма разная)

А какова площадь этих многоугольников? (Площади этих многоугольников равны)

Оценивают результаты.

У кого правильно – поставь “+”.

У кого сомнения, затруднения – “?”

Консультанты оказывают помощь ребятам, ищут ошибки, помогают исправить.

Домашнее задание:

Составить свои листки исследования, вычислить площадь многоугольника разными способами.

Итог урока.

Итак, ребята, что вы расскажите родителям, о том как найти площадь геометрической фигуры – многоугольника.2 \Rightarrow S_{\text{пр-к}}=ab \end{multline*}\)

Определение

Высота параллелограмма — это перпендикуляр, проведенный из вершины параллелограмма к стороне (или к продолжению стороны), не содержащей эту вершину.
Например, высота \(BK\) падает на сторону \(AD\) , а высота \(BH\) — на продолжение стороны \(CD\) :

Теорема: площадь параллелограмма

Площадь параллелограмма равна произведению высоты и стороны, к которой проведена эта высота.

Доказательство

Проведем перпендикуляры \(AB»\) и \(DC»\) , как показано на рисунке. Заметим,что эти перпендикуляры равны высоте параллелограмма \(ABCD\) .

Тогда \(AB»C»D\) – прямоугольник, следовательно, \(S_{AB»C»D}=AB»\cdot AD\) .

Заметим, что прямоугольные треугольники \(ABB»\) и \(DCC»\) равны. Таким образом,

\(S_{ABCD}=S_{ABC»D}+S_{DCC»}=S_{ABC»D}+S_{ABB»}=S_{AB»C»D}=AB»\cdot AD.\)

\[{\Large{\text{Площадь треугольника}}}\]

Определение

Будем называть сторону, к которой в треугольнике проведена высота, основанием треугольника.

Теорема

Площадь треугольника равна половине произведения его основания на высоту, проведенную к этому основанию.

Доказательство

Пусть \(S\) – площадь треугольника \(ABC\) . Примем сторону \(AB\) за основание треугольника и проведём высоту \(CH\) . Докажем, что \ Достроим треугольник \(ABC\) до параллелограмма \(ABDC\) так, как показано на рисунке:

Треугольники \(ABC\) и \(DCB\) равны по трем сторонам (\(BC\) – их общая сторона, \(AB = CD\) и \(AC = BD\) как противоположные стороны параллелограмма \(ABDC\) ), поэтому их площади равны. Следовательно, площадь \(S\) треугольника \(ABC\) равна половине площади параллелограмма \(ABDC\) , то есть \(S = \dfrac{1}{2}AB\cdot CH\) .

Теорема

Если два треугольника \(\triangle ABC\) и \(\triangle A_1B_1C_1\) имеют равные высоты, то их площади относятся как основания, к которым эти высоты проведены.

Следствие

Медиана треугольника делит его на два треугольника, равных по площади.

Теорема

Если два треугольника \(\triangle ABC\) и \(\triangle A_2B_2C_2\) имеют по равному углу, то их площади относятся как произведения сторон, образующих этот угол.

Доказательство

Пусть \(\angle A=\angle A_2\) . Совместим эти углы так, как показано на рисунке (точка \(A\) совместилась с точкой \(A_2\) ):

Проведем высоты \(BH\) и \(C_2K\) .

Треугольники \(AB_2C_2\) и \(ABC_2\) имеют одинаковую высоту \(C_2K\) , следовательно: \[\dfrac{S_{AB_2C_2}}{S_{ABC_2}}=\dfrac{AB_2}{AB}\]

Треугольники \(ABC_2\) и \(ABC\) имеют одинаковую высоту \(BH\) , следовательно: \[\dfrac{S_{ABC_2}}{S_{ABC}}=\dfrac{AC_2}{AC}\]

Перемножая последние два равенства, получим: \[\dfrac{S_{AB_2C_2}}{S_{ABC}}=\dfrac{AB_2\cdot AC_2}{AB\cdot AC} \qquad \text{ или } \qquad \dfrac{S_{A_2B_2C_2}}{S_{ABC}}=\dfrac{A_2B_2\cdot A_2C_2}{AB\cdot AC}\]

Теорема Пифагора

В прямоугольном треугольнике квадрат длины гипотенузы равен сумме квадратов длин катетов:

Верно и обратное: если в треугольнике квадрат длины одной стороны равен сумме квадратов длин других двух сторон, то такой треугольник прямоугольный.

Теорема

Площадь прямоугольного треугольника равна половине произведения катетов.

Теорема: формула Герона

Пусть \(p\) – полупериметр треугольника, \(a\) , \(b\) , \(c\) – длины его сторон, тогда его площадь равна \

\[{\Large{\text{Площадь ромба и трапеции}}}\]

Замечание

Т.к. ромб является параллелограммом, то для него верна та же формула, т.е. площадь ромба равна произведению высоты и стороны, к которой проведена эта высота.

Теорема

Площадь выпуклого четырехугольника, диагонали которого перпендикулярны, равна половине произведения диагоналей.

Доказательство

Рассмотрим четырехугольник \(ABCD\) . Обозначим \(AO=a, CO=b, BO=x, DO=y\) :

Заметим, что данный четырехугольник составлен из четырех прямоугольных треугольников, следовательно, его площадь равна сумме площадей этих треугольников:

\(\begin{multline*} S_{ABCD}=\frac12ax+\frac12xb+\frac12by+\frac12ay=\frac12(ax+xb+by+ay)=\\ \frac12((a+b)x+(a+b)y)=\frac12(a+b)(x+y)\end{multline*}\)

Следствие: площадь ромба

Площадь ромба равна половине произведения его диагоналей: \

Определение

Высота трапеции – это перпендикуляр, проведенный из вершины одного основания к другому основанию.

Теорема: площадь трапеции

Площадь трапеции равна произведению полусуммы оснований на высоту.

Доказательство

Рассмотрим трапецию \(ABCD\) с основаниями \(BC\) и \(AD\) . Проведем \(CD»\parallel AB\) , как показано на рисунке:

Тогда \(ABCD»\) – параллелограмм.

Проведем также \(BH»\perp AD, CH\perp AD\) (\(BH»=CH\) – высоты трапеции).

Тогда \(S_{ABCD»}=BH»\cdot AD»=BH»\cdot BC, \quad S_{CDD»}=\dfrac12CH\cdot D»D\)

Т.к. трапеция состоит из параллелограмма \(ABCD»\) и треугольника \(CDD»\) , то ее площадь равна сумме площадей параллелограмма и треугольника, то есть:

\ \[=\dfrac12 CH\left(BC+AD»+D»D\right)=\dfrac12 CH\left(BC+AD\right)\]

• обучающие: научить учащихся находить площадь многоугольника, используя выбранные ими способы, сформировать начальные представления
• многоугольнике, графические и измерительные навыки;
• развивающие: развитие способов умственной деятельности учащихся при выполнении заданий от наблюдения, расчетов до выяснения закономерностей вычисления площади многоугольника;
• воспитывающие: раскрытие субъективного опыта учащихся, поощрение действий, стремлений учащихся как основы воспитания положительных качеств личности;
• методическая: создание условий для проявления познавательной активности учащихся.

Оснащение урока:

1. Оформление доски: слева — фигуры многоугольника, справа — чистое полотно доски для записи на уроке, в центре – многоугольник-прямоугольник.
2. Листок “К исследованию”.
3. Инструментарии учителя и учащихся (мел, указка, линейка, листок исследования, фигуры, ватман, маркер).

Метод урока:

• По взаимодействию учителя и учащихся – диалог-общение;
• По способу решения задач – частично-поисковый;
• По способу умственной деятельности — (СУД) развивающее обучение.

Форма урока — фронтальная, в парах, индивидуальная.

Тип урока — урок усвоения новых знаний, умений и навыков.

Структура урока — постепенное углубление в тему, гибкая, диалогическая.

Ход урока

Приветствие.

Урок прекрасен и приносит радость, когда мы мыслим, дружно работаем. Сегодня мы будем рассматривать фигуры, определять их названия, думать, искать и находить решения. Пожелаем друг другу успешной работы.

Актуализация знаний.

Рассмотрите фигуры (на доске многоугольники).

Они все вместе. Почему? Какой у них общий признак? (Многоугольники).

Назовите этот многоугольник (5-угольник, 6-угольник…)

Может быть, вы знаете, что такое площадь многоугольника?

Тогда покажите на одной из фигур.

(Обобщение учителем: площадь — часть плоскости внутри замкнутой геометрической фигуры.)

В русском языке это слово имеет несколько значений.

(Ученик по словарю знакомит со значениями.)

1. Часть плоскости внутри замкнутой геометрической фигуры.
2. Большое незастроенное и ровное место.
3. Помещение для какой-либо цели.

Какое из значений используется в математике?

В математике используется первое значение.

(На доске фигура).

Это многоугольник? Да.

Назовите фигуру по-другому. Прямоугольник.

Покажи длину, ширину.

Как найти площадь многоугольника?

Запишите при помощи букв и знаков формулу.

Если длина нашего прямоугольника 20 см, ширина 10см. Чему равна площадь?

Площадь равна 200 см 2

Подумайте, как приложить линейку, чтобы фигура разделилась на:

Увидели, из каких частей состоит фигура? А теперь, наоборот, по частям соберем целое.

(Части фигуры лежат на партах. Дети собирают из них прямоугольник).

Сделайте вывод по наблюдениям.

Целую фигуру можно разделить на части и из частей составить целую.

Дома на основе треугольников и четырехугольников составляли фигуры, силуэты. Вот какие они получились.

(Демонстрация рисунков, выполненных дома учащимися. Одна из работ анализируется).

Какие фигуры использовал? У тебя получился сложный многоугольник.

Постановка учебной задачи.

На уроке мы должны ответить на вопрос: как найти площадь сложного многоугольника?

Для чего человеку нужно находить площадь?

(Ответы детей и обобщение учителем).

Задача определения площади возникла из практики.

(Показывается план школьного участка).

Для того чтобы построить школу, сначала создали план. Потом разбивалась территория на участки определенной площади, размещались строения, клумбы, стадион. При этом участок имеет определенную форму — форму многоугольника.

Решение учебной задачи.

(Раздаются листы для исследования).

Перед вами фигура. Назовите ее.

Многоугольник, шестиугольник.

Найдем площадь многоугольника. Что для этого надо делать?

Разделить на прямоугольники.

(При затруднении будет другой вопрос: “Из каких фигур состоит многоугольник?”).

Из двух прямоугольников.

С помощью линейки и карандаша разделите фигуру на прямоугольники. Обозначьте цифрами 1 и 2 полученные части.

Проведем измерения.

Найдем площадь первой фигуры.

(Учащиеся предлагают следующие варианты решений и записывают их на доске).

• S 1 = 5 ? 2 = 10 см 2
• S 2 = 5 ? 1 = 5 см 2

Зная площадь частей, как найти площадь целой фигуры?

S = 10 + 5 = 15 см 2

• S 1 = 6 ? 2 = 12 см 2
• S 2 = 3 ? 1 = 3 см 2
• S = 12 + 3 = 15 см 2 .

Сравните результаты и сделайте вывод.

Проследим наши действия

Как находили площадь многоугольника?

Составляется и записывается на плакате алгоритм:?

1. Делим фигуру на части

2. Находим площади частей этих многоугольников (S 1 , S 2).

3. Находим площадь целого многоугольника (S 1 + S 2).

Проговорить алгоритм.

(Несколько учащихся проговаривают алгоритм).

Мы нашли два способа, а может, есть еще?

А можно фигуру достроить.

Сколько прямоугольников получилось?

Обозначим части 1 и 2. Проведем измерения.

Найдите площадь каждой части многоугольника.

• S 1= 6? 5=30см 2
• S 2 = 5 ? 3 = 15 см 2

Как найти площадь нашего шестиугольника?

S = 30 – 15 = 15 см 2

Составим алгоритм:

Достроили фигуру до прямоугольника

Нашли S 1 и S 2 .

Нашли разность S 1 – S 2 .

Сравните два алгоритма. Сделайте вывод. Какие действия одинаковые? Где разошлись наши действия?

Закройте глазки, опустите головки. Мысленно повторите алгоритм.

Мы провели исследовательскую работу, рассмотрели разные способы и теперь можем находить площадь любого многоугольника.

Проверка результативности.

Проверьте себя.

Перед вами многоугольники.

Найти площадь одной фигуры по выбору, при этом можете пользоваться разными способами.

Работа выполняется самостоятельно. Дети выбирают фигуру. Находят площадь одним из способов. Проверка – ключ на доске.

Что можно сказать о форме? (Форма разная)

А какова площадь этих многоугольников? (Площади этих многоугольников равны)

Оценивают результаты.

У кого правильно – поставь “+”.

У кого сомнения, затруднения – “?”

Консультанты оказывают помощь ребятам, ищут ошибки, помогают исправить.

Домашнее задание:

Составить свои листки исследования, вычислить площадь многоугольника разными способами.

Итог урока.

Итак, ребята, что вы расскажите родителям, о том как найти площадь геометрической фигуры – многоугольника.

Урок из серии «Геометрические алгоритмы »

Здравствуйте, дорогой читатель.

Решения многих задач вычислительной геометрии основывается на нахождении площади многоугольника . На этом уроке мы выведем формулу для вычисления площади многоугольника через координаты его вершин, напишем функцию для вычисления этой площади.

Задача. Вычислить площадь многоугольника , заданного координатами своих вершин, в порядке их обхода по часовой стрелке.

Сведения из вычислительной геометрии

Для вывода формулы площади многоугольника нам понадобятся сведения из вычислительной геометрии, а именно, понятие ориентированной площади треугольника.

Ориентированная площадь треугольника – это обычная площадь, снабженная знаком. Знак ориентированной площади треугольника АВС такой же, как у ориентированного угла между векторами и. То есть ее знак зависит от порядка перечисления вершин.

На рис. 1 треугольник АВС – прямоугольный. Его ориентированная площадь равна (она больше нуля, так как пара, ориентирована положительно). Эту же величину можно вычислить другим способом.

Пусть О – произвольная точка плоскости. На нашем рисунке площадь треугольника ABC получится, если из площади треугольника OBC вычесть площади OAB и OCA. Таким образом, нужно просто сложить ориентированные площади треугольников OAB, OBC и OCA. Это правило работает при любом выборе точки О .

Точно так же для вычисления площади любого многоугольника нужно сложить ориентированные площади треугольников

В сумме получится площадь многоугольника, взятая со знаком плюс, если при обходе ломаной многоугольника находится слева (обход границы против часовой стрелки), и со знаком минус, если он находится справа (обход по часовой стрелке).

Итак, вычисление площади многоугольника свелось к нахождению площади треугольника. Посмотрим, как выразить ее в координатах.

Векторное произведение двух векторов на плоскости есть площадь параллелограмма, построенного на этих векторах.2 \Rightarrow S_{\text{пр-к}}=ab \end{multline*}\)

Определение

Высота параллелограмма — это перпендикуляр, проведенный из вершины параллелограмма к стороне (или к продолжению стороны), не содержащей эту вершину.
Например, высота \(BK\) падает на сторону \(AD\) , а высота \(BH\) — на продолжение стороны \(CD\) :

Теорема: площадь параллелограмма

Площадь параллелограмма равна произведению высоты и стороны, к которой проведена эта высота.

Доказательство

Проведем перпендикуляры \(AB»\) и \(DC»\) , как показано на рисунке. Заметим,что эти перпендикуляры равны высоте параллелограмма \(ABCD\) .

Тогда \(AB»C»D\) – прямоугольник, следовательно, \(S_{AB»C»D}=AB»\cdot AD\) .

Заметим, что прямоугольные треугольники \(ABB»\) и \(DCC»\) равны. Таким образом,

\(S_{ABCD}=S_{ABC»D}+S_{DCC»}=S_{ABC»D}+S_{ABB»}=S_{AB»C»D}=AB»\cdot AD.\)

\[{\Large{\text{Площадь треугольника}}}\]

Определение

Будем называть сторону, к которой в треугольнике проведена высота, основанием треугольника.

Теорема

Площадь треугольника равна половине произведения его основания на высоту, проведенную к этому основанию.

Доказательство

Пусть \(S\) – площадь треугольника \(ABC\) . Примем сторону \(AB\) за основание треугольника и проведём высоту \(CH\) . Докажем, что \ Достроим треугольник \(ABC\) до параллелограмма \(ABDC\) так, как показано на рисунке:

Треугольники \(ABC\) и \(DCB\) равны по трем сторонам (\(BC\) – их общая сторона, \(AB = CD\) и \(AC = BD\) как противоположные стороны параллелограмма \(ABDC\)), поэтому их площади равны. Следовательно, площадь \(S\) треугольника \(ABC\) равна половине площади параллелограмма \(ABDC\) , то есть \(S = \dfrac{1}{2}AB\cdot CH\) .

Теорема

Если два треугольника \(\triangle ABC\) и \(\triangle A_1B_1C_1\) имеют равные высоты, то их площади относятся как основания, к которым эти высоты проведены.

Следствие

Медиана треугольника делит его на два треугольника, равных по площади.

Теорема

Если два треугольника \(\triangle ABC\) и \(\triangle A_2B_2C_2\) имеют по равному углу, то их площади относятся как произведения сторон, образующих этот угол.

Доказательство

Пусть \(\angle A=\angle A_2\) . Совместим эти углы так, как показано на рисунке (точка \(A\) совместилась с точкой \(A_2\)):

Проведем высоты \(BH\) и \(C_2K\) .

Треугольники \(AB_2C_2\) и \(ABC_2\) имеют одинаковую высоту \(C_2K\) , следовательно: \[\dfrac{S_{AB_2C_2}}{S_{ABC_2}}=\dfrac{AB_2}{AB}\]

Треугольники \(ABC_2\) и \(ABC\) имеют одинаковую высоту \(BH\) , следовательно: \[\dfrac{S_{ABC_2}}{S_{ABC}}=\dfrac{AC_2}{AC}\]

Перемножая последние два равенства, получим: \[\dfrac{S_{AB_2C_2}}{S_{ABC}}=\dfrac{AB_2\cdot AC_2}{AB\cdot AC} \qquad \text{ или } \qquad \dfrac{S_{A_2B_2C_2}}{S_{ABC}}=\dfrac{A_2B_2\cdot A_2C_2}{AB\cdot AC}\]

Теорема Пифагора

В прямоугольном треугольнике квадрат длины гипотенузы равен сумме квадратов длин катетов:

Верно и обратное: если в треугольнике квадрат длины одной стороны равен сумме квадратов длин других двух сторон, то такой треугольник прямоугольный.

Теорема

Площадь прямоугольного треугольника равна половине произведения катетов.

Теорема: формула Герона

Пусть \(p\) – полупериметр треугольника, \(a\) , \(b\) , \(c\) – длины его сторон, тогда его площадь равна \

\[{\Large{\text{Площадь ромба и трапеции}}}\]

Замечание

Т.к. ромб является параллелограммом, то для него верна та же формула, т.е. площадь ромба равна произведению высоты и стороны, к которой проведена эта высота.

Теорема

Площадь выпуклого четырехугольника, диагонали которого перпендикулярны, равна половине произведения диагоналей.

Доказательство

Рассмотрим четырехугольник \(ABCD\) . Обозначим \(AO=a, CO=b, BO=x, DO=y\) :

Заметим, что данный четырехугольник составлен из четырех прямоугольных треугольников , следовательно, его площадь равна сумме площадей этих треугольников:

\(\begin{multline*} S_{ABCD}=\frac12ax+\frac12xb+\frac12by+\frac12ay=\frac12(ax+xb+by+ay)=\\ \frac12((a+b)x+(a+b)y)=\frac12(a+b)(x+y)\end{multline*}\)

Следствие: площадь ромба

Площадь ромба равна половине произведения его диагоналей: \

Определение

Высота трапеции – это перпендикуляр, проведенный из вершины одного основания к другому основанию.

Теорема: площадь трапеции

Площадь трапеции равна произведению полусуммы оснований на высоту.

Доказательство

Рассмотрим трапецию \(ABCD\) с основаниями \(BC\) и \(AD\) . Проведем \(CD»\parallel AB\) , как показано на рисунке:

Тогда \(ABCD»\) – параллелограмм.

Проведем также \(BH»\perp AD, CH\perp AD\) (\(BH»=CH\) – высоты трапеции).

Тогда \(S_{ABCD»}=BH»\cdot AD»=BH»\cdot BC, \quad S_{CDD»}=\dfrac12CH\cdot D»D\)

Т.к. трапеция состоит из параллелограмма \(ABCD»\) и треугольника \(CDD»\) , то ее площадь равна сумме площадей параллелограмма и треугольника, то есть:

\ \[=\dfrac12 CH\left(BC+AD»+D»D\right)=\dfrac12 CH\left(BC+AD\right)\]

Каждый, кто изучал в школе математику и геометрию, хотя бы поверхностно знает эти науки. Но со временем, если в них не практиковаться, познания забываются. Многие даже считают, что только зря потратили своё время, изучая геометрические расчёты. Однако они ошибаются. Технические работники выполняют повседневную работу, связанную с геометрическими расчётами. Что касается расчета площади многоугольника, то и эти знания находят своё применение в жизни. Понадобятся они хотя бы для того, чтобы рассчитать площадь земельного участка . Итак, давайте узнаем, как найти площадь многоугольника.

Определение многоугольника

Сначала определимся с тем, что такое многоугольник. Это плоская геометрическая фигура, которая образовалась в результате пересечения трех или более прямых. Другое простое определение: многоугольник — это замкнутая ломаная. Естественно, при пересечении прямых образуются точки пересечения, их количество равно количеству прямых, образовывающих многоугольник. Точки пересечения называют вершинами, а отрезки, образованные от прямых, — сторонами многоугольника. Смежные отрезки многоугольника находятся не на одной прямой. Отрезки, являющиеся несмежными, — это те, которые не проходят через общие точки.

Сумма площадей треугольников

Как находить площадь многоугольника? Площадь многоугольника — это внутренняя часть плоскости, которая образовалась при пересечении отрезков или сторон многоугольника. Поскольку многоугольник — это сочетание таких фигур, как треугольник, ромб, квадрат, трапеция, то универсальной формулы для вычисления его площади просто нет. На практике наиболее универсальным является метод разбиения многоугольника на более простые фигуры, нахождение площади которых не вызывают затруднений. Сложив суммы площадей этих простых фигур , получают площадь многоугольника.

Через площадь окружности

В большинстве случаев многоугольник имеет правильную форму и образует фигуру с равными сторонами и углами между ними. Рассчитать площадь в этом случае очень просто при помощи вписанной или описанной окружности. Если известна площадь окружности, то её необходимо умножить на периметр многоугольника, а затем полученное произведение поделить на 2. В итоге получается формула расчёта площади такого многоугольника: S = ½∙P∙r., где P — площадь окружности, а r — периметр многоугольника.

Метод разбиения многоугольника на «удобные» фигуры — самый популярный в геометрии, он позволяет быстро и правильно найти площадь многоугольника. 4 класс средней школы обычно изучает такие методы.

Площадь, одна из основных величин, связанных с геометрическими фигурами . В простейших случаях измеряется числом заполняющих плоскую фигуру единичных квадратов, т. е. квадратов со стороной, равной единице длины. Вычисление П. было уже в древности… …

У этого термина существуют и другие значения, см. Площадь (значения). Площадь плоской фигуры аддитивная числовая характеристика фигуры, целиком принадлежащей одной плоскости. В простейшем случае, когда фигуру можно разбить на конечное… … Википедия

I Площадь одна из основных величин, связанных с геометрическими фигурами. В простейших случаях измеряется числом заполняющих плоскую фигуру единичных квадратов, т. е. квадратов со стороной, равной единице длины. Вычисление П.… … Большая советская энциклопедия

У этого термина существуют и другие значения, см. Площадь (значения). Площадь Размерность L² Единицы измерения СИ м² … Википедия

Ж. 1. Часть земной поверхности , пространство, естественно ограниченное или специально выделенное для какой либо цели. отт. Водное пространство. отт. Большое, ровное место, пространство. 2. Ровное незастроенное пространство общественного… … Современный толковый словарь русского языка Ефремовой

Эта статья предлагается к удалению. Пояснение причин и соответствующее обсуждение вы можете найти на странице Википедия:К удалению/2 сентября 2012. Пока процесс обсуждения не завершён, статью можно попытаться улучшить, однако следует… … Википедия

Две фигуры в R2, имеющие равные площади и соответственно два многоугольника M1 и М 2 такие, что их можно разрезать на многоугольники так, что части, составляющие М 1, соответственно конгруэнтны частям, составляющим М 2. Для, равновеликость… … Математическая энциклопедия

В=7, Г=8, В + Г/2 − 1= 10 Теорема Пика классический результат комбинаторной геометрии и геометрии чисел. Площадь многоугольника с целочисле … Википедия

У этого термина существуют и другие значения, см. Теорема Пика. В = 7, Г = 8, В + Г/2 − 1 = 10 Формула Пика (или теорема Пика) классический результат комбинаторной геометрии и геометрии чисел. Площадь … Википедия

Область (связное открытое множество) на границе выпуклого тела в евклидовом пространстве Е 3. Вся граница выпуклого тела наз. полной В. п. Если тело конечно, то полная В. п. наз. замкнутой. Если тело бесконечно, то полная В. п. наз. бесконечной.… … Математическая энциклопедия

Как найти периметр и площадь сложной фигуры «Math :: WonderHowTo

В этом видеоуроке автор показывает, как найти периметр и площадь сложной фигуры. Он показывает, что сложную фигуру можно разделить на стандартные геометрические фигуры. В текущем примере он делит сложную фигуру на прямоугольник и треугольник. Теперь он вычисляет периметр, складывая три стороны прямоугольника и две стороны треугольника. Точно так же он вычисляет отдельные площади прямоугольника и треугольника и, наконец, складывает их, чтобы найти площадь всей сложной фигуры.В этом видео показано, как найти периметр и площадь сложной фигуры.

(1) Часть 1 из 2 — Как найти периметр и площадь сложной фигуры, (2) Часть 2 из 2 — Как найти периметр и площадь сложной фигуры

Хотите освоить Microsoft Excel и взять свой перспективы работы на дому на новый уровень? Начните свою карьеру с помощью нашего пакета обучения Microsoft Excel Premium A-to-Z из нового магазина гаджетов и получите пожизненный доступ к более чем 40 часам инструкций от базового до расширенного по функциям, формулам, инструментам и многому другому.

Купить сейчас (97% скидка)>

Другие выгодные предложения, которые стоит проверить:

Как найти периметр из области — Видео и стенограмма урока

Периметр квадрата

Давайте начнем с квадрата и изучим этот пример задачи. Найдите периметр квадрата площадью 64 квадратных метра.

Шаг 1

Запомните формулы для площади и периметра квадрата. Площадь квадрата составляет a = s 2, или сторона, умноженная на сторону, в то время как периметр равен p = 4 s , или в 4 раза s .

Шаг 2

Найдите длину одной стороны, подставив значение площади в формулу и решив для s. В данном случае 64 = с 2, поэтому с = 8.

Шаг 3

Подставьте значение s (длина стороны) в формулу периметра и решите.

p = 4 x 8, поэтому p = 32

Периметр круга

Затем давайте рассмотрим пример задачи, чтобы найти периметр круга по его площади.Найдите периметр круга площадью 9 пикселей.

Шаг 1

Запомните формулы для площади и периметра круга. Площадь круга составляет a = pi * радиус 2, в то время как периметр круга, более известный как окружность , составляет p = 2pi * radius.

Шаг 2

Найдите длину радиуса, подставив площадь и решив формулу

9pi = pi * r 2

Разделите на пи, чтобы получить: 9 = r 2

r = 3

Шаг 3

Подставьте значение r в формулу периметра

p = 2 * pi * 3

p = 6pi

Периметр прямоугольника

Невозможно определить периметр прямоугольника, учитывая только площадь.Площадь прямоугольника зависит от двух неизвестных, длины и ширины, поэтому вам необходимо указать хотя бы одну сторону прямоугольника вместе с площадью, чтобы определить другую сторону и, таким образом, периметр.

Рассмотрим пример задачи. Найдите периметр прямоугольника длиной 4 и площадью 36м2.

Шаг 1

Запомните формулу для периметра и площади прямоугольника. Площадь прямоугольника составляет a = длина * ширина, а периметр равен p = (2 * длина) + (2 * ширина)

Шаг 2

Подставьте известные значения в формулу площади

36 = 4 * w

36/4 = w

w = 9

Шаг 3

Подставьте значения длины и ширины в формулу периметра.

p = 2 * 4 + 2 * 9

p = 8 + 18 = 26

Форматирование ответов

Ответы для каждого из этих вычислений будут в стандартных единицах , а не в квадрате. Вы должны использовать то же измерение, что и в исходной задаче, чтобы отформатировать свой ответ.

В примере задачи нахождения периметра квадрата площадь была указана в квадратных метрах, поэтому периметр должен быть указан в метрах. Таким образом, ответ — 32м.Если исходная задача не дает результатов, в ответе не следует использовать никакие измерения.

Как и в случае с квадратом, ответ для периметра круга должен быть дан в стандартных единицах исходной меры, если не была указана никакая мера. В этом примере измерения не проводились, поэтому ответ — 6 * пи. Обычно используется значение числа Пи 3,14159, поэтому также можно вычислить 6 * 3,14159, чтобы получить 18,84954 в качестве ответа на периметр этого круга.

Подобно другим примерам, с прямоугольником, если площадь дана в квадратах, периметр должен быть в стандартных единицах.Здесь правильно отформатированный ответ — 26м.

Советы для всех правильных форм

Помните, что правильных форм — это формы с равными сторонами. Чтобы найти периметр правильной формы из области этой формы, вам необходимо знать формулы для площади и периметра формы.

Шаг 1 — подставить площадь в формулу площади и найти длину одной стороны. Поскольку это правильная форма, вы знаете, что все стороны равны.

Шаг 2 — подставить значение стороны в формулу периметра и решить.

Шаг 3 просто обеспечивает правильное форматирование ответа. Периметр всегда указывается в стандартных единицах.

Результаты обучения

После завершения этого урока учащиеся должны уметь:

• Рассчитывать периметр квадрата, круга и прямоугольника с использованием площади
• Вспомните, как форматировать вычисления периметра

Калькулятор прямоугольников

. Найдите площадь и периметр любого прямоугольника

Если вам нужно знать площадь ковра, участка, экрана телевизора, прямоугольного бассейна или окна, этот прямоугольный калькулятор решит вашу проблему в мгновение ока! Все, что вам нужно сделать, это ввести длину и ширину (или диагональ) и позволить вычислению прямоугольника найти значения P (периметр) и A (площадь).Продолжайте читать, если вы хотите понять, что такое прямоугольник, вас интересуют определение прямоугольника, формулы, свойства прямоугольника … Или вы просто хотите узнать, как найти площадь прямоугольника.

Поскольку вы уже здесь, мы полагаем, что другие наши калькуляторы геометрических фигур могут быть вам интересны. Взгляните на наши замечательные инструменты, поиграйте с ними и опробуйте их!

Прямоугольник — это пример четырехугольной формы. Может быть, вы хотите посмотреть другие?

Что такое прямоугольник? Определение прямоугольника

Прямоугольник — это четырехугольник с четырьмя прямыми углами .Его также можно определить по-другому: параллелограмм, содержащий прямой угол — если один угол прямой, остальные должны быть такими же. Более того, каждая сторона прямоугольника имеет ту же длину, что и противоположная ему. Он также имеет неравные смежные стороны, в отличие от квадрата, который является частным случаем прямоугольника.

Если вы немного знаете латынь, название фигуры обычно многое объясняет. Слово прямоугольник происходит от латинского rectangulus . Это комбинация rectus (что означает «прямой, прямой») и angulus (угол), поэтому оно может служить простым базовым определением прямоугольника.

Как найти площадь прямоугольника?

На изображении выше показан типичный прямоугольник. У него четыре стороны и четыре прямых угла. Длины его сторон обозначены как a и b , а длина диагонали обозначена как d .

Если все стороны прямоугольника равны по длине, он называется квадратом .

Площадь прямоугольника — это пространство, ограниченное его сторонами, или, другими словами, в пределах периметра прямоугольника.Чтобы найти площадь прямоугольника, все, что вам нужно сделать, это умножить стороны прямоугольника a и b :

Площадь = a * b

Формулы прямоугольника

В нашем калькуляторе прямоугольников реализованы следующие формулы:

• Для площади прямоугольника : А = а * б

• Для периметра прямоугольника : Р = 2 * (а + б)

• Для диагонали прямоугольника : d² = a² + b²

Если вас интересует площадь трехмерных тел, а не двумерные формы, воспользуйтесь калькулятором площади поверхности.

Вычисление прямоугольника: найти A (площадь)

Поскольку мы знаем формулу площади прямоугольника A = a * b , давайте на примере покажем, как можно вычислить это свойство:

1. Выберите длину прямоугольника — например, a = 5 см .
2. Определитесь с шириной прямоугольника — например, b = 6 см .
3. Умножьте эти два значения: A = 5 см * 6 см = 30 см² .
4. Площадь прямоугольника 30 см².

Вычисление прямоугольника: найти P (периметр)

Давайте узнаем, как найти периметр прямоугольника. Как обычно, периметр представляет собой сумму всех сторон фигуры:

P = a + b + a + b

, которое можно записать как:

P = 2 * (a + b)

Возьмем для примера тот же прямоугольник:

1. Выбираем длину прямоугольника — a = 5 см в нашем случае .
2. Определитесь с шириной прямоугольника — e.грамм. b = 6 см .
3. Сложите эти два значения: a + b = 5 + 6 = 11 см .
4. Умножьте результат на 2: P = 2 * 11 = 22 см .
5. Поехали! Периметр нашего прямоугольника 22 см.

Вычисление прямоугольника: найти D (диагональ)

Диагональ прямоугольника — это отрезок, соединяющий две противоположные вершины прямоугольника. Рассчитаем длину диагонали примерного прямоугольника:

1. Выберите длину прямоугольника — например, a = 5 см .
2. Определитесь с шириной прямоугольника — например, b = 6 см .
3. Вычислите a в степени двойки: a² = 25 см² .
4. Вычислите b в степени двойки: b² = 36 см² .
5. Сложите эти два значения: a² + b² = 25 + 36 = 61 см² .
6. Наконец, извлеките квадратный корень из результата: d = √ (a² + b²) = √61 ~ 7,81 см .
7. Длина по диагонали 7,81 см.

Естественно, вместо того, чтобы вычислять все эти значения вручную, вы можете использовать эту область прямоугольного калькулятора. Вы также можете использовать его в обратном порядке — например, чтобы вычислить ширину прямоугольника с известной длиной и периметром.

Золотой прямоугольник

Особый тип прямоугольника, называемый золотым прямоугольником, показан на изображении выше. Такой прямоугольник удовлетворяет следующему условию:

(a + b) / a = a / b = ϕ

, где φ — золотое сечение, равное 1.618.

Как вы, наверное, помните, отношение — это отношение между двумя величинами, часто представляемое в виде дроби.

Знаете ли вы, что золотой треугольник можно построить, используя только линейку и циркуль ? Всего несколько шагов!

1. Нарисуйте квадрат.
2. Проведите линию от середины одной стороны квадрата до противоположного угла.
3. Нарисуйте круг с радиусом, равным этой линии, с центром в средней точке, как на картинке.
4. Точка, где круг встречается со стороной расширенного квадрата, является следующим углом золотого прямоугольника.
5. Найдите последнюю вершину и завершите золотой прямоугольник.

Даааааааааааааааааааааааааааааааааа! Это было не так уж сложно, правда?

Свойства прямоугольника

Прямоугольники обладают множеством интересных свойств. Прямоугольник:

• — это циклический — это означает, что все углы лежат на одной окружности.
• — это равноугольный — все его углы равны 90 градусам.
• — это прямолинейный, — его стороны пересекаются под прямым углом.
• имеет две линии отражательной симметрии — вертикальную и горизонтальную через центр.
• имеет две диагонали, которые пересекают друг друга . Вы можете найти длину диагонали, используя теорему Пифагора.
• противоположные стороны прямоугольника параллельны друг другу и имеют одинаковую длину.

Другие менее известные объекты прямоугольной формы:

• Пересечение диагоналей — это центр описанной окружности. — существует круг, центр которого находится в этой точке, и он проходит через четыре угла.
• В прямоугольнике с разной длиной стороны (попросту говоря — не квадрате) невозможно нарисовать вписанную окружность.
• Линии, соединяющие середины сторон прямоугольника, образуют ромб, который составляет половину площади прямоугольника. Стороны фигуры параллельны диагоналям.

Вы можете думать и о своей собственности; например по поводу вращения прямоугольника — по бокам или диагонали, чтобы получился цилиндр или конус соответственно.

Прямоугольник по сравнению с другими формами. Квадрат — это прямоугольник?

TL; DR:

1. Является ли квадрат прямоугольником? ДА .
2. Прямоугольник — это параллелограмм? ДА .
3. Прямоугольник — это ромб? В общем — НЕТ. Только если это квадрат (все углы ромба равны 90 градусам).
4. Ромб — это прямоугольник? В общем — НЕТ. Только если это квадрат (все стороны прямоугольника одинаковой длины).
5. Прямоугольник — это четырехугольник? ДА конечно.
6. Прямоугольник — это трапеция? ДА .

Хотите знать, является ли квадрат прямоугольником или прямоугольником параллелограммом? Взгляните на картинку, и у вас больше не должно возникнуть сомнений относительно соотношения четырехугольников:

Как читать эту диаграмму? Начнем с нашего прямоугольника. Непосредственно к форме соединены три фигуры: квадрат, параллелограмм и равнобедренная трапеция.Итак, если фигура находится над интересующей нас фигурой — например, квадрат или прямоугольник — мы можем сказать, что:

• Каждый квадрат — это прямоугольник , а квадрат — это частный случай прямоугольника .

Для двух других цифр мы можем сформулировать аналогично:

• Каждый прямоугольник — это параллелограмм , а прямоугольник — это частный случай параллелограмма .
• Каждый прямоугольник — это трапеция , а прямоугольник — это частный случай трапеции .

Странный забавный факт: какая страна самой прямоугольной формы в мире?

Существует множество различных рейтингов, оценивающих страны — по их регионам, населению, уровню образования или лауреатам Нобелевской премии. Но задумывались ли вы когда-нибудь, , кто является победителем конкурса самых прямоугольных стран? Австралийский геостатист Дэвид Барри рассчитал параметр прямоугольности для всех стран мира и составил рейтинг. Он выяснил, что самая прямоугольная страна — это Египет, а титул «наименее прямоугольной страны в мире» достается Мальдивам (однако автор признает, что расчеты для стран, состоящих из множества небольших островов, могут быть ужасно ошибочными).Взгляните на таблицу ниже и выберите первые десять стран, а также страны с наименее прямоугольной формой.

Наивысшие баллы в рейтинге прямоугольности. Индекс 1 — идеальный прямоугольник, 0 — бесконечное количество бесконечно малых островов. Таблица адаптирована с веб-страницы мистера Барри, как изображение мира ниже.

Египет — лидер, но это никого не должно удивлять, проверяя очертания этой страны на карте. США находятся в середине рейтинга, в основном из-за неординарности Аляски и Гавайев.Заблуждение заключается в том, что вторая по величине прямоугольность страны — Ватикан — одновременно является четвертой по округлости страной, а Польша, занимающая 5-е место в классификации округлости, занимает 9-е место в рейтинге прямоугольности.

Как это вообще возможно быть прямоугольным и круглым одновременно ?! Как вы можете догадаться, все дело в определении прямоугольности и округлости, которые могут не подходить для сложных или рассеянных форм — и обычно такими примерами являются границы стран, содержащие острые края, небольшие острова или колонии где-то в другой части. Глобус.Если вас интересует эта тема, вы можете взглянуть на это объяснение и обсуждение результатов. Также в круглом калькуляторе вы найдете специальный абзац о округлости стран с аналогичной таблицей и примерами.

Можно было подумать, что мир было бы легче нарисовать, если бы каждая страна была прямоугольной … Или нет?

Прямоугольник

Форма прямоугольника используется во многих периодических моделях тесселяции. Его можно использовать для облицовки стен из кирпича, плитки для пола, тротуара или различной мозаики.Ниже вы найдете несколько популярных паттернов:

• Стыковка в стопу — это наиболее распространенный и простой способ укладки плитки, так как плитки укладываются по прямым линиям.

• Спусковое соединение — типично для мостовых и кирпичных связей.

• Елочка — деревянные полы хорошо смотрятся с таким рисунком.

• Basketweave — часто используется для коридоров или уличных дорожек.

Конечно, плитка бывает всех форм и размеров — довольно популярны шестиугольники и восьмиугольники с квадратами. Форма пятиугольника должна быть неправильной, чтобы образовался мозаичный узор.

Прямоугольники в повседневной жизни: прямоугольная форма тела, прямоугольный бассейн, прямоугольная скатерть …

Одной из самых популярных проблем, связанных с прямоугольниками, является тип тела. Если вам интересно, на какую форму ваша фигура больше всего похожа, воспользуйтесь нашим калькулятором формы тела.Все, что вам нужно сделать, это измерить свой бюст, талию, бедра и высокие бедра и ввести значения в инструмент. Тогда вы получите информацию о вашей фигуре. Например, прямоугольная фигура определяется как «мальчишеский» тип телосложения — ваши бедра, талия и грудь примерно одинакового размера. Ваше тело стройно и спортивно. Ознакомьтесь также с нашим калькулятором жировых отложений, который поможет вам оценить процентное содержание жировых отложений в общей массе вашего тела.

Удивительно, но нас окружают прямоугольные предметы.Поэтому наш калькулятор прямоугольников может быть полезен не только на уроках математики, но и в решении повседневных задач. Конечно, в реальности вы не найдете идеального прямоугольника, поскольку он всегда имеет третье измерение; но если он мал по сравнению с двумя другими измерениями, приближение достаточно хорошее.

• Прямоугольные скатерти — учитывая размер вашего стола, вы можете узнать, какая скатерть вам понадобится, а также сколько кружевной ленты или ленты для подшивки нужно использовать.
• Двери или оконное стекло — ваше оконное стекло разбило шторм или мяч для гольфа? Подсчитайте площадь и оцените стоимость ремонта, учитывая цену за квадратный метр или квадратный метр.
• Экраны электронных устройств — планшетов, смартфонов, телевизоров — используйте эту область прямоугольного калькулятора или наш специальный инструмент размера экрана, чтобы оценить, сколько места на стене займет ваш экран — или насколько большой экран вашего телефона хочу купить есть. Если вас интересует плотность пикселей, попробуйте наш калькулятор PPI
• Классные доски, зеркала, рамки, холст, листы бумаги, записные книжки, конверты, деньги, флаги, прямоугольные бассейны … Это бесконечный список!

Посмотрите, можете ли вы найти больше прямоугольных предметов вокруг себя? Что вы можете!

Площадь и периметр на координатной плоскости

Возможно, вы знакомы с определением площади и периметра двумерных фигур.Однако это может показаться немного другой задачей, когда она представлена ​​на координатной плоскости.

Example # 1

Определите периметр и площадь прямоугольника ниже.

Обратите внимание, что длины не указаны. Вместо этого вы должны использовать график для определения информации.

Счетчик поможет вам определить длину сторон.

Теперь, когда у вас есть длины всех сторон, вы можете сложить их, чтобы получить периметр.

P = 10 + 10 + 11 + 11

P = 42 единицы

Вы также можете использовать длину для вычисления площади прямоугольника.

Для прямоугольника площадь равна длине, умноженной на ширину.

A = lw

A = (10 единиц) (11 единиц)

A = 110 единиц ²

Другой вариант, хотя и довольно утомительный, — это подсчет всех квадратов внутри прямоугольника. Если бы вы сделали это, вы бы заметили, что есть 110 квадратов. Таким образом, площадь составляет 110 кв.

Пример № 2

В этом случае при определении длины каждой стороны обязательно подсчитывайте длины, а не фактические квадраты.

Несмотря на то, что 12 целых квадратов не помещаются в основании треугольника, существует 12 отрезков.

По графику невозможно определить длину самой длинной стороны. Это один из недостатков предоставления информации в координатной плоскости. Теорема Пифагора может использоваться для вычисления третьей стороны.(Помните, что самая длинная сторона должна быть помечена как c в формуле a ² + b ² = c ² .)

a ² + b ² = c ²

12 ² + 10 ² = c ²

144 + 100 = c ²

244 = c ²

√244 = c

15,6 ≈ c

Это примерная длина третьей стороны треугольника.

Теперь мы можем определить примерный периметр треугольника.

P = 10 + 12 + 15,6

P = 37,6 единиц

Для площади мы можем использовать формулу A = ½ bh. Обязательно используйте основание
и высоту, которые совпадают под прямым углом.

A = ½ bh

A = ½ (12 шт.) (10 шт.)

A = 60 шт. ²

Пример № 3 Определите периметр и площадь неправильной фигуры.

Начнем с периметра. Сначала определите длину всех частей.

Затем сложите длины вместе, чтобы получить периметр.

P = 8 + 4 + 3 + 13 + 3 + 2 + 2 + 3 + 6 + 16

P = 60 единиц

Для области начните с разделения фигуры на прямоугольники. Эту форму можно разделить по-разному. Вот одна возможность.

Прямоугольник # 1

A = lw

A = (13 единиц) (3 единицы)

A = 39 единиц ²

Прямоугольник # 2

A = lw

A = ( 3 единицы) (2 единицы)

A = 6 единиц ²

Прямоугольник # 3

A = lw

A = (16 единиц) (8 единиц)

A = 128 единиц ²

Затем добавьте площади всех частей, чтобы получить общую площадь формы.

Общая площадь = 39 + 6 + 128

Общая площадь = 173 единицы ²

Давайте рассмотрим

Когда двумерные фигуры показаны на координатной плоскости, это сочетание подсчета и теоремы Пифагора можно использовать для определения длины каждой стороны. Затем сложите длины, чтобы определить периметр, или используйте основные формулы площади для треугольников и прямоугольников, чтобы определить площадь фигуры.

Площадь составных фигур — Периметр и площадь — WJEC — GCSE Maths Numeracy (WJEC) Revision

Чтобы вычислить площадь составной фигуры, вы должны разделить фигуру на прямоугольники, треугольники или другие фигуры, вы можете найти площадь, а затем снова сложите области вместе.

Возможно, вам придется рассчитать недостающую длину, прежде чем определять площадь некоторых фигур.

Площадь сложной формы

Вычислите площадь этой сложной формы.

Область сложной формы

Разделите фигуру на прямоугольники и треугольники и пометьте каждый из них.

Площадь сложной формы

Прямоугольник A: сначала вычислите длину прямоугольника. Общая длина фигуры 12 см, вычесть 4 см и 1 см = 7 см.

Площадь сложной формы

Площадь прямоугольника A = длина × ширина = 10 × 7 = 70 см в квадрате.

Площадь сложной формы

Прямоугольник B: сначала вычислите длину прямоугольника. Длина прямоугольника B = 4 см + 1 см = 5 см.

Площадь сложной формы

Площадь прямоугольника B = длина × ширина = 5 × 4 = 20 см в квадрате

Площадь сложной формы

Треугольник C: сначала вычислите высоту треугольника. Общая высота фигурки 10 см. Если вычесть 4 см длины квадрата, на котором находится треугольник, получаем 6 см для высоты треугольника.

Площадь сложной формы

Площадь треугольника C = ½ × основание × высота = ½ × 1 × 6 = квадрат 3 см.

Площадь сложной формы

Сложите площади всех фигур. Общая площадь = A + B + C = 70 + 20 + 3 = 93 см в квадрате.

Другие составные формы могут иметь вырезанные части. Чтобы определить площадь этих фигур, вы должны вычислить площадь основной формы и вычесть площадь выреза.

Вопрос

Вычислите площадь закрашенной фигуры.

Показать ответ

1. Площадь прямоугольника = 15 × 20 = 300 мм ²
2. Площадь трапеции = ½ × (10 + 13) × 6 = ½ × 23 × 6 = ½ × 138 = 69 мм ²
3. Площадь закрашенной формы = 300 — 69 = 231 мм ²

Периметр и площадь | Математика для гуманитарных наук

Периметр

Периметр — это одномерное измерение, которое проводится вокруг внешней части замкнутой геометрической формы.Давайте начнем обсуждение концепции периметра с примера.

Управляемый пример

Рисунок 1.

Рисунок 2.

У Джозефа нет машины, поэтому он должен ездить на автобусе или идти пешком. По понедельникам он должен ехать в школу, на работу и снова домой. Его маршрут изображен на рисунке 1.

В этой ситуации очевидный вопрос: «сколько миль проезжает Джозеф по понедельникам»? Для вычисления мы каждое расстояние: 3 + 6 + 6 = 15.

Джозеф проезжает 15 миль по понедельникам.

Другой способ справиться с этой ситуацией — нарисовать фигуру, представляющую маршрут путешествия Джозефа и помеченную расстоянием от одного места до другого.

Обратите внимание, что маршрут Джозефа представляет собой замкнутую геометрическую фигуру с тремя сторонами (треугольник) (см. Рисунок 2). Что мы можем спросить об этой форме: «каков периметр треугольника»?

Периметр означает «расстояние вокруг замкнутой фигуры или фигуры», и для вычисления мы складываем каждую длину: 3 + 6 + 6 = 15

Наш вывод тот же, что и выше: Джозеф проезжает 15 миль по понедельникам.

Однако мы смоделировали ситуацию с помощью геометрической формы, а затем применили конкретную геометрическую концепцию ( периметр ) для вычисления расстояния, которое прошел Джозеф.

Записки по периметру

• Периметр — это одномерное измерение, которое представляет собой расстояние вокруг замкнутой геометрической фигуры или фигуры (без промежутков).
• Чтобы найти периметр, сложите длины каждой стороны формы.
• Если есть единицы, включите единицы в окончательный результат.Единицы измерения всегда будут одномерными (например, футы, дюймы, ярды, сантиметры и т. Д.).

Чтобы вычислить периметр, наши фигуры должны быть замкнуты. На рисунке 3 показана разница между закрытой фигурой и открытой фигурой.

Рисунок 3.

Пример 1

Найдите периметр для каждой из фигур ниже.

1. Сложите длины каждой стороны.
   
2. Иногда приходится делать предположения, если длина не указана.
   

Решения

1. 12 шт.
2. 40 футов

Пример 2

Как найти периметр этой более сложной формы?

Решение

Просто продолжайте добавлять длины сторон.6 + 7 + 4 + 4 + 5 + 6 + 2 = 34 шт.

Если вы внимательно посмотрите на формы в предыдущих примерах, вы можете заметить некоторые способы записать каждый периметр в виде более явной формулы. Посмотрите, соответствуют ли результаты того, что мы сделали, приведенным ниже формулам.

Форма		Периметр
Треугольник со сторонами, a , b , c :		[латекс] P = a + b + c \\ [/ латекс]
Квадрат с длиной стороны a :		[латекс] P = a + a + a + a \\ [/ latex] [латекс] P = 4a \\ [/ latex]
Прямоугольник со сторонами a , b :		[латекс] P = a + b + a + b \\ [/ латекс] [латекс] P = a + a + b + b \\ [/ латекс] [латекс] P = 2a + 2b \\ [ / латекс]

Окружность

Как вы понимаете, мы еще не обсуждали расстояние вокруг очень важной геометрической формы: круга! Расстояние по окружности имеет специальное название — окружность .Чтобы найти длину окружности, воспользуемся этой формулой: C = 2πr

Рисунок 4.

В этой формуле π произносится как «пи» и определяется как длина окружности круга, деленная на его диаметр: [latex] \ displaystyle \ pi = \ frac {C} {d} \\ [/ latex]. Обычно мы заменяем π приближением 3.14. Буква r представляет радиус круга.

Давайте посмотрим, откуда взялась формула для определения окружности. На рис. 4 показан общий круг с радиусом r.

Примечания о

C = 2π r

Помните, что в формуле при вычислении длины окружности C = 2π r , мы умножаем , обычно , заменяя 3,14 вместо π:

C = 2 × 3,14 × r

Часто использование () помогает облегчить просмотр различных частей формулы:

С = (2) × (3,14) × ( r )

Происхождение

C = 2π r

Как упоминалось ранее, специальное число π определяется как отношение длины окружности к ее диаметру.Мы можем записать это в форме уравнения как: [latex] \ displaystyle \ frac {C} {d} = \ pi \\ [/ latex]

Из нашей предыдущей работы мы знаем, что для определения неизвестного, C , мы можем переместить d на другую сторону уравнения, написав C = π d. Диаметр полностью пересекает середину круга, поэтому диаметр в два раза больше радиуса. Мы можем обновить C с точки зрения радиуса как C = π (2 r ). После небольшого изменения порядка, в котором написаны наши детали, мы можем сказать, что C = 2π r.

Давайте воспользуемся формулой, чтобы найти длину окружности нескольких окружностей.

Пример 3

Найдите длину окружности каждого из следующих кругов. Оставляйте свои ответы сначала в точном виде, а затем в округленном (до сотых разрядов). (Обратите внимание, что когда указан радиус, его значение центрируется над сегментом радиуса. Когда указан диаметр, его значение центрируется над сегментом диаметра.)

Решения

1. Точное значение 8π дюймов; округлено от точного ответа 25.13 дюймов; округлено с использованием 3,14 для π 25,12 из
2. Точное 12,44π м; округлено от точного ответа 39,08 м; округлено с использованием 3,14 для π 39,06 м

Точная форма и закругленная форма

• π — число в точной форме. Он не округлый.
• 3,14 — это приближение округленной формы для π

Почему важно, какую форму мы используем? Это важно, потому что при округлении мы вносим ошибку в окончательный результат. Для этого класса такая ошибка обычно приемлема. Однако вы обнаружите, что в других предметах, таких как физика или химия, такой уровень точности имеет большое значение.Давайте посмотрим на примере разницы в формах.

Пример 4

Радиус Луны составляет около 1079 миль. Что такое окружность? Давайте решим это, используя как точную, так и округленную форму:

Точное решение

[латекс] C = 2 \ pi {r} = 2 \ pi (1079) = 2158 \ pi \\ [/ latex]

Чтобы округлить от до точного решения, используйте кнопку π на калькуляторе, чтобы получить

[латекс] 2158 \ pi \ ок. 6779,56 \ [/ латекс]

Округленное решение

[латекс] C = 2 \ pi {r} = 2 (3.14) (1079) \ приблизительно 6776.12 \ [/ латекс]

Обратите внимание, что наши окончательные результаты отличаются. Эта разница — ошибка, созданная при использовании 3,14 в качестве начального приближения для π. Выполняя домашнее задание и тесты, внимательно читайте инструкции по каждой задаче, чтобы понять, какую форму использовать.

Пример 5

Найдите длину окружности или периметра для каждой описанной ниже ситуации. Включите рисунок формы с включенной информацией. Используйте примеры, чтобы определить, какие фигуры рисовать.Показать все работы. Как и в примерах, если включены единицы, то единицы должны присутствовать в вашем окончательном результате. Округлите до десятых, если не указано иное.

1. Найдите периметр квадрата со стороной 2,17 фута.
2. Найдите периметр прямоугольника со сторонами длиной 4,2 и 3,8.
3. Найдите периметр треугольника со сторонами длиной 2, 5, 7.
4. Найдите длину окружности радиуса 6 дюймов. Представьте ответ в точной форме, а также вычислите, используя 3.14 для π. Представьте округлую форму с точностью до десятых.
5. Найдите длину окружности круга диаметром 14,8 дюйма. Представьте ответ в точной форме, а также вычислите, используя 3,14 для π. Представьте округлую форму с точностью до десятых.

Решения

1. 8,68 футов
2. 16
3. 14
4. Точное 12π дюйма, округленное 37,7 дюйма
5. Точное значение 14,8π дюйма, округленное 46,5 дюйма

Пример 6

Определение расстояния вокруг нестандартных форм

Основные формулы для периметра прямых фигур и окружности круга помогут нам найти расстояние вокруг более сложных фигур.Найдите расстояние вокруг следующей формы. Округлите окончательный ответ до десятых и используйте 3,14 вместо π.

Решение

34,7 дюйм

Пример 7

Аппликации периметра и окружности

Наши знания основных геометрических фигур могут быть применены для решения «реальных» задач.

Уолли хочет добавить забор позади своего дома, чтобы дети могли безопасно играть (см. Диаграмму ниже). Он начал измерять свой двор, но отвлекся и забыл закончить измерения перед тем, как пойти в магазин.Если он помнит, что длина задней стены его дома составляет 15 ярдов, есть ли у него достаточно информации, чтобы купить необходимое ему ограждение? Если да, то сколько футов ему следует купить?

Решение

81 фут

Площадь

Давайте еще раз посмотрим на задний двор Уолли из примера 7, чтобы представить следующую концепцию: площадь.

Управляемый пример

Уолли успешно огородил свой двор, но теперь хочет добавить немного ландшафта и создать лужайку, как показано ниже.

Он направляется в местный магазин по продаже газонов и обнаруживает, что для того, чтобы определить, сколько дерна ему нужно, он должен вычислить площадь в квадратных футах той области, на которой он хочет добавить траву. По пути домой он понимает, что если разделит травянистую территорию на участки размером 1 фут на 1 фут, а затем пересчитает их, он сможет определить площадь в квадратных футах. Вот информация, которую Уолли собрал, когда вернулся домой.

Уолли правильно определил, что площадь прямоугольного травянистого участка составляет 30 квадратных футов.

Заметки о зоне

• Область — это двумерное измерение, которое представляет количество пространства внутри двухмерной фигуры.
• Чтобы найти площадь, посчитайте количество единичных квадратов внутри фигуры.
• Если есть единицы, включите единицы в окончательный результат. Единицы измерения всегда будут двухмерными (например, квадратные футы, квадратные ярды, квадратные мили и т. Д.)

Пример 8

Найдите область для каждой из фигур ниже.

1. Не забудьте посчитать единичные квадраты внутри фигуры.
   
2. Есть ли здесь шаблон, который облегчил бы нашу работу?
   

Пример 9

Как найти область для более сложных фигур? Разбейте области на формы, которые мы узнаем, и сложите значения областей вместе.

Если вы внимательно посмотрите на формы в предыдущих примерах, вы можете заметить некоторые способы записать каждую область в виде более явной формулы.2 \ [/ латекс] Прямоугольник со сторонами a , b

[латекс] A = a \ cdot {b} \\ [/ latex]

(Вы также увидите это как [latex] A = \ text {length} \ cdot \ text {width} \\ [/ latex])

Формулы площади для фигур ниже сложнее получить, поэтому формулы перечислены в таблице.

Форма	Форма
Треугольник высотой h и основанием b [латекс] \ displaystyle {A} = \ frac {1} {2} bh = \ frac {bh} {2} \\ [/ latex] Читается как «половина основания, умноженная на высоту» Обратите внимание, что h — это расстояние по прямой от вершины треугольника до другой стороны.2 \ [/ латекс] Читается как «пи, умноженный на радиус в квадрате»
	Если ваш треугольник такой, как показано на рисунке слева, то высота нарисована и измерена за пределами треугольника. Формула площади такая же.

Пример 10

Найдите область для каждой описанной ситуации. Создайте рисунок формы с включенной информацией. Показать все работы. Как и в примерах, если включены единицы, то единицы должны присутствовать в вашем окончательном результате.Используйте 3,14 для π и округляйте ответы до десятых, если необходимо.

1. Найдите площадь прямоугольника, длина которого составляет 12,9 метра, а высота составляет одну треть этой величины.
2. Найдите площадь треугольника с основанием [latex] \ displaystyle {24} \ frac {1} {2} \\ [/ latex] дюймов и высотой 7 дюймов.
3. Найдите площадь круга с радиусом [latex] \ displaystyle {2} \ frac {1} {3} \\ [/ latex] дюймов. Представьте ответ в точной форме, а также вычислите округленную форму, используя 3,14 для π. Представьте округлую форму с точностью до десятых.

Решения

1. 55,5 м ² или 55,5 кв.м (округлено)
2. 85,8 дюйма ² или 85,8 квадратных дюйма (округлено)
3. Точное 49/9 π дюйма ² , Округленное 17,1 дюйма ²

Пример 11

Найдите область в каждой описанной ситуации. Включите рисунок формы с включенной информацией. Показать все работы. Как и в примерах, если включены единицы, то единицы должны присутствовать в вашем окончательном результате.Округляйте ответы до десятых, если не указано иное.

1. Найдите площадь квадрата со стороной 4,2 фута.
2. Найдите площадь прямоугольника со сторонами длиной 4,2 и 3,8.
3. Найдите площадь треугольника высотой 7 дюймов и основанием 12 дюймов.
4. Найдите площадь круга радиусом 6 дюймов. Представьте ответ в точной форме, а также вычислите, используя 3,14 для π. Представьте округлую форму с точностью до десятых.

Решения

1. 17.64 фута ² или 17,64 квадратных футов
2. 16,0
3. 42 дюйма ² или 42 квадратных дюйма
4. Точное 36π в ² или 36π квадратных дюймов, округлено с использованием 3,14 для π 113,0 в ² или 113,0 квадратных дюймов

Пример 12

Нахождение области нестандартных форм

Основные формулы площади помогут нам найти площадь более сложных фигур. Это та же проблема, для которой мы нашли периметр ранее. Найдите площадь данной формы.Вычислить, используя 3,14 для π и округлить до ближайшей десятой.

Решение

Округлено с использованием 3,14 для π 25,9 дюйма ²

Пример 13

Применение площади и периметра

Мы можем объединить наши знания о площади / периметре для решения таких проблем, как эта.

Уолли все еще ремонтирует свой дом, и ему нужно завершить проект полов. Он хочет купить достаточно бамбукового пола, чтобы покрыть пространство в комнатах A, C и коридоре B, а также достаточно бамбуковой кромки для плинтусов во всех помещениях.Сколько квадратных футов пола и сколько футов плинтусов ему следует купить?

Решение

256 футов ² настил, 108 футов окантовка

Как найти площадь прямоугольника

Если вы считаете, что контент, доступный через Веб-сайт (как определено в наших Условиях обслуживания), нарушает одно или несколько ваших авторских прав, сообщите нам об этом, отправив письменное уведомление («Уведомление о нарушении»), содержащее в информацию, описанную ниже, назначенному ниже агенту.Если репетиторы университета предпримут действия в ответ на ан Уведомление о нарушении, он предпримет добросовестную попытку связаться со стороной, которая предоставила такой контент средствами самого последнего адреса электронной почты, если таковой имеется, предоставленного такой стороной Varsity Tutors.

Ваше Уведомление о нарушении прав может быть отправлено стороне, предоставившей доступ к контенту, или третьим лицам, таким как в виде ChillingEffects.org.

Обратите внимание, что вы будете нести ответственность за ущерб (включая расходы и гонорары адвокатам), если вы существенно искажать информацию о том, что продукт или действие нарушает ваши авторские права.Таким образом, если вы не уверены, что контент находится на Веб-сайте или по ссылке с него нарушает ваши авторские права, вам следует сначала обратиться к юристу.

Чтобы отправить уведомление, выполните следующие действия:

Вы должны включить следующее:

Физическая или электронная подпись правообладателя или лица, уполномоченного действовать от их имени; Идентификация авторских прав, которые, как утверждается, были нарушены; Описание характера и точного местонахождения контента, который, по вашему мнению, нарушает ваши авторские права, в \ достаточно подробностей, чтобы позволить репетиторам университетских школ найти и точно идентифицировать этот контент; например, мы требуем а ссылка на конкретный вопрос (а не только на название вопроса), который содержит содержание и описание к какой конкретной части вопроса — изображению, ссылке, тексту и т. д. — относится ваша жалоба; Ваше имя, адрес, номер телефона и адрес электронной почты; а также Ваше заявление: (а) вы добросовестно считаете, что использование контента, который, по вашему мнению, нарушает ваши авторские права не разрешены законом, владельцем авторских прав или его агентом; (б) что все информация, содержащаяся в вашем Уведомлении о нарушении, является точной, и (c) под страхом наказания за лжесвидетельство, что вы либо владелец авторских прав, либо лицо, уполномоченное действовать от их имени.

Отправьте жалобу нашему уполномоченному агенту по адресу:

Чарльз Кон Varsity Tutors LLC
101 S. Hanley Rd, Suite 300
St. Louis, MO 63105

Или заполните форму ниже:

.