Как определить объем цилиндра в воде – Калькулятор для расчета объема цилиндра

Как посчитать объем цилиндра — онлайн калькулятор

Чтобы посчитать объем цилиндра воспользуйтесь нашим удобным онлайн калькулятором:

Онлайн калькулятор

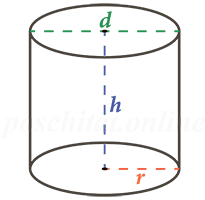
Найти чему равен объем цилиндра (V) можно зная (либо-либо):

• радиус r и высоту h цилиндра
• диаметр d и высоту h цилиндра
• площадь основания S_o и высоту h цилиндра
• площадь боковой поверхности S_b и высоту h цилиндра

Подставьте значения в соответствующие поля и получите результат.

Зная радиус r и высоту h

Чему равен объем цилиндра V если известны его радиус r и высота h?

Формула

V = π⋅r²⋅h

Пример

Если цилиндр имеет высоту h = 8 см, а его радиус r = 2 см, то:

V = 3.14156 ⋅ 2² ⋅ 8 = 3.14156 ⋅ 32 = 100.53 см³

Зная диаметр d и высоту h

Чему равен объем цилиндра

V если известны его диаметр d и высота h?

Формула

V = π⋅(^d/₂)²⋅h

Пример

Если цилиндр имеет высоту h = 5 см, а его диаметр d = 1 см, то:

V = 3.14156 ⋅ (¹/₂)² ⋅ 5 = 3.14156 ⋅ 1.25 ≈ 3.927 см³

Зная площадь основания S_o и высоту h

Чему равен объем цилиндра V если известны его площадь основания S_o и высота h?

Формула

V = S_o⋅h

Пример

Если цилиндр имеет высоту h = 10 см, а площадь его основания S_o = 5 см², то:

V = 10 ⋅ 5 = 50 см³

Зная площадь боковой поверхности S_b и высоту h

Чему равен объем цилиндра V если известны его площадь боковой поверхности

S_b и высота h?

Формула

V = ^S_b2/_4πh

Пример

Если цилиндр имеет высоту h = 5 см, а площадь его боковой поверхности S_b = 30 см², то:

V = ³⁰²/ _{4 ⋅ 3.14⋅ 5} = ⁹⁰⁰/_62.8 = 14.33 см³

poschitat.online

Объем цилиндра ℹ️ определение, формулы расчета через диаметр и площадь основания, примеры нахождения объема полого цилиндра, онлайн-калькулятор

Как найти объем цилиндра? Любой грамотный человек обязан отличить радиус от диаметра, знать, что такое высота, помнить основные формулы геометрии и уметь рассчитать объем шара или куба. 

Практическое использование геометрических формул в повседневной жизни очень высоко. Рассчитать объем в кубических метрах перевозимого груза транспортной компанией, пропускную способность трубы под домом и многое другое — во всех этих и подобных им случаях поможет геометрия.

Как найти объем цилиндра

При упоминании о цилиндре на ум приходит классический головной убор. Кроме него в окружении можно встретить много разновидностей этой фигуры.

В теории — это тело, которое ограничено цилиндрической поверхностью и пересекающими её параллельными плоскостями.

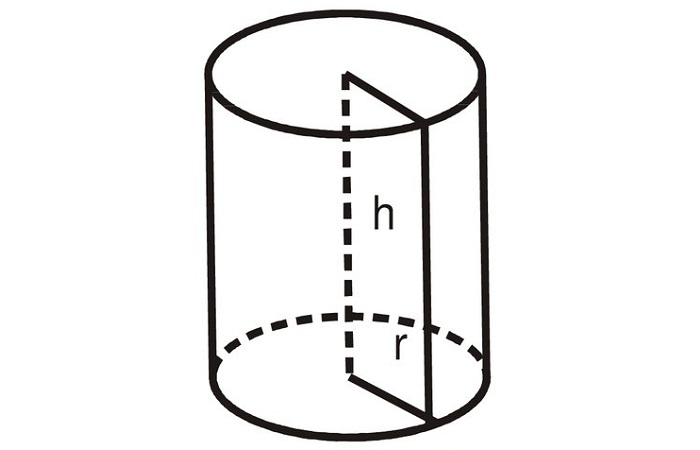
Рассчитать его объем возможно следующим образом:

V = πr²h

где 

• r – радиус;

• h – высота.

Как видите, формула проста и прозрачна, и если обывателю нужно, как вариант, определить объем цистерны воды, можно смело ее использовать. Хотя, если возникают сомнения в правильности расчетов, для этой цели можно использовать калькулятор и определить объем онлайн.

Формула объема цилиндра через диаметр

К сожалению, случается, что при расчете объема фигуры известны не все размеры. Так, например, может не быть данных о радиусе. 

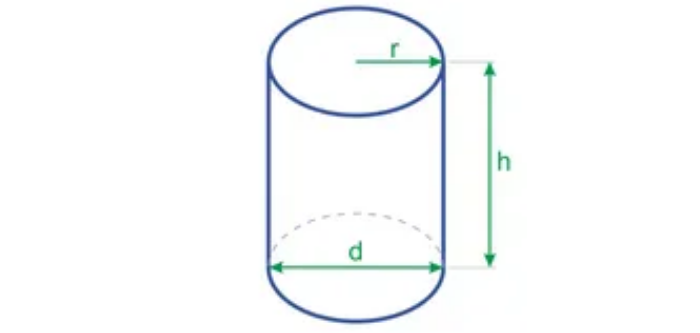
В данном случае, если знать диаметр или иметь возможность его измерить, можно воспользоваться следующей формулой:

V = 4πd²h

где 

• d– диаметр;

• h – высота.

Объем полого цилиндра

Расчет полого цилиндра нужен, когда необходимо, например, рассчитать вес полой трубы. Ее масса равна произведению плотности материала и объема.

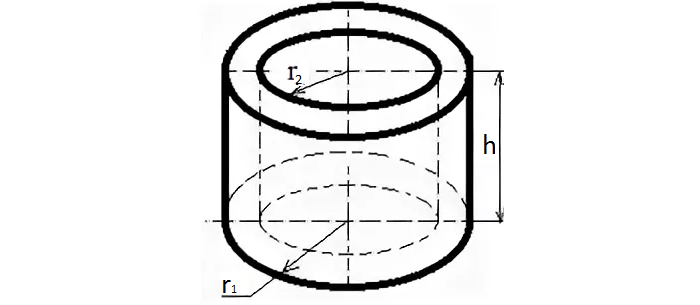
Формула для вычисления:

V = π (r₁² — r₂²)h

где 

Примеры задач с решениями

Задача №1

Высота бочки с водой равна 3 метрам, радиус составляет 0,75 метра. Рассчитать в литрах, сколько нужно жидкости, чтобы заполнить емкость наполовину?

Решение:

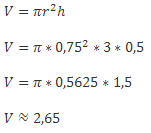
Ответ: 2,65 литров.

Задача №2

В цехе подготовили заготовку цилиндра. Диаметр основания равен высоте и составляет 20 см. Нужно найти объем заготовки.

Вычисляем:

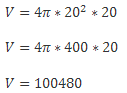
Ответ: 100480 см³.

Задача №3

На производстве нужно изготовить две трубы с двумя равными поверхностями. Внешний радиус первой трубы равен 5см, а внутренний 4 см, высота 200 см. Внутренний радиус второй равен 3 см. 

Сколько понадобится материала для изготовления труб?

Решение:

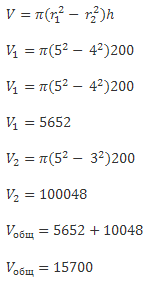
Ответ: 15700 см

3.

nauka.club

Как найти объем цилиндра — Разница Между

Цилиндр — Определение

Цилиндр является одной из основных конических форм, встречающихся в геометрии, и его свойства известны уже тысячи лет. Обычно цилиндр определяется как набор точек, которые находятся на постоянном расстоянии от отрезка, где отрезок называется осью цилиндра.

В более широком смысле цилиндр может быть определен как криволинейная поверхность, образованная отрезком линии, параллельным другому отрезку, при движении по траектории, определенной некоторым геометрическим уравнением. Это определение позволяет включать несколько других типов цилиндров, чтобы создать семейство цилиндров. Если поперечное сечение является эллипсом, цилиндр является эллиптическим цилиндром. Если поперечное сечение представляет собой параболу или гиперболу, его называют параболическим и гиперболическим цилиндрами соответственно.

 

Круглый цилиндр можно рассматривать как предельный случай n-сторонних призм, где n достигает бесконечности.

Как правило, описанная выше фиксированная линия служит осью цилиндра, и любая из плоских поверхностей называется основанием. Перпендикулярное расстояние между основаниями называется высотой цилиндра.

 

Использование формулы для определения объема цилиндра

Для общего цилиндра с базовой площадью A и высотой h объем цилиндра определяется по формуле:

В_{цилиндр}= Ах

Если цилиндр имеет круглое сечение, уравнение сводится к

V = πr² час

где r — радиус. Даже если формы цилиндров не являются правильными, то есть основания цилиндров не образуют прямые углы с криволинейной поверхностью, вышеприведенные уравнения выполняются.

Чтобы найти объем цилиндра, нужно знать две вещи,

• Высота цилиндра
• Площадь поперечного сечения —Если цилиндр имеет круглое поперечное сечение, радиус должен быть известен. Чтобы определить площадь эллиптической или параболической или гиперболической, необходима другая информация для определения площади, и необходимо провести дальнейшие вычисления.

Расчет объема цилиндра — примеры

• Внутренний радиус цилиндрического резервуара для воды составляет 3 метра. Если вода заполнена до высоты 1,5 м, найдите объем воды, включенной в бак.

Радиус основания указан как 3 м, а высота как 1,5 м. Поэтому, применяя объем цилиндра по формуле, мы можем получить объем воды в баке.

V = πr² ч = 3,14 × 3²× 1,5 = 42.39m³

• Цилиндрический топливный бак имеет диаметр 6 м и длину 20 м топлива, бак заполнен только на 80% его вместимости. Если двигатель опорожняет резервуар за 1 час 40 минут, определите среднюю объемную скорость перекачки насоса.

Чтобы определить объемную скорость перекачки насоса, необходимо определить общий откачиваемый объем. Поэтому необходимо рассчитать объем резервуара. Поскольку диаметр задан, мы можем определить радиус по формуле D = 2r. Радиус 3м. Используя формулу объема цилиндра, мы имеем

V = πr² ч = 3,14 × 3²× 20 = 565.2m³

Объем топлива внутри составляет всего 80 от общего объема, и потребовалось 100 минут, чтобы опорожнить бак, объемный расход составляет

ru.strephonsays.com

Формулы, позволяющие находить объём цилиндра в метрах и литрах

Среди множества геометрических фигур часто встречается и цилиндр. Это геометрическое тело применяется в многочисленных расчётах. Согласно принятой терминологии под таким понятием принято иметь ввиду тело геометрического типа, которое в своей основе имеет поверхность. Данная поверхность представляет также цилиндрическую форму.

В литературе данная поверхность часто именуется, как поверхность бокового вида. Кроме этого, в такой фигуре есть пара поверхностей, носящих наименование оснований. Эти основания цилиндра представляют собой окружности равного диаметра. Цилиндр, в основании которого находится круг принято считать круговым.

Ещё со школьных времён знакома всем фигура цилиндра классического типа. Это и есть круговой цилиндр.

Типы цилиндров

В математике существует несколько типов цилиндров, которые постоянно используются в геометрии.

1. Цилиндр прямого типа. Это геометрическая фигура, которая имеет прямой угол между боковой поверхностью и основаниями. Такой тип самый распространённый и часто применяется в решении большого количества задач.
2. Наклонный цилиндр. Исходя из основания фигуры, можно сделать вывод, что угол между боковой поверхностью и основаниями фигуры будет отличным от прямого. При этом он может колебаться в своём значении, как в большую, так и в меньшую сторону от прямого угла.

Вычисление объёма

Довольно часто для работы с цилиндрами требуется вычислить его объём. Это процедура в последнее время производится с применением вычислительной техники. Однако, чтобы провести такую процедуру необязательно использовать калькулятор и другие дополнительные методы решения поставленной задачи.

Сейчас существует несколько основных методов, которые позволяют произвести вычисление данного параметра. Это, по сути, универсальные формулы. Каждая из таких формул имеет свои входные параметры, отталкиваясь от которых и можно найти требуемое значение объёма. Это позволяет достигнуть ряда положительных моментов в расчётах.

1. Значительно сокращается время для осуществления операций подсчёта объёма.
2. Уменьшается вероятность того что может быть совершена ошибка в расчётах
3. Требуется для вычисления ограниченное число параметров, знание которых и даёт возможность достигать результата.

Исходные данные

Производя вычисление такого параметра, как объём, необходимо помнить, что требуется первоначальное знание параметра, который и будет исходным данным для такой процедуры.

Необходимо иметь значение высоты. Это расстояние от нижнего и верхнего основания фигуры. При этом в зависимости от типа она может определяться по-разному. В ситуации прямоугольного цилиндра высота соответствует расстоянию между основаниями фигуры. Если же он относится к наклонному типу, то расстояние будет вычисляться иным путём. Это параметр, который соответствует длине прямой проведённой под прямым углом от одного основания до плоскости, на которой лежит второе основание.

После определения такого значения можно приступать к вычислению объёма.

Методы расчёта

Существует два основных метода, которые позволяют производить вычисление такого параметра.

1. Метод вычисления объёма цилиндра на основе высоты геометрической фигуры. Этот метод является универсальным средством и может быть использован для фигур любого типа как прямоугольных, так и наклонных цилиндров. Дополнительно к значению высоты в данном способе следует знать и площадь основания. Если остановиться подробнее на данном параметре, то надо отметить что основанием является круг. Поэтому вычисление площади круга происходит на основе радиуса. Таким образом, вторым параметром в данном методе должен выступать радиус основания цилиндра. Тогда площадь определяется согласно стандартной формуле.

S= П *R^2

В данной формуле принято следующее обозначение при помощи переменных:

• П – это параметр, обозначающий соотношение между длиной и радиусом окружности, равный 3,1415928.
• R – Радиус окружности, лежащий в основании цилиндра.
• S — Площадь основания фигуры.

Вычисление непосредственно объёма цилиндра производится на основе стандартной формулы.

V=S*h

В данной формуле принято следующее обозначение при помощи переменных:

• S – Площадь основания цилиндра, имеющего форму круга.
• h – Высота геометрической фигуры.
• V – объём цилиндра.

1. Вторым методом, позволяющим произвести вычисление объёма данной фигуры, является соотношение таких параметров, как высота цилиндра и радиуса его основания. По сути, данная формула является преобразованной формулой первого метода. В ней нет разделения на промежуточные этапы подсчёта параметров. Сразу же включены все математические операции.

Таким образом, в ней одновременно производится подсчёт площади круга и объёма цилиндра.

Приведём формулу расчёта объёма цилиндра для данного метода.

V= П *R^2*h

В данной формуле принято следующее обозначение при помощи переменных:

• П – это параметр, обозначающий соотношение между длиной и радиусом окружности, равный 3,1415928.
• R – Радиус окружности, лежащий в основании цилиндра.
• h – Высота геометрической фигуры.
• V – Объём цилиндра.

Объём в литрах

Если говорить о нахождении объёма такой геометрической фигуры, то надо отметить что это задача не только для школьной программы. Используя приведенные ранее методы, есть возможность производить расчёты объёма ёмкости неизвестного типа.

К примеру, есть возможность вычислить объём ёмкости для полива на садовом участке. Однако есть и особенность при проведении подсчёта. Надо все значения подставлять в формулы в метрах. В результате проведения расчётом получается значение, которое будет измеряться в кубических метрах.

Однако, принято при расчётах поливных ёмкостей пользоваться измерениями в литрах. Для этого необходимо произвести пересчёт полученного значения объёма в литры. Это происходит на основе простого соотношения, где один кубический метр равняется 1000 литрам жидкости.

Если вычисления происходят в сантиметрах, то и результат будет в кубических сантиметрах. Тогда надо понимать, что между кубическими сантиметрами и литрами существует чёткое соотношение. Перевод происходит путём деления полученного значения объёма на 1000. После этого данные будут представлены в литрах.

Если необходимо первоначально перевести полученный в результате вычислений параметр из кубических сантиметров в кубические метры, то достаточно произвести операцию деления. Объём делится на 1000000. Это связано с тем, что кубический метр — это куб, у которого сторона равняется 100 сантиметрам. Поэтому объём в сантиметрах будет равен произведению 100*1000*100. Соответственно это будет 1000000 сантиметров кубических.

Видео

Посмотрите, как высчитать объем цилиндра и площадь его поверхности.

liveposts.ru

Формула объема цилиндра

Цилиндр – это геометрическое тело, которое имеет цилиндрическую поверхность, называемое еще как боковая поверхность цилиндра и имеет две поверхности, которые носят название оснований цилиндра. Круговым цилиндр называют, если у него в основании лежит круг.

Высота цилиндра — это отрезок, соединяющий две любые точки оснований но обязательно расположенный перпендикулярно к ним обоим.

Объем прямого цилиндра

Цилиндр — это геометрическое тело, которое сформировано вращением прямоугольника на оси, совпадающей с одним из его сторон. Слово «цилиндр» происходит от греческого слова «kylindros».

Объем цилиндра через радиус основания и высоту цилиндра

Объем цилиндра равен произведению квадрата радиуса основания, высоты цилиндра и числа пи (3.1415)

\[ \LARGE V = \pi \cdot R^{2} \cdot H \]

где:
V — объем цилиндра
π — число пи (3.1415)
R — радиус основания
H — высота цилиндра

Объем цилиндра через площадь основания и высоту цилиндра

Объем цилиндра равен произведению площади основания цилиндра на его высоту.

\[ \LARGE V = S \cdot H \]

где:
V — объем цилиндра
H — высота цилиндра
S — площадь цилиндра

Объем цилиндра через диаметр основания и высоту цилиндра

Объем цилиндра равен произведению диаметра основания и числа пи (3.1415) делённое на четыре высоты цилиндра

\[ \LARGE V = \frac {\pi \cdot D^{2} }{4 \cdot H} \]

где:
V — объем цилиндра
π — число пи (3.1415)
D — диаметр основания
H — высота цилиндра

Калькулятор объёма цилиндра

Расчет объема цилиндра онлайн

 

Входные данные

 

Радиус цилиндра r:

 

Высота цилиндра h:

 

Количество знаков после запятой в результате вычислений

1234567

Результат

В вашем браузере отключен Javascript.
Чтобы произвести расчеты, необходимо разрешить элементы ActiveX!

Не можешь написать работу сам?

Доверь её нашим специалистам

от 100 р.стоимость заказа

2 часамин. срок

Узнать стоимость

calcsbox.com

Объем полого цилиндра

Объем полого цилиндра, формулы для вычисления объема и площадей правильного полого цилиндра.

Формула вычисления объема полого цилиндра часто применяются при расчете массы полой круглой трубы. Для вычисления массы трубы, необходимо вычисленный объем трубы (полого цилиндра) умножить на плотность материала из которого изготовлена труба (цилиндр).

Расчет площади поверхностей цилиндра, иногда необходим для определения расхода материала для нанесения защитного покрытия трубы (полого цилиндра).

Объем полого цилиндра, вычисленный через внутренний и наружный радиусы

r₁ — внешний радиус

r₂ — внутренний радиус

h — высота цилиндра

… вычисление …

Площадь основания

… вычисление …

Площадь внутренней и внешней боковой поверхности

… вычисление …

Общая площадь

… вычисление …

---

Объем полого цилиндра по толщине стенки и наружному диаметру

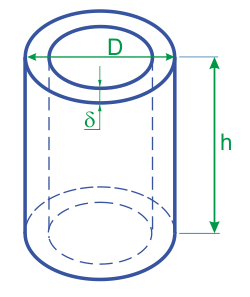
D — внешний диаметр

δ — толщина стенки

h — высота цилиндра

… вычисление …

Площадь основания

… вычисление …

Площадь внутренней и внешней боковой поверхности

… вычисление …

Общая площадь поверностей

… вычисление …

---

Объем полого цилиндра, вычисляемый по внутреннему диаметру и толщине стенки

d — внутренний диаметр

δ — толщина стенки

h — высота цилиндра

… вычисление …

Упрощение формулы:

Площадь основания

… вычисление …

Площадь внутренней и внешней боковой поверхности

… вычисление …

Упрощение формулы:

Общая площадь поверностей

… вычисление …

---

Различия между разными видами цилиндров, а также со свойствами правильного цилиндра, можно ознакомиться в статье «Объем цилиндра» в разделе« Теория».

Объем и площадь других видов цилиндров рассмотрен в статьях:

Объем цилиндра

Объем части цилиндра

Объем части полого цилиндра

---

Вы можете скачать формулы объема и площади поверхностей правильного полого цилиндра в виде картинки.

скачать скачать скачать скачать скачать скачать

doza.pro

Калькулятор объема жидкости, объема цистерны. Основание

Калибровка цистерн. Объем жидкости цистерны

Калькулятор объема жидкости, объема цистерны, массы (веса) жидкости

Объема топлива, воды, нефти, жидкгих удобрений в цистерне.
Цистерна — формы горизонтального и вертикального цилиндра. Основание — Окружность или эллипс. Объем выдается в литрах. А также: масса (вес) жидкости.


Основание

Жидкость: Вода +4CАзот жидкий -196CАзота кислотаs 25%Ацетон +20CБензинВода морскаяГлицерин +20CКеросин +20CКислота уксусная +20CМазутМасло, вазелиновое +15CМасло, креозот +20CМасло, машинное +20CМасло, парафиновое +20CМетилацетат +25CМолоко +20CНефть+20CРтуть 0CСерная кислота 95%Сероуглерод 0CСпирт, бутиловый +20CСпирт, изобутиловый +20CСпирт, изопропиловый +20CСпирт, метиловый +20CСпиртs, этиловый +20CСульфат меди (насыщ)ТерпентинУглерод жидкий -182CХлорбензол +20CХлороформ +20CЭтанол 100%Этанол 40%Этилбромид +20CЭтилиодид +20CЭтилхлорид 0CЭфир 0CДизельное топливо 20CГазовый конденсат +15,5 СБитум БНД 90/130Трансформаторное масло +20С (Первая буква)
Единица измерения: ммцмдммдюймфут
Ось A^*: Ось B:
Длина цистерны L:
Глубина жидкости H: Цена жидкости $/ед³:

Технологические карты раскроя бревен

Скорость течения жидкости в трубопроводе






www.kontroliniai.lt