Как определить объем бочки: Онлайн калькулятор объема цилиндра. Как узнать объем цилиндра.

Калькулятор расчета жидкости в бочке, цистерне, цилиндре

Инструкция для калькулятора расчета физических показателей круглой емкости

При помощи онлайн калькулятора Вы сможете правильно рассчитать объем емкости типа: цилиндра, бочки, цистерны или объем жидкости в любой другой горизонтальной цилиндрической емкости.

Определим количество жидкости в неполном баке цилиндрической формы

Все параметры указываем в миллиметрах

L — Высота бочки.

H — Уровень жидкости.

D — Диаметр бака.

Наша программа в онлайн режиме выполнит расчет количества жидкости в емкости, определит площадь поверхностей, свободную и общую кубатуру.

Как посчитать объем бочки

Для тог, чтобы правильно рассчитать вместительность резервуара для определения количества жидкости и полезной кубатуры цилиндрической емкости, необходимо определить основные параметры бака.

В нашем случае это горизонтальная цистерна.

Определение главных параметров кубатуры резервуаров (к примеру, обычная бочка или цистерна) должен производиться, основываясь на геометрическом методе расчета вместительности цилиндров. В отличие от способов калибровки емкости, где подсчет объема выполняют в виде реальных измерений количества жидкости путем мерной линейки (согласно показаниям метрштока).

V=S*L – формула расчета объема бака цилиндрической формы, где:

L — длина тела.

S — площадь поперечного сечения резервуара.

Согласно полученным результатам создают калибровочные таблицы емкости, которые еще называются тарировочными, позволяют определить вес жидкости в баке по удельному весу и объему. Эти параметры будут зависеть от уровня наполнения цистерны, который можно измерять при помощи метрштока.

Наш онлайн калькулятор предоставляет возможность выполнить расчет вместительности горизонтальных и вертикальных емкостей по геометрической формуле. Вы сможете узнать полезную вместительность резервуара более точно, если при этом правильно определите все главные параметры, которые указаны выше и участвуют в расчете.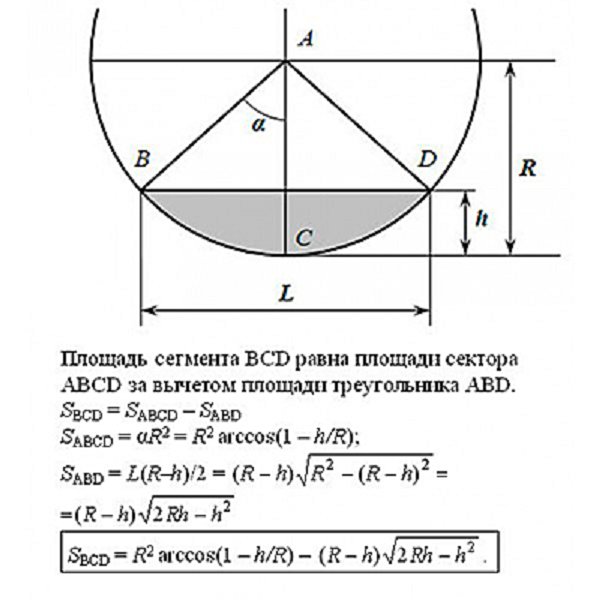

Как правильно определить основные данные

Определяем длину L

При помощи обычной рулетки, Вы сможете измерить длину L цилиндрического резервуара с неплоским дном. Для этого Вам необходимо замерить расстояние между пересекающими линиями днища с цилиндрическим телом емкости. В случае, когда горизонтальный бак с плоским дном, то для того, чтобы определить размер L, достаточно измерить длину резервуара по наружной стороне (от одного края бака до другого), и от полученного результата вычесть толщину дна.

Определяем диаметр D

Проще всего определить диаметр D бочки цилиндрической формы. Для этого достаточно при помощи рулетки замерять расстояние между двумя любыми крайними точками крышки или края.

Если трудно правильно выполнить расчет диаметра емкости, то в этом случае можно использовать измерение длины окружности. Для этого при помощи обычной рулетки обхватываем по окружности весь резервуар.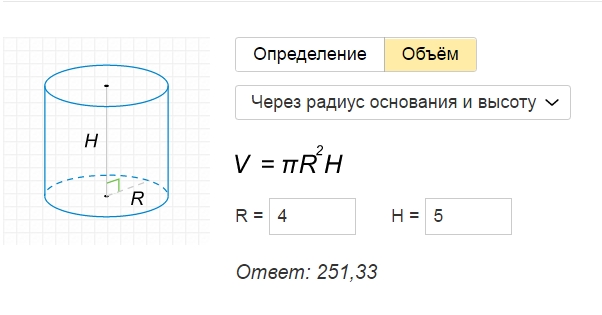

Для правильно расчета окружности делают два измерения в каждом сечении резервуара. Для этого поверхность, измеряемая должна быть чистой. Узнав усредненную длину окружности нашей емкости – Lокр, переходим к определению диаметра по следующей формуле:

d=Lокр/3,14

Этот метод наиболее простой, так как зачастую измерение диаметра бака сопровождается рядом затруднений, связанных с нагромождением на поверхности различного вида оборудования.

Важно! Измерения диаметра правильней всего выполнить в трех разных сечениях емкости, и после этого выполнить подсчет среднего значения. Так как зачастую, эти данные могут существенно отличаться.

Усредненные значения после трех замеров позволяют минимизировать погрешность расчета объема резервуара цилиндрической формы. Как правило, используемые накопительные баки во время эксплуатации подвергаются деформации, могут терять прочность, уменьшаться в размерах, что ведет к уменьшению количества жидкости внутри.

Определяем уровень H

Чтобы определить уровень жидкости, в нашем случае это H, нам понадобиться метршток. При помощи этого измерительного элемента, который опускают на дно емкости, мы сможем точно определить параметр H. Но эти расчеты будут верны для резервуаров с плоским дном.

В результате подсчета онлайн калькулятора мы получаем:

• Свободный объем в литрах;
• Количество жидкости в литрах;
• Объем жидкости в литрах;
• Общую площадь резервуара в м²;
• Площадь дна в м²;
• Площадь боковой поверхности в м².

Как найти объем бочки

Современному человеку трудно понять, почему старинные бочки имели именно такую «пузатую» форму. Дело тут не в изысках древних дизайнеров. В принципе, для этого подошли бы и емкости усеченно-конической формы – и собирать легче и объем такой бочки найти нетрудно. Однако вряд ли бы такую бочку удалось далеко укатить…Вам понадобится

Прежде чем вычислять объем бочки, внимательно осмотрите ее. Современные бочки, как правило, изготавливаются промышленным способом. Поэтому они имеют стандартный объем, который наверняка где-нибудь указан. Емкость бочки (или ее содержимого) также можно найти в сопроводительных документах (накладных, счет-фактурах и т.п.).

В некоторых случаях объем проще определить экспериментально. Для этого возьмите ведро известной емкости и просто наполните бочку водой, сосчитав количество ведер. Если некоторая часть воды из последнего ведра не уместится в бочку, измерьте объем «лишней» воды литровой банкой и вычтите из общего объема, полученного при измерении ведрами.

Большинство современных металлических и пластиковых бочек имеют цилиндрическую форму. Чтобы найти объем такой бочки, измерьте ее высоту и диаметр. Постарайтесь измерить именно внутренний диаметр бочки, если вас интересует вместимость бочки, а не то, сколько места бочка займет в погребе. После чего, умножьте высоту бочки (в метрах) на квадрат диаметра (в метрах), затем умножьте на число «пи» (примерно, 3,14) и разделите на 4.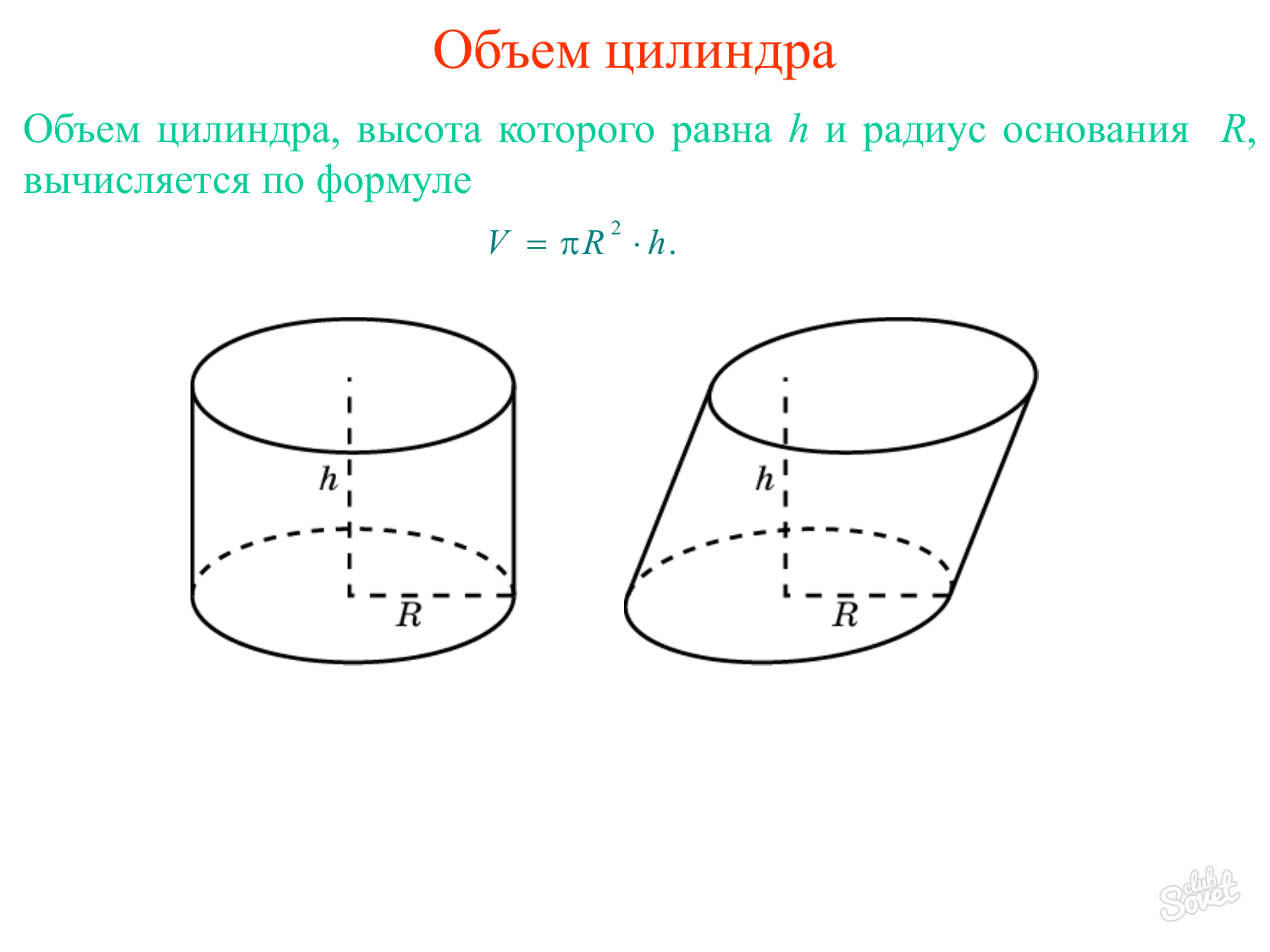 Если бочек много, заранее разделите «пи» на 4 и умножайте полученный коэффициент на высоту и квадрат диаметра. В виде формулы это правило будет выглядеть следующим образом:Vцб = π/4 * D² * Hили Vцб ≈ 0,785 * D² * H,где:Vцб – объем цилиндрической бочки,D – внутренний диаметр дна/крышки бочки.π – число «пи», примерно равное 3,14.

Для измерения диаметра бочки возьмите бечевку и зафиксируйте один из ее концов на краю бочки. Затем отыщите на противоположном краю бочки самую удаленную точку и отметьте ее на бечевке (например, завяжите узелок). Измерьте длину бечевки с помощью рулетки или линейки. Результат запишите в метрах, в виде десятичной дроби. При измерении высоты бочки проблем возникнуть не должно. Однако учтите, что некоторые бочки имеют «приподнятое» дно, поэтому измерить необходимо именно внутреннюю высоту бочки.

Если на крышке бочки каким-либо образом указан ее центр (например, в центре находится отверстие для слива), то вместо диаметра измерьте радиус бочки. Формула для расчета объема бочки в этом случае будет аналогичной:Vцб = π * R² * H,где:R – радиус дна/крышки бочки,

Если ни диаметр, ни радиус бочки измерить невозможно (например, бочки стоят в несколько «этажей»), то определите ее «обхват» . Для этого возьмите бечевку и обмотайте ее вокруг бочки.Так как длина окружности вычисляется по формуле:L = π * D, где: L – обхват (длина окружности) бочки,тодиаметр бочки будет равняться длине окружности, поделенной на π:D = L / π.Отсюда получается несложная формула:Vцб = L²/4π * Hили Vцб = L²/12,566 * H,

Чтобы найти объем настоящей деревянной бочки, воспользуйтесь практической формулой, которую применяет большинство виноделов:Vкб = 3,2 * r * R * H,где:Vкб – объем классической бочкиr – радиус дна/крышки бочки, R – радиус самой широкой части (середины) бочки.

Так как измерить радиус широкой части бочки довольно проблематично, то лучше воспользоваться формулой:Vкб = 0,8 * d * D * H.где:d – диаметр дна/крышки бочки, D – диаметр самой широкой части (середины) бочки.

Вычисление объема цилиндра

Цилиндр это геометрическое тело, которое сформировано вращением прямоугольника на оси, совпадающей с одним из его сторон. Слово «цилиндр» происходит от греческого слова «

kylindros».

Вычисление объема цилиндра

Формула расчёта объема цилиндра

 

Вычисление объема цилиндра производится по следующей формуле:

 

V = π r2h

 

V – объем цилиндра

h – высота цилиндра

r – радиус основания

π – 3.14

Как рассчитать объем цилиндра, все мы проходили в средней школе, и этими знаниями наиболее активно пользуются в своей работе конструкторы различных машин и механизмов, потребительских товаров, а также архитекторы.

Инженерам приходится производить расчет объема цилиндра в тех случаях, когда они занимаются проектированием заданий, снабженных колоннами. Правда, в последнее время эти архитектурные элементы в их, так сказать, «классическом» варианте (то есть вместе с базой и капителем) встречаются достаточно редко, но их «упрощенные» разновидности, состоящие из одного ствола (который, собственно говоря, и представляет собой цилиндр) используются весьма широко. Нередко с колоннами приходится иметь дело реставраторам различных сооружений, имеющих большую историческую и культурную ценность, правда, в их работе вычисление объема цилиндра – далеко не самая распространенная процедура. Впрочем, если речь идет о полном восстановлении утраченных по тем или иным причинам колонн, то ее также приходится производить.

Расчет объема цилиндра осуществляется тогда, когда ведётся разработка разнообразных емкостей соответствующей формы. В качестве наглядного примера таковых можно привести, скажем, медицинские шприцы, а также колбы термосов. Следует заметить, что в первом случае такой параметр, как объем, имеет очень важное значение, поскольку от него зависит точное количество медикаментов, вводимого пациенту при инъекциях.

В технике цилиндры распространены чрезвычайно широко: достаточно сказать, что их форму имеют практически все валы и их отдельные составные части, используемые, скажем, в двигателях внутреннего сгорания. К тому же, расчет объема цилиндра – одна из важнейших задач, которую приходится решать конструкторами при проектировании современных бензиновых и дизельных силовых агрегатов, ведь от этого параметра зависит множество их характеристик, и в первую очередь такая важнейшая, как мощность. Почти все типы ДВС снабжаются поршнями, которые также имеют цилиндрическую форму

.

Чрезвычайно распространенными деталями, которые присутствуют в конструкции многих сложных технических устройств, являются роликовые подшипники. Как нетрудно догадаться по самому их названию, одними из основных их компонентов являются прочные и износостойкие металлические ролики, имеющие цилиндрическую форму. Именно благодаря такой геометрии, эти детали имеют достаточно большую несущую способность и в большинстве случаев способны выдерживать весьма значительные нагрузки, чем их шариковые аналоги. Роликовые подшипники являются высокоточными деталями, и поэтому при их разработке и проектировании правильный расчет объема цилиндра (в данном случае – ролика) играет немаловажную роль.

Объем жидкости в цилиндрической таре

Ага, сегодня я путем несложных умозаключений буду выяснять объем жидкости, находящейся в цилиндрической таре, лежащей на боку.
И это не праздности ради, а дела для.

Цитирую запрос пользователя объем сегмента цилиндра (2):
Доброго времени суток. Видел калькулятор объема сегмента цилиндра, но нужно немножко другое. По работе приходится измерять количество жидкости в таре. Так вот допустим тара цилиндрической формы R=1,13м и H=6,3м лежит на поверхности. Жидкости в таре 0,9м от поверхности. Вопрос: какой объем жидкости в таре?

Там дальше в запросе идут ссылки на решение, но это же не спортивно, поэтому я пошел своим путем 🙂 Сразу замечу, что вторая, более сложная задача — объем жидкости в таре, лежащей под наклоном, еще ждет своего решения.

Вот калькулятор, который все считает, а ход рассуждений, как обычно, под ним.

Объем жидкости в цилиндрической таре

Точность вычисления

Знаков после запятой: 2

Объем жидкости

 

Процентов от общего объема

 

Общий объем цилиндра

 

content_copy Ссылка save Сохранить extension Виджет

Итак, сформулируем задачу наглядно, и посмотрим на цилиндр в разрезе (см. рисунок). Если уровень жидкости m больше половины, то находим объем воздуха в оставшейся части, а потом вычитаем из общего объема — т. е. всегда сводим к случаю, изображенному на рисунке.

Формула объема всего цилиндра известна — площадь основания, помноженная на высоту.

А нам, значит, надо найти площадь фигуры, залитой синей жидкостью, и тоже помножить на высоту. Пытливый взгляд отметит, что фигура, залитая синей жидкостью, получается из сектора после вычета верхнего треугольника.

Площадь сектора находится как
, где альфа — это угол дуги в радианах.

Угол дуги нам неизвестен. Разберемся сначала с ним. Линия, опущенная вертикально вниз делит верхний треугольник на два прямоугольных треугольника. Гипотенуза у них равна R, а катет, прилежащий к верхнему углу, равен R-m. Таким образом,

соответственно

и ответ нам Javascript даст как раз в радианах, то что нам нужно.

Теперь разберемся с верхним треугольником. Он равнобедренный, бедра равны R, а основание нам неизвестно. Найдем его.
А оно как раз равно удвоенному противолежащему катету, который, согласно всем известной теореме Пифагора равен

Зная все стороны треугольника, нетрудно найти его площадь по формуле Герона — Расчет площади треугольника по формуле Герона.

где

Вот, собственно, и все. Мы знаем площадь сектора и площадь треугольника. Вычитаем площадь треугольника из площади сектора, домножаем на высоту цилиндра (или длину цилиндра, с учетом того, что он лежит) и получаем результат.

Как посчитать объем цилиндра — онлайн калькулятор

Чтобы посчитать объем цилиндра воспользуйтесь нашим удобным онлайн калькулятором:

Онлайн калькулятор

Найти чему равен объем цилиндра (V) можно зная (либо-либо):

• радиус r и высоту h цилиндра
• диаметр d и высоту h цилиндра
• площадь основания S_o и высоту h цилиндра
• площадь боковой поверхности S_b и высоту h цилиндра

Подставьте значения в соответствующие поля и получите результат.

Зная радиус r и высоту h

Чему равен объем цилиндра V если известны его радиус r и высота h?

Формула

V = π⋅r²⋅h

Пример

Если цилиндр имеет высоту h = 8 см, а его радиус r = 2 см, то:

V = 3.14156 ⋅ 2² ⋅ 8 = 3.14156 ⋅ 32 = 100.53 см³

Зная диаметр d и высоту h

Чему равен объем цилиндра V если известны его диаметр d и высота h?

Формула

V = π⋅(^d/₂)²⋅h

Пример

Если цилиндр имеет высоту h = 5 см, а его диаметр d = 1 см, то:

V = 3.14156 ⋅ (¹/₂)² ⋅ 5 = 3.14156 ⋅ 1.25 ≈ 3.927 см³

Зная площадь основания S

_o и высоту h

Чему равен объем цилиндра V если известны его площадь основания S_o и высота h?

Формула

V = S_o⋅h

Пример

Если цилиндр имеет высоту h = 10 см, а площадь его основания S_o = 5 см², то:

V = 10 ⋅ 5 = 50 см³

Зная площадь боковой поверхности S

_b и высоту h

Чему равен объем цилиндра V если известны его площадь боковой поверхности S_b и высота h?

Формула

V = ^S_b2/_4πh

Пример

Если цилиндр имеет высоту h = 5 см, а площадь его боковой поверхности S_b = 30 см², то:

V = ³⁰²/ _{4 ⋅ 3. 14⋅ 5} = ⁹⁰⁰/_62.8 = 14.33 см³

См. также

Расчет объема жидкости в горизонтальной цилиндрической емкости. Бондарное ремесло. Зависимость размеров бочки и клепки от необходимого объема бочки; как измерить объем бочки

Многие строительные материалы, топливо, пищевые продукты поступают на оптовые базы в емкостях цилиндрической или близкой к ним формы. Это могут быть бочки, цистерны или бидоны. Во всех подобных случаях для определения количества вещества необходимо сначала вычислить объем. Форма таких емкостей может несколько отличаться от классического цилиндра, поэтому и методы расчетов будут отличаться.

Вам понадобится

Инструменты для измерения длины;
— калькулятор.

Спонсор размещения P&G Статьи по теме «Как рассчитать объем бочки» Как складывать квадратные корни Как найти диагональ квадрата Как найти координаты вершины параболы

Инструкция

Бочка может иметь правильную цилиндрическую форму. В этом случае ее основание представляет собой круг. Если есть возможность, найдите центр основания, проведите через него диаметр и измерьте. Разделите его на 2. Получится радиус. Это можно сделать у лежащей на боку или перевернутой бочки. Когда такой возможности нет, измерьте длину окружности основания и найдите радиус по формуле R=P/2?, где R – радиус основания, а P – длина окружности.

Измерьте высоту бочки. Это легче всего сделать рулеткой. Для точности начертите на боку линию, которая будет строго перпендикулярна основанию. Вычислите объем бочки по той же формуле, что и объем любого другого цилиндра. V=?*R2*H, где V – объем, R – радиус основания бочки, H – высота.

Основание бочки не обязательно являет собой окружность, а боковая поверхность может быть изогнутой. В этом случае вам необходимо сделать еще несколько измерений. Если ее бока изогнуты по параболе или по дуге круга, вычислите или замерьте еще диаметр среднего сечения. Обозначьте диаметр основания как D», а площадь среднего сечения как D»».

Объем бочки, боковая поверхность которой изогнута по дуге круга, вычислите, умножив число? на 1/12 высоты и на сумму удвоенного квадрата диаметра среднего сечения и квадрата основания. Это можно выразить формулой V=?*H/12*(2D»»2+D»2), где H – высота, D» и D»» — соответственно диаметры основания и среднего сечения, а V – объем.

По похожему принципу вычисляется и объем бочки, боковая поверхность которой изогнута по параболе. Он равен произведению числа? на 1/15 высоты и на сумму удвоенного квадрата диаметра основания, произведения обоих диаметров и 0, 75 квадрата диаметра основания). Это действие может быть обозначено формулой V=?*H/15*(2D»»2+D»*D»»+0,75D»2).

Как просто

Другие новости по теме:

В наше время уже редко где можно встретить настоящую деревянную бочку. Место классических бочек давно заняли их металлические и пластиковые аналоги. Как правило, современные бочки имеют форму цилиндра, поэтому вычислить объем такого сосуда очень просто. А вот посчитать вместимость старинной,

Чтобы вычислить объем любого тела, нужно знать его линейные размеры. Это касается таких фигур как призма, пирамида, шар, цилиндр и конус. Для каждой из этих фигур есть своя формула определения объема. Вам понадобится — линейка; — знание свойств объемных фигур; — формулы площади многоугольника.

В наше время уже редко где можно встретить настоящую деревянную бочку. Место классических бочек давно заняли их металлические и пластиковые аналоги. Как правило, современные бочки имеют форму цилиндра, поэтому вычислить объем такого сосуда очень просто. А вот посчитать вместимость старинной, «пузатой», бочки сможет далеко не каждый математик.

Вам понадобится

линейка, калькулятор, веревка

Спонсор размещения P&G Статьи по теме «Как вычислить объем бочки» Как найти массу цилиндра Как определить объем тела, образованного вращением Как вычислить объем конуса

Инструкция

Если бочка имеет цилиндрическую форму, то измерьте ее высоту и радиус. Для толстостенной необходимо измерить именно внутренний радиус, чтобы получить ее вместимость, а не просто занимаемый объем. Переведите результаты измерений в метры. Затем воспользуйтесь классической формулой для вычисления объема цилиндра:

Vцил = ? * R? * H,

R – радиус основания (дна) бочки,
Н – высота бочки,
Vцил – объем цилиндрической бочки,
? – число «пи», примерно равное 3,14.

Если радиус бочки измерить затруднительно, то измерьте ее диаметр. Для этого зафиксируйте один конец линейки или веревки на краю бочки. Затем, поворачивая линейку или веревку, найдите самую удаленную точку на противоположном краю. Так как диаметр бочки в два раза больше ее диаметра, то формула для вычисления объема бочки будет аналогичной:

Vцил = ? * (D/2)? * H,

Vцил = ? * ? * D? * H,

где: D – внутренний диаметр дна бочки.

Если и диаметр бочки измерить невозможно, то определите длину ее окружности. Для этого возьмите достаточно длинную веревку (шнур, бечевку, нитку и т.п.) и обмотайте ее один раз вокруг бочки.

Так как длина окружности равна? * D, то диаметр бочки будет равен длине ее окружности, разделенной на?. Т.е. D = L / ?. Чтобы определить объем бочки через длину окружности, подставьте это выражение в предыдущую формулу:

Vцил = ? * ? * D? * H = ? * ? * (L/?)? * H = ? * L?/? * H,

где: L – длина окружности (обхват) бочки.

Если нужно вычислить объем классической (пузатой) бочки, то не стоит изучать сочинение Кеплера «Стереометрия винных бочек». Просто воспользуйтесь чисто практической формулой, выведенной за несколько столетий виноделами Франции:

Vб = 3,2 * r * R * H,

r – радиус дна бочки, а

R – радиус ее самой широкой части.

Соответственно, если известны только диаметры дна (d) и середины (D) бочки, то воспользуйтесь формулой:

Vб = 0,8 * d * D * H.

Как просто

Другие новости по теме:

Современному человеку трудно понять, почему старинные бочки имели именно такую «пузатую» форму. Дело тут не в изысках древних дизайнеров. В принципе, для этого подошли бы и емкости усеченно-конической формы – и собирать легче и объем такой бочки найти нетрудно. Однако вряд ли бы такую бочку удалось

Кубический метр (кубометр) — это мера объема, принятая к использованию в международной метрической системе единиц измерений. То есть, для определения количества кубометров какого-либо материала (например, бетона, газа, древесины и т.д.) следует вычислить занимаемый им объем. В зависимости от

В наше время уже редко где можно встретить настоящую деревянную бочку. Место классических бочек давно заняли их металлические и пластиковые аналоги. Как правило, современные бочки имеют форму цилиндра, поэтому вычислить объем такого сосуда очень просто. А вот посчитать вместимость старинной, «пузатой», бочки сможет далеко не каждый математик.

Вам понадобится

• линейка, калькулятор, веревка

Инструкция

• Если бочка имеет цилиндрическую форму, то измерьте ее высоту и радиус. Для толстостенной необходимо измерить именно внутренний радиус, чтобы получить ее вместимость, а не просто занимаемый объем. Переведите результаты измерений в метры. Затем воспользуйтесь классической формулой для вычисления объема цилиндра:Vцил = π * R² * H,где:R – радиус основания (дна) бочки,
  Н – высота бочки,
  Vцил – объем цилиндрической бочки,
  π – число «пи», примерно равное 3,14.
• Если радиус бочки измерить затруднительно, то измерьте ее диаметр. Для этого зафиксируйте один конец линейки или веревки на краю бочки. Затем, поворачивая линейку или веревку, найдите самую удаленную точку на противоположном краю. Так как диаметр бочки в два раза больше ее диаметра, то формула для вычисления объема бочки будет аналогичной:Vцил = π * (D/2)² * H,или:Vцил = ¼ * π * D² * H,
  где: D – внутренний диаметр дна бочки.
• Если и диаметр бочки измерить невозможно, то определите длину ее окружности. Для этого возьмите достаточно длинную веревку (шнур, бечевку, нитку и т.п.) и обмотайте ее один раз вокруг бочки.
  Так как длина окружности равна π * D, то диаметр бочки будет равен длине ее окружности, разделенной на π. Т.е. D = L / π. Чтобы определить объем бочки через длину окружности, подставьте это выражение в предыдущую формулу:Vцил = ¼ * π * D² * H = ¼ * π * (L/π)² * H = ¼ * L²/π * H,где: L – длина окружности (обхват) бочки.
• Если нужно вычислить объем классической (пузатой) бочки, то не стоит изучать сочинение Кеплера «Стереометрия винных бочек». Просто воспользуйтесь чисто практической формулой, выведенной за несколько столетий виноделами Франции:Vб = 3,2 * r * R * H,где:r – радиус дна бочки, а
  R – радиус ее самой широкой части.Соответственно, если известны только диаметры дна (d) и середины (D) бочки, то воспользуйтесь формулой:Vб = 0,8 * d * D * H.

Определение объема деревянных бочек

Бочки бывают весьма разнообразной формы как в длину, так и в ширину. Существует несколько способов приблизительного определения объема бочек. Приведем некоторые из них.

1. Если клепки бочки имеют форму эллипса, то ее объем будет равен сумме объемов трех конусов, имеющих высоту, равную высоте бочки; основания двух из этих конусов равны площади наибольшего поперечного сечения бочки; основание третьего конуса равно площади дна бочки.

2. Если высоту бочки обозначить буквой h, диаметр наибольшего сечения бочки — буквой D, диаметр дна — буквой d, то объем бочки V можно определить по формуле:

V=hπ(2D²+d):12.

3. Измеряют диаметр наибольшего поперечного сечения бочки и диаметр ее дна. Второе число вычитают из первого и к диаметру дна прибавляют 2/3 полученной разности (если бочка очень выпуклая) или 1/2 этой разности, (если бочка менее выпуклая). Полученное число считают средним диаметром бочки. Квадрат этого числа умножают на коэффициент 0,7854 и на высоту бочки. Полученное произведение и будет приблизительным объемом бочки.

Так, предположим, что наибольший диаметр² бочки равен 18 дюймам, диаметр дна — 12 дюймам (*** 1 дюйм = 2,54см, 1 фут = 12 дюймов = 30,48 см.). Значит, разноcть составит 6 дюймов. Прибавим 2/3 этой разности к диаметру дна, получим 16 дюймов (40,6 см). Это число и примем за средний диаметр бочки. Далее возведем 16 в квадрат: 16х16=256. Умножим это число на 0,7854, получим 201,0624. Теперь умножаем полученный результат на высоту бочки (предположим, что высота бочки составляет 4 фута=48 дюймов): 201,0624х48=9651 кубических дюймов (или 152 л).

Иногда требуется определить объем жидкости, наполняющей лишь часть бочки. В таких случаях поступают следующим образом.

Бочку кладут на бок, т.е. на одну из боковых клёпок. На половине ее длины делают небольшое отверстие, через которое пропускают тоненькую, но твердую несгибающуюся палочку. Конец палочки должен коснуться врутренней стороны боковой нижней клепки, на которой лежит бочка.

Затем, вынув палочку, измеряют глубину жидкости Н, находят отношение этой глубины к диаметру поперечного сечения бочки D в том месте, где определялась глубина жидкости, и полученное отношение умножают на объем всей бочки и на особый коэффициент к, который приведен ниже.

Таблица 1. Значение коэффициента к (отношение глубины жидкости Н к диаметру поперечного сечения бочки D)

H/D	k	H/D	k	H/D	k	H/D	k
1,0	1,000	0,75	0,846	0,5	0,500	0,25	0,184
0,95	0,989	0,7	0,757	0,45	0,433	0,2	0,130
0,9	0,960	0,65	0,697	0,4	0,368	0,15	0,081
0,85	0,919	0,6	0,632	0,35	0,303	0,1	0,040
0,8	0,870	0,55	0,567	0,3	0,243	0,01	0,001

Ствол — Калькулятор геометрии

1D линия, круговая дуга, парабола, спираль, кривая Коха 2D правильных многоугольников: равносторонний треугольник, квадрат, пятиугольник, шестиугольник, семиугольник, восьмиугольник, девятиугольник, десятиугольник, шестиугольник, додекагон, шестиугольник, N-угольник, многоугольник кольцо другие многоугольники: треугольник, прямоугольный треугольник, равнобедренный треугольник ИК-треугольник, четырехугольник, прямоугольник, золотой прямоугольник, ромб, параллелограмм, полуквадратный воздушный змей, воздушный змей, воздушный змей, правая трапеция, равнобедренная трапеция, треугольная равносторонняя трапеция, трапеция, циклический четырехугольник, тангенциальный четырехугольник, стрелка, вогнутый четырехугольник, крест Антипараллелограмм, Форма дома, Симметричный пятиугольник, Вырезанный прямоугольник, Вогнутый пятиугольник, Вогнутый правильный пятиугольник, Параллелогон, Вытянутый шестиугольник, Вогнутый шестиугольник, Стрелка-шестиугольник, Прямоугольный шестиугольник, L-образная форма, Острый перегиб, T-образная форма, Усеченный квадрат, Рамка, Открытая рамка, сетка, крест, форма X, форма H, тройная звезда, четыре звезды, пентаграмма, гексаграмма, уникурсальная гексаграмма, октаграмма, звезда Лакшми, двойная звезда многоугольник, многоугольник, многоугольник 90 004 Круглые формы: Круг, Полукруг, Круговой сектор, Круговой сегмент, Круговой слой, Круговой центральный сегмент, Круглый угол, Круглый угол, Круговая касательная стрелка, Форма капли, Полумесяц, Остроконечный овал, Ланцетная арка, Бугорок, Кольцо, Кольцевой сектор , Изогнутый прямоугольник, закругленный многоугольник, закругленный прямоугольник, эллипс, полуэллипс, эллиптический сегмент, эллиптический сектор, эллиптическое кольцо, стадион, спираль, бревно.Спираль, Треугольник Рело, Циклоида, Двойная Циклоида, Астроид, Гипоциклоида, Кардиоида, Эпициклоида, Параболический сегмент, Сердце, Треугольник, Межугловой треугольник, Круговой треугольник дуги, Четырехугольник Interarc, Межкруговый четырехугольник, Круговой четырехугольник дуги, Круговой дуговый многоугольник, Коготь, Коготь — Ян, Арбелос, Салинон, Выпуклость, Луна, Три круга, Поликруг, Многоугольник с закругленными краями, Роза, Шестеренка, Овал, Профиль яйца, Лемниската, Сквикул, Круговой квадрат, Дигон, Сферический треугольник 3D Платоновых тел: тетраэдр, куб, октаэдр, додекаэдр, икосаэдр архимедова Solids: усеченный тетраэдр, кубооктаэдр, усеченный куб, усеченный октаэдр, ромбокубооктаэдр, усеченный кубооктаэдр, икосододекаэдр, усеченный додекаэдр, усеченный икосаэдр, Snub куб, ромбоикосододекаэдр , Усеченный икосододекаэдр, Snub Додекаэдр Каталонских Сухой остаток: триакистетраэдр, ромбический додекаэдр, триакисоктаэдр, тетракисгексаэдр, дельтоидальный икоситетраэдр, гексакис октаэдр, ромбический триаконтаэдр, триакисикосаэдр, пентакисдодекаэдр, Пятиугольные Icositetrahedron, дельтоидальный гексеконтаэдр, гексакис Икосаэдр, Пятиугольный гексеконтаэдр Твердые тела Джонсона: Пирамиды, купола, ротонда, удлиненные пирамиды, гиро-продолговатые пирамиды, бипирамиды, удлиненные бипирамиды, гиро-продолговатая квадратная дипирамида, гиробифастигениум, дисфагениум Sphenocorona, Disphenocingulum Другие многогранники: Кубоид, квадратный столб, треугольная пирамида, квадратная пирамида, правильная пирамида, пирамида, правильная пирамида, конус, правильная бипирамида, бипирамида, бифрустум, клин-фрустум, клин-фрустум Полутетраэдр, ромбоэдр, параллелепипед, правильная призма, призма, наклонная призма, антикуб, антипризма, призматоид, трапецоэдр, дисфеноид, угол, общий тетраэдр, клин-кубоид, полукубоид, скошенный кубоид, слиток, скошенная трехгранная призма , Усеченный кубоид, кубоид с тупыми краями, удлиненный додекаэдр, усеченный ромбоэдр, обелиск, изогнутый кубоид, полый кубоид, полая пирамида, полая пирамида, звездная пирамида, звездчатый октаэдр, малый звездчатый додекаэдр, большой звездчатый додекаэдр70004, большой додекаэдр70004 Круглые формы: сфера, полусфера, сферический угол, цилиндр, отрезной цилиндр, наклонный цилиндр, изогнутый цилиндр, эллиптический цилиндр, обобщенный Цилиндр, конус, усеченный конус, косой круговой конус, эллиптический конус, биконус, усеченный биконус, заостренный столб, закругленный конус, капля, сфероид, эллипсоид, полуэллипсоид, сферический сектор, сферическая крышка, сферический сегмент, сферический центральный сегмент, двойной калотт , Сферический клин, полуцилиндр, диагонально разрезанный пополам цилиндр, цилиндрический клин, цилиндрический сектор, цилиндрический сегмент, цилиндр с плоским концом, полуконус, конический сектор, конический клин, сферическая оболочка, полусферическая оболочка, цилиндрическая оболочка, цилиндрическая оболочка с вырезом, косо-цилиндрическая оболочка , Полый конус, усеченный полый конус, сферическое кольцо, тор, шпиндельный тор, тороид, сектор тора, сектор тороида, арка, тетраэдр Рело, капсула, сегмент капсулы, двойная точка, антиконус, усеченный антиконус, сферический цилиндр, линза, вогнутый Линза, ствол, форма яйца, параболоид, гиперболоид, олоид, твердые тела Штейнмеца, твердое тело вращения 4D Тессеракт, Гиперсфера

Anzeige Расчеты на бочке.Геометрически ствол представляет собой усеченный вытянутый сфероид с кругами одинакового размера сверху и снизу. Формула объема ствола была открыта Иоганном Кеплером. Площадь поверхности слегка изогнутой бочки близка к площади цилиндра с радиусом R. Введите радиус и высоту и выберите количество десятичных знаков. Затем нажмите Рассчитать. Формулы: d = √ h² + (2 * r) ² V = π * h * (2R² + r²) / 3 pi: π = 3,141592653589793… Радиусы, высота и диагональ имеют одну и ту же единицу измерения (например, метр), объем имеет эту единицу с точностью до трех (например, кубический метр). Доля: © Jumk.de Webprojects Anzeige

Баррели нефти — Math Central

Привет Дэрил,

В теме вашего электронного письма говорилось о баррелях нефти, и это важно, поскольку баррель — это единица объема и в других ситуациях, а баррели не все одинакового размера. Баррель нефти составляет 42 галлона США.

Я использовал наш калькулятор объема с диаметром 15,5 футов и высотой 1 дюйм и получил объем 117,63 галлона США. Поскольку в барреле нефти 42 галлона, то это $ \ large \ frac {117.63} {42} \ normalsize = 2.801 \ mbox {barrels.} $. Это означает, что $ \ large \ frac {180} {2.801} \ normalsize = 64,27 $ дюйма даст 180 баррелей.

Я бы проверил, что диаметр резервуара на самом деле составляет 15 футов 6 дюймов, поскольку резервуар с таким диаметром и высотой 16 футов содержит 537,7 баррелей, а не 500.

Харлей

В мае 2014 года Дэрил снова отправил свой вопрос

Вопрос от Дэрил:

Я пытаюсь выяснить, сколько баррелей нефти на дюйм высоты в резервуаре на 500 баррелей, 16 футов высотой и пятнадцать футов шесть дюймов в диаметре. (Номинальный диаметр)
Я уверен, что это цифры. Они указаны на заводской табличке, прикрепленной к резервуару. Я получил один ответ: 500 / (16×12) = 2,604, и в этом случае, если бы я хотел загрузить 1800 бочек, мне нужно было потянуть 5 футов 9 дюймов за 179.676 баррелей.
Другая формула гласит, что номинальный диаметр резервуара должен составлять 15 футов 5 дюймов, иначе это будет 537 баррелей, а не 500, а 2,8 барреля на дюйм. Я уверен насчет 500 и 15 футов 6 дюймов. Я видел много ответов, но ни один из них не был окончательным. Большое спасибо!

Дэрил,

Путаница возникает из-за того, что изготовители резервуаров используют термин номинальный. Согласно онлайн-словарю Merriam Webster, термин номинальный означает «существующее как нечто только по названию: не действительное или реальное».Если вы прокрутите страницу сайта Merriam Webster, чтобы просмотреть полное определение, вы увидите 3b , в котором говорится, что «является или относится к назначенному или теоретическому размеру, который может отличаться от фактического: приблизительный <номинальный размер трубы> «.

В вашем исходном вопросе у вас было «Номинальный диаметр — 15 футов 6 дюймов, номинальная высота — 16 футов, номинальная вместимость — 500 баррелей». Если это то, что напечатано на табличке с данными производителя, то я ничем не могу вам помочь, поскольку вы не знаете никаких реальных размеров.

Харлей

Комментарий от Бена

В марте 2019 года мы получили этот комментарий от Бена.

Это не совсем вопрос. Это скорее прямой ответ для автоперевозчика, который написал, задаваясь вопросом о количестве дюймов для своего груза 180 баррелей нефти. Поскольку все масляные резервуары немного отличаются, номинальный диаметр, который он использовал (15 футов 6 дюймов), хотя и является приемлемым, не дает ответа по всем направлениям. Однако, чтобы продать резервуар из резервуара, он должен быть пристегнут ремнями. — то есть его объем должен быть рассчитан с шагом 1/4 дюйма высоты.Таким образом, чтобы определить количество дюймов для нагрузки 180 баррелей, лучше всего начать с таблицы обвязки для этого конкретного резервуара. Кроме того, следует помнить, что, поскольку масло очень летучее, его объем очень зависит от температуры, поэтому эквивалентный объем при стандартной температуре уменьшается с понижением температуры (и наоборот). Дело в том, что это сложная проблема, но таблица обвязки (или таблица калибровки резервуара) — лучшая отправная точка.

Спасибо за это Бен,

Харлей

Сколько галлонов в бочке с маслом?

Стандартный баррель масла содержит 42 галлона.Это американское измерение, которое использовалось с 1800-х годов, поскольку это был объем стандартной деревянной бочки, используемой для перевозки многих типов жидкости. Для измерения объема добычи баррели нефти сгруппированы по классификациям по тысяче баррелей, одному миллиону баррелей и одному миллиарду баррелей.

Существуют и другие международные измерения, такие как 159 литров в метрической системе или 35 британских галлонов в британской системе измерения.

По мере развития нефтяной промышленности акцент просто менялся с объема на плотность, поскольку плотность является лучшим индикатором ценности.

Как вы учитываете легкую и тяжелую нефть?

Для точного измерения количества масла в барреле необходимо рассчитать плотность масла.

Плотность — это вес на единицу объема, который изменяется при изменении давления и температуры. Стандарт API для давления составляет 14,696 фунтов на квадратный дюйм и 60 градусов по Фаренгейту для температуры. Это считается базовым условием для стандартного количества масла, которое занимает один баррель нефти. Если давление выше или ниже, объем останется прежним, но масса изменится.

Показателем легкости или тяжести нефти является плотность API , которая измеряется как величина, обратная плотности относительно воды. Нефть покупается и продается в зависимости от объема и плотности API при стандартных условиях.

• Более легкие масла имеют более высокую плотность в градусах API
• Более тяжелые масла имеют меньшую плотность в градусах API

После определения плотности нефти в градусах API можно использовать формулы для расчета плотности. Расчеты используются в промышленности для повышения точности и повторяемости измерений.

Пройдите обучение по точному измерению уровня масла

Специалисты в области измерений должны иметь фундаментальное понимание того, как выполнять точные измерения масла. Ключевые компоненты включают:

• Измерение объема
• Определение температуры
• Определение плотности по API
• Определение воды
• Поверочный (масса, объем и метры)
• Расчеты

GCI предлагает учебный курс «Основы грубых измерений», чтобы помочь специалистам в области измерений понять концепции измерений, как выполнять точные вычисления и как использовать доступные инструменты в полевых условиях.3. \]

Для фиксированного \ (d, \) объем \ (V \) является функцией высоты \ (h, \), и мы хотели бы увидеть, как изменяется объем \ (V \), когда мы изменяем высоту \ (h \) ствола.

Рис. 7. Для фиксированного значения \ (d, \) объем \ (V \) является функцией высоты \ (h. \) На графике слева показано, как при фиксированном значении \ (d , \) изменения высоты \ (h \) приводят к изменениям объема \ (V. \) На рисунке справа показано, как при фиксированном значении \ (d, \) изменение высоты \ (h \) меняет радиус \ (r \) и форма цилиндрической бочки.Эта интерактивная диаграмма также присутствует в копии этой статьи «Кеплер: объем винной бочки» на сайте MatematicasVisuales. (Апплет здесь был воссоздан Лорой Тернер весной 2020 года.)

Затем Кеплер спросил: «Если \ (d \) фиксировано, какое значение \ (h \) дает наибольший объем \ (V \)?» (Теплиц, стр. 83). Произведя некоторые вычисления и сравнив их, он решил, что ответ был: \ [h = \ frac {2d} {\ sqrt {3}}. \]

Согласно Теплицу (стр. 83):

Это определило ствол определенных пропорций.Кеплер заметил, что на его родине Рейн бочки были уже и выше, чем в Австрии, где их форма была особенно близка к форме с максимальным объемом для фиксированного \ (d \) — настолько близкой, действительно, что Кеплер не мог поверить, что это так. случайно. Поэтому он вообразил, что много веков назад кто-то рассчитал форму ствола, как он сам, и научил австрийцев конструировать стволы именно таким способом — действительно очень практичным. 2, \], а несколько отклоняется от него, это мало повлияет на объем, потому что вблизи своего максимума функция изменяется очень медленно. .

То, что функция громкости изменяется очень медленно вблизи своего максимального значения, показано на графике ниже.

Рис. 8. Для фиксированного значения \ (d, \) график объема \ (V \) как функции высоты \ (h \) показывает, что вблизи максимального объема небольшие изменения высоты \ ( h \) приводят к небольшим изменениям объема \ (V. \)

Кеплер свел в таблицу значения, полученные расчетным путем, чтобы подкрепить свою идею о том, что объемы таких цилиндров с равными диагоналями очень мало изменяются в окрестности максимума (Барон, стр.116).

Рисунок 9. Таблица Кеплера объемов винных бочек различной высоты (высот) из п. 66 из его 1615 Nova Stereometria. Просмотрите эту страницу и всю книгу в Мемориальной коллекции Познера: Кеплера Новая стереометрия . (Изображение использовано с разрешения библиотек Университета Карнеги-Меллона)

А как насчет бочки вина, которую Кеплер купил для своей свадьбы в Австрии? Было ли это справедливо оценено? Согласно Теплицу (стр.83):

Таким образом, хотя австрийский метод определения цен, если его применить к рейнским баррелям, был бы явным мошенничеством, он был вполне законным для австрийских баррелей. Австрийская форма имела то преимущество, что позволяла такой быстрый и простой метод. Так что Кеплер расслабился в этом случае.

Таким образом, это был главный вклад Кеплера: он отметил, что по мере приближения к максимальному объему изменение объема для данного изменения размеров становилось меньше. Спустя несколько лет Ферма рассмотрит подобные задачи на максимум и минимум с аналогичной точки зрения.

Как рассчитать объем пруда

Как измерить объем воды в пруду
Важным предварительным условием является то, что вы должны рассчитать объем вашего пруда, поскольку это определит размер / емкость всего вашего вспомогательного оборудования для пруда, то есть фильтров, насосов, УФ-осветлителей и аэраторов.

	На диаграмме выше показан простой способ оценить объем неправильной формы, разбив его на более мелкие части.
	В этом примере пруд разделен на две основные секции A и B. Измерьте каждую секцию в футах. Все цифры следует округлить до целого фута. Для целей фильтрации лучше переоценить объем. (Это относится только к расчетам фильтрации, а НЕ к лекарствам. ХОРОШО перефильтровать, но НЕ НАДЕЖНО лечить).Объем каждой секции рассчитывается как длина x ширина x глубина. Это дает нам ответ в кубических футах. Каждый кубический фут вмещает 6¼ галлонов воды. Затем следует сложить объемы двух секций (A и B), чтобы получить общую кубатуру. Это умножается на 6,25, чтобы получить общий объем в галлонах.

* ПРИМЕЧАНИЕ: возьмите среднюю глубину, которая может включать 10 различных измерений, чтобы получить среднюю глубину пруда.

Полезный объем пруда
При выборе оборудования подходящего размера для вашего пруда; Одного фактического объема пруда недостаточно, вы должны определить эффективный объем вашего пруда, на который влияют факторы окружающей среды i.е. На ваш пруд не повлияли прямые солнечные лучи, небольшая глубина или климатические условия. В таком случае вы можете добавить к объему пруда следующее.

Если средняя глубина пруда меньше 2’6 дюймов или 75 см, добавьте 25%, так как мелкая вода нагревается сильнее и, следовательно, требует большей фильтрации.

Если пруд находится при полном солнечном свете т.е. 6 часов в сутки прибавить 25%
или частичное солнечное сияние 4–6 часов добавить 15%

ПРИМЕЧАНИЕ: в приведенной выше информации не учитываются «уровни зарыбления»

Плотность зарыбления
Необходимо сделать поправку в зависимости от вида рыбы в вашем пруду. E.грамм. Кои производят больше отходов, чем золотые рыбки, и поэтому требуют более совершенной системы фильтрации и большего внимания к деталям.

Практическое правило: рассчитайте не более 1 кг веса всей рыбы на 1000 литров воды. При минимальной глубине воды 80 см для безопасной среды обитания кои требуется глубина воды 1,5 м.

Пластиковая бочка — обзор

Решение при испытаниях на снижение давления

Некоторые параметры пласта могут быть приблизительно определены только при определенных режимах потока; поэтому важно рассчитать время, относящееся к каждому из режимов потока.Goode et al. ⁶ разработала функцию отклика на давление в горизонтальном стволе скважины для условий как депрессии, так и повышения давления. Эти уравнения реакции на давление, опубликованные в 1987 году, предполагали точку эффективного давления вдоль горизонтального ствола скважины. Более поздняя работа Кучука и др. ¹² основано на усреднении давления в условиях депрессии. Эти уравнения обеспечивают реакцию на давление во время каждого режима потока. В формуле. 3-51b q _г удобно выражать в миллиметрах кубических футов в сутки, а объемный коэффициент газового пласта, β _г , затем выражать в баррелях коллектора на миллион кубических футов в сутки, так что произведение q _г β _g находится в баррелях резервуара в день (руб / сут), как в аналогичном уравнении для слабосжимаемых жидкостей.Все свойства газа ( β _g , μ _g и C _g ) оцениваются при исходном пластовом давлении, p _i :

(3-50 a) βg = 0,1781ziTpscpiTsc

Ранний радиальный поток. Реакция ствола скважины на давление в течение этого периода потока определяется следующими уравнениями:

Случай псевдодавления:

(3-51) ψ (pi) −ψ (pwf) = 57.920 × 106qgTpsckvkyLTsc × [log (kykvtϕμgctrw2) −3.23+ 0,868 с]

Случай, квадрат давления:

(3-51 a) pi2-pwf2 = 57.920 × 106qgTμ¯gz¯psckvkyLTsc × [log (kykvtϕμgctrw2) −3,23 + 0,868s]

Случай давления:

(3-51 b) pi − pwf = 162,6qgβgμgkvkyL [log (kykvtϕμgμgkvkyL) [log (kykvtϕμ] −3.2311 +

+

)

, где s — механическое повреждение кожи в результате бурения и заканчивания. Уравнение 3-51b показывает, что график давления в стволе скважины p _wf или ( p _i — p _wf )

в зависимости от логарифма t будет иметь полукруглую прямую линию с углом наклона

(3-52) m1 = 162.6qgβgμgkvkyL

Эквивалентную проницаемость в вертикальной плоскости вокруг ствола скважины можно рассчитать как

(3-53) kvky = 162,6qgβgμgm1L

Экстраполяция полулогарифмической прямой на t = 1 час получается следующее уравнение:

(3-54) pi − p1, hr = m [log (kvkyϕμgctrw2) −323 + 0,868s]

, где p _i — начальное пластовое давление, а p _{1, hr} — давление получается при т = 1 час.Переставляя уравнение. 3-54 дает

(3-55) s = 1,151 [pi-p1, hrm1-log (kvkyϕμgctrw2 + 3,23)]

Используя уравнение. 3-55 можно оценить скин-фактор s . Если пласт является изотропным по площади ( k _x = k _y = k _h ), то с помощью уравнения. 3-52, имеем

(3-56) Lkvky = Lkeff = 162,6qgβgμgm1

, где keff (= khkv) — эффективная проницаемость коллектора. Таким образом, если известно k _eff , можно оценить длину добывающей скважины L _w . И наоборот, если длина добывающей скважины L известна по каротажу, то можно рассчитать эффективную проницаемость коллектора. Как упоминалось ранее, этот режим потока может быть непродолжительным и его трудно идентифицировать в полевых условиях.

Промежуточный линейный поток. Реакция на давление в течение этого периода потока определяется как

(3-57) pi − pwf = 0,128qgβgLhtkyϕμgct + 141,2qgμgβgLkykv (sz + s)

, где s _z — фактор псевдоскожи, вызванный частичным проникновением в вертикальное направление и задается формулой ⁹

(3-58) sz = ln (hrw) +0.25ln (kykv) −ln (sin 180 ° zwh) -1,838

, где z _w = вертикальное положение скважины, футы, и h = высота коллектора, фут. Уравнение 3-57 показывает, что график Δ p = p _i — p _wf в зависимости от t будет иметь прямую линию с наклоном

(3-59) m2 = 8,12qgβgLhμgϕctky

Следовательно, произведение длины добывающей скважины квадрат L ² и проницаемость k _y можно получить из уклона

(3-60) L2ky = (8.128qgβghm2) 2μgϕct

Кроме того, экстраполяция прямой линии на t дает

(3-61) Δp | t = 0 = 141,2qgβgμgLkykv (sz + s)

, где

(3-62) s = 0,058hkvϕμgct (pi −pwf (0 = hr) m2) −sz

Поздний радиальный поток. Реакция на давление в течение этого периода радиального (псевдорадиального) потока определяется по формуле ⁴

(3-63) pi − pwf = 162,6qgβgµgkxkyh [log (kxtϕµgctL2) −2,023] + 141,2qgµgβgLkykv (sz + s) -63 указывает на то, что график p _wf или ( p _i — p _wf ) в сравнении с log t будет показывать полулогарифмическую прямую линию с уклоном м ₃ :

(3-64) м3 = 162.6qgβgμgkxkyh

Эквивалентная горизонтальная проницаемость kxky может быть оценена как

(3-65) kh = kxky = 162,6qgβgμgm3h

Коэффициент скин-фактора также можно получить с помощью

(3-66) s = 1,151Lhkvkrm [pi − p1h −log (kxϕμgctLw2) +2.023] −sz

, где p _{1 час} получается экстраполяцией поздней полулогарифмической прямой линии радиального потока на t = 1 час. Уравнение 3-58 дает коэффициент псевдоскин. s _z также можно оценить с помощью функции Спенсера ⁶ (Рисунок 3-21):

Рисунок 3-21.Функция Спенсера (по Спенсеру, SPE Formation Evaluation , декабрь 1987 г.). ⁶

(3-67) sz = 0,07958hzrwa [ψ (ξ1) + ψ (ξ2) −ψ (ξ3) −ψ (ξ4)]

, где

ξ1 = 0,52πrwahz

ξ2 = πhz ( 2hs + 3,48rwa)

ξ3 = 3,38πrwahz

и

ξ4 = πhz (2hs = 0,52rwa)

, где

r _wa = кажущийся радиус ствола скважины, фут

h = горизонтальная скважина в центре коллектора, футы

h _z = частичное проникновение в вертикальном направлении, футы

Если нижняя и верхняя границы поддерживаются при постоянном давлении, тогда псевдорадиальный или поздний период радиального потока не будет development, ⁶ , и в последнее время будет установившийся поток.

Поздний линейный поток. Реакция на давление в течение этого периода, r , также известная как псевдостационарное состояние, определяется как ⁴

(3-68) pi − pwf = 8.128qgβg2xehμgtkyϕct + 141.2qgβgμgLkykv (sx + sz + s), где

2 x _e = ширина резервуара, футы

с _z = псевдоскинфектор из-за частичного проникновения в вертикальном направлении (уравнение 3-58 или 3-67)

с _x = коэффициент псевдоскин из-за частичного проникновения в направлении x .

Ссылка 4 дает выражение для s _x :

(3-69) sx = 0,6366hx2Lwhky / kx∑n = 1∞Ξn2n

, где

h = высота резервуара, футы

h _x = высота между колодцем и границей x , фут

Уравнение 3-68 показывает, что график p _wf ( p _i — p _wf ) в зависимости от t будет иметь прямую линию наклона м ₄ :

(3-70) m4 = 8.128qgβgμghxhϕctky

Параметр резервуара h _x или πctkyμg может быть получено как

(3-71) hx = 8.128qgβgμgm4hϕctky

или

ϕctkyμgϕ

или

ϕctkyμg ϕ = 8,128112 qgβ

2 9112

найденный скин-фактор

(3-72) s = 0,058Lhhxkvϕμgct (pi − pwf (0 = hr) m4) — (sx + sz)

, где p _wf (0 час) — давление, полученное при t = 0 час.

КАЛЬКУЛЯТОР ОБЪЕМА БАКА [Как рассчитать емкость резервуара?]

Мы понимаем, что непросто оценить, сколько галлонов или литров может вместить ваш контейнер.

Вот почему мы создали наш онлайн-калькулятор объема резервуара. 🤘

Продолжайте читать, чтобы узнать, как с помощью нашего калькулятора емкости можно легко рассчитать объем вашего резервуара.

Но сначала…

Формула калькулятора объема резервуара

Рассчитайте объем жидкости, который может вместить ваш контейнер, указав свои размеры в метрических единицах (сантиметры или метры) или британских единицах (ярды, футы или дюймы). 2 × (Заполненный \, Глубина — Frustum \, Высота) $$

Запутались? 🤔

Ниже приведены четыре полных примера, подробно показывающих, как работает наш калькулятор.

В противном случае просто введите свои размеры для вашего контейнера в наш калькулятор размера резервуара!

Примеры расчетов

✅ Цилиндрический масляный бак

• Допустим, у меня есть цилиндрический масляный резервуар, длина которого составляет 7 ярдов, а диаметр круглой поверхности составляет 5 футов (расстояние поперек круглого конца, проходящего через центральную точку).
• Я хочу рассчитать объем бака в кубических футах и ​​выяснить, сколько масла поместится в цилиндр в галлонах США.3 = 1152,1 \, США \, галл. $$

  ✅ Прямоугольный топливный бак

  • Допустим, у меня есть прямоугольный топливный бак шириной 4 фута, длиной 2 фута и высотой 10 дюймов по вертикали.
  • Я хочу рассчитать объем бака в кубических футах и ​​выяснить, сколько топлива поместится в мой бак в бочках (баррелей).
  • Я бы ввел значения в поля и выбрал правильные единицы измерения в раскрывающихся вариантах измерения.
  • Калькулятор затем выполнит следующие вычисления:

  $$ Объем = Длина × Ширина × Высота = 2 \, фут × 4 \, фут × 10 \, дюйм = 6.3 = 14,96 \, США \, галл. $$

  ✅ Горизонтальный капсульный резервуар

  • Давайте теперь представим, что у меня есть резервуар с водяной капсулой (цилиндрический резервуар с круглыми концами), который имеет диаметр 10 дюймов и длину стороны 30 дюймов по горизонтали.
  • Я хочу знать его объем в кубических дюймах и, следовательно, его вместимость по жидкости (сколько воды я могу уместить в баке) в литрах.
  • Я бы ввел значения в калькулятор, как показано на рисунке выше, выбирая правильные единицы для каждого измерения из раскрывающихся опций.3 = 3,06 \, США \, галл. $$

    ✅ Горизонтальный овальный резервуар

    • В качестве последнего примера представим, что у меня есть овальный резервуар, длина которого по горизонтали составляет 7 футов.