Формулы объема и программы для расчета объема
Содержание:
Объём геометрической фигуры — количественная характеристика пространства, занимаемого телом или веществом. В простейших случаях объём измеряется числом умещающихся в теле единичных кубов, т. е. кубов с ребром, равным единице длины. Объём тела или вместимость сосуда определяется его формой и линейными размерами.
Формула объема куба
1) Объем куба равен кубу его ребра.
V — объем куба
H — высота ребра куба
См. также: Программа для расчета объема куба.
Формула объема пирамиды
1) Объем пирамиды равен одной трети произведения площади основания S (ABCD) на высоту h (OS).
V — объем пирамиды
S — площадь основания пирамиды
h — высота пирамиды
См. также: Программа для расчета объема пирамиды.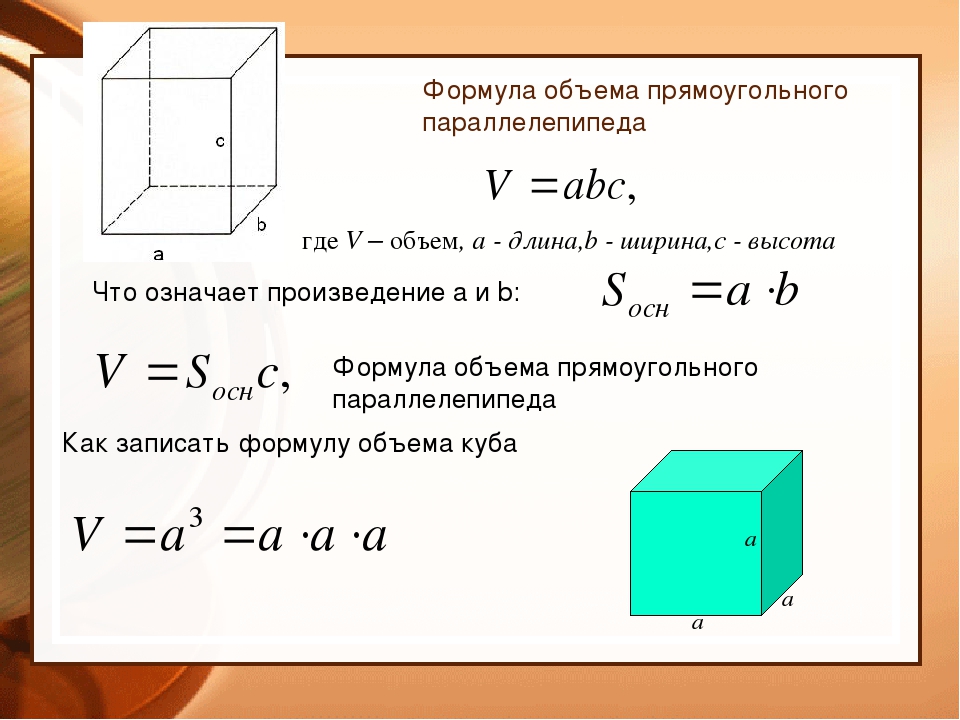
Формулы объема конуса
1) Объем конуса равен одной трети произведения площади основания на высоту.
2) Объем конуса равен одной трети произведения числа пи (3.1415) на квадрат радиуса основания на высоту.
V — объем конуса
S — площадь основания конуса
h — высота конуса
π — число пи (3.1415)
r — радиус конуса
См. также: Программа для расчета объема конуса.
Формулы объема цилиндра
1) Объем цилиндра равен произведению площади основания на высоту.
2) Объем цилиндра равен произведению числа пи (3.1415) на квадрат радиуса основания на высоту.
V — объем цилиндра
S — площадь основания цилиндра
h — высота цилиндра
π — число пи (3.1415)
r — радиус цилиндра
См. также: Программа для расчета объема цилиндра.
также: Программа для расчета объема цилиндра.
Формула объема шара
1) Объем шара вычисляется по приведенной ниже формуле.
V — объем шара
π — число пи (3.1415)
R — радиус шара
См. также: Программа для расчета объема шара.
Формула объема тетраэдра
1) Объем тетраэдра равен дроби в числителе которой корень квадратный из двух помноженный на куб длины ребра тетраэдра, а в знаменателе двенадцать.
V — объем тетраэдра
a — длина ребра тетраэдра
См. также: Программа для расчета объема тетраэдра.
Слишком сложно?
Формулы объема не по зубам? Тебе ответит эксперт через 10 минут!
Формулы объема и программы для расчета объема
Содержание:
Объём геометрической фигуры — количественная характеристика пространства, занимаемого телом или веществом.
Формула объема куба
1) Объем куба равен кубу его ребра.
V — объем куба
H — высота ребра куба
См. также: Программа для расчета объема куба.
Формула объема пирамиды
1) Объем пирамиды равен одной трети произведения площади основания S (ABCD) на высоту h (OS).
V — объем пирамиды
S — площадь основания пирамиды
h — высота пирамиды
См. также: Программа для расчета объема пирамиды.
Формулы объема конуса
1) Объем конуса равен одной трети произведения площади основания на высоту.
2) Объем конуса равен одной трети произведения числа пи (3.1415) на квадрат радиуса основания на высоту.
V — объем конуса
S — площадь основания конуса
h — высота конуса
π — число пи (3.1415)
r — радиус конуса
См. также: Программа для расчета объема конуса.
Формулы объема цилиндра
1) Объем цилиндра равен произведению площади основания на высоту.
2) Объем цилиндра равен произведению числа пи (3.1415) на квадрат радиуса основания на высоту.
V — объем цилиндра
S — площадь основания цилиндра
h — высота цилиндра
π — число пи (3.1415)
r — радиус цилиндра
См. также: Программа для расчета объема цилиндра.
Формула объема шара
1) Объем шара вычисляется по приведенной ниже формуле.
V — объем шара
π — число пи (3.
R — радиус шара
См. также: Программа для расчета объема шара.
Формула объема тетраэдра
1) Объем тетраэдра равен дроби в числителе которой корень квадратный из двух помноженный на куб длины ребра тетраэдра, а в знаменателе двенадцать.
V — объем тетраэдра
a — длина ребра тетраэдра
См. также: Программа для расчета объема тетраэдра.
Слишком сложно?
Формулы объема не по зубам? Тебе ответит эксперт через 10 минут!
Формулы объема и программы для расчета объема
Содержание:

Формула объема куба
1) Объем куба равен кубу его ребра.
V — объем куба
H — высота ребра куба
См. также: Программа для расчета объема куба.
Формула объема пирамиды
1) Объем пирамиды равен одной трети произведения площади основания S (ABCD) на высоту h (OS).
V — объем пирамиды
S — площадь основания пирамиды
h — высота пирамиды
См. также: Программа для расчета объема пирамиды.
Формулы объема конуса
1) Объем конуса равен одной трети произведения площади основания на высоту.
2) Объем конуса равен одной трети произведения числа пи (3.1415) на квадрат радиуса основания на высоту.
V — объем конуса
S — площадь основания конуса
h — высота конуса
π — число пи (3.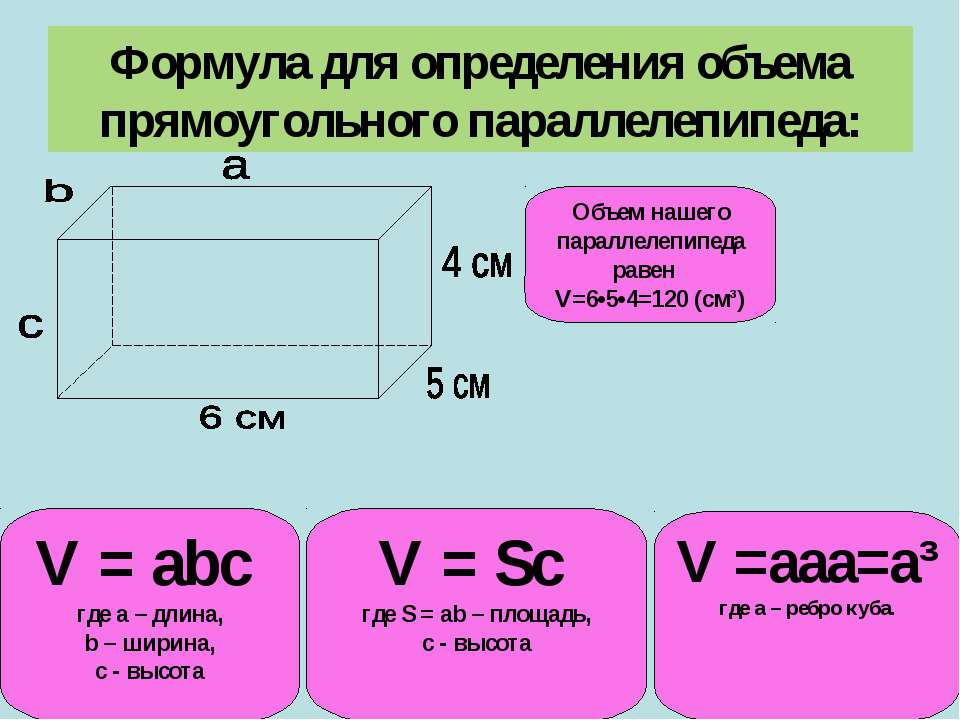
r — радиус конуса
См. также: Программа для расчета объема конуса.
Формулы объема цилиндра
1) Объем цилиндра равен произведению площади основания на высоту.
2) Объем цилиндра равен произведению числа пи (3.1415) на квадрат радиуса основания на высоту.
V — объем цилиндра
S — площадь основания цилиндра
h — высота цилиндра
π — число пи (3.1415)
r — радиус цилиндра
См. также: Программа для расчета объема цилиндра.
Формула объема шара
1) Объем шара вычисляется по приведенной ниже формуле.
V — объем шара
π — число пи (3.1415)
R — радиус шара
См. также: Программа для расчета объема шара.
Формула объема тетраэдра
1) Объем тетраэдра равен дроби в числителе которой корень квадратный из двух помноженный
на куб длины ребра тетраэдра, а в знаменателе двенадцать.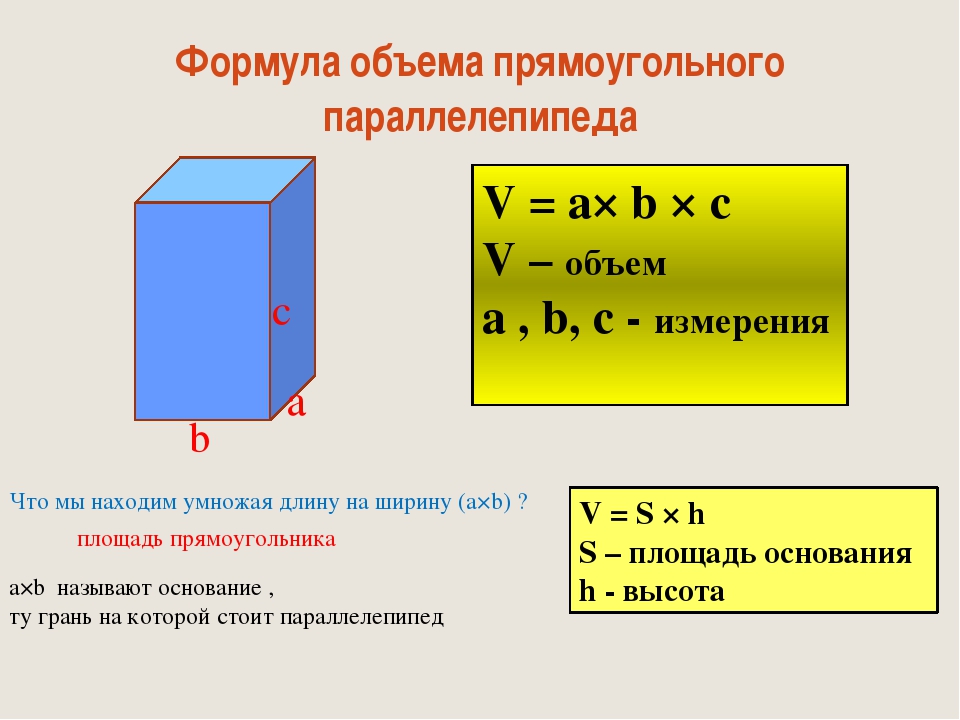
V — объем тетраэдра
a — длина ребра тетраэдра
См. также: Программа для расчета объема тетраэдра.
Слишком сложно?
Формулы объема не по зубам? Тебе ответит эксперт через 10 минут!
Расчет объема куба
Куб это геометрическое тело, ограниченное шестью квадратами, которое ещё можно назвать правильный шестигранник, а так же правильный многогранник. Слово «куб» образовано от греческого слова «kybos».
Определение объема куба
Формула расчёта объёма куба
Расчет объема куба можно произвести с помощью следующей формулы:
V = a3
a – сторона куба
V – объем куба
Куб представляет собой правильный многогранник, каждая из граней которого является квадратом. Это геометрическое тело является частным случаем других (а именно – параллелепипеда и призмы) и в повседневной жизни встречается достаточно часто.
На практике с кубами и параллелепипедами чаще всего приходится встречаться в архитектуре. Их форму имеют многие современные здания и сооружения, причем она считается одной из наиболее практичных: такие сооружения проще и быстрее как проектировать, так и возводить. При этом формула объема куба используется преимущественно для точного определения размеров внутренних пространств, что особенно важно для таких зданий, как склады, цеха промышленных предприятий, объекты социально-культурного назначения.
Форму куба нередко имеют различные предметы корпусной мебели, и при их разработке конструкторам требуется определять, в том числе, и такую величину, как объем, для того, чтобы достичь наиболее рациональной компоновки этих элементов. Вычислить объем куба часто бывает необходимо и тем инженерам, которые занимаются созданием проектов контейнеров, железнодорожных вагонов, а также стеллажных систем, использующихся в складском хозяйстве.
Одним из наиболее ярких примеров кубов является знаменитый «магический куб» – оригинальная головоломка, созданная талантливым венгерским преподавателем архитектуры и скульптором Эрне Рубиком и впоследствии названная в его честь. Каждая из граней этого кубика состоит из нескольких квадратов, окрашенных в один цвет. С помощью поворотов их можно комбинировать в различных вариантах, а задача игрока состоит в том, чтобы «разобранную» конструкцию (то есть такую, грани которой содержат квадратики разных цветов) привести в изначальное состояние. Согласно статистике, «Кубик Рубика» за все время своего существования (с 1974 года) был продан в количестве около 350 000 000 экземпляров, и на сегодняшний день является одной из признанных в мире головоломок. Изначально каждая из его граней состояла из девяти квадратов, но впоследствии появились и более сложные варианты (например, содержащие по двадцать пять элементов). В различных странах проводятся соревнования по сборке этой головоломки на время, а также чемпионаты Европы и мира, организатором которого является организация «World Cube Association» («Всемирная ассоциация кубика»).
Форму куба имеют не только рукотворные, но и некоторые природные сущности, например, кристаллические решетки такого минерала, как флюорит, а также обычной поваренной соли. Наконец, следует заметить, что с этими геометрическими телами все мы знакомы еще с детства, поскольку одними из самых любимых игрушек для многих из нас были именно кубики.
Вычисление объема цилиндра
Цилиндр это геометрическое тело, которое сформировано вращением прямоугольника на оси, совпадающей с одним из его сторон. Слово «цилиндр» происходит от греческого слова «kylindros».
Вычисление объема цилиндра
Формула расчёта объема цилиндра
Вычисление объема цилиндра производится по следующей формуле:
V = π r2h
V – объем цилиндра
h – высота цилиндра
r – радиус основания
π – 3. 14
14
Как рассчитать объем цилиндра, все мы проходили в средней школе, и этими знаниями наиболее активно пользуются в своей работе конструкторы различных машин и механизмов, потребительских товаров, а также архитекторы.
Инженерам приходится производить расчет объема цилиндра в тех случаях, когда они занимаются проектированием заданий, снабженных колоннами. Правда, в последнее время эти архитектурные элементы в их, так сказать, «классическом» варианте (то есть вместе с базой и капителем) встречаются достаточно редко, но их «упрощенные» разновидности, состоящие из одного ствола (который, собственно говоря, и представляет собой цилиндр) используются весьма широко. Нередко с колоннами приходится иметь дело реставраторам различных сооружений, имеющих большую историческую и культурную ценность, правда, в их работе вычисление объема цилиндра – далеко не самая распространенная процедура. Впрочем, если речь идет о полном восстановлении утраченных по тем или иным причинам колонн, то ее также приходится производить.
Расчет объема цилиндра осуществляется тогда, когда ведётся разработка разнообразных емкостей соответствующей формы. В качестве наглядного примера таковых можно привести, скажем, медицинские шприцы, а также колбы термосов. Следует заметить, что в первом случае такой параметр, как объем, имеет очень важное значение, поскольку от него зависит точное количество медикаментов, вводимого пациенту при инъекциях.
В технике цилиндры распространены чрезвычайно широко: достаточно сказать, что их форму имеют практически все валы и их отдельные составные части, используемые, скажем, в двигателях внутреннего сгорания. К тому же, расчет объема цилиндра – одна из важнейших задач, которую приходится решать конструкторами при проектировании современных бензиновых и дизельных силовых агрегатов, ведь от этого параметра зависит множество их характеристик, и в первую очередь такая важнейшая, как мощность. Почти все типы ДВС снабжаются поршнями, которые также имеют цилиндрическую форму.
Чрезвычайно распространенными деталями, которые присутствуют в конструкции многих сложных технических устройств, являются роликовые подшипники. Как нетрудно догадаться по самому их названию, одними из основных их компонентов являются прочные и износостойкие металлические ролики, имеющие цилиндрическую форму. Именно благодаря такой геометрии, эти детали имеют достаточно большую несущую способность и в большинстве случаев способны выдерживать весьма значительные нагрузки, чем их шариковые аналоги. Роликовые подшипники являются высокоточными деталями, и поэтому при их разработке и проектировании правильный расчет объема цилиндра (в данном случае – ролика) играет немаловажную роль.
Как рассчитать объем емкости, цилиндрического резервуара? Формула расчета.
Расчет объема цилиндрической емкости производится для вычисление полезного объема и вместимости жидкости в цилиндрической емкости или пожарного резервуара чистой воды для пожаротушения.
Вычисление основных параметров объема цилиндрической емкости (резервуара пожаротушения) выполняется на основе геометрического метода расчета объема цилиндра, в отличии от метода калибровки, где расчет объема резервуара выполняется в результате реальных замеров вместимости жидкости по данным метрштока (мерной линейки). По результатам измерений создаются таблицы калибровки резервуаров — тарировочные таблицы цистерн для определения веса жидкости, перевозимой в цистерне, по объему и удельному весу, в зависимости от уровня налива жидкости, измеренной метрштоком.
Как рассчитать объем жидкости в емкости?
Опущенный в цилиндрическую емкость до нижнего положения метршток быстро, но плавно извлекается и по линии смачивания на нем определяется высота налива жидкости в емкости в сантиметрах. По уровню жидкости в сантиметрах для каждого калибровочного типа по соответствующей таблице калибровки можно рассчитать объем жидкости в емкости в кубических дециметрах (дм.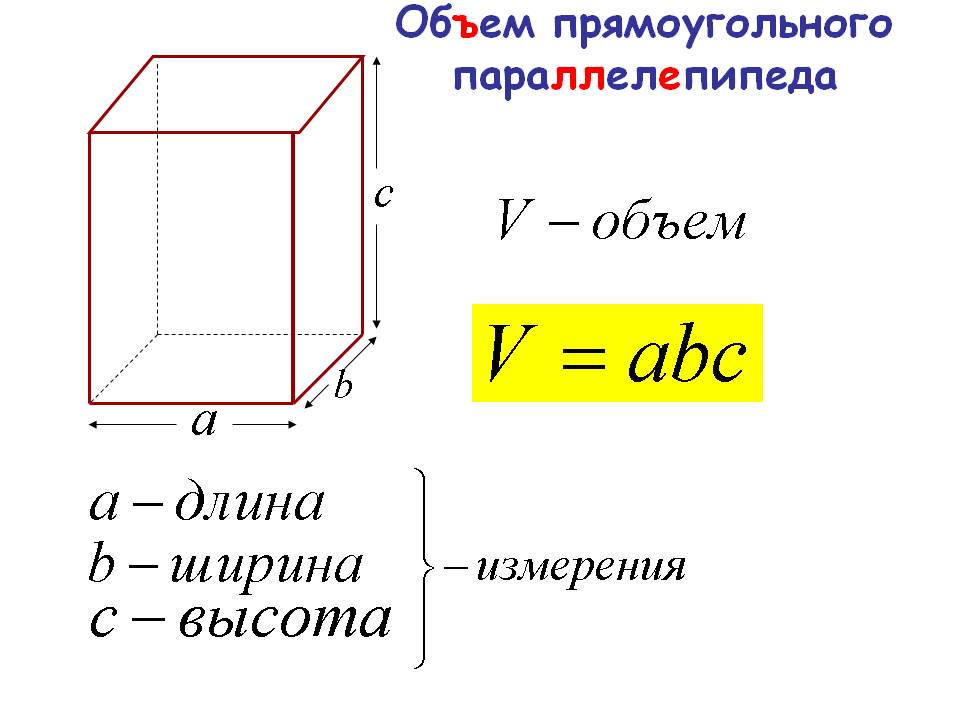 куб). От правильности замера высоты налива жидкости зависит точность определения объема жидкости в емкости, а значит, и веса груза, поэтому на тщательность замера уровня жидкости должно быть обращено самое серьезное внимание.
куб). От правильности замера высоты налива жидкости зависит точность определения объема жидкости в емкости, а значит, и веса груза, поэтому на тщательность замера уровня жидкости должно быть обращено самое серьезное внимание.
Формула расчета объема цилиндрической емкости (цилиндра)
V=S*L — расчет объема цилиндра,
где S — площадь поперечного сечения цилиндра, L — длина цилиндрической части.
Площадь поперечного сечения емкости в форме цилиндра рассчитывается по формуле:
S=3,14*d*d/4 — площадь круга с диаметром d.
Расчет объема цилиндрической емкости по формуле можно сделать как для горизонтальной, так и вертикальной накопительной емкости по их расположению. Фактически мы выполняем расчет объема цилиндра по всем известной формуле из геометрии. Расчет полезной вместимости цилиндрического резервуара можно посчитать более точно, если в формуле расчета объема горизонтальной емкости учесть толщину стенки — s.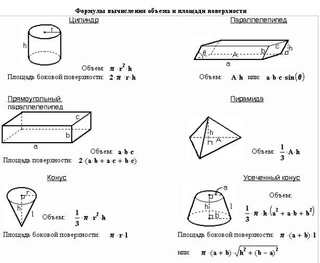 Внутренний диаметр определяют как.разность наружного диаметра и двойной толщины стенок обечайки, измеренной металлической линейкой или штангенциркулем.
Внутренний диаметр определяют как.разность наружного диаметра и двойной толщины стенок обечайки, измеренной металлической линейкой или штангенциркулем.
Длину цилиндрической части емкости определяют при помощи рулетки, измеряя расстояния между линиями пересечения днищ с цилиндрической частью резервуара. Если горизонтальный резервуар имеет плоские днища, то внутренний размер равен его наружной длине за вычетом двойной толщины днища.
Также не всегда удобно точно рассчитать диаметр емкости, для этого можно сделать измерение длины окружности, как решение, обхватить ее рулеткой. Измерить «длину окружности» гораздо легче, так как замер диаметра будет очень затруднителен в связи с тем, что сверху может находиться разного рода оборудование. К тому же можно произвести замер в трех разных сечених по объему резервуара чистой воды и сделать расчет среднего значения. Насчет «3 замеров» и «толщины стенки» — данные замеры параметров и их количество необходимо для минимизации погрешности расчета объема цилиндрической емкости, т.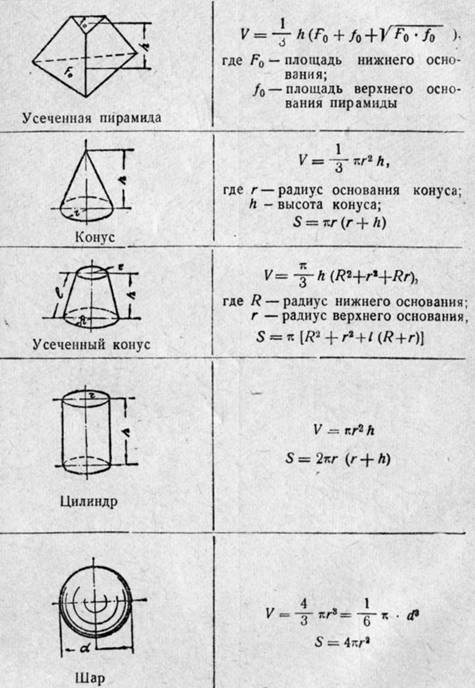 к. зачастую в процессе своей эксплуатации стенки теряют прочность, получают деформацию, уменьшаются в размерах и вместимость жидкости уменьшается.
к. зачастую в процессе своей эксплуатации стенки теряют прочность, получают деформацию, уменьшаются в размерах и вместимость жидкости уменьшается.
Длину окружности обечайки измеряют не менее двух раз в каждом сечении. Обечайка в месте измерения должна имееть чистую поверхность, а натяжение рулетки віполняют с силой 5 кГ (50 Н) — определяются с помощью пружинного динамометра. В этом случае измерение окружности может быть проведено с погрешностью ±3 мм.
Выполнить измерение длины окружности цилиндрического резервуара Lокр, и тогда можно сделать расчет диаметра цилиндра по формуле:
d=Lокр/3,14
Рассчитать объем горизонтального резервуара можно аналогично расчету объема цилиндра (см. формулу выше). Сделав расчет объема резервуара можно округлить полученное значение, и выбрать ближайшее по стандартному ряду величин объемов емкости.
Как выбрать объем емкости, резервуара?
Если Вы хотите заказать изготовление тары, то объем емкости выбираем из ряда: 50 литров, 100л, 200л, 400 литров, 500 литров, 1 м куб, 2 м3 — или выбираем литраж 2000, 3 куба, 4 куб, на выбор 5м3 -или 5000 л, 8 куб,10 м3, 1 1 куб м, 15 м3, 20 куб, 25 м3, 30 м3, 40 м3, 50 куб, 75 куб, 100 м3, емкость 1000 м3 — резервуар РВС 1000. Под заказ можно выбрать объем по вашим размерам.
Под заказ можно выбрать объем по вашим размерам.
Формула расчета объема позиции на рынке. Риск на сделку Optionclue
Качественный вход в рынок начинается с торгового плана и заканчивается расчетом объема позиции.
Если риск в каждой сделке определяется как процент от текущего капитала, то уничтожить торговый счёт не удастся при всем желании. При этом, если рынок несколько сделок подряд будет двигаться в желаемом направлении, потенциал прибыли может существенно вырасти.
Расчёт объёма позиции также важен, как и вход в правильном направлении или грамотное определение целей и точек выхода из рынка.
В этой статье я расскажу о формуле расчета объема позиции. Она незамысловата и может с лёгкостью применяться в кратко-, средне- и долгосрочной торговле. Я уверен, что её использование может сделать ваши торговые результаты более предсказуемыми и позволит стать более конкурентоспособным трейдером.
Содержание
Формула расчета объема позиции
Формула универсальна и может применяться на любых рынках. Она позволяет получить объем позиции, выраженный в контрактах. Это могут быть лоты, если речь идёт о спот–рынке (Forex) или фьючерсные контракты.
Она позволяет получить объем позиции, выраженный в контрактах. Это могут быть лоты, если речь идёт о спот–рынке (Forex) или фьючерсные контракты.
Самое главное, что на выходе будет получен объем позиции, полностью отвечающий заявленным аппетитам к риску и учитывающий в себе состояние торгового счета и рыночные реалии.
Выглядит формула следующим образом:
Рис. 1. Формула расчета объема позиции
Вы всегда можете быстро посчитать объём позиции с помощью калькулятора на главной странице нашего сайта. А сейчас давайте разберём каждый элемент формулы в отдельности.
Капитал
Капитал — объём средств, выделенных для торговли на текущем рынке с учетом рисков по открытым позициям. Другими словами, это торговый капитал за вычетом максимально возможных убытков по открытым ранее позициям.
Даже если в настоящий момент открытые позиции генерируют плавающую прибыль, но, в случае негативного развития событий, все же могут стать убыточными, учитывайте их. Это позволит в максимальной степени использовать все преимущества динамического расчета риска на сделку и защитит торговый капитал.
Это позволит в максимальной степени использовать все преимущества динамического расчета риска на сделку и защитит торговый капитал.
Риск в процентах от капитала
Риск в процентах от капитала – это риск на сделку, выраженный в процентах от капитала, выделенного для торговли на текущем рынке.
Прежде чем переходить к расчету объема позиции необходимо понять, какой долей от торгового капитала вы готовы рисковать в каждой сделке. Чаще всего, если речь идёт о консервативной торговле, риск может достигать 2% на сделку.
Рис. 2. Варианты выбора риска на сделку
Умеренная торговля подразумевает более существенные риски, например, 3-4% от капитала на трейд. Все значения риска на сделку, превышающие указанные выше, классифицируют торговлю как агрессивную.
Риск в процентах от капитала необходимо определить самостоятельно для каждого торгового счета и рынка, на котором планируется вести торги.
Если вы лишь начинаете изучать процесс торговли, я рекомендую использовать минимальные значения риска на сделку, не более 1-2% от капитала, выделенного для торговли на данном рынке.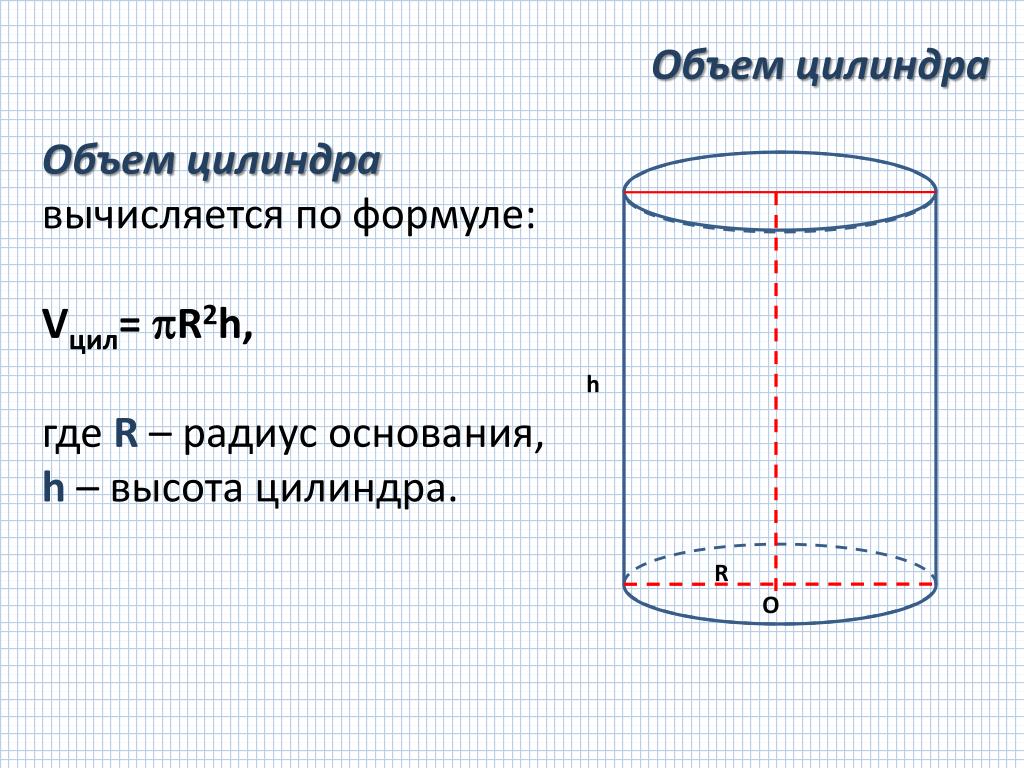
Кроме этого, новичкам не следует торговать более одной сделки в день. Это позволит упростить процесс расчёта риска на сделку, а также вынудит более скрупулёзно относиться к выбору финансового инструмента для входа в рынок.
Материалы по теме
0.01
Данное число фигурирует в числителе формулы расчёта объёма позиции лишь для того, чтобы перевести значение риска в процентах от капитала к формату, подходящему для использования в формуле.
Риск в пунктах
В знаменателе находится риск в пунктах – это расстояние между точкой входа в рынок и потенциальной точкой выхода из рынка с допустимым убытком.
Чаще всего это точка установки стоп–лосс приказа или уровень, по факту достижения которого вы планируете выйти из рынка, если цена будет двигаться в неблагоприятном направлении. Такая точка должна существовать, а риск в пунктах необходимо рассчитывать до момента входа в рынок.
Если вы рассчитываете риск на сделку после входа в рынок, то, вероятно, не знаете, чему он равен. Это недопустимо, поскольку подобное отношение к торговому счёту может привести к незапланированными и значительным убыткам.
Это недопустимо, поскольку подобное отношение к торговому счёту может привести к незапланированными и значительным убыткам.
Как рассчитать риск на сделку в пунктах
Разберем пример. Предположим, что рынок закрылся выше уровня сопротивления, вследствие чего сформировался сигнал на покупку. Возможная цена входа равна 101.00.
Рис. 3. Пример расчета потенциала риска и прибыли в пунктах при торговле на пробой уровня
Наиболее благоприятная точка для установки стоп-лосс приказа будет находиться несколько ниже ближайшего уровня поддержки текущего таймфрейма. В нашем примере стоп-лосс может быть установлен на отметке 98.89.
Расстояние между ценой входа и ценой возможного выхода из рынка с допустимым риском можно рассчитать так: 101.00 — 98.89 = 2.11.
Для того, чтобы перевести полученное значение в пункты, необходимо разделить его на размер пункта. В текущем примере, посмотрев на цену, можно увидеть два знака после запятой, следовательно, пункт равен 0. 01.
01.
Риск в пунктах равен: 2.11 / 0.01 = 211.
Обратите внимание, что вне зависимости от финансового инструмента или рынка пункт равен одной сотой (0.01) или одной десятитысячной (0.0001).
Риск в пунктах – это расстояние между ценой входа и ценой выхода в случае реализации неблагоприятного сценария. Если вы используете стоп–лосс, то риск в пунктах равен размеру стоп–лосс в пунктах.
Материалы по теме
Стоимость пункта для одного контракта
Эта переменная показывает размер прибыли или убытков, который формируется в рамках торгового счёта после покупки одного целого контракта, если рынок движется на один пункт.
Для большинства финансовых инструментов данная величина фиксирована, и ее с легкостью можно узнать на сайте брокера. Например, целый контракт на американском рынке акций зачастую равен 100 акциям, а стоимость пункта для одного контракта составляет $1.
Другими словами, при покупке одного контракта на рынке акций, движение цены на 1 пункт (на 0. 01) будет генерировать прибыль или убыток равный $1. Один доллар – стоимость пункта для одного контракта, значение, которое можно использовать в формуле.
01) будет генерировать прибыль или убыток равный $1. Один доллар – стоимость пункта для одного контракта, значение, которое можно использовать в формуле.
На рынке Forex стоимость пункта для самой популярной валютной пары EURUSD составляет $10. При покупке одного лота, объем которого составляет €100 000, движение на один пункт (0.0001) вверх будет генерировать прибыль равную $10. Таким образом, стоимость пункта для одного контракта на рынке Forex для валютной пары EURUSD будет составлять $10.
Пример расчёта объема позиции
Предположим, что капитал для торговли на финансовых рынках равен $2000. Появляется указанный выше сигнал для входа на покупку на пробой уровня на рынке валютной пары USDJPY (Рис. 3).
Позиции на данном торговом счете открываются достаточно редко, и допустимый риск от текущего капитала равен 3% на сделку.
Риск в пунктах равен 211.
Стоимость пункта для одного контракта USDJPY на момент создания статьи составляет $9.15.
Входные данные для формулы:
Объем позиции может быть рассчитан крайне просто.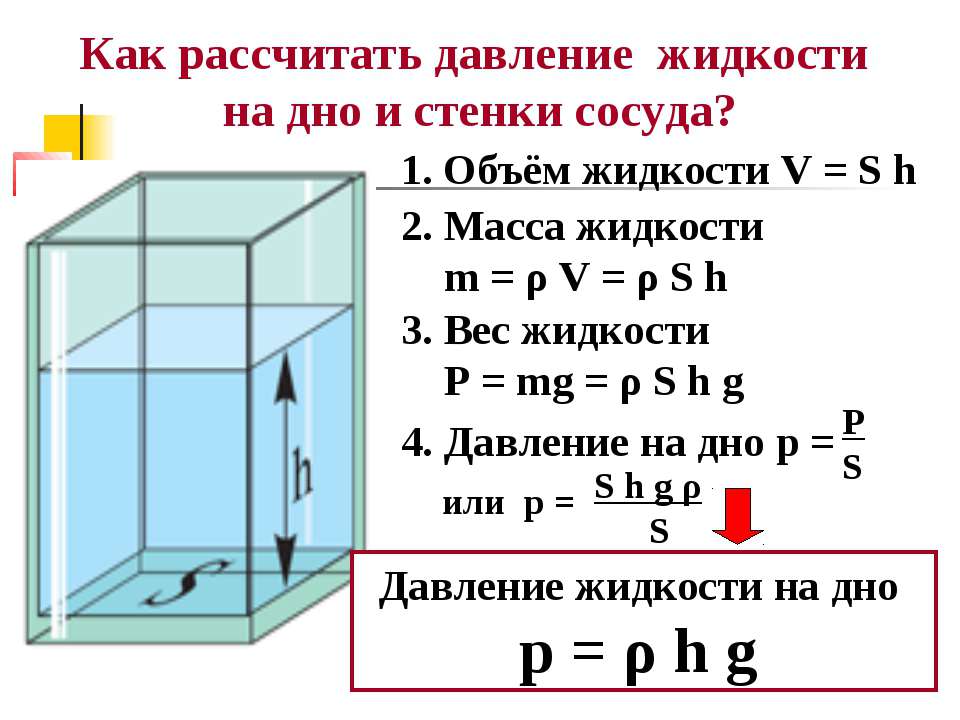 В числителе – капитал, умноженный на риск в процентах от капитала и 0.01. В знаменателе – риск в пунктах, умноженный на стоимость пункта для одного контракта:
В числителе – капитал, умноженный на риск в процентах от капитала и 0.01. В знаменателе – риск в пунктах, умноженный на стоимость пункта для одного контракта:
Объем позиции = (2000 * 3 * 0.01) / (211 * 9.15) = 60 / 1930.65 = 0.0310776
Открыть позицию именно такого объема на этом рынке нельзя, поэтому округлим полученное значение до ближайшего приемлемого — 0.03 контракта. Если допустимый риск в данной сделке составляет 3% от капитала, необходимо открыть позицию объемом 0.03 контракта.
Если сделка закроется с убытком, его размер составит: (211 * 9.15) * 0.03 = $58, что равняется 2.9% от капитала. Из-за округления объема позиции возникла погрешность, тем не менее, видно, что формула позволяет «зашить» в сделку заранее известный и допустимый уровень риска.
Материалы по теме
Точность в определении объема позиции
На рынке Forex можно торговать дробными значениями контрактов, например, купить 1.63 или 0.82 лота. Чем больше торговый капитал, тем точнее будет расчет объёма позиции, тем не менее в большинстве случаев придется округлять полученное значение.
Если ведется торговля на рынке, где подобное дробление невозможно, но требуемый для входа объем позиции менее одного целого контракта, необходимо поискать контракт меньшего размера. Например, открыть позицию несколькими мини–контрактами, мини–фьючерсами.
Рис. 4. Фьючерс Euro FX. Размер контракта на CME и MOEX
Второй вариант — поискать схожий фьючерс в других странах или на других рынках. Иногда можно найти вполне подходящий инструмент с меньшей стоимостью целого контракта (Рисунок 4).
Если найти нужный объем не удается, то, согласно торгового плана, входа в рынок нет, поскольку открыть позицию с запланированным уровнем риска на представляется возможным.
Резюме
Формула для расчета объема позиции позволяет получить оптимальное значение объема, которым можно войти в рынок. В ней учитывается текущий капитал с учетом плавающих прибылей и убытков, аппетит к риску, рыночные реалии и стоимость пункта для данного финансового инструмента.
Формула позволяет эффективно использовать каждый цент, на торговом счете реализуется эффект, подобный сложному проценту. Кривая доходности становится максимально близкой к вертикали, когда подряд закрывается ряд прибыльных сделок.
Кривая доходности становится максимально близкой к вертикали, когда подряд закрывается ряд прибыльных сделок.
Одновременно с этим снижаются риски и возможный урон торговому счету в случае получения нескольких убыточных сделок подряд. Обнуление торгового счета становится невыполнимой задачей.
Формула является универсальной и может применяться на любых рынках и таймфреймах при направленной торговле. Уверен, что ее применение сделает ваши торговые результаты еще более впечатляющими. Чтобы быстро расчитать объём сделки для вашего капитала, воспользуйтесь калькулятором на главной странице сайта OptionClue, в основе которого лежит данная формула.
Детально правила управления капиталом и рисками разбираются в рамках курса «Трейдинг. Успешный старт 2.0».
Попутного тренда!
Дополнительные материалы
Калькулятор объема
. Определение | Формулы
Измерение объема твердых тел, жидкостей и газов
Как найти объем объектов с разным состоянием материи?
- Цельный
 Если это неправильная форма, вы можете попробовать сделать то же самое, что заставило Архимеда выкрикнуть знаменитое слово * Эврика *! Вероятно, вы слышали эту историю — Архимеда попросили выяснить, сделана ли корона Иерона из чистого золота или просто позолочена, но не сгибая и не разрушая ее.Идея пришла ему в голову, когда он принимал ванну — войдя в ванну, он заметил, что уровень воды поднялся. Из этого наблюдения он пришел к выводу, что объем вытесненной воды должен быть равен объему той части его тела, которую он погрузил. Зная объем необычного объекта и его вес, он мог рассчитать плотность и сравнить ее с плотностью чистого золота. Легенда гласит, что Архимед был так взволнован этим открытием, что выскочил из ванны и побежал голым по улицам Сиракуз.
Если это неправильная форма, вы можете попробовать сделать то же самое, что заставило Архимеда выкрикнуть знаменитое слово * Эврика *! Вероятно, вы слышали эту историю — Архимеда попросили выяснить, сделана ли корона Иерона из чистого золота или просто позолочена, но не сгибая и не разрушая ее.Идея пришла ему в голову, когда он принимал ванну — войдя в ванну, он заметил, что уровень воды поднялся. Из этого наблюдения он пришел к выводу, что объем вытесненной воды должен быть равен объему той части его тела, которую он погрузил. Зная объем необычного объекта и его вес, он мог рассчитать плотность и сравнить ее с плотностью чистого золота. Легенда гласит, что Архимед был так взволнован этим открытием, что выскочил из ванны и побежал голым по улицам Сиракуз.Итак, если вы хотите измерить объем необычного объекта, просто следуйте по стопам Архимеда (хотя вы можете опустить часть «голая гонка»):
Возьмите контейнер больше, чем объект, объем которого вы хотите измерить .
 Это может быть ведро, мерный стаканчик, стакан или мерный цилиндр. На нем должна быть шкала.
Это может быть ведро, мерный стаканчик, стакан или мерный цилиндр. На нем должна быть шкала.Налейте воду в емкость и снимите показания объема.
Поместите объект внутрь .Он должен быть полностью погружен для измерения всего объема объекта. Прочтите том. Этот метод не сработает, если ваш объект растворяется в воде.
Разница между замерами — это объем нашего объекта.
Эти измерения необходимы для расчета выталкивающей силы, основанной на принципе Архимеда.
- Жидкость
Обычно измерить объем жидкости довольно просто — все, что вам нужно, это какой-нибудь мерный сосуд с градуировкой.Выберите тот, который соответствует вашим потребностям: необходимо учитывать количество жидкости и степень точности. Контейнеры, используемые для выпечки торта (посмотрите отличный калькулятор для рецепта блинов), будут отличаться от контейнеров, используемых в химии (например, при расчете молярной концентрации), будут отличаться от контейнеров, используемых в медицинских целях (например, доза лекарства).

- Газ
Для измерения объема газа необходимо использовать более сложные методы. Вы должны помнить, что на объем газа влияют температура и давление, и что газы расширяются, чтобы заполнить любой контейнер, в который они помещены. Вы можете попробовать измерить это:
Надуйте воздушный шар газом, который вы хотите измерить (например, гелием, чтобы поднять вас в воздух).Затем можно воспользоваться методом Архимеда — опустить баллон в ведро с водой и проверить разницу объемов. Здесь вы найдете подробные инструкции.
Проверьте показатели, связанные с объемом ваших легких, с помощью прибора под названием спирометр .
В химии, газовый шприц используется для ввода или отбора объема газа из закрытой системы .
 Эту лабораторную посуду также можно использовать для измерения объема газа, выделяющегося в результате химической реакции.
Эту лабораторную посуду также можно использовать для измерения объема газа, выделяющегося в результате химической реакции.
Или рассчитать :
Найдите объем газа, , учитывая его плотность и массу . Используйте простое уравнение объема
V = m / d.Рассчитайте объем сжатого газа в баллоне, используя уравнение идеального газа.
Расчет объема | SkillsYouNeed
На этой странице объясняется, как рассчитать объем твердых объектов, то есть насколько вы можете поместиться в объекте, если, например, вы заполните его жидкостью.
Площадь — это мера того, сколько места находится внутри двухмерного объекта (подробнее см. Нашу страницу: Расчет площади).
Объем — это мера пространства внутри трехмерного объекта. Наша страница, посвященная трехмерным формам, объясняет основы таких форм.
В реальном мире вычисление объема, вероятно, не то, что вы будете использовать так часто, как вычисление площади.
Однако это все еще может быть важным.Возможность рассчитать объем позволит вам, например, определить, сколько у вас места для упаковки при переезде, сколько офисного пространства вам нужно или сколько варенья вы можете уместить в банку.
Это также может быть полезно для понимания того, что имеют в виду средства массовой информации, когда они говорят о пропускной способности плотины или течении реки.
Примечание к агрегатам
Площадь выражается в квадратных единицах, потому что это два измерения, умноженные вместе.
Объем выражается в кубических единицах, потому что это сумма трех измерений (длина, ширина и глубина), умноженных вместе.Кубические единицы включают см 3 , м 3 и кубические футы.
ВНИМАНИЕ!
Объем также можно выразить как вместимость по жидкости.
Метрическая система
В метрической системе объем жидкости измеряется в литрах, что напрямую сопоставимо с кубическим размером, поскольку 1 мл = 1 см 3 . 1 литр = 1000 мл = 1000 см 3 .
1 литр = 1000 мл = 1000 см 3 .
Британская / английская система
В британской / английской системе эквивалентными измерениями являются жидкие унции, пинты, кварты и галлоны, которые нелегко перевести в кубические футы.Поэтому лучше всего придерживаться жидких или твердых единиц объема.
Подробнее см. На нашей странице Системы измерения
Основные формулы для расчета объема
Объем твердых тел на основе прямоугольников
В то время как основная формула для площади прямоугольной формы — длина × ширина, основная формула для объема — длина × ширина × высота.
То, как вы относитесь к различным размерам, не меняет расчет: вы можете, например, использовать «глубину» вместо «высоты».Важно то, что все три измерения умножаются. Вы можете умножать в любом порядке, поскольку это не изменит ответ (подробнее см. Нашу страницу о умножении ).
Коробка размером 15 см в ширину, 25 см в длину и 5 см в высоту имеет объем:
15 × 25 × 5 = 1875 см 3
Объем призм и цилиндров
Эта базовая формула может быть расширена для охвата цилиндров и призм .Вместо прямоугольного конца у вас просто другая форма: круг для цилиндров, треугольник, шестиугольник или любой другой многоугольник для призмы.
Фактически, для цилиндров и призм объем — это площадь одной стороны, умноженная на глубину или высоту формы.
Таким образом, основная формула для определения объема призм и цилиндров:
Площадь формы торца × высота / глубина призмы / цилиндра.
Объем конусов и пирамид
Тот же принцип, что и выше (ширина × длина × высота), применяется для вычисления объема конуса или пирамиды, за исключением того, что, поскольку они достигают точки, объем составляет только долю от общего количества, которое было бы, если бы они продолжались. в той же форме насквозь.
в той же форме насквозь.
Объем конуса или пирамиды составляет ровно одну треть от объема коробки или цилиндра с таким же основанием.
Следовательно, формула:
Площадь основания или торца × высота конуса / пирамиды × 1 / 3
Вернитесь на нашу страницу Расчет площади , если вы не помните, как рассчитать площадь круга или треугольника.
Например, чтобы вычислить объем конуса с радиусом 5 см и высотой 10 см:Площадь внутри круга = πr2 (где π (pi) приблизительно равно 3.14 и r — радиус круга).
В этом примере площадь основания (круга) = πr 2 = 3,14 × 5 × 5 = 78,5 см 2 .
78,5 × 10 = 785
785 × 1/3 = 261,6667 см 3
Объем сферы
Как и в случае с кругом, вам нужно π (пи), чтобы вычислить объем сферы.
Формула: 4/3 × π × радиус 3 .
Вам может быть интересно, как вычислить радиус шара.Если не протыкать через него спицу (эффективный, но конечный для мяча!), Есть более простой способ.
Вы можете измерить расстояние вокруг самой широкой точки сферы напрямую, например, с помощью рулетки. Этот круг является окружностью и имеет тот же радиус, что и сама сфера.
Длина окружности вычисляется как радиус 2 x π x.
Чтобы рассчитать радиус по окружности, вы:
Разделите окружность на (2 x π) .
Рабочие примеры: расчет объема
Пример 1
Вычислите объем цилиндра длиной 20 см, круговой конец которого имеет радиус 2,5 см.
Сначала обработайте площадь одного из круглых концов цилиндра.
Площадь круга равна πr 2 (π × радиус × радиус). π (пи) приблизительно равно 3,14.
Таким образом, площадь конца равна:
3. 14 x 2,5 x 2,5 = 19,63 см 2
14 x 2,5 x 2,5 = 19,63 см 2
Объем — это площадь конца, умноженная на длину, и поэтому составляет:
19,63 см 2 x 20 см = 392,70 см 3
Пример 2
Что больше по объему: сфера радиусом 2 см или пирамида с основанием в квадрате 2,5 см и высотой 10 см?
Сначала определим объем сферы .
Объем сферы составляет 4/3 × π × радиус 3 .
Следовательно, объем сферы:
4 ÷ 3 x 3,14 × 2 × 2 × 2 = 33,51 см 3
Затем вычислите объем пирамиды .
Объем пирамиды 1/3 × площадь основания × высота.
Площадь основания = длина × ширина = 2,5 см × 2,5 см = 6,25 см 2
Таким образом, объем составляет 1/3 x 6,25 × 10 = 20.83 см 3
Таким образом, сфера больше по объему, чем пирамида.
Расчет объема твердых частиц неправильной формы
Точно так же, как вы можете вычислить площадь неправильных двумерных форм, разбив их на правильные, вы можете сделать то же самое для вычисления объема неправильных твердых тел. Просто разделите твердое тело на более мелкие части, пока не получите только твердые тела, с которыми вы сможете легко работать.
Рабочий пример
Рассчитайте объем водяного цилиндра общей высотой 1 м, диаметром 40 см и полусферической верхней частью.
Сначала вы делите фигуру на две части: цилиндр и полусферу (полусферу).
Объем сферы составляет 4/3 × π × радиус 3 . В этом примере радиус составляет 20 см (половина диаметра). Поскольку верхняя часть является полусферической, ее объем будет вдвое меньше полной сферы. Таким образом, объем данного участка формы:
0,5 × 4/3 × π × 203 = 16,755,16 см 3
Объем цилиндра равен площади основания × высоте. Здесь высота цилиндра — это общая высота за вычетом радиуса сферы, которая составляет 1 м — 20 см = 80 см. Площадь цоколя πr 2 .
Здесь высота цилиндра — это общая высота за вычетом радиуса сферы, которая составляет 1 м — 20 см = 80 см. Площадь цоколя πr 2 .
Таким образом, объем цилиндрического сечения данной формы составляет:
80 × π × 20 × 20 = 100 530,96 см 3
Таким образом, общий объем этого резервуара для воды составляет:
100 530,96 + 16 755,16 = 117 286,12 см 3 .
Это довольно большое число, поэтому вы можете преобразовать его в 117.19 литров путем деления на 1000 (поскольку в литре 1000 см 3 ). Однако вполне правильно выразить его как cm 3 , поскольку задача не требует, чтобы ответ был выражен в какой-либо конкретной форме.
Заключение…
Используя эти принципы, если необходимо, теперь вы сможете рассчитать объем практически всего в своей жизни, будь то упаковочный ящик, комната или водяной баллон.
Как рассчитать объем
Расчет объема Объем измеряется в кубах (или кубических единицах).
Сколько кубиков в этой прямоугольной призме (кубоиде)?
Мы можем считать кубики, хотя быстрее вычислить длину, ширину и высоту и использовать умножение. Прямоугольная призма выше имеет объем 48 кубических единиц.
Объем прямоугольной призмы = длина x ширина x высота
Примеры расчета площади прямоугольникаНам нужно сделать два умножения, чтобы вычислить объем. Мы вычисляем площадь одной грани (или стороны) и умножаем ее на ее высоту.Примеры ниже показывают, как это можно сделать тремя способами.
Обратите внимание, как мы получаем один и тот же ответ независимо от того, какой стороной мы ищем область.
Когда ваш ребенок начинает работать с площадью и периметром, он или она обычно работает с двумя измерениями — квадратами, прямоугольниками, треугольниками и т. Д., Которые показаны на бумаге плоскими — нет глубины или третьего измерения. Работа с объемом действительно включает 3 измерения. Убедитесь, что ваш ребенок знает об этом и не думает о кубах и других трехмерных фигурах, показанных на бумаге, просто как о еще одной «фигуре на странице».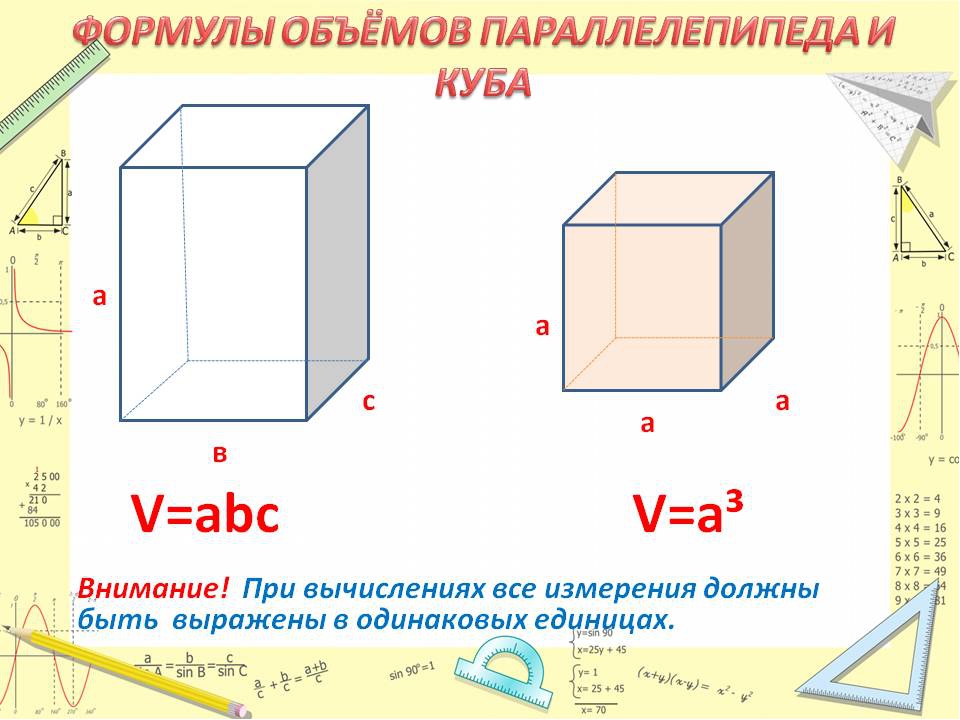 «Покажите им настоящие коробки и покажите, как их можно нарисовать (или изобразить) на двухмерном листе бумаги. Другими словами, убедитесь, что существует связь между тем, что на бумаге, и тем, что она представляет в реальном мире.
«Покажите им настоящие коробки и покажите, как их можно нарисовать (или изобразить) на двухмерном листе бумаги. Другими словами, убедитесь, что существует связь между тем, что на бумаге, и тем, что она представляет в реальном мире.
Убедитесь, что вашего ребенка не смущает использование громкости , когда речь идет о громкости.
Единицы измерения объемаЕсть очень большие различия между единицами измерения объема. Например, в 1 метре 100 сантиметров, а в кубическом метре 1000000 (да, 1 миллион) кубических сантиметров.
Почему большая разница? Потому что по объему у нас есть не только длина; у нас есть длина, ширина и высота. Пример кубика сахара ниже показывает это.
Сколько сахара? 1 м 3 или 1000000 см 3
Подумайте о наполнении очень большого ящика (шириной 1 метр, длиной 1 метр и высотой 1 метр) кубиками сахара (с каждой стороной 1 сантиметр).
| Шаг 1: один ряд вдоль дна коробки — , это будет 100 кубиков сахара | |
| Шаг 2: накройте оставшуюся часть основания коробки — , что даст в общей сложности 100 рядов с 100 кубиками сахара в каждом. 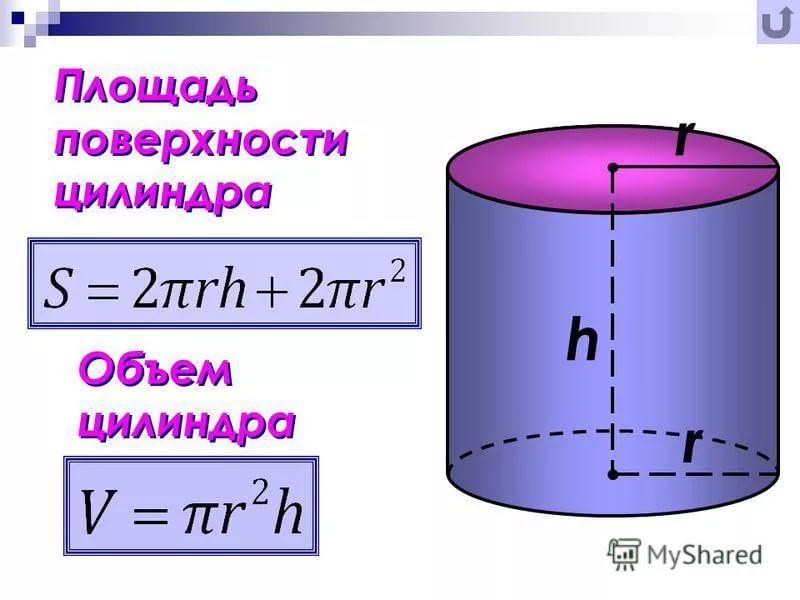 100 x 100 = 10 000 сахара. 100 x 100 = 10 000 сахара. кубиков на дне большой коробки. | |
| Шаг 3: Повторите это 99 раз, пока не получится слоев по 10 000 кубиков, уложенных стопкой в 100 слоев. 10 000 x 100 = 1 000 000 кубиков сахара |
1000000 см 3 в 1 м 3 — будьте осторожны, чтобы не было слишком много сахара!
Есть и другие единицы измерения объема; кубические дюймы, кубические футы, кубические ярды — все это единицы измерения объема.Миллилитры, литры, галлоны также используются, особенно при измерении жидкостей.
| Не забывайте крошечный 3 |
| Пишем кубические размеры с помощью маленькой 3 рядом с единицей. Мы пишем мм 3 , см 3 , м 3 , км 3 , см 3 Можно сказать «85 сантиметров в кубе» или «85 кубических сантиметров» |
| Объем = длина x ширина x высота Объем = 12 см x 8 см x 6 см = 576 см 3 | |
| Объем = длина x ширина x высота Объем = 20 м x 2 м x 2 м = 80 м 3 | |
| Объем = длина x ширина x высота Объем = 10 м x 4 м x 5 м = 200 м 3 |
Для вычисления объема цилиндра нужно умножить площадь основания на высоту цилиндра. Основание цилиндра круглое, а формула для вычисления площади круга: площадь круга = πr 2 . Здесь больше о площади круга.
Основание цилиндра круглое, а формула для вычисления площади круга: площадь круга = πr 2 . Здесь больше о площади круга.
| Объем = Площадь основания x Высота Объем = πr 2 x h Объем = πr 2 h |
Примечание: в приведенных ниже примерах мы будем использовать 3,14 как приблизительное значение для π (Pi).
Пример расчета объема цилиндра| Размеры указаны в см. | Объем = πr 2 ч Объем = 3,14 x 3 x 3 x 8 Объем = 226,08 см 3 |
Объем конуса равен одной трети объема цилиндра с соответствующей высотой и площадью основания. Это дает формулу для объема конуса, как показано ниже.
| Объем = 1/3 πr 2 ч |
| Размеры указаны в см.  | Объем = 1/3 πr 2 ч Объем = 1/3 x 3,14 x 2 x 2 x 7 Объем = 29,31 см 3 |
Формула объема шара приведена ниже.
| Объем = 4/3 πr 3 |
| Размеры указаны в см. | Объем = 4/3 πr 3 Объем = 4/3 x 3,14 x 4 x 4 x 4 Объем = 267,95 см 3 |
Используйте приведенную ниже таблицу, чтобы попрактиковаться в вычислении объемов.
Здесь вы получите другие рабочие листы геометрии по периметру, площади и т. Д.
Калькулятор длины, ширины и высоты до объема
Нажмите «Сохранить настройки», чтобы перезагрузить страницу с уникальным адресом веб-страницы для создания закладок и обмена текущими настройками инструмента.
✕ очистить настройки
Инструмент «Перевернуть» с текущими настройками и рассчитать длину, ширину или высоту
К сожалению, здесь не удалось отобразить графику, потому что ваш браузер не поддерживает холст HTML5.Сопутствующие инструменты
Руководство пользователя
Этот онлайн-инструмент вычисляет объем прямоугольной коробки, сплошного тела или пространства на основе размеров длины, ширины и высоты. Нет необходимости вводить значения в одних и тех же единицах измерения, просто выберите желаемые единицы для каждого измерения и рассчитанного объема.
После ввода размеров длины, ширины и высоты рассчитанный объем отобразится в поле ответа. Также будет показано изображение масштабированного 3D-чертежа с правильными пропорциями и помечено каждым размером и рассчитанным объемом.
Формула
Формула, используемая данным калькулятором для расчета объема объекта прямоугольной формы:
В = Д · Ш · В
Символы
- V = Объем
- L = длина
- W = Ширина
- H = высота
Объемные размеры — длина, ширина и высота
Введите длину, ширину и высоту прямоугольной формы.
Следующие коэффициенты преобразования единиц СИ в метрах (м) используются для преобразования единиц измерения, указанных для длины, ширины и высоты:
SI Метрические единицы длины префикса
- йоктометр (мкм) — 1 x 10 -24 м
- зептометр (мкм) — 1 x 10 -21 м
- аттометр (am) — 1 x 10 -18 м
- фемтометр (фм) — 1 x 10 -15 м
- пикометр (пм) — 1 x 10 -12 м
- нанометр (нм) — 1 x 10 -9 м
- микрометров (мкм) — 0.000001 м
- миллиметр (мм) — 0,001 м
- сантиметр (см) — 0,01 м
- дециметр (дм) — 0,1 м
- метр (м) — 1 м
- декаметр (плотина) — 10 м
- гектометров — 100 м
- километр (км) — 1000 м
- мегаметр (мм) — 1000000 м
- гигаметр (Gm) — 1 x 10 +9 м
- тераметр (Тм) — 1 x 10 +12 м
- петаметр (Pm) — 1 x 10 +15 м
- exametre (Em) — 1 x 10 +18 м
- зеттаметр (Zm) — 1 x 10 +21 м
- йоттаметр (Ym) — 1 x 10 +24 м
Имперские единицы и единицы длины США
- тысячных дюйма (тыс.
 ) — 0.0000254 м
) — 0.0000254 м - дюймов (дюйм) — 0,0254 м
- фут (фут) — 0,3048 м
- ярд — 0,9144 м
- миль — 1609,344 м
- морская миля (морская миля) — 1852 м
Астрономические единицы
- астрономическая единица (у.е.) — 149 597 870 700 м
- световых лет — 9,460,730,472,580,800 м
- парсек (шт) — 30 856 775 814 913 672,789… м
- килопарсек (кпк) — 3,08567758142789… x 10 +19 м
- мегапарсек (Мпк) — 3.08567758142789… x 10 +22 м
- гигапарсек (Гпк) — 3,08567758142789… x 10 +25 м
Расчет объема
Это объем прямоугольной формы, который соответствует размерам, указанным для длины, ширины и высоты. Объем рассчитывается путем умножения каждого измерения и последующего преобразования его в выбранные единицы измерения объема.
Следующие коэффициенты пересчета в кубических метрах (м³) используются для перевода вычисленного объема в различные единицы измерения объема:
Метрические единицы измерения объема
- кубический нанометр (куб нм) — 1 x 10 -27 м³
- кубических микрометров (куб мкм) — 1 x 10 -18 м³
- кубический миллиметр (куб мм) — 1 x 10 -9 м³
- кубический сантиметр (куб см) — 1 x 10 -6 м³
- миллилитр (мл) — 1 x 10 -6 м³
- чайная ложка (ч.
 Л., Метрическая) — 5 x 10 -6 м³
Л., Метрическая) — 5 x 10 -6 м³ - столовая ложка (столовая, метрическая) — 1.5 x 10 -5 м³
- стакан (метрический) — 2,5 x 10 -4 м³
- литр (л) — 1 x 10 -3 м³
- кубических метров (м3) — 1 м³
- килолитр (kL) — 1 м³
- мегалитр (ML) — 1000 м³
- кубический километр (куб км) — 1 x 10 +9 м³
Английские имперские единицы измерения объема
- тыс. Куб. (Тыс. Куб.) — 1,6387064 x 10 -14 м³
- кубических дюймов (у.е.) — 1,6387064 x 10 -5 м³
- жидких унций (жидких унций, дюймовая) — 2.84130625 x 10 -5 м³
- пинта (пинта, дюймовая) — 5,68 26125 x 10 -4 м³
- галлонов (галлоны) — 4,54609 x 10 -3 м³
- кубических футов — 0,028316846592 м³
- кубический ярд (cu yd) — 0,764554857984 м³
- кубических миль (cu mi) — 4168181825,440579584 м³
- кубических морских миль (cu nmi) — 6352182208 м³
Единицы измерения объема в США
- тыс.
 Куб. (Тыс. Куб.) — 1,6387064 x 10 -14 м³
Куб. (Тыс. Куб.) — 1,6387064 x 10 -14 м³ - чайная ложка (ч. Л., Сша) — 4.92892159375 x 10 -6 м³
- столовая ложка (Tbsp, usa) — 1.478676478125 x 10 -5 м³
- кубических дюймов (у.е.) — 1,6387064 x 10 -5 м³
- жидких унций (жидких унций, сша) — 2,95735295625 x 10 -5 м³
- стакан (США) — 2.365882365 x 10 -4 м³
- пинта (pt, жидкость сша) — 4,73176473 x 10 -4 м³
- галлонов (галлон, жидкость США) — 3,785411784 x 10 -3 м³
- кубических футов — 0.028316846592 м³
- баррель (барр., Нефть) — 0,158987294928 м³
- кубический ярд (cu yd) — 0,764554857984 м³
- кубических миль (cu mi) — 4168181825,440579584 м³
- кубических морских миль (cu nmi) — 6352182208 м³
Литры Метрическая префикс Единицы измерения объема
- йоктолитр (yL) — 1 x 10 -27 м³
- зептолитр (zL) — 1 x 10 -24 м³
- аттолитров (al) — 1 x 10 -21 м³
- фемтолитр (фл) — 1 x 10 -18 м³
- пиколитр (пл) — 1 x 10 -15 м³
- нанолитров (кв.
 нл) — 1 x 10 -12 м³
нл) — 1 x 10 -12 м³ - микролитр (кв мкл) — 1 x 10 -9 м³
- миллилитр (кв. Мл) — 0.000001 м³
- сантилитр (кв.кл) — 0,00001 м³
- децилитр (дл) — 0,0001 м³
- литр (кв. Л) — 0,001 м²
- декалитр (дал) — 0,01 м³
- гектолитр (гл) — 0,1 м³
- килолитр (кв.кл) — 1 м³
- мегалитр (ML) — 1000 м³
- гигалитр (GL) — 1000000 м³
- тералитр (TL) — 1 x 10 +9 м³
- петалитр (PL) — 1 x 10 +12 м³
- exalitre (EL) — 1 x 10 +15 м³
- цетталитр (ZL) — 1 x 10 +18 м³
- йотталитр (YL) — 1 x 10 +21 м³
Кубические метры СИ Метрическая префикс Единицы измерения объема
- кубический йоктометр (куб.м) — 1 x 10 -72 м³
- кубический зептометр (куб. Куб. М) — 1 x 10 -63 м³
- кубический аттометр (куб. М) — 1 x 10 -54 м³
- кубический фемтометр (куб фм) — 1 x 10 -45 м³
- кубический пикометр (куб.
 м.) — 1 x 10 -36 м³
м.) — 1 x 10 -36 м³ - кубический нанометр (куб.нм) — 1 x 10 -27 м³
- кубических микрометров (куб мкм) — 1 x 10 -18 м³
- кубический миллиметр (куб мм) — 1 x 10 -9 м³
- кубический сантиметр (куб см) — 0.000001 м³
- кубический дециметр (куб дм) — 0,001 м³
- кубических метров (м3) — 1 м³
- кубических декаметров (куб. Дам) — 1000 м³
- кубический гектометр (куб.м.) — 1,000,000 м³
- кубический километр (куб км) — 1 x 10 +9 м³
- кубических мегамметров (куб.мм) — 1 x 10 +18 м³
- кубический гигаметр (куб Гм) — 1 x 10 +27 м³
- кубических тераметров (куб.тм) — 1 x 10 +36 м³
- кубических петаметр (куб.м.) — 1 x 10 +45 м³
- кубический метр (куб.м.) — 1 x 10 +54 м³
- кубический зеттаметр (куб. М3) — 1 x 10 +63 м³
- кубический йоттаметр (куб.
 см) — 1 x 10 +72 м³
см) — 1 x 10 +72 м³
Кубические астрономические единицы
- кубическая астрономическая единица (у.е.) — 3.347928975810748964239359243 x 10 +33 м³
- кубических световых года (кубических световых года) — 8.4678666462371516595551248694562 x 10 +47 м³
- кубических парсек (у.е. шт) — 2,937998946096347255544756436543… x 10 +49 м³
- кубических килопарсек (у.е. кпк) — 2,937998946096347255544756436543… x 10 +58 м³
- кубических мегапарсек (куб.мпк) — 2,937998946096347255544756436543… x 10 +67 м³
- кубических гигапарсек (куб. Гигапарсек) — 2,937998946096347255544756436543… x 10 +76 м³
Приложения
Используйте этот калькулятор длины x ширины x высоты для определения объема в следующих приложениях:
- Объем отправляемой посылки для включения в отгрузочные документы
- Объем гравия, необходимый для заполнения дорожки, автостоянки или проезжей части.

- Прямоугольный резервуар для хранения.
- Вместимость грузового отсека легкового, грузового автомобиля или фургона.
- Объем загрузки автомобиля для перемещения хранилища.
- Максимальный объем резервуара для воды.
- Сколько топлива требуется для заправки бака.
- Размер связки, необходимый для предотвращения утечек и разливов из контейнеров IBC.
- Количество мешков, необходимых для каждого материала для строительного проекта.
- Количество почвы, необходимое для заполнения ящика сеялки.
- Количество воды, необходимое для наполнения аквариума / аквариума.
- Заливная емкость для пруда.
- Вместимость складского помещения из габаритов. Вместимость
- IBC.
- Объем плавательного бассейна.
- Возможное место для багажа внутри чемодана.
- Цементная смесь, необходимая для заполнения фундаментов / фундаментов.
- Объём кузова пикапа.
- Объем корпуса аудиодинамика.

- Кормушка для кормления животных.
- Объем цементной подушки садового сарая, солярия или теплицы.
Справка
Бак 25 x 10 x 12 дюймов в галлонах США
Сколько галлонов США вмещает резервуар шириной 10 дюймов, высотой 12 дюймов и длиной 25 дюймов?
Если исходить из внутренних размеров или без толщины стенок, объем резервуара составляет 12,987013 галлонов США.
Как рассчитать объем куба: формула и практика — видео и стенограмма урока
Расчет объема
Чтобы найти объем любого куба, вам необходимо знать длину, ширину и высоту.3
Результаты обучения
Когда вы закончите, вы сможете:
- Сформулировать определение куба
- Напишите формулу для расчета объема куба
- Рассчитать объем куба
Volume Calculator — вычислить объем куба, коробки, цилиндра, сферы, конуса …
Как рассчитать объем тела?
В зависимости от конкретного тела существуют разные формулы и другая необходимая информация, необходимая для расчета его объема. Ниже приведены формулы объема для наиболее распространенных типов геометрических тел — все они поддерживаются нашим онлайн-калькулятором, указанным выше. Все меры должны быть в одном блоке. Результат всегда в кубических единицах: кубические сантиметры, кубические дюймы, кубические метры, кубические футы, кубические ярды и т. Д.
Ниже приведены формулы объема для наиболее распространенных типов геометрических тел — все они поддерживаются нашим онлайн-калькулятором, указанным выше. Все меры должны быть в одном блоке. Результат всегда в кубических единицах: кубические сантиметры, кубические дюймы, кубические метры, кубические футы, кубические ярды и т. Д.
Расчет объема полезен во многих науках, при строительных работах и планировании, при транспортировке грузов, при контроле климата (например, расчет кондиционирования воздуха), управлении бассейнами и т. Д.
Объем куба
Формула объема для куба: сторона 3 , как показано на рисунке ниже:
Единственная необходимая информация — это сторона, затем вы берете ее куб и у вас есть объем куба. Это то же самое, что умножить площадь поверхности одной стороны на глубину куба. Для этого типа фигурок едва ли нужен калькулятор, чтобы делать математику.
Объем ящика
Формула объема для прямоугольной коробки: высота x ширина x длина , как показано на рисунке ниже:
Чтобы рассчитать объем ящика или прямоугольного резервуара, вам понадобятся три измерения: ширина, длина и высота.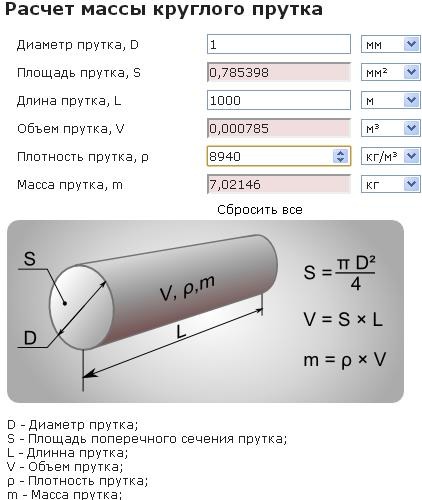 Их обычно легко измерить из-за правильности формы. Обозначая одно измерение как глубину или высоту прямоугольной призмы, умножение двух других дает нам площадь поверхности, которую затем необходимо умножить на глубину / высоту, чтобы получить объем. Чтобы рассчитать объем резервуара другой формы, воспользуйтесь нашим калькулятором объема резервуара.
Их обычно легко измерить из-за правильности формы. Обозначая одно измерение как глубину или высоту прямоугольной призмы, умножение двух других дает нам площадь поверхности, которую затем необходимо умножить на глубину / высоту, чтобы получить объем. Чтобы рассчитать объем резервуара другой формы, воспользуйтесь нашим калькулятором объема резервуара.
Объем цилиндра
Формула объема для цилиндра: высота x π x (диаметр / 2) 2 , где (диаметр / 2) — радиус основания (d = 2 xr), поэтому можно записать его другим способом: высота x π x радиус 2 .Визуализация на рисунке ниже:
Вам нужно два измерения: высота цилиндра и диаметр его основания. Во многих школьных формулах вместо этого указывается радиус, но в реальных ситуациях гораздо проще измерить диаметр, чем пытаться точно определить среднюю точку круглого основания, чтобы вы могли измерить радиус. Наш калькулятор объема требует, чтобы вы указали диаметр основания.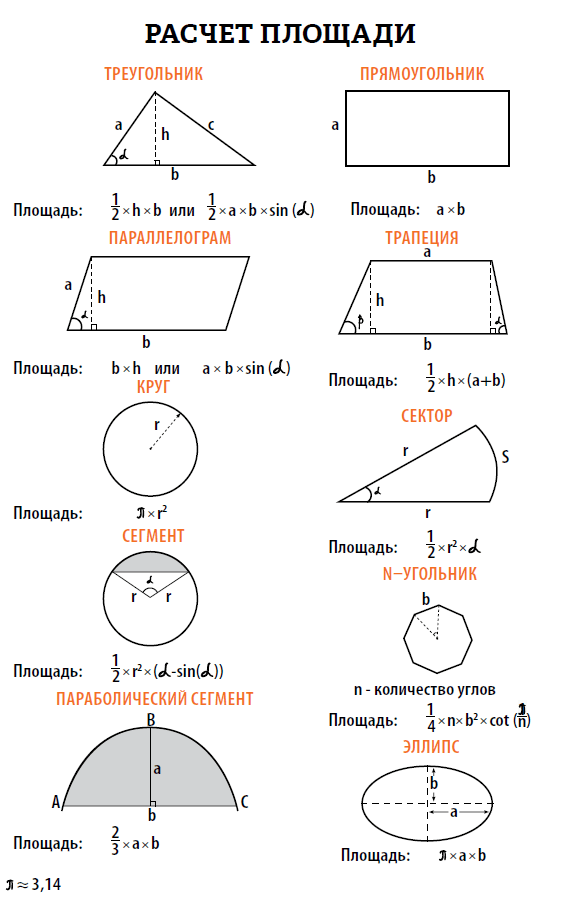 По диаметру можно рассчитать площадь поверхности основания, а затем, чтобы получить объем, просто умножьте его на высоту цилиндра.
По диаметру можно рассчитать площадь поверхности основания, а затем, чтобы получить объем, просто умножьте его на высоту цилиндра.
Объем шара
Формула объема для сферы: 4/3 x π x (диаметр / 2) 3 , где (диаметр / 2) — радиус сферы (d = 2 xr), поэтому можно записать это иначе равно 4/3 x π x радиус 3 . Наглядно на рисунке ниже:
Как и в случае с кругом, вам нужно только одно измерение сферы: ее диаметр или радиус.
Объем конуса
Формула объема для конуса: (высота x π x (диаметр / 2) 2 ) / 3 , где (диаметр / 2) — радиус основания (d = 2 xr), поэтому можно использовать другой способ напишите это (высота x π x радиус 2 ) / 3 , как показано на рисунке ниже:
Несмотря на то, что это довольно сложная форма, вам нужно знать только три измерения, чтобы вычислить объем обычного конуса.Для конусов неправильной формы, которые еще не поддерживаются нашим инструментом, вам также необходимо знать угол конуса.
Объем треугольной призмы
Формула объема для треугольной призмы: (высота x основание x длина) / 2 , как показано на рисунке ниже:
Подобно прямоугольным коробкам, вам нужно всего три измерения: высота, основание и длина.
Если вы столкнулись со строительным проектом, отделкой дома своими руками или с определенными инженерными задачами, калькулятор поможет вам, если число, которое вы хотите вычислить, попадает в любую из вышеуказанных форм.Сложные фигуры обычно можно разложить, по крайней мере приблизительно, на сумму вышеперечисленных основных фигур.
Вычислитель объема полого цилиндра
- Цель использования
- Рассчитайте вес гильзы испытательного реактора, если производитель забыл отправить ее вместе с заказом.
[1] 2021/02/06 05:09 Мужчина / Уровень 20 лет / Инженер / Очень /
- Цель использования
- Расчет массы посылки, которую мне придется нести (состоит из металлических трубок)
[2] 2020/12/05 18:54 Мужчина / До 20 лет / Старшая школа / Университет / Аспирант / Полезно /
- Цель использования
- , чтобы помочь мне прояснить сомнения в том, что было найдено совместное вычисление
[3] 2020/10/06 08:11 — / Уровень 20 лет / Начальная школа / Младший школьник / Полезно /
- Цель использования
- расчет вяжущего
[4] 2020. 06.17 17:27 Мужчина / Уровень 50 лет / Учитель / Исследователь / Полезно /
06.17 17:27 Мужчина / Уровень 50 лет / Учитель / Исследователь / Полезно /
- Цель использования
- Переуступка
- Комментарий / запрос
- Просто хотел сказать спасибо
[5] 2020/06/16 15:40 Женщина / До 20 лет / Начальная школа / Неполная средняя школа / Немного /
- Цель использования
- Используется для определения объема залитого резинового изолятора для котировки детали заказчика
- Комментарий / запрос
- Возможно, опция, которая увеличивает только десятичные разряды и не считает целые числа в уравнении
[6] 2020/05/07 22:07 Мужчина / Уровень 20 лет / Инженер / Очень /
- Цель использования
- Я, очевидно, тупой, меня сдерживали 47 лет, и это не помогает Я старый отсталый пердун, не понимающий математики
[7] 2020/03/21 02:32 — / 60 лет и старше / Начальная школа / Младшая средняя школа / Немного /
[8] 2020.


 Это может быть ведро, мерный стаканчик, стакан или мерный цилиндр. На нем должна быть шкала.
Это может быть ведро, мерный стаканчик, стакан или мерный цилиндр. На нем должна быть шкала. Эту лабораторную посуду также можно использовать для измерения объема газа, выделяющегося в результате химической реакции.
Эту лабораторную посуду также можно использовать для измерения объема газа, выделяющегося в результате химической реакции. ) — 0.0000254 м
) — 0.0000254 м Л., Метрическая) — 5 x 10 -6 м³
Л., Метрическая) — 5 x 10 -6 м³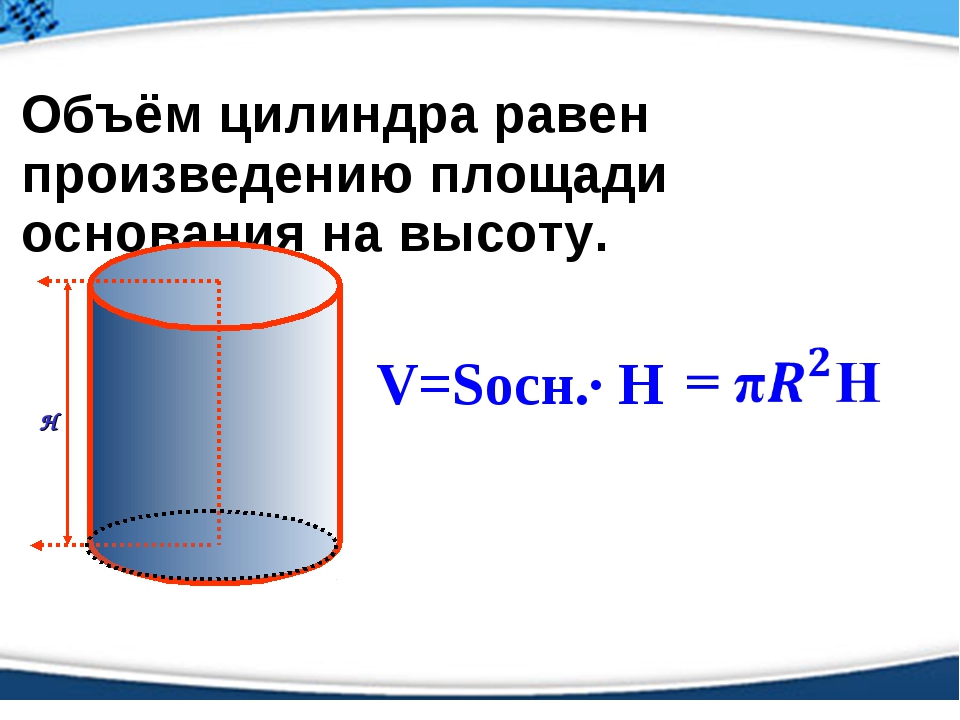 Куб. (Тыс. Куб.) — 1,6387064 x 10 -14 м³
Куб. (Тыс. Куб.) — 1,6387064 x 10 -14 м³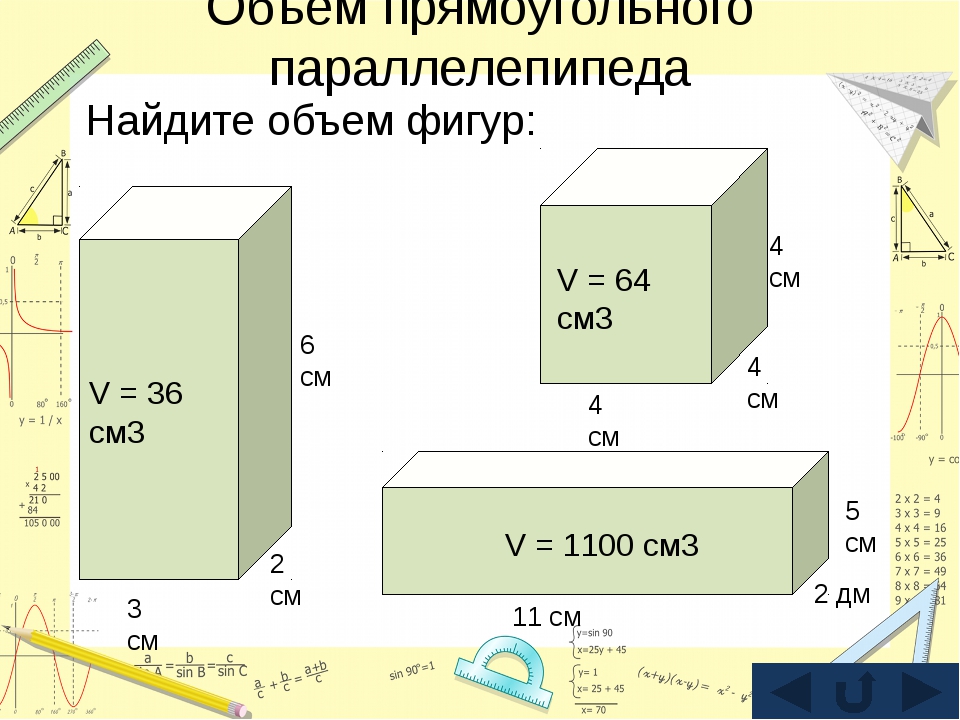 нл) — 1 x 10 -12 м³
нл) — 1 x 10 -12 м³ м.) — 1 x 10 -36 м³
м.) — 1 x 10 -36 м³ см) — 1 x 10 +72 м³
см) — 1 x 10 +72 м³
