Форма площади прямоугольника: Как найти площадь прямоугольника? Ответ на webmath.ru

Содержание

Определение площади прямоугольника

В евклидовой геометрии прямоугольником является параллелограмм, все углы которого равны 90°. Если дать более расширенное определение этой фигуры, то получится, что прямоугольником является четырехугольник, все стороны которого попарно параллельны и при этом все его углы прямые. Как вычислить площадь прямоугольника, все знают еще из школьного курса математики, в котором и дается понятие этой фигуры. В повседневной жизни ее можно встретить очень часто, можно даже сказать, что практически повсеместно.

Определение площади прямоугольника

Формула расчёта площади прямоугольника

 

S = a × b

 

a – ширина прямоугольника

b – длина прямоугольника

S – площадь прямоугольника

К примеру, форму прямоугольников имеют полы очень многих жилых, производственных и складских помещений.

Это совершенно не случайно, поскольку именно такая форма оказывается наиболее удобной и практичной при проектировании, строительстве и эксплуатации самых различных зданий. Соответственно, производить расчет площади прямоугольника очень часто приходится архитекторам, причем эти операции, ввиду простоты самой формулы, требуют затрат минимального количества времени.

Плоскости многих наиболее распространенных строительных материалов тоже представляют собой прямоугольники. К ним относятся, к примеру, кирпичи и бетонные плиты, которые изготавливаются на предприятиях промышленным способом. Следует заметить, что для обеспечения важнейших свойств некоторых стройматериалов очень важно, чтобы все углы их плоскостей были равны

90°. Это критично для обеспечения максимально плотного прилегания друг к другу пенобетонных и газобетонных блоков: только в таком случае они в полной мере демонстрируют свои отличные теплоизоляционные свойства. Кроме того, плоскости плит из минеральной ваты, широко используемые в строительстве, тоже имеют прямоугольную форму.

Такая задача, как расчет площади прямоугольника, чрезвычайно часто стоит и перед разработчиками всевозможных машин и механизмов. В них постоянно встречаются элементы именно такой формы, и для того, чтобы сконструировать какой-либо узел, требуется, чтобы они безупречно сопрягались друг с другом, поскольку в противном случае неизбежно возникновение ситуации, когда узел или агрегат будет просто невозможно собрать. На производственных предприятиях, где осуществляется изготовления машин и механизмом, в качестве сырья часто листовой металлопрокат, также имеющий

прямоугольную форму. На заготовительных и слесарных участках производится раскрой заготовок, многие из которых, прежде чем будут полностью обработаны и станут готовыми деталями, также являются прямоугольниками.

Очень многие детали корпусной мебели, которая повсеместно используется в жилых и офисных помещениях, также имеют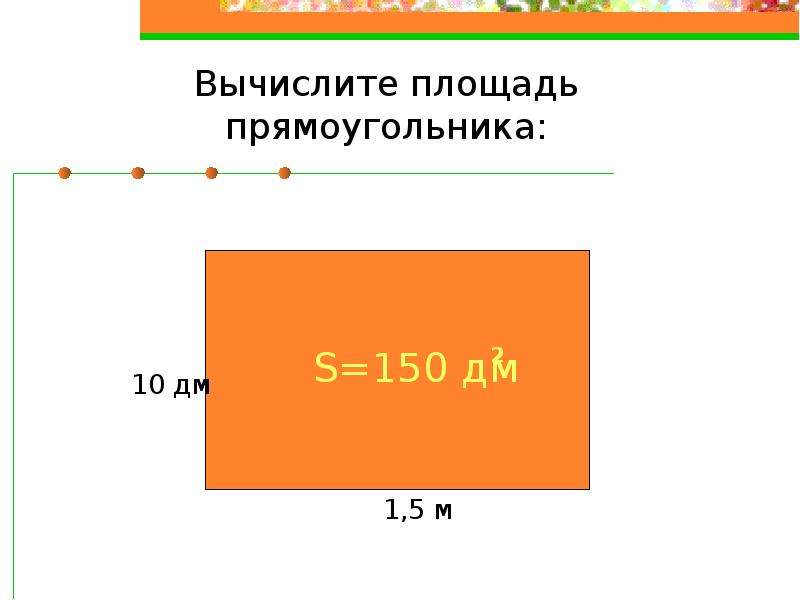

прямоугольную форму. Особенно хорошо это заметно мастерам, которые занимаются ее сборкой. Само собой разумеется, что конструкторам мебельного производства при разработке столов, шкафов, тумбочек, антресолей и т.п. также приходится постоянно сталкиваться с расчетом прямоугольников, а тем специалистам, которые занимаются непосредственно производством – изготавливать прямоугольные элементы из древесины, ДВП, ДСП, МДФ, пластика, стекла и металлов в соответствии с чертежами.

Площадь прямоугольника

Автор Ольга Андрющенко На чтение 5 мин. Просмотров 2.1k. Опубликовано

20 сентября 2020

Площадь прямоугольника очень часто требуется найти в задачах по геометрии. И не только — в повседневной жизни очень многие плоскости имеют форму прямоугольника и надо найти площадь прямоугольника. Как это сделать? Давайте рассмотрим все формулы и примеры.

Мы учимся вычислять площадь прямоугольника или площадь прямоугольника в школе. Однако, когда вы станете старше, вполне возможно, что вы не будете помнить, как найти площадь прямоугольника. Для начала давайте вспомним, что такое прямоугольник.

Что такое прямоугольник

Давайте не будем «срезать углы». Чтобы иметь возможность вычислить площадь прямоугольника, естественно, что мы сначала знаем, что это такое. Поэтому для начала необходимо помнить, что прямоугольник является четырехугольником. Другими словами, это геометрическая фигура, которая имеет четыре стороны и четыре прямых угла. Противоположные стороны прямоугольника имеют одинаковую длину. Две самые длинные стороны представляют его длину, а две другие стороны представляют его ширину.

Не все четырехугольники являются прямоугольниками. Действительно, обязательно, чтобы они имели следующие свойства, чтобы мы могли сказать, что это действительно прямоугольник:

Характеристики прямоугольника

Противоположные стороны должны быть параллельны.

  • Диагонали прямоугольника должны быть одинаковой длины. Они также пересекаются в своей середине.
  • Точка пересечения диагоналей прямоугольника называется центром симметрии.
  • Кроме того, прямоугольник также является параллелограммом, так как его стороны попарно параллельны. Однако это частный случай параллелограмма. На самом деле он имеет четыре прямых угла, и его две параллельные стороны не должны иметь одинаковую длину. В противном случае все четыре стороны имеют одинаковую длину — тогда мы говорим о квадрате.

Формула площади прямоугольника

Как рассчитать площадь прямоугольника? Обратите внимание, что базовую формулу для вычисления площади (или площади) прямоугольника очень легко запомнить. Вы просто должны умножить его длину на ширину.

Площадь прямоугольника равна его длине, умноженной на ширину.

Например, площадь прямоугольника длиной 4 сантиметра и шириной 2 сантиметра равна 4 x 2 = 8 см².

Площадь поверхности прямоугольника длиной L и шириной l равна: S = L x l

Принцип расчета площади прямоугольника

Чтобы вычислить площадь прямоугольника, мы посчитаем количество единиц областей, которые содержит прямоугольник:

В прямоугольнике выше 12 квадратов по 1 см². Его площадь составляет 12 см² (4 х 3).

Примечание. В этом расчете длина L и ширина l прямоугольника должны быть выражены в одной и той же единице длины. Результат будет выражен в той же единице измерения, возведенной в квадрат. Например, если длина прямоугольника выражена в метрах, ширина также должна быть выражена в метрах, а результат формулы для расчета площади прямоугольника даст результат в квадратных метрах (м²).

Площадь прямоугольника эквивалентна его территории. Территория — это термин, используемый для обозначения меры площади земли (мы используем единицу измерения гектар, а не м²). Гектар — это метрическая мера земельной площади, равная 10 000 м2.

Пример расчета

Рассмотрим прямоугольник длиной L = 4 см и шириной l = 2 см. Площадь S его поверхности равна:
A = L x l = 4 x 2 = 8 см².

Как рассчитать площадь прямоугольника, если мы знаем только одну сторону и диагональ

Можно определить площадь прямоугольника другим способом. Формула, которая была изложена ранее, не является единственным методом, который можно использовать. Действительно, вполне возможно сделать это по-другому. Для этого нам нужно будет, по крайней мере, измерить только одну сторону и необходимо знать длину диагонали. В этом случае мы делаем расчет, используя теорему Пифагора.

Что такое теорема Пифагора

Это формула, которая используется для определения длины третьей стороны прямоугольного треугольника, когда вы уже знаете значение двух других его сторон.

Обратите внимание, что прямоугольник состоит из двух прямоугольных треугольников. Действительно, диагональ представляет гипотенузу этого типа треугольника.

Теорема Пифагора

Кроме того, это также самая длинная сторона, которую можно найти на рисунке. Длина и ширина, с другой стороны, представляют две другие его стороны (скажем, смежные стороны). Это причина, почему можно использовать эту формулу для определения площади прямоугольника.

Теорема Пифагора основана на довольно простом уравнении, которое выглядит следующим образом: a² + b² = c².

Где a и b используются для представления двух соседних сторон — катетов прямоугольного треугольника, а c представляет гипотенузу треугольника.

Чтобы полностью понять использование этой формулы, мы начнем с очень конкретного примера. Для этого предположим, что диагональ прямоугольника 10 см, а другая сторона 6 см. Если мы ссылаемся на формулу a² + b² = c², следовательно, сторона «a» составляет 6 см, а гипотенуза «c» — 10 см. Теперь нам нужно просто заменить буквенные значения числовыми значениями, которые у нас есть. Что дает нам:

a² + b² = c²
6² + b² = 10²
b² = 10² — 6²
b² = 100 — 36
b² = 64
b= 8
Мы получаем длину смежной стороны прямоугольника «b», которая равна 8 см. Теперь мы можем рассчитать площадь прямоугольника:

S = 8 см х 6 см
Следовательно, S = 48 см².

Формулы площадей всех основных фигур

1. Формула площади равнобедренной трапеции через стороны и угол

b — верхнее основание

a — нижнее основание

c — равные боковые стороны

α — угол при нижнем основании

 

Формула площади равнобедренной трапеции через стороны, (S):

 

Формула площади равнобедренной трапеции через стороны и угол, (S):

 

 

2. Формула площади равнобокой трапеции через радиус вписанной окружности

R — радиус вписанной окружности

D — диаметр вписанной окружности

O — центр вписанной окружности

H — высота трапеции

α, β — углы трапеции

 

Формула площади равнобокой трапеции через радиус вписанной окружности, (S):

СПРАВЕДЛИВО, для вписанной окружности в равнобокую трапецию:

 

 

3. Формула площади равнобедренной трапеции через диагонали и угол между ними

d — диагональ трапеции

α, β — углы между диагоналями

 

Формула площади равнобедренной трапеции через диагонали и угол между ними, (S):

 

 

4. Формула площади равнобедренной трапеции через среднюю линию, боковую сторону и угол при основании

m — средняя линия трапеции

c — боковая сторона

α, β — углы при основании

 

Формула площади равнобедренной трапеции через среднюю линию, боковую сторону и угол при основании, (S ):

 

 

5. Формула площади равнобедренной трапеции через основания и высоту

b — верхнее основание

a — нижнее основание

h — высота трапеции

 

Формула площади равнобедренной трапеции через основания и высоту, (S):

 

Площадь сложных геометрических фигур. Как вычислить площадь фигуры. Формулы площади трапеции

Если вы планируете сделать ремонт самостоятельно, то у вас возникнет необходимость составить смету по строительным и отделочным материалам. Для этого вам понадобится рассчитать площадь помещения, в котором вы планируете произвести ремонтные работы. Главным помощником в этом выступает специально разработанная формула. Площадь помещения, а именно ее расчет, позволит вам сэкономить немалые деньги на строительных материалах и направить высвободившиеся денежные ресурсы в более нужное русло.

Геометрическая форма комнаты

Формула расчета площади помещения напрямую зависит от ее формы. Наиболее типичными для отечественных сооружений являются прямоугольные и квадратные комнаты. Однако в ходе перепланировки стандартная форма может искажаться. Комнаты бывают:

  • Прямоугольные.
  • Квадратные.
  • Сложной конфигурации (например, круглые).
  • С нишами и выступами.

Каждая из них имеет свои особенности расчета, но, как правило, используется одна и та же формула. Площадь помещения любой формы и размера, так или иначе, поддается вычислению.

Помещение прямоугольной или квадратной формы

Чтобы рассчитать площадь комнаты прямоугольной или квадратной формы, достаточно вспомнить школьные уроки геометрии. Поэтому для вас не должно составить особого труда определить площадь помещения. Формула расчета имеет вид:

S комнаты=A*B, где

А — длина помещения.

В — ширина помещения.

Для измерения этих величин вам понадобится обычная рулетка. Чтобы получить наиболее точные расчёты, стоит измерить стену с обеих сторон. Если значения не сходятся, возьмите за основу среднее значение получившихся данных. Но помните, что любые расчёты имеют свои погрешности, поэтому материал стоит закупать с запасом.

Помещение со сложной конфигурацией

Если ваша комната не попадает под определение «типичной», т.е. имеет форму круга, треугольника, многоугольника, то, возможно, для расчетов вам понадобится другая формула. Площадь помещения с такой характеристикой можно попробовать условно разделить на прямоугольные элементы и произвести расчеты стандартным путем. Если такой возможности у вас нет, тогда воспользуйтесь следующими методиками:

  • Формула нахождения площади круга:

S комн. =π*R 2 , где

R — радиус помещения.

  • Формула нахождения площади треугольника:

S комн.= √ (P(P — A) х (Р — В) х (Р — С)), где

Р — полупериметр треугольника.

А, В, С — длины его сторон.

Отсюда Р=А+В+С/2

Если в процессе расчета у вас возникли затруднения, то лучше не мучать себя и обратиться к профессионалам.

Площадь помещения с выступами и нишами

Зачастую стены украшают декоративными элементами в форме всевозможных ниш или выступов. Также их наличие может быть обусловлено необходимостью скрыть некоторые неэстетичные элементы вашей комнаты. Наличие выступов или ниш на вашей стене означает, что расчет следует проводить поэтапно. Т.е. сначала находится площадь ровного участка стены, а затем к нему прибавляется площадь ниши или выступа.

Площадь стены находится по формуле:

S стен = Р х С, где

Р — периметр

С — высота

Также нужно учитывать наличие окон и дверей. Их площадь необходимо отнять от получившегося значения.

Комната с многоуровневым потолком

Многоуровневый потолок не так сильно усложняет расчеты, как это кажется на первый взгляд. Если он имеет простую конструкцию, то можно произвести расчеты по принципу нахождения площади стен, осложненных нишами и выступами.

Однако если конструкция вашего потолка имеет дуго- и волнообразные элементы, то целесообразнее определить его площадь с помощью площади пола. Для этого необходимо:

  1. Найти размеры всех прямых участков стен.
  2. Найти площадь пола.
  3. Перемножить длину и высоту вертикальных участков.
  4. Суммировать получившееся значение с площадью пола.

Пошаговая инструкция по определению общей

площади помещения

  1. Освободите помещение от ненужных вещей. В процессе замеров вам понадобится свободный доступ ко всем участкам вашей комнаты, поэтому нужно избавиться от всего, что может этому препятствовать.
  2. Визуально разделите комнату на участки правильной и неправильной формы. Если ваше помещение имеет строго квадратную или прямоугольную форму, то этот этап можно пропустить.
  3. Сделайте произвольную схему помещения. Этот чертеж нужен для того, чтобы все данные были у вас всегда под рукой. Также он не даст вам возможности запутаться в многочисленных замерах.
  4. Замеры необходимо производить несколько раз. Это важное правило для исключения ошибок в подсчетах. Также если вы используете убедитесь, что луч лежит ровно на поверхности стены.
  5. Найдите общую площадь помещения. Формула общей площади помещения заключается в нахождении суммы всех площадей отдельных участков комнаты. Т.е. S общ.= S стен+S пола+S потолка

Соблюдение Вашей конфиденциальности важно для нас. По этой причине, мы разработали Политику Конфиденциальности, которая описывает, как мы используем и храним Вашу информацию. Пожалуйста, ознакомьтесь с нашими правилами соблюдения конфиденциальности и сообщите нам, если у вас возникнут какие-либо вопросы.

Сбор и использование персональной информации

Под персональной информацией понимаются данные, которые могут быть использованы для идентификации определенного лица либо связи с ним.

От вас может быть запрошено предоставление вашей персональной информации в любой момент, когда вы связываетесь с нами.

Ниже приведены некоторые примеры типов персональной информации, которую мы можем собирать, и как мы можем использовать такую информацию.

Какую персональную информацию мы собираем:

  • Когда вы оставляете заявку на сайте, мы можем собирать различную информацию, включая ваши имя, номер телефона, адрес электронной почты и т.д.

Как мы используем вашу персональную информацию:

  • Собираемая нами персональная информация позволяет нам связываться с вами и сообщать об уникальных предложениях, акциях и других мероприятиях и ближайших событиях.
  • Время от времени, мы можем использовать вашу персональную информацию для отправки важных уведомлений и сообщений.
  • Мы также можем использовать персональную информацию для внутренних целей, таких как проведения аудита, анализа данных и различных исследований в целях улучшения услуг предоставляемых нами и предоставления Вам рекомендаций относительно наших услуг.
  • Если вы принимаете участие в розыгрыше призов, конкурсе или сходном стимулирующем мероприятии, мы можем использовать предоставляемую вами информацию для управления такими программами.

Раскрытие информации третьим лицам

Мы не раскрываем полученную от Вас информацию третьим лицам.

Исключения:

  • В случае если необходимо — в соответствии с законом, судебным порядком, в судебном разбирательстве, и/или на основании публичных запросов или запросов от государственных органов на территории РФ — раскрыть вашу персональную информацию. Мы также можем раскрывать информацию о вас если мы определим, что такое раскрытие необходимо или уместно в целях безопасности, поддержания правопорядка, или иных общественно важных случаях.
  • В случае реорганизации, слияния или продажи мы можем передать собираемую нами персональную информацию соответствующему третьему лицу – правопреемнику.

Защита персональной информации

Мы предпринимаем меры предосторожности — включая административные, технические и физические — для защиты вашей персональной информации от утраты, кражи, и недобросовестного использования, а также от несанкционированного доступа, раскрытия, изменения и уничтожения.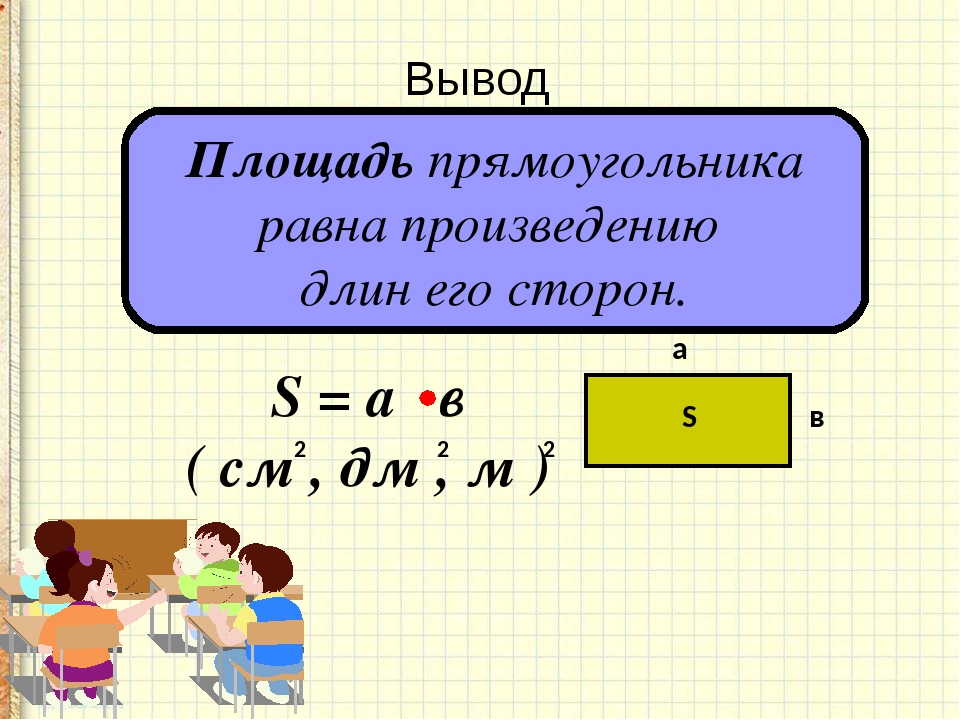

Соблюдение вашей конфиденциальности на уровне компании

Для того чтобы убедиться, что ваша персональная информация находится в безопасности, мы доводим нормы соблюдения конфиденциальности и безопасности до наших сотрудников, и строго следим за исполнением мер соблюдения конфиденциальности.

Площадь геометрической фигуры — численная характеристика геометрической фигуры показывающая размер этой фигуры (части поверхности, ограниченной замкнутым контуром данной фигуры). Величина площади выражается числом заключающихся в нее квадратных единиц.

Формулы площади треугольника

  1. Формула площади треугольника по стороне и высоте
    Площадь треугольника равна половине произведения длины стороны треугольника на длину проведенной к этой стороне высоты
  2. Формула площади треугольника по трем сторонам и радиусу описанной окружности
  3. Формула площади треугольника по трем сторонам и радиусу вписанной окружности
    Площадь треугольника равна произведения полупериметра треугольника на радиус вписанной окружности.
    4. где S — площадь треугольника,
    — длины сторон треугольника,
    — высота треугольника,
    — угол между сторонами и,
    — радиус вписанной окружности,
    R — радиус описанной окружности,

Формулы площади квадрата

  1. Формула площади квадрата по длине стороны
    Площадь квадрата равна квадрату длины его стороны.
  2. Формула площади квадрата по длине диагонали
    Площадь квадрата равна половине квадрата длины его диагонали.
    3. где S — Площадь квадрата,
    — длина стороны квадрата,
    — длина диагонали квадрата.

Формула площади прямоугольника

    Площадь прямоугольника равна произведению длин двух его смежных сторон

    где S — Площадь прямоугольника,
    — длины сторон прямоугольника.

Формулы площади параллелограмма

  1. Формула площади параллелограмма по длине стороны и высоте
    Площадь параллелограмма
  2. Формула площади параллелограмма по двум сторонам и углу между ними
    Площадь параллелограмма равна произведению длин его сторон умноженному на синус угла между ними.

    a · b · sin α

    3. где S — Площадь параллелограмма,
    — длины сторон параллелограмма,
    — длина высоты параллелограмма,
    — угол между сторонами параллелограмма.

Формулы площади ромба

  1. Формула площади ромба по длине стороны и высоте
    Площадь ромба равна произведению длины его стороны и длины опущенной на эту сторону высоты.
  2. Формула площади ромба по длине стороны и углу
    Площадь ромба равна произведению квадрата длины его стороны и синуса угла между сторонами ромба.
  3. Формула площади ромба по длинам его диагоналей
    Площадь ромба равна половине произведению длин его диагоналей.
    4. где S — Площадь ромба,
    — длина стороны ромба,
    — длина высоты ромба,
    — угол между сторонами ромба,
    1 , 2 — длины диагоналей.

Формулы площади трапеции

  1. Формула Герона для трапеции

    Где S — Площадь трапеции,
    — длины основ трапеции,
    — длины боковых сторон трапеции,

Как найти площадь фигуры?


Знать и уметь рассчитывать площади различных фигур необходимо не только для решения простых геометрических задач. Не обойтись без этих знаний и при составлении или проверке смет на ремонт помещений, расчета количества необходимых расходных материалов. Поэтому давайте разберемся, как находить площади разных фигур.

Часть плоскости, заключенная внутри замкнутого контура, называется площадью этой плоскости. Выражается площадь количеством заключенных в ней квадратных единиц.

Чтобы вычислить площадь основных геометрических фигур, необходимо использовать правильную формулу.

Площадь треугольника

Обозначения:
  1. Если известны h, a, то площадь искомого треугольника определяется как произведение длин стороны и высоты треугольника, опущенной к этой стороне, разделенное пополам: S=(a·h)/2
  2. Если известны a, b, c, то искомая площадь рассчитывается по формуле Герона: корень квадратный, взятый из произведения половины периметра треугольника и трех разностей половины периметра и каждой стороны треугольника: S = √(p·(p — a)·(p — b)·(p — c)).
  3. Если известны a, b, γ, то площадь треугольника определяется как половина произведения 2-х сторон, умноженная на значение синуса угла между этими сторонами: S=(a·b·sin γ)/2
  4. Если известны a, b, c, R, то искомая площадь определяется как деление произведения длин всех сторон треугольника на четыре радиуса описанной окружности: S=(a·b·c)/4R
  5. Если известны p, r, то искомая площадь треугольника определяется умножением половины периметра на радиус вписанной в него окружности: S=p·r

Площадь квадрата

Обозначения:
  1. Если известна сторона, то площадь данной фигуры определяется как квадрат длины его стороны: S=a 2
  2. Если известна d, то площадь квадрата определяется как половина квадрата длины его диагонали: S=d 2 /2

Площадь прямоугольника

Обозначения:
  • S — определяемая площадь,
  • a, b — длины сторон прямоугольника.
  1. Если известны a, b, то площадь данного прямоугольника определяется произведением длин двух его сторон: S=a·b
  2. Если длины сторон неизвестны, то площадь прямоугольника нужно разбить на треугольники. В этом случае площадь прямоугольника определяется как сумма площадей составляющих его треугольников.

Площадь параллелограмма

Обозначения:
  • S — искомая площадь,
  • a, b — длины сторон,
  • h — длина высоты данного параллелограмма,
  • d1, d2 — длины двух диагоналей,
  • α — угол, находящийся между сторонами,
  • γ — угол, находящийся между диагоналями.
  1. Если известны a, h, то искомая площадь определяется перемножением длин стороны и высоты, опущенной на эту сторону: S=a·h
  2. Если известны a, b, α, то площадь параллелограмма определяется перемножением длин сторон параллелограмма и значения синуса угла между этими сторонами: S=a·b·sin α
  3. Если известны d 1 , d 2 , γ то площадь параллелограмма определяется как половина произведения длин диагоналей и значения синуса угла между этими диагоналями: S=(d 1 ·d 2 ·sinγ)/2

Площадь ромба

Обозначения:
  • S — искомая площадь,
  • a — длина стороны,
  • h — длина высоты,
  • α — меньший угол между двумя сторонами,
  • d1, d2 — длины двух диагоналей.
  1. Если известны a, h, то площадь ромба определяется умножением длины стороны на длину высоты, которая опущена на эту сторону: S=a·h
  2. Если известны a, α, то площадь ромба определяется перемножением квадрата длины стороны на синус угла между сторонами: S=a 2 ·sin α
  3. Если известны d 1 и d 2 , то искомая площадь определяется как половина произведения длин диагоналей ромба: S=(d 1 ·d 2)/2

Площадь трапеции

Обозначения:
  1. Если известны a, b, c, d, то искомая площадь определяется по формуле: S= (a+b) /2 *√ .
  2. При известных a, b, h, искомая площадь определяется как произведение половины суммы оснований и высоты трапеции: S=(a+b)/2·h

Площадь выпуклого четырехугольника

Обозначения:
  1. Если известны d 1 , d 2 , α, то площадь выпуклого четырехугольника определяется как половина произведения диагоналей четырехугольника, умноженная на величину синуса угла между этими диагоналями: S=(d 1 · d 2 ·sin α)/2
  2. При известных p, r площадь выпуклого четырехугольника определяется как произведение полупериметра четырехугольника на радиус окружности, вписанной в этот четырехугольник: S=p·r
  3. Если известны a, b, c, d, θ, то площадь выпуклого четырехугольника определяется как корень квадратный из произведений разницы полупериметра и длины каждой стороны за минусом произведения длин всех сторон и квадрата косинуса половины суммы двух противоположных углов: S 2 = (p — a)(p — b)(p — c)(p — d) — abcd·cos 2 ((α+β)/2)

Площадь круга

Обозначения:

Если известен r, то искомая площадь определяется как произведение числа π на радиус в квадрате: S=π r 2

Если известна d, то площадь круга определяется как произведение числа π на квадрат диаметра, поделенное на четыре: S=(π·d 2)/4

Площадь сложной фигуры

Сложную можно разбить на простые геометрические фигуры. Площадь сложной фигуры определяется как сумма или разность составляющих площадей. Рассмотрим, к примеру, кольцо.

Обозначение:
  • S — площадь кольца,
  • R, r — радиусы внешней окружности и внутренней соответственно,
  • D, d — диаметры внешней окружности и внутренней соответственно.

Для того чтобы найти площадь кольца, надо из площади большего круга отнять площадь меньшего круга. S = S1-S2 = πR 2 -πr 2 = π (R 2 -r 2).

Таким образом, если известны R и r, то площадь кольца определяется как разница квадратов радиусов внешней и внутренней окружностей, умноженная на число пи: S=π(R 2 -r 2).

Если известны D и d, то площадь кольца определяется как четверть разницы квадратов диаметров внешней и внутренней окружностей, умноженная на число пи: S= (1/4)(D 2 -d 2) π.

Площадь закрашенной фигуры

Предположим, что внутри одного квадрата (А) находится другой (Б) (меньшего размера), и нам нужно найти закрашенную полость между фигурами «А» и «Б». Скажем так, «рамку» маленького квадрата. Для этого:

  1. Находим площадь фигуры «А» (вычисляется по формуле нахождения площади квадрата).
  2. Аналогичным образом находим площадь фигуры «Б».
  3. Вычитаем из площади «А» площадь «Б». И таким образом получаем площадь закрашенной фигуры.

Теперь вы знаете, как находить площади разных фигур.

Площади геометрических фигур — численные значения, характеризующие их размер в двумерном пространстве. Эта величина может измеряться в системных и внесистемных единицах. Так, например, внесистемная единица площади — сотка, гектар. Это в том случае, если измеряемой поверхностью является участок земли. Системная же единица площади — квадрат длины. В системе СИ принято считать, что единица площади плоской поверхности — это квадратный метр. В СГС единица площади выражается через квадратный сантиметр.

Геометрия и формулы площадей неразрывно связаны. Эта связь заключается в том, что вычисление площадей плоских фигур основывается именно на их применении. Для многих фигур выведены несколько вариантов, по которым вычисляются их квадратные размеры. Опираясь на данные из условия задачи, мы можем определить максимально простой способ для решения. Тем самым облегчить расчет и свести вероятность ошибки вычисления к минимуму. Для этого рассмотрим основные площади фигур в геометрии.

Формулы для нахождения площади любого треугольника представлены несколькими вариантами:

1) Площадь треугольника рассчитывается по основанию a и высоте h. Основанием считают сторону фигуры, на которую опущена высота. Тогда площадь треугольника:

2) Площадь прямоугольного треугольника рассчитывается точно также, если гипотенузу считать основанием. Если же за основание принять катет, то площадь прямоугольного треугольника будет равна уменьшенному вдвое произведению катетов.

На этом формулы для вычисления площади любого треугольника не заканчиваются. Другое выражение содержит стороны a,b и синусоидальную функцию угла γ, заключенного между a и b.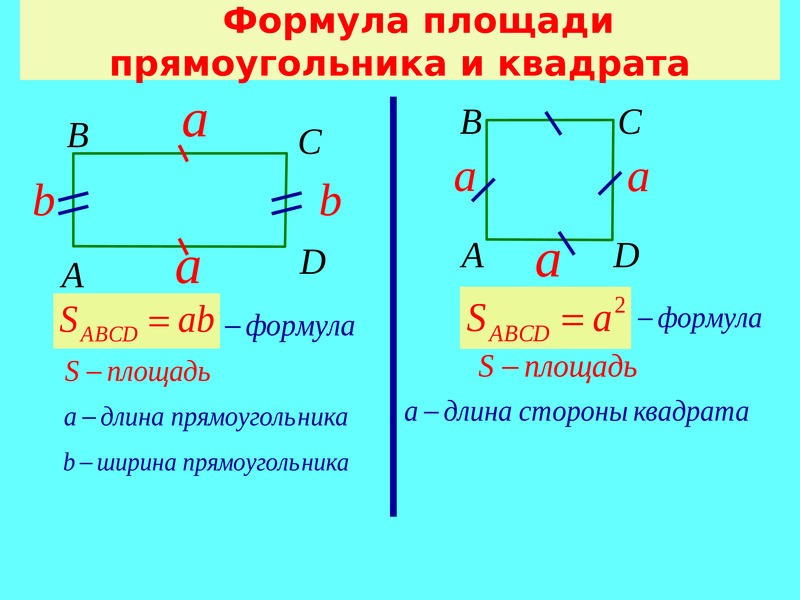 Значение синуса находится по таблицам. Также его можно узнать с помощью калькулятора. Тогда площадь треугольника:

По данному равенству тоже можно убедиться в том, что площадь прямоугольного треугольника определяется через длины катетов. Т.к. угол γ — прямой, поэтому площадь прямоугольного треугольника рассчитывается без умножения на функцию синуса.

3) Рассмотрим частный случай — правильный треугольник, у которого сторона a известна по условию или ее длина найдется при решении. О фигуре в задаче по геометрии больше ничего не известно. Тогда площадь как найти при этом условии? В этом случае применяется формула для площади правильного треугольника:

Прямоугольник

Как найти площадь прямоугольника и использовать при этом размеры сторон, имеющих общую вершину? Выражение для вычисления такое:

Если для вычисления площади прямоугольника требуется использовать длины диагоналей, то тогда понадобится функция синуса угла, образованного при их пересечении. Такая формула площади прямоугольника имеет вид:

Квадрат

Площадь квадрата определяют как вторую степень длины стороны:

Доказательство вытекает из определения, согласно которому квадратом называют прямоугольник. У всех сторон, образующих квадрат, одинаковые размеры. Поэтому вычисление площади такого прямоугольника сводится к перемножению одной на другую, т. е. ко второй степени стороны. И формула для вычисления площади квадрата примет искомый вид.

Площадь квадрата можно найти другим способом, например, если использовать диагональ:

Как вычислить площадь фигуры, которая образована частью плоскости, ограниченной окружностью? Для расчета площади формулы такие:

Параллелограмм

Для параллелограмма формула содержит линейные размеры стороны, высоты и математическое действие — умножение. Если же высота неизвестна, то тогда как найти площадь параллелограмма? Есть еще один способ вычисления. Потребуется определенное значение, которое примет тригонометрическая функция угла, образованного смежными сторонами, а также их длины.

Формулы площади параллелограмма таковы:

Ромб

Как найти площадь четырехугольника, называемого ромбом? Площадь ромба определяется с помощью простых математических действий с диагоналями. Доказательство опирается на тот факт, что отрезки диагоналей в d1 и d2 пересекаются под прямым углом. По таблице синусов видно, что для прямого угла данная функция равна единице. Поэтому площадь ромба рассчитывается так:

Еще площадь ромба может быть найдена другим способом. Доказать это тоже нетрудно, если учесть, что стороны его одинаковы по длине. Затем подставить их произведение в похожее выражение для параллелограмма. Ведь частным случаем именно этой фигуры является ромб. Здесь γ — внутренний угол ромба. Площадь ромба определяют так:

Трапеция

Как найти площадь трапеции через основания (a и b), если в задаче указаны их длины? Здесь без известного значения длины высоты h вычислить площадь такой трапеции не удастся. Т.к. эту величину содержит выражение для вычисления:

Квадратный размер прямоугольной трапеции тоже можно вычислить таким же способом. При этом учитывают, что в прямоугольной трапеции понятия высоты и боковой стороны объединены. Поэтому для прямоугольной трапеции нужно указывать вместо высоты длину боковой стороны.

Цилиндр и параллелепипед

Рассмотрим что нужно, чтобы рассчитать поверхность всего цилиндра. Площадь данной фигуры составляет пара кругов, называемых основаниями, и боковая поверхность. Окружности, образующие круги имеют длины радиусов, равные r. Для площади цилиндра имеет место такое вычисление:

Как найти площадь параллелепипеда, который состоит из трех пар граней? Его измерения совпадают с конкретной парой. Грани, находящиеся противоположно, имеют одинаковые параметры. Сначала находят S(1), S(2), S(3) — квадратные размеры неравных граней. Затем уже площадь поверхности параллелепипеда:

Кольцо

Две окружности с общим центром образуют кольцо. Они же ограничивают площадь кольца. При этом обе расчетные формулы учитывают размеры каждой окружности. Первая из них, вычисляющая площадь кольца, содержит больший R и меньший r радиусы. Чаще их называют внешним и внутренним. Во втором выражении площадь кольца рассчитывается через больший D и меньший d диаметры. Таким образом, площадь кольца по известным радиусам рассчитывают так:

Площадь кольца, с использованием длин диаметров, определяют следующим образом:

Многоугольник

Как найти площадь многоугольника, форма которого не является правильной? Общей формулы для площади таких фигур нет. Но если она изображена на координатной плоскости, например, это может быть клетчатая бумага, тогда как найти площадь поверхности в этом случае? Тут применяют способ, который не требует приблизительно измерить фигуру. Поступают так: если нашли точки, которые попадают в уголок клетки или имеют целые координаты, то учитывают только их. Чтобы затем выяснить, чему равна площадь, используют формулу, доказанную Пиком. Необходимо сложить количество точек, расположенных внутри ломаной линии с половиной точек, лежащих на ней, и вычесть единицу, т. е. вычисляется это таким образом:

где В,Г — количество точек, расположенных внутри и на всей ломаной линии соответственно.

Создание приложения Swift вычисление площади прямоугольника



Я не знаю, что делать дальше. Является ли процесс вычисления правильным? Как я могу вывести вычисление на метку?

ios swift
Поделиться Источник Chechu     29 июля 2014 в 13:20

2 ответа

  • WinForms — сколько % площади одного прямоугольника покрывает другой

    Учитывая два System.Drawing.Rectangle — х — Как определить, какой % площади первого прямоугольника покрывает второй прямоугольник? Например, если второй прямоугольник расположен на полпути к первому, то результат должен быть 50%.

  • Простой расчет площади прямоугольника сбой

    Я новичок в android и в настоящее время пытаюсь создать простое приложение, которое вычисляет площадь прямоугольника. Когда расчет выполняется, результат отображается на указанном TextView. Это мой текущий код для вычисления площади прямоугольника: package org.me.myandroidstuff; import…


0

Здесь есть несколько неправильных вещей. Вы пытаетесь назначить и Int чему-то, что ожидает строку. Вы также пытаетесь вызвать метод экземпляра вашего вычислительного класса без какого-либо экземпляра этого класса в качестве получателя. Кроме того, вы должны были бы фактически присвоить значения свойствам в указанном экземпляре, чтобы это даже сработало. Я верю, что именно это ты и собирался сделать.

class SecondViewController: UIViewController {
    @IBOutlet weak var buttonPressed: UIButton!
    @IBOutlet weak var inputLength: UITextField!
    @IBOutlet weak var inputWidth: UITextField!
    @IBOutlet weak var display: UILabel!

    override func viewDidLoad() {
        super.viewDidLoad()
    }        

    func displayComputation(sender: UIButton) {
        let computationObject = Computation()

        computationObject.inputWidth = inputWidth.text.toInt()!
        computationObject.inputLength = inputLength.text.toInt()!

        display.text = String(format: "%d", computationObject.rectanglePerimeter())
    }
}

Примечание: Ваши экземпляры должны иметь lowerCamelCase, а классы-UpperCamelCase.

Кроме того, похоже, что вы ошиблись в формуле, если хотите вычислить площадь. То, что вы делали, вычисляет периметр. Это то, чего ты хочешь.

class Computation {
    var buttonPressed = 0
    var inputLength = 0
    var inputWidth = 0

    func rectanglePerimeter() -> Int {
        return inputWidth * 2 + inputLength * 2
    }
}

Поделиться user3746217     29 июля 2014 в 13:31


0

Вы должны создать экземпляр своего класса:

class Computation {
    var inputLength = 0
    var inputWidth = 0
    func rectanglePerimeter() -> Int {
        return 2*inputLength + 2*inputWidth // I think this is what you need    
    }
}

// later
var c = Computation()
var result = c.rectanglePerimeter()

Но вам следует пересмотреть то, что вы здесь делаете — это довольно беспорядок (типы данных и их преобразование, именование классов и инкапсуляция, вычисление самого прямоугольника и т. Д.). Я думаю, что базовая книга об объектно-ориентированном программировании будет хорошей отправной точкой.

Поделиться Michael Dorner     29 июля 2014 в 13:32

Похожие вопросы:


вычисление площади прямоугольника

Я с трудом упорядочиваю свой код и хотел бы поделиться с вами своим problem, используя простой пример: вычисление площади прямоугольника. Я поставил код для примера, но чтение первого вступления в…


Вычисление площади (площадей) прямоугольника, которые не перекрываются

У меня есть два прямоугольника, представленные структурами, которые содержат координаты x1, y1, x2, y2. Один прямоугольник можно считать родительским, другой-дочерним. Я уже знаю, как определить,…


Вычисление периметра и площади прямоугольника

Мне нужно иметь возможность вводить длину и ширину прямоугольника в консоль и вычислять его периметр и площадь. У меня он работает иначе, чем принимает мои входные данные для расчетов. Я знаю, что…


WinForms — сколько % площади одного прямоугольника покрывает другой

Учитывая два System.Drawing.Rectangle — х — Как определить, какой % площади первого прямоугольника покрывает второй прямоугольник? Например, если второй прямоугольник расположен на полпути к…


Простой расчет площади прямоугольника сбой

Я новичок в android и в настоящее время пытаюсь создать простое приложение, которое вычисляет площадь прямоугольника. Когда расчет выполняется, результат отображается на указанном TextView. Это мой…


Простая функция площади прямоугольника Javascript

Я пишу простую функцию для вычисления площади прямоугольника… Вот мой код: <form id=rectangleForm method=post> <h2>Calculate the area of a rectangle:</h2> <div> <label…


Вычисление площади окружности в Java

Мне нужно написать программу для вычисления площади круга, и у меня, кажется, все в порядке, за исключением того, что когда я запускаю программу и вводю значения, вычисление площади получается…


Вычисление площади, длины и ширины прямоугольника-Java

Я знаю, что была такая же нить: Вычисление периметра и площади прямоугольника но я все еще не знаю, что делать. public class Rectangle { double length, height, rectArea; // assigning variables for…


C Программирование вычисление площади прямоугольника

Я пишу программу для вычисления площади прямоугольника. Напр.. Введите верхнюю левую точку: 1 1 (ввод пользователя) Введите нижнюю правую точку: 2 -1 (ввод пользователя) Вверху слева x = 1.000000 y:…


Python вычисление площади прямоугольника для элементов списка

У меня есть такой список, и я хочу вычислить площадь прямоугольника для элементов этого списка. list = [(3,4),(10,3),(5,6),(1,9)] выход = 12, 30, 30, 9 Я попробовал этот код, но результат-…

3 класс, периметр и площадь прямоугольника

Дата публикации: .

Что такое прямоугольник и квадрат

Прямоугольник – это четырёхугольник, у которого все углы прямые. Значит, противоположные стороны равны друг другу.

Квадрат – это прямоугольник, у которого равны и стороны, и углы. Его называют правильным четырёхугольником.


Четырёхугольники, в том числе прямоугольники и квадраты, обозначаются 4 буквами – вершинами. Для обозначения вершин используют латинские буквы: A, B, C, D …

Пример.
Читается так: четырёхугольник ABCD; квадрат EFGH.

Что такое периметр прямоугольника? Формула расчета периметра


Периметр прямоугольника – это сумма длин всех сторон прямоугольника или сумма длины и ширины, умноженная на 2.

Периметр обозначается латинской буквой P. Так как периметр – это длина всех сторон прямоугольника, то он периметр записывается в единицах длины: мм, см, м, дм, км.

Например, периметр прямоугольника АВСD обозначается как PABCD, где А, В, С, D – это вершины прямоугольника.

Запишем формулу периметра четырехугольника ABCD:

PABCD = AB + BC + CD + AD = 2 * AB + 2 * BC = 2 * (AB + BC)


Пример.
Задан прямоугольник ABCD со сторонами: AB=СD=5 см и AD=BC=3 см.
Определим PABCD.

Решение:
1. Нарисуем прямоугольник ABCD с исходными данными.
2. Напишем формулу для расчета периметра данного прямоугольника:

PABCD = 2 * (AB + BС)


3. Подставим в формулу наши данные:

PABCD = 2 * (5 см + 3 см) = 2 * 8 см = 16 см


Ответ: PABCD = 16 см.

Формула расчета периметра квадрата


У нас есть формула для определения периметра прямоугольника.

PABCD = 2 * (AB + BC)


Применим её для определения периметра квадрата. Учитывая, что все стороны квадрата равны, получаем:

PABCD= 4 * AB


Пример.
Задан квадрат ABCD со стороной, равной 6 см. Определим периметр квадрата.

Решение.
1. Нарисуем квадрат ABCD с исходными данными.

2. Вспомним формулу расчета периметра квадрата:

PABCD = 4 * AB


3. Подставим в формулу наши данные:

PABCD = 4 * 6 см = 24 см

Ответ: PABCD = 24 см.

Задачи на нахождение периметра прямоугольника

1. Измерь ширину и длину прямоугольников. Определи их периметр.

2. Нарисуй прямоугольник ABCD со сторонами 4 см и 6 см. Определи периметр прямоугольника.

3. Нарисуй квадрат СEOM со стороной 5 см. Определи периметр квадрата.

Где используется расчет периметра прямоугольника?


1. Задан участок земли, его нужно обнести забором. Какой длины будет забор?


В данной задаче необходимо точно рассчитать периметр участка, чтобы не купить лишний материал для постройки забора.

2. Родители решили сделать ремонт в детской комнате. Необходимо знать периметр комнаты и её площадь, чтобы правильно рассчитать количество обоев.
Определи длину и ширину комнаты, в которой ты живешь. Определи периметр своей комнаты.

Что такое площадь прямоугольника?


Площадь – это числовая характеристика фигуры. Площадь измеряется квадратными единицами длины: см2, м2, дм2 и др. (сантиметр в квадрате, метр в квадрате, дециметр в квадрате и т.д.)
В вычислениях обозначается латинской буквой S.

Для определения площади прямоугольника необходимо длину прямоугольника умножить на его ширину.
Площадь прямоугольника вычисляется умножением длины АК на ширину КМ. Запишем это в виде формулы.

S AKMO = AK * KM


Пример.
Чему равна площадь прямоугольника AKMO, если его стороны равны 7 см и 2 см?

S AKMO= AK * KM = 7 см * 2 см = 14 см2.

Ответ: 14 см2.

Формула вычисления площади квадрата


Площадь квадрата можно определить, умножив сторону саму на себя.

Пример.
В данном примере площадь квадрата вычисляется умножением стороны АB на ширину BC, но так как они равны, получается умножение стороны AB на AB.

S AВСО = AB * BC = AB * AB


Пример.
Определи площадь квадрата AKMO со стороной 8 см.

S AKMО = AK * KM = 8 см * 8 см = 64 см2

Ответ: 64 см2.

Задачи на нахождение площади прямоугольника и квадрата


1.Задан прямоугольник со сторонами 20 мм и 60 мм. Вычисли его площадь. Запиши ответ в квадратных сантиметрах.

2. Был куплен дачный участок размером 20 м на 30 м. Определи площадь дачного участка, ответ запиши в квадратных сантиметрах.


Как считается площадь прямоугольника формула. Площадь прямоугольника онлайн калькулятор. Где используется расчет периметра прямоугольника

Одна из первых формул, которая изучается в математике, связана с тем, прямоугольника. Она же является и самой часто используемой. Прямоугольные поверхности окружают нас повсюду, поэтому часто требуется знать их площади. Хотя бы для того, чтобы узнать, хватит ли имеющейся в наличии краски для покраски полов.

Какие единицы измерения площади существуют?

Если говорить о той, которая принята за международную, то это будет квадратный метр. Его удобно использовать при расчете площадей стен, потолка или пола. В них указывается площадь жилья.

Когда речь идет о меньших предметах, то вводят квадратные дециметры, сантиметры или миллиметры. Последние нужны, если фигура не больше ногтя.

При измерении площади города или страны самыми подходящими оказываются квадратные километры. Но есть еще и единицы, которые используют для того, чтобы указать размер площади: ар и гектар. Первая из них еще называется соткой.

Как быть, если заданы стороны прямоугольника?

Подобным образом рассчитывается который является частным случаем прямоугольника. Так как у него все стороны равны, то произведение становится квадратом буквы а .

Как быть, если фигура изображена на клетчатой бумаге?

В этой ситуации нужно полагаться на количество клеточек внутри фигуры. По их числу бывает просто посчитать площадь прямоугольника. Но это можно сделать тогда, когда стороны прямоугольника совпадают с линиями клеток.

Часто имеет место такое положение прямоугольника, при котором его стороны наклонены по отношению к разлиновке бумаги. Тогда количество клеток определить сложно, поэтому расчет площади прямоугольника усложняется.

Потребуется сначала узнать площадь прямоугольника, который можно прочертить по клеточкам точно вокруг данного. Это просто: перемножить высоту и ширину. Потом вычесть из получившегося значения площади всех А их четыре. К слову, их рассчитывают как половину произведения катетов.

Итоговый результат даст значение площади данного прямоугольника.

Как поступить, если стороны неизвестны, зато даны его диагональ и угол между диагоналями?

До того в этой ситуации нужно вычислить его стороны, чтобы воспользоваться уже знакомой формулой. Поначалу потребуется вспомнить свойство его диагоналей. Они равны и делятся точкой пересечения пополам. Можно увидеть на чертеже, что диагонали делят прямоугольник на четыре равнобедренных треугольника, которые попарно равны друг другу.

Равные стороны этих треугольников определяются как половины диагонали, которая известна. То есть в каждом треугольнике есть две стороны и угол между ними, которые даны в задаче. Можно воспользоваться

Одна сторона прямоугольника будет вычислена по формуле, в которой фигурируют равные стороны треугольника и косинус заданного угла. Для вычисления второй значение косинуса придется брать от угла, равного разности 180 и известного угла.

Что делать, если в задаче дан периметр?

Обычно в условии указывается еще и соотношение длины и ширины. Вопрос о том, как посчитать площадь прямоугольника, в этом случае проще на конкретном примере.

Допустим, что в задаче периметр некоторого прямоугольника равен 40 см. Известно также, что его длина в полтора раза больше ширины. Необходимо узнать его площадь.

Решение задачи начинается с записи формулы периметра. Его удобнее расписать как сумму длины и ширины, каждую из которых умножить на два по отдельности. Это будет первым уравнением в системе, которую потребуется решить.

Второе связано с известным по условию соотношением сторон. Первая сторона, то есть длина, равна произведению второй (ширины) и числа 1,5. Это равенство нужно подставить в формулу для периметра.

Получится, что он равен сумме двух одночленов. Первый — произведение 2 и неизвестной ширины, второй — произведение чисел 2 и 1,5 и той же ширины. В этом уравнении всего одна неизвестная — это ширина. Нужно ее сосчитать, а потом воспользоваться вторым равенством, чтобы сосчитать длину. Останется только перемножить эти два числа, чтобы узнать площадь прямоугольника.2$.

Диагонали разделяет прямоугольник на 4 фигуры – 4 треугольника. При этом треугольники попарно равны. Если провести диагональ в прямоугольнике, то она разделяет фигуру на два равных прямоугольных треугольника.

Диагонали не является биссектрисами углов прямоугольника. А также если провести биссектрисы каждого угла, то при их пересечении получится прямоугольник.

Что мы узнали?

Мы научились находить площадь прямоугольника. Ту или иную формулы нахождения площади используют в зависимости от исходных данных. Также стоит не забывать, что если в задании разные единицы измерения сторон необходимо перевести их одну.

Тест по теме

Оценка статьи

Средняя оценка: 4.4 . Всего получено оценок: 292.

Урок на тему: «Формулы определения площади треугольника, прямоугольника, квадрата»

Дополнительные материалы
Уважаемые пользователи, не забывайте оставлять свои комментарии, отзывы, пожелания. Все материалы проверены антивирусной программой.

Обучающие пособия и тренажеры в интернет-магазине «Интеграл» для 5 класса
Тренажер к учебнику И.И.Зубаревой и А.Г.Мордковича
Тренажер к учебнику Г.В.Дорофеева и Л.Г.Петерсона

Определение и понятие площади фигуры

Чтобы лучше понять, что такое площадь фигуры, рассмотрим рисунок.
Эта произвольная фигура разбита на 12 маленьких квадратика. Сторона каждого квадратика равна 1 см. А площадь каждого квадратика равна 1 квадратному сантиметру, что записывается так: 1 см 2 .

Тогда площадь фигуры равна 12 квадратным сантиметрам. В математике площадь обозначается латинской буквой S.
Значит, площадь нашей фигуры равна: S фигуры = 12 см 2 .

Площадь фигуры равна площади всех маленьких квадратиков, из которых она состоит!

Ребята, запомните!
Площадь измеряется квадратными единицами длины. Единицы измерения площади:
1. Квадратный километр — км 2 (когда площади очень большие, например, страна или море).
2. Квадратный метр — м 2 (вполне подходит для того, чтобы измерять площадь участка или квартиры).
3. Квадратный сантиметр — см 2 (обычно используется на уроках математики, когда рисуют фигуры в тетради).
4. Квадратный миллиметр — мм 2 .

Площадь треугольника

Рассмотрим два вида треугольников: прямоугольный и произвольный.

Чтобы найти площадь прямоугольного треугольника необходимо знать длину основания и высоту. В прямоугольном треугольнике высоту заменяет одна из сторон. Поэтому в формулу площади треугольника вместо высоты подставляем одну из сторон.
В нашем примере стороны равны 7 см и 4 см. Формула для расчета площади треугольника записывается так:
S прямоугольного треугольника АВС = ВС * СА: 2


S прямоугольного треугольника АВС = 7 см * 4 см: 2 = 14 см 2

Теперь рассмотрим произвольный треугольник.

Для такого треугольника необходимо провести высоту к основанию.
В нашем примере высота равна 6 см, а основание равно 8 см. Как и в предыдущем примере, рассчитываем площадь по формуле:
S произвольного треугольника АВС = ВС * h: 2.

Подставим в формулу наши данные и получим:
S произвольного треугольника АВС = 8 см * 6 см: 2 = 24 см 2 .

Площадь прямоугольника и квадрата

Возьмем прямоугольник АВСD со сторонами 5 см и 8 см.
Формула расчета площади прямоугольника записывается так:
S прямоугольника АВСD = АВ * ВС.


S прямоугольника АВСD = 8 см * 5 см = 40 см 2 .

Теперь рассчитаем площадь квадрата. В отличии от прямоугольника и треугольника, для нахождения площади квадрата необходимо знать только одну сторону. В нашем примере сторона квадрата ABCD равна 9 см. S квадрата АВСD = АВ * ВС = АВ 2 .

Подставим в формулу наши данные и получим:
S квадрата АВСD = 9 см * 9 см = 81 см 2 .

Для вычисления площади и периметра квадрата нужно разобраться в понятиях этих величин. Квадрат представляет собой прямоугольник только с четырьмя одинаковыми сторонам, которые имеют между собой угол в 90°. Периметр — это сумма длин всех сторон. Площадь — это произведение длины прямоугольной фигуры на ее ширину.

Площадь квадрата и как ее найти

Как было сказано выше, квадрат — это прямоугольник, имеющий 4 равные стороны, поэтому ответом на вопрос: «как найти площадь квадрата» является формула: S = a*a или S = a 2 , где а — сторона квадрата. Исходя из этой формулы, легко находится сторона квадрата, если известна площадь. Для этого необходимо извлечь квадрат из указанной величины.

Например, S = 121, следовательно, а = √121 = 11. Если заданное значение отсутствует в таблице квадратов, то можно воспользоваться калькулятором: S = 94, а = √94 = 9,7.

Как найти периметр квадрата

Периметр квадрата находится по легкой формуле: Р = 4а, где а — сторона квадрата.

Пример:

  • сторона квадрата = 5, следовательно, P = 4*5 = 20
  • сторона квадрата = 3, следовательно, Р = 4*3 = 12

Но существуют такие задачи, где заведомо обозначена площадь, а нужно найти периметр. При решении нужны формулы, которые представлены ранее.

Например: как найти периметр квадрата, если известна площадь, равная 144?

Шаги решения:

  1. Выясняем длину одной стороны: а = √144 = 12
  2. Находим периметр: Р = 4*12 = 48.

Нахождение периметра вписанного квадрата


Существуют еще несколько способов нахождения периметра квадрата. Рассмотрим один из них: нахождение периметра через радиус описанной окружности. Здесь появляется новый термин «вписанный квадрат» — это квадрат, чьи вершины лежат на окружности.

Алгоритм решения:


  • так как на рассмотрении квадрат, формулу можно выразить таким образом: a 2 + a 2 = (2r) 2 ;
  • затем следует уравнение сделать проще: 2a 2 = 4(r) 2 ;
  • делим уравнение на 2: (a 2 ) = 2(r) 2 ;
  • извлекаем корень: a = √(2r).

В итоге получаем последнюю формулу: а (сторона квадрата) = √(2r).

  1. Найденная сторона квадрата умножается на 4, далее применяется стандартная формула по нахождению периметра: P = 4√(2r).

Задача:

Дан квадрат, который вписан в окружность, ее радиус равен 5. Значит, диагональ квадрата равняется 10. Применяем теорему Пифагора: 2(a 2 ) = 10 2 , то есть 2a 2 = 100. Делим полученное на два и в результате: a 2 = 50. Так как это не табличное значение, используем калькулятор: а = √50 = 7,07. Умножаем на 4: Р = 4*7,07 = 28,2. Задача решена!

Рассмотрим еще один вопрос

Часто в задачах встречается другое условие: как найти площадь квадрата, если известен периметр?

Мы уже рассмотрели все необходимые формулы, поэтому для решения задач подобного типа, необходимо умело их применять и связывать между собой. Перейдем сразу к наглядному примеру: Площадь квадрата равна 25 см 2 , найдите его периметр.

Шаги решения:

  1. Находим сторону квадрата: а = √25 = 5.
  1. Находим сам периметр: Р = 4*а = 4*5 = 20.

Подводя итог, важно напомнить, что такие легкие формулы применимы не только в учебной деятельности, но и повседневной жизни. Периметр и площадь фигуры дети учатся находить еще в начальной школе. В средних классах появляется новый предмет — геометрия, где теорема Пифагора находится в самом начале изучения. Эти азы математики проверяются и по окончанию школы ОГЭ и ЕГЭ, поэтому важно знать эти формулы и правильно их применять.

Квадрат, прямоугольник, ромб, трапеция, параллелограмм

Четырехугольник просто означает «четыре стороны»
( четырехугольник, означает четыре, боковой, означает сторону).

Четырехугольник имеет четырех сторон, , 2-мерный (плоская форма), закрытый (линии соединяются) и имеет прямых сторон.

Попробуйте сами

(также см. Интерактивные четырехугольники)

Недвижимость

В четырехугольнике:

  • четыре стороны (края)
  • четыре вершины (углы)
  • внутренние углы, которые добавляют к 360 градусов :

Попробуйте нарисовать четырехугольник и измерить углы.Они должны добавить к 360 °

Виды четырехугольников

Есть особые виды четырехугольника:

Некоторые типы также включены в определение других типов! Например, квадрат , ромб и прямоугольник также являются параллелограммами . Подробности смотрите ниже.

Давайте рассмотрим каждый вид по очереди:

Прямоугольник


маленькие квадратики в каждом углу означают «прямой угол»

Прямоугольник — это четырехсторонняя форма, каждый угол которой является прямым (90 °).

Также противоположных сторон параллельны и равной длины.

Площадь


маленькие квадратики в каждом углу означают «прямой угол»

У квадрата равные стороны (отмечены буквой «s»), и каждый угол представляет собой прямой угол (90 °)

Также противоположные стороны параллельны.

Квадрат также соответствует определению прямоугольника (все углы равны 90 °) и ромба (все стороны равной длины).

Ромб

Ромб — это четырехгранная форма, все стороны которой имеют одинаковую длину (обозначены буквой «s»).

Также противоположные стороны параллельны и противоположных углов равны.

Еще один интересный момент — диагонали (пунктирные линии) пересекаются посередине под прямым углом. Другими словами, они «рассекают» друг друга пополам под прямым углом.

Ромб иногда называют ромбом или ромбом .

Параллелограмм

У параллелограмма противоположные стороны параллельны и равны по длине. Также противоположные углы равны (углы «А» такие же, а углы «В» одинаковы).

ПРИМЕЧАНИЕ. Квадраты, прямоугольники и ромбы — это все Параллелограммы!

Пример:

Параллелограмм с:

  • все стороны равны и
  • угол «А» и «B» как прямые углы

— это квадрат !

Трапеция (UK: Trapezium)

Трапеция

Равнобедренная трапеция

Трапеция (в Великобритании ее называют трапецией) имеет пару параллельных противоположных сторон.

И трапеция (в Великобритании она называется трапецией) — четырехугольник без параллельных сторон:

Трапеция Трапеция
В США: Пара параллельных сторон НЕТ параллельных сторон
В Великобритании: НЕТ параллельных сторон Пара параллельных сторон
(определения для США и Великобритании поменяны местами!)

Равнобедренная трапеция , как показано выше, имеет левую и правую стороны равной длины, которые соединяются с основанием под равными углами.

Воздушный змей

Эй, это похоже на воздушного змея (обычно).

Имеет две пары сторон:

Каждая пара состоит из двух соединяющихся сторон равной длины.

Также:

  • углы, где встречаются две пары равны.
  • диагонали, показанные выше пунктирными линиями, пересекаются в под прямым углом.
  • одна из диагоналей делит пополам (делит пополам) другую.

… вот и все специальные четырехугольники.

Неправильные четырехугольники

Единственный правильный четырехугольник (все стороны равны и все углы равны) — это квадрат. Итак, все остальные четырехугольники неправильные .

Схема «Генеалогическое древо»

Определения четырехугольника: , включая .

Пример: квадрат также является прямоугольником.

Итак, мы включаем квадрат в определение прямоугольника.

(Мы, , не говорим : «Наличие всех углов 90 ° делает его прямоугольником, кроме случаев, когда все стороны равны, тогда это квадрат».)

Это может показаться странным, поскольку в повседневной жизни мы думаем о квадрате как о , а не о как о прямоугольнике … но в математике это .

Используя приведенную ниже таблицу, мы можем ответить на такие вопросы, как:

  • Квадрат — это тип прямоугольника? (Да)
  • Прямоугольник — это разновидность воздушного змея? (Нет)

Сложные четырехугольники

О да! когда две стороны пересекаются, мы называем это «сложным» или «самопересекающимся» четырехугольником, например:

У них все еще есть 4 стороны, но две стороны пересекаются.

Многоугольник

Четырехугольник — это многоугольник. На самом деле это четырехсторонний многоугольник, точно так же, как треугольник — это трехсторонний многоугольник, пятиугольник — пятисторонний многоугольник и так далее.

Играйте с ними

Теперь, когда вы знаете различные типы, вы можете поиграть с интерактивными четырехугольниками.

Другие названия

Четырехугольник иногда можно назвать:

  • a Quadrangle (« четыре угла »), поэтому звучит как «треугольник»
  • a Tetragon (« четыре многоугольника »), поэтому это звучит как «пятиугольник», «шестиугольник» и т. Д.

621 622 623 624 763 764, 2128, 2129, 3230, 3231

Геометрические формы и типы фигур

Что такое геометрические плоские формы ? Какие у них характеристики? Это вопросы, на которые мы ответим в этом посте.

основных геометрических плоских формы :

Круг

Окружность — это форма, которую можно создать, отслеживая кривую, которая всегда находится на одинаковом расстоянии от точки, которую мы называем центром.Расстояние по окружности называется окружностью окружности.

Треугольник

Треугольник — это форма, образованная 3 прямыми линиями, которые называются сторонами. Существуют разные способы классификации треугольников по их сторонам или углам.

  1. По углам:
  • Прямой треугольник: наибольший из трех углов является прямым.
  • Острый треугольник: самый большой из трех углов — это острый угол (менее 90 градусов).
  • Тупой треугольник: самый большой из трех углов — тупой угол (более 90 градусов).

2. По сторонам:

  • Равносторонний треугольник: все 3 стороны одинаковой длины.
  • Равнобедренный треугольник: у него 2 (или более) стороны равной длины. (Равносторонний треугольник тоже равнобедренный.)
  • Чешуйчатый треугольник: нет двух равных сторон.

Прямоугольник

Прямоугольник — это фигура с 4 сторонами.Отличительной особенностью прямоугольника является то, что все четыре угла составляют 90 градусов.

Ромб

Ромб представляет собой форму, образованную 4 прямыми линиями. Его четыре стороны имеют одинаковую длину, но, в отличие от прямоугольника, любой из четырех углов составляет 90 градусов.

Квадрат

Квадрат — это разновидность прямоугольника, но также разновидность ромба. У него есть характеристики обоих из них.То есть все 4 угла — прямые, а все 4 стороны равны по длине.

Трапеция

Трапеция также имеет 4 стороны. У него две стороны, которые параллельны, а две другие — нет.

Вы можете попрактиковаться с геометрическими плоскими формами, зарегистрировавшись в Smartick.

Подробнее:

Команда по созданию контента.
Многопрофильная и многонациональная команда, состоящая из математиков, учителей, профессоров и других специалистов в области образования!
Они стремятся создавать максимально качественные математические материалы.

9 самых распространенных форм и способы их определения

Вы, наверное, много узнали о формах, даже не задумываясь о том, что они из себя представляют. Но понимание того, что такое форма, невероятно удобно при сравнении ее с другими геометрическими фигурами, такими как плоскости, точки и линии.

В этой статье мы рассмотрим, что такое фигура, а также множество общих фигур, как они выглядят и основные формулы, связанные с ними.

Что такое форма?

Если вас спросят, что такое форма, вы, вероятно, сможете назвать довольно много из них. Но «форма» тоже имеет особое значение — это не просто названия кругов, квадратов и треугольников.

Форма — это форма объекта, а не то, сколько места он занимает или где находится физически, а реальную форму, которую он принимает. Круг определяется не тем, сколько места он занимает или где вы его видите, а скорее реальной круглой формой, которую он принимает.

Форма может иметь любой размер и появляться где угодно; они ничем не ограничены, потому что фактически не занимают места.Трудно осознать это, но не думайте о них как о физических объектах — форма может быть трехмерной и занимать физическое пространство, например подставку для книг в форме пирамиды, цилиндрическую банку с овсянкой или он может быть двухмерным и не занимать физического пространства , такого как треугольник, нарисованный на листе бумаги.

Тот факт, что он имеет форму, отличает форму от точки или линии.

Точка — это просто позиция; у него нет ни размера, ни ширины, ни длины, ни вообще никаких размеров.

Линия же одномерная. Он бесконечно тянется в любом направлении и не имеет толщины. Это не форма, потому что у нее нет формы.

Хотя мы можем представлять точки или линии как фигуры, потому что нам действительно нужно их видеть, на самом деле они не имеют никакой формы. Это то, что отличает форму от других геометрических фигур — она ​​двух- или трехмерная, потому что у нее есть форма.

Кубики, подобные тем, что здесь изображены, представляют собой трехмерные формы квадратов — обе формы!

Шесть основных типов двумерных геометрических форм

Трудно изобразить форму только на основе определения — что значит иметь форму и , но не занимать места? Давайте взглянем на несколько различных форм, чтобы лучше понять, что именно значит быть формой!

Мы часто классифицируем формы по количеству сторон. «Сторона» — это линейный сегмент (часть линии), составляющий часть фигуры. Но у фигуры тоже может быть неоднозначное количество сторон.

Тип 1: эллипсы

Эллипсы — это круглые, овальные формы, в которых заданная точка ( p ) имеет одинаковую сумму расстояний от двух разных фокусов.

овал

Овал немного похож на размазанный круг — он не совсем круглый, а в некотором роде вытянутый. Однако классификация неточная.Существует много-много видов овалов, но общее значение состоит в том, что они имеют круглую форму, которая имеет удлиненную форму, а не идеально круглую, как круг. Овал — это любой эллипс, фокусы которого находятся в двух разных положениях.

Поскольку овал не является идеально круглым, формулы, которые мы используем для их понимания, должны быть скорректированы.

Также важно отметить, что вычислить окружность овала довольно сложно , поэтому ниже нет уравнения окружности.Вместо этого используйте онлайн-калькулятор или калькулятор со встроенной функцией окружности, потому что даже лучшие уравнения окружности, которые вы можете составить вручную, являются приблизительными.

Определения

  • Большой радиус : расстояние от начала овала до самого дальнего края
  • Малый радиус : расстояние от начала овала до ближайшего края
Формулы
  • Площадь = $ \ Major \ Radius * \ Minor \ Radius * π $

Круг

Сколько сторон у круга? Хороший вопрос! К сожалению, нет хорошего ответа, потому что «стороны» больше связаны с многоугольниками — двумерной формой, по крайней мере, с тремя прямыми сторонами и обычно, по крайней мере, с пятью углами. Наиболее знакомые формы — это многоугольники, но у кругов нет прямых сторон и определенно нет пяти углов, поэтому они не являются многоугольниками.

Итак, сколько сторон у круга? Нуль? Один? На самом деле это неуместно — вопрос просто не относится к кругам.

Круг — это не многоугольник, но что это такое? Круг — это двумерная форма (у нее нет толщины и глубины), состоящая из кривой, которая всегда находится на одинаковом расстоянии от точки в центре. У овала два фокуса в разных положениях, тогда как у круга фокусы всегда находятся в одном и том же положении.

Определения

  • Начало: центр окружности
  • Радиус: расстояние от начала координат до любой точки на окружности
  • Окружность: расстояние по окружности
  • Диаметр: длина от одного края круга до другого
  • $ \ bo {π} $: (произносится как пирог) 3.2 $

Тип 2: Треугольники

Треугольники — это простейшие многоугольники. У них три стороны и три угла, но они могут отличаться друг от друга. Возможно, вы слышали о прямоугольных или равнобедренных треугольниках — это разные типы треугольников, но все они имеют три стороны и три угла.


Поскольку существует много видов треугольников, есть лотов важных формул треугольников , многие из них более сложные, чем другие.Основы включены ниже, но даже основы полагаются на знание длины сторон треугольника. Если вы не знаете стороны треугольника, вы все равно можете рассчитать его различные аспекты, используя углы или только некоторые из сторон.

Определения

  • Вершина : точка пересечения двух сторон треугольника
  • Основание : любая из сторон треугольника, обычно та, которая нарисована внизу.
  • Высота : расстояние по вертикали от основания до вершины, с которой она не связана.

Формулы

  • Площадь = $ {\ base * \ height} / 2 $
  • Периметр = $ \ side a + \ side b + \ side c $

Тип 3: параллелограммы

Параллелограмм — это форма с равными противоположными углами, параллельными противоположными сторонами и параллельными сторонами равной длины. Вы могли заметить, что это определение применяется к квадратам и прямоугольникам — это потому, что квадрата и прямоугольника также являются параллелограммами ! Если вы можете вычислить площадь квадрата, вы можете сделать это с любым параллелограммом.

Определения

  • Длина : размер нижней или верхней стороны параллелограмма
  • Ширина : размер левой или правой стороны параллелограмма

Формулы

  • Область : $ \ length * \ height $
  • Периметр : $ \ Сторона 1 + \ Сторона 2 + \ Сторона 3 + \ Сторона 4 $
  • Или Периметр : $ \ Side * 4 $
Прямоугольник

Прямоугольник — это фигура с параллельными противоположными сторонами в сочетании со всеми углами в 90 градусов. Как тип параллелограмма, он имеет противоположные параллельные стороны. В прямоугольнике одна группа параллельных сторон длиннее другой, что делает его похожим на удлиненный квадрат.


Поскольку прямоугольник является параллелограммом, вы можете использовать те же формулы для вычисления их площади и периметров.

Квадрат

Квадрат во многом похож на прямоугольник, за одним заметным исключением: все его стороны равны по длине. Как и прямоугольники, квадрата имеют углы 90 градусов и параллельны противоположным сторонам. Это потому, что квадрат на самом деле является разновидностью прямоугольника, который является разновидностью параллелограмма!

По этой причине вы можете использовать те же формулы для вычисления площади или периметра квадрата, как и для любого другого параллелограмма.

Ромб

Ромб — как вы уже догадались — разновидность параллелограмма. Разница между ромбом и прямоугольником или квадратом в том, что его внутренние углы на равны только , как их диагональные противоположности.

Из-за этого, ромб немного похож на квадрат или прямоугольник, немного скошенный в сторону . Хотя периметр рассчитывается таким же образом, это влияет на способ вычисления площади, потому что высота больше не такая, как в квадрате или прямоугольнике.

Определение

  • Диагональ : длина между двумя противоположными вершинами

Формулы

  • Площадь = $ {\ Диагональ 1 * \ Диагональ 2} / 2 $

Тип 4: трапеции

Трапеции — это четырехгранные фигуры с двумя противоположными параллельными сторонами.В отличие от параллелограмма трапеция имеет только две противоположные параллельные стороны, а не четыре , что влияет на способ вычисления площади и периметра.

Определения

  • Основание : любая из параллельных сторон трапеции
  • Ноги : одна из непараллельных сторон трапеции
  • Высота : расстояние от одной базы до другой

Формулы

  • Область : $ ({\ Base_1 \ length + \ Base_2 \ length} / 2) \ altitude $
  • Периметр : $ \ Base + \ Base + \ Leg + \ Leg $

Тип 5: Пятиугольники

Пятиугольник — это пятиугольник. Обычно мы видим правильные пятиугольники, у которых все стороны и углы равны , но существуют и неправильные пятиугольники. Неправильный пятиугольник имеет неравные стороны и неравные углы и может быть выпуклым — без углов, направленных внутрь, или вогнутым — с внутренним углом больше 180 градусов.

Поскольку форма более сложная, ее необходимо разделить на более мелкие формы, чтобы вычислить ее площадь.

Определения

  • Апофема : линия, проведенная от центра пятиугольника к одной из сторон, ударяющая в сторону под прямым углом.

Формулы

  • Периметр : $ \ Сторона 1 + \ Сторона 2 + \ Сторона 3 + \ Сторона 4 + \ Сторона 5 $
  • Площадь : $ {\ Perimeter * \ Apothem} / 2 $

Тип 6: шестиугольники

Шестиугольник — это шестигранная форма, очень похожая на пятиугольник. Чаще всего мы видим правильные шестиугольники, но они, как и пятиугольники, также могут быть неправильными, выпуклыми или вогнутыми.

Так же, как и пятиугольники, формула площади шестиугольника значительно сложнее, чем формула параллелограмма.

Формулы

  • Периметр : $ \ Сторона 1 + \ Сторона 2 + \ Сторона 3 + \ Сторона 4 + \ Сторона 5 + \ Сторона 6 $
  • Площадь : $ {3√3 * \ Side * 2} / 2 $
  • В качестве альтернативы, Площадь : $ {\ Perimeter * \ Apothem} / 2 $

А как насчет трехмерных геометрических фигур?

Существуют также трехмерные формы, которые имеют не только длину и ширину, но также глубину или объем. Это формы, которые вы видите в реальном мире, такие как сферический баскетбольный мяч, цилиндрический контейнер с овсянкой или прямоугольная книга.

Трехмерные формы, естественно, более сложные, чем двухмерные, с дополнительное измерение — объем занимаемого пространства, а не только форма, — которое необходимо учитывать при вычислении площади и периметра.

Математика

, включающая двумерные формы, такие как приведенные выше, называется плоской геометрией , потому что она имеет дело конкретно с плоскостями или плоскими формами . Математика, включающая трехмерные формы, такие как сферы и кубы, называется твердотельной геометрией , потому что она имеет дело с твердыми телами, другим словом для трехмерных фигур .

Двухмерные формы составляют трехмерные формы, которые мы видим каждый день!

3 основных совета по работе с фигурами

Существует так много типов фигур, что бывает сложно запомнить, что есть что, и как рассчитать их площади и периметры. Вот несколько советов и приемов, которые помогут вам их запомнить!

# 1: Определить многоугольники

Некоторые формы являются многоугольниками, а некоторые нет. Один из самых простых способов определить тип фигуры — это определить, является ли это многоугольником.

Многоугольник состоит из прямых, не пересекающихся. Какие фигуры ниже являются многоугольниками, а какие нет?

Круг и овал не являются многоугольниками, поэтому их площадь и периметр рассчитываются по-разному. Узнайте больше о том, как вычислить их с помощью $ π $ выше!

# 2: Проверить параллельность сторон

Если фигура, на которую вы смотрите, представляет собой параллелограмм, обычно легче вычислить ее площадь и периметр, чем если бы это не параллелограмм. Но как определить параллелограмм?

Это прямо в названии — параллель. Параллелограмм — это четырехсторонний многоугольник с двумя наборами параллельных сторон . Квадраты, прямоугольники и ромбы — это параллелограммы.

Квадраты и прямоугольники используют одни и те же базовые формулы для вычисления площади длины, умноженной на высоту. Их также очень легко найти по периметру, поскольку вы просто складываете все стороны вместе.

С ромбами все усложняется, потому что вы умножаете диагонали и делите их на два.

Чтобы определить, на какой параллелограмм вы смотрите, спросите себя, все ли у него углы 90 градусов.

Если да, то это квадрат или прямоугольник . Прямоугольник имеет две стороны, которые немного длиннее других, тогда как у квадрата все стороны равны. В любом случае, вы вычисляете площадь, умножая длину на высоту и периметр, складывая все четыре стороны вместе.

Если нет, вероятно, это ромб, который выглядит так, как если бы вы взяли квадрат или прямоугольник и наклонили его в любом направлении. В этом случае вы найдете площадь, умножив две диагонали вместе и разделив на два. Периметр определяется так же, как периметр квадрата или прямоугольника.

# 3: Подсчитайте количество сторон

Формулы для фигур, у которых нет четырех сторон, могут быть довольно сложными, поэтому лучше всего их запомнить. Если у вас возникли проблемы с их правильностью, попробуйте запомнить греческие слова для чисел, , например:

Tri : три, как в triple, что означает три чего-то

Tetra : четыре, как количество квадратов в блоке Tetris

Penta : пять, как в Пентагоне в Вашингтоне Д.C., представляющий собой большое здание в форме Пентагона

.

Hexa : шесть, как в шестнадцатеричном формате, шестизначные коды, часто используемые для цвета в веб-дизайне и графическом дизайне

Септа : семь, как в Септе, женском духовенстве религии Игры Престолов, имеющей семь богов

Octo : восемь, как в восьми лапах осьминога

Эннеа : девять, как в эннеаграмме, общая модель человеческих личностей

Дека : десять, как в десятиборье, в котором спортсмены завершают десять видов

Что дальше?

Если вы готовитесь к ACT и вам нужна дополнительная помощь по геометрии, ознакомьтесь с этим руководством по координатной геометрии!

Если вы больше относитесь к типу SAT, это руководство по треугольникам в разделе геометрии SAT поможет вам подготовиться к тесту !

Не можете насытиться математикой ACT? Это руководство по полигонам на ACT поможет вам подготовиться с помощью полезных стратегий и практических задач!

Квадрат — это прямоугольник? Классификация фигур — Доктора математики

Мы получаем много вопросов о классификации фигур как от учеников начальной, так и от старшей школы (или их родителей или учителей).У них часто возникают проблемы с самой идеей классификации предметов путем применения определений, а также с тем фактом, что определения могут варьироваться как в повседневном, так и в техническом использовании, а также от одного учебника к другому.

X — это Y? Может ли X быть Y?

Мы видим этот вопрос в нескольких формах:

  • Квадрат — это прямоугольник?
  • Может ли прямоугольник быть квадратом?
  • Все ли квадраты прямоугольные?

Я обнаружил, что многие студенты борются с самой формой вопроса, а также с определениями, о которых он спрашивает: спрашивают ли нас, является ли каждый квадрат прямоугольником или просто конкретный квадрат является прямоугольником. прямоугольник? Большая часть трудности заключается в том, что дети не привыкли к техническому языку, где детали формулировки важны.Возможно, им потребуется показать, что, например, «X — Y?» означает: «Является ли каждые X Y?» (или «Является ли X всегда Y?»), а не «Является ли некоторым X Y?». С другой стороны, «Может ли X быть Y?» означает: « какой-то X a Y?» (или «Есть ли какие-либо X, которые являются Y?»), а не «Возможно ли, что каждые X являются Y?». На гораздо более продвинутом уровне мы будем говорить об «универсальных и экзистенциальных кванторах»; но даже базовый язык сложен для непосвященных.

Вот типичный вопрос, с 2004 года:

 Квадраты - это прямоугольники? Прямоугольники квадраты?

Может ли прямоугольник быть квадратом? Мне просто было интересно, потому что квадрат может быть прямоугольником, но  может ли прямоугольник быть квадратом?

Из комментариев Алисы следует, что она не понимает слова «может», как я сказал выше, но не имеет проблем с представлением квадратов как прямоугольников. Итак, я начал с уточнения формулировки и идеи классификации:

 Привет, Алиса.На самом деле КАЖДЫЙ квадрат - это прямоугольник, поскольку углы в квадрате всегда прямые. Это больше, чем сказать, что квадрат МОЖЕТ быть прямоугольником; Это.

А поскольку квадраты являются прямоугольниками, вы знаете, что некоторые прямоугольники являются квадратами, а именно квадраты!

Эти идеи сбивают с толку многих. Возможно, стоит подумать о других категориях, например о собаках и животных. Может ли собака быть животным? Конечно же - каждая собака - животное! Может ли животное быть собакой? Да, если вы посмотрите на собаку, это животное, то есть собака.Но не каждое животное - собака. Почти глупо задавать эти вопросы и отвечать на них.

Затем я перешел к другому вопросу, который может беспокоить или не беспокоить Алису: в этой классификации слова используются иначе, чем в повседневной речи:

 С квадратами и прямоугольниками это звучит менее глупо, но идея та же. Проблема в том, что в повседневной жизни  мы обычно используем слово «прямоугольник» для обозначения неквадратов , потому что, если бы форма была квадратом, мы бы назвали это так.Поэтому мы учим детей «это прямоугольник, это квадрат - стороны прямоугольника разной длины». Но когда вы вырастете, , важно думать о квадрате как о СПЕЦИАЛЬНОМ прямоугольнике , потому что это все, что есть прямоугольник, и многое другое.

Это как если бы кто-то посмотрел на вашу собаку и сказал: «Какое у вас прекрасное животное!», А вы ответили: «Это не животное - это породистый лабрадор-ретривер». Для вас важен конкретный вид животного, потому что он особенный; но на самом деле это тоже животное.А квадрат по-прежнему остается прямоугольником, но это не ПРОСТО прямоугольник, это квадрат (породистый).

Вы видите в этом суть? Мы используем такие слова, как «прямоугольник» или «собака», двояко: иногда мы хотим что-то конкретно идентифицировать (используя наиболее точный термин, который мы можем: «дайте мне квадрат, а не простой прямоугольник»; «это моя собака, а не просто животное »). С другой стороны, иногда мы хотим только поместить его в общую категорию (этот квадрат является прямоугольником, потому что у него прямые углы; эта собака — животное, потому что она дышит).Прямоугольник — это любая четырехгранная фигура со всеми прямыми углами; Квадрат — это прямоугольник особого вида , а именно тот, стороны которого также имеют одинаковую длину. Это более сложный взгляд на слова.

Опять же, собака ( любая собака ) — это животное; животное ( некоторые из конкретных животных) может быть собак.

Как может быть и то, и другое?

Вот вопрос 2006 года, ставящий под сомнение определение:

 Классифицирующие четырехугольники

Мой учитель говорит, что квадрат  - это также прямоугольник .Не понимаю, как такое может быть, ведь стороны одинаковой длины.

Обеспокоенность Адриенн выходит за рамки значения «квадрат — это прямоугольник», до конкретного определения; ее слово «также» предполагает, что она думает, что у чего угодно может быть только один ярлык. Для нее прямоугольник должен быть фигурой, стороны которой имеют разную длину, поэтому квадрат нельзя назвать прямоугольником. На этот раз я немного углубился в природу определений, но начал с тех же идей (обратите внимание, как старая шутка соответствует моему комментарию о породистой собаке):

 В повседневном использовании мы указываем на квадрат и говорим: «Это квадрат, а не прямоугольник.«Это потому, что мы обычно называем все как можно более конкретно.« Это не дама, это моя жена! »

В математике и естественных науках у нас немного другой взгляд на слова: мы хотим, чтобы каждый термин применялся ко всему, для чего он имеет смысл, и мы хотим, чтобы каждое определение было как можно более простым. Так, например, мы определяем прямоугольник просто как «фигуру с четырьмя прямыми сторонами, все углы которых являются прямыми углами». Если вы сравните квадрат с этим определением, вы увидите, что он подходит: у него есть четыре стороны и четыре прямых угла.Итак, это прямоугольник. Конечно, это БОЛЬШЕ, чем прямоугольник; Помимо требований, предъявляемых к прямоугольнику, у него также есть четыре РАВНЫЕ стороны. Но это не делает его НЕ прямоугольником, а только более СПЕЦИАЛЬНЫМ прямоугольником.

Мы делаем такие определения (называемые «включающими определениями») не зря. Когда мы формулируем теорему о прямоугольниках, мы хотим иметь возможность применять ее во всех случаях, когда она верна. Поскольку любой факт о форме, зависящий только от того факта, что она имеет прямые углы, будет применяться не только к «простым прямоугольникам», но и к квадратам (специальным прямоугольникам), имеет смысл использовать одно слово, чтобы охватить их все, а не одно слово обозначает «неквадратные прямоугольники», а другое - квадраты.По крайней мере, это значительно упрощает формулирование теорем.

То же самое и в других областях науки. Мы используем инклюзивные определения при именовании животных, например: терьер - это особый вид собак, собака - особый вид млекопитающих, а млекопитающее - особый вид позвоночных. Вы бы не сказали «это терьер, а не млекопитающее» только потому, что «терьер» - более конкретный термин, чем «млекопитающее»; нам нужно иметь слово, охватывающее всех млекопитающих, чтобы мы могли говорить о фактах, которые верны в отношении всех них.Точно так же квадрат - это просто разновидность прямоугольника.

Это ключевая идея классификации: чтобы создать иерархию категорий, каждая должна включать категорий. В результате мы склонны определять вещи на основе свойств, которые они имеют (например, прямые углы), а не на свойствах, которых не имеет (например, равные стороны). Таким образом, все, что имеет определенные свойства, относится к категории, независимо от того, что еще к ней относится.

Я продолжил, иллюстрируя эту идею схемой классификации четырехугольников:

 Так же, как мы можем составить целое дерево классификации животных, мы можем классифицировать формы, используя эти включающие имена.Вот классификация основных видов четырехугольников (четырехугольников):

            четырехугольник
              / \
             / \
            / \
          воздушный змей трапеция
           | / \
           | / \
           | / \
           | параллелограмм равнобедренный
           | / \ трапеция
           | / \ /
           | / \ /
         ромб прямоугольник
              \ /
               \ /
                \ /
                 квадрат

Каждый рисунок - это частный случай рисунка (ов) над ним.Без исчерпывающего наименования нам пришлось бы написать теоремы вроде «если вы соедините середины последовательных сторон четырехугольника, воздушного змея, трапеции, параллелограмма, ромба, прямоугольника или квадрата, то полученная фигура будет параллелограммом, ромбом, прямоугольником или квадратом. . " Используя инклюзивные определения, теорема просто «если вы соедините середины последовательных сторон четырехугольника, то полученная фигура будет параллелограммом». Это спасает много деревьев!

Например, у ромба четыре равные стороны; прямоугольник имеет четыре перпендикулярные стороны; квадрат имеет четыре равные перпендикулярные стороны, так что это и ромб и прямоугольник, а также параллелограмм и даже трапеция, потому что любой прямоугольник тоже подходит под эти определения.[Если вы усомнитесь в этом последнем утверждении, мы в конце концов доберемся до него!]

Вот два более коротких ответа, касающихся квадрата и ромба:

 Сравнение ромба и квадрата

Может ли ромб быть квадратом?

Конфликтующие определения

Важно понимать, что оба определения используются в разных контекстах; математики обычно используют инклюзивные определения, но в элементарных учебниках иногда используются менее технические эксклюзивные определения, предположительно потому, что они больше нацелены на обучение повседневному использованию, чем на подготовку к теоретической математике.Вот еще один вопрос, очень похожий на другие:

 Включительное и эксклюзивное определения

Квадраты - это прямоугольники? Прямоугольники квадраты?

Доктор Флор ответил на этот вопрос, сделав акцент на возможных разногласиях:

 Прямоугольники не всегда являются квадратами, потому что у квадратов должны быть четыре стороны равной длины. Вопрос о том, верно ли обратное, зависит от того, какое определение вы используете. По поводу определений часто возникают споры.

В общем, существует два типа определения геометрических фигур:

ВКЛЮЧИТЕЛЬНЫЕ ОПРЕДЕЛЕНИЯ: В случае прямоугольников и квадратов это означает, что квадрат рассматривается как частный случай прямоугольника:
* Прямоугольник - это четырехугольник с четырьмя
  прямые углы.* Квадрат - это четырехугольник с четырьмя
  прямые углы и четыре равные стороны.

ИСКЛЮЧИТЕЛЬНЫЕ ОПРЕДЕЛЕНИЯ: В случае прямоугольников и квадратов это означает, что квадрат НЕ считается прямоугольником:
* Прямоугольник - это четырехугольник с четырьмя
  под прямым углом, но не с четырьмя равными сторонами.
* Квадрат - это четырехугольник с четырьмя
  прямые углы и четыре равные стороны.

Я предпочитаю инклюзивные определения, потому что они включают в себя базовое математическое понятие «обобщение»: один элемент (прямоугольник) является более общим, чем другой элемент (квадрат).Но другие говорят, что эксклюзивные определения очень полезны в особых случаях.

Для краткого изучения того, что настоящие словари говорят об этих определениях, см. Это обсуждение, где учитель настаивал на исключительном определении:

 Включающие и эксклюзивные определения

Равносторонний треугольник равнобедренный?

Почти одновременно Мишель задала связанный с этим вопрос о треугольниках, который был заархивирован вместе с последним. Ее смущало то, что разные источники давали разные ответы:

 Я учусь в 10 классе, и мне нужно знать, имеет ли равнобедренный треугольник ровно или только две стороны совпадающие.Считается ли равносторонний треугольник равнобедренным? Я просмотрел более 30 сайтов, но так и не получил полного ответа о том, совпадают ли точно, только или, по крайней мере, 2 стороны, - а если да, то нет никаких объяснений или доводов, подтверждающих это утверждение.

Если мы определим равнобедренный треугольник как треугольник, в котором ровно (только) две стороны имеют одинаковую длину, то он не включает равносторонние треугольники. Мы так думаем. Но исчерпывающее определение состоит в том, что , по крайней мере, двух сторон конгруэнтны, так что он включает в себя треугольники, у которых более двух сторон одинаковой длины.

Доктор Шва ответил на озабоченность Мишель, объяснив , почему инклюзивное определение лучше в математике:

 Привет, Мишель,

Вопрос о том, должен ли равнобедренный треугольник иметь по крайней мере две конгруэнтные стороны или ровно две конгруэнтные стороны, нельзя доказать: это вопрос определения. Что означает термин «равнобедренный треугольник»?

  Определения - это то, что мы можем выбирать произвольно, и книги могут иметь разные определения.

  Однако некоторые определения более полезны, чем другие , более удобны, проще в использовании ... и в этом случае один из этих двух вариантов определения намного лучше, чем другой. Инклюзивное определение почти всегда лучше, как в данном случае. Инклюзивное определение, в котором равнобедренные треугольники включают равносторонние треугольники, намного удобнее. Таким образом, равнобедренные треугольники следует определять как треугольники, у которых * как минимум * две стороны совпадают.

Почему инклюзивное определение удобнее? Что ж, рассмотрим теорему вроде:

   Если угол A = угол B в треугольнике ABC, то треугольник равен
   равнобедренный.Если бы у вас было неисключающее определение, вам всегда приходилось бы говорить такие вещи, как:

   Если угол A = угол B, но не равен углу C, то ...

или

   Если ... то треугольник равнобедренный или равносторонний.

По той же причине определение прямоугольника должно включать квадраты, определение параллелограмма должно включать прямоугольники и так далее. Инклюзивное определение почти всегда лучше.

Давайте посмотрим на еще одно обсуждение этого от учителя:

 Равносторонний треугольник тоже равнобедренный?

Можно ли классифицировать равносторонние треугольники как равнобедренные?

В нашем учебнике по математике для 6-х классов равнобедренный треугольник определяется как «треугольник с как минимум двумя равными сторонами.«Использование по крайней мере» подразумевает, что равносторонний треугольник также может быть классифицирован как равнобедренный, поскольку у него «по крайней мере» две равные стороны (возможно, аналогично тому, как квадрат также является прямоугольником?)

Будучи студентом, я всегда знал, что три типа треугольников при классификации по длине стороны (равносторонние, равнобедренные и разносторонние) были разными и отдельными. Равносторонний треугольник имеет 3 равные стороны, равнобедренный - 2, а разносторонний треугольник имеет разную длину для каждой стороны.Учебник нашей школы заставил меня усомниться в этом предположении, поэтому я зашел на ваш сайт! Я не хочу учить этому неправильно!

Что правильно? Можно ли считать равносторонний треугольник равнобедренным?

Это возвращает нас обратно к нашей старой идее о том, что нам нужны инклюзивные определения теорем, но эксклюзивные определения, когда нам нужно идентифицировать что-то как можно точнее, например нашу любимую собаку. Доктор Рик указал, что это необходимый переход от вводного использования термина к более зрелому математическому использованию:

 Привет, Карен.Я определенно предпочитаю всеобъемлющее определение, использующее «по крайней мере». Да, это то же самое, что сказать, что квадрат - это разновидность прямоугольника; Равносторонний треугольник - это разновидность равнобедренного треугольника.

Я рад, что ваш учебник идет в этом направлении; так думают математики. К тому времени, когда студенты пойдут на урок геометрии, на котором они научатся доказывать теоремы, я надеюсь, что они выучат инклюзивные определения, потому что они соответствуют принципу работы теорем.Теорема, которая верна для любого прямоугольника, применима к квадрату, потому что квадрат соответствует определению прямоугольника; для квадратов писать отдельную теорему не нужно. Точно так же теорема, которая верна для любого равнобедренного треугольника, также применима к равносторонним треугольникам, потому что они соответствуют определению равнобедренного треугольника.

Так почему бы не научиться такому мышлению в шестом классе? Мне приятно это слышать!

В другом (неархивированном) ответе доктор Рик затронул вопрос о том, что делать, если в учебнике используется «неправильное» определение:

 Однако факт в том, что любая приличная книга по математике дает свои собственные определения терминов, и выбор автора является законом в контексте этой книги.Если в книге равнобедренный треугольник определяется как треугольник с * ровно * двумя равными сторонами, это определение равнобедренного треугольника всякий раз, когда вы находите слово, использованное в этой книге. Хотя мы можем предпочесть другое определение, мы должны принять определение, используемое в книге, и понимать все, что говорится о равнобедренных треугольниках, в свете этого определения. Это одно из решений путаницы. Я надеюсь, что это помогает.

Это важная вещь, которую нужно знать об определениях: математик может свободно указывать, как он будет использовать слово, и такое «локальное» определение отменяет любые вопросы о том, что является «стандартным».Конечно, это будет сделано только тогда, когда не будет общепринятого стандарта.

Об определениях форм можно сказать больше; в будущем я еще вернусь к этому, рассматривая трапеции и «ромбы», среди прочего.

Разница между квадратом и прямоугольником

Что такое двумерные формы?

Двумерная фигура определяется как плоская фигура. Это плоская фигура, которая обычно имеет два измерения: длину и ширину.У этих фигур нет толщины или глубины. Есть много разных типов двумерных фигур. И квадрат, и прямоугольник — это двухмерные формы, имеющие только длину и ширину.

2D-фигуры могут иметь разные характеристики, которые помогают нам различать и определять каждую форму отдельно. И квадрат, и прямоугольник имеют разные характеристики, которые помогают нам различать их.


Что такое прямоугольник?

Прямоугольник — это двухмерная фигура с четырьмя сторонами.Прямоугольник состоит из четырех прямых линий, образующих угол 90 градусов. Это называется четырехугольником. Четырехугольник — это плоская фигура с четырьмя сторонами. У него четыре угла, четыре стороны и четыре вершины (точки пересечения ребер). На рисунке ниже показан прямоугольник с вершинами A, B, C и D. Стороны — AD, DC, CB и BA, а диагонали — AC и DB. Диагонали пересекаются в точке R.

(изображение скоро будет загружено)

Каковы характеристики прямоугольника?

1.Противоположные стороны параллельны:

Любые две противоположные стороны прямоугольника будут параллельны. В приведенном выше случае AD и BC параллельны, а AB и DC параллельны.


2. Противоположные стороны равны:

Противоположные стороны прямоугольника равны. На рисунке, если AD имеет длину 5 см, то противоположная сторона, то есть BC, также имеет длину 5 см.


3. Все углы прямые, т.е. 90 градусов:

В прямоугольнике углы, образованные сторонами, являются прямыми углами.Следовательно, всего имеется четыре угла по 90 градусов. Итак, ADC, ∠DCB, ∠CBA и ∠BAD имеют угол 90 градусов каждый.

4. Смежные углы являются дополнительными:

Смежные означает пару углов, которые образуются на одной стороне прямой линии, особенно когда одна сторона встречается или пересекается с другой линией. Соседние углы прямоугольника являются дополнительными, т.е. в сумме они составляют 180 градусов.


5. Диагонали равны:

Диагонали — это прямые линии, проведенные от одного угла до противоположного.На рисунке BD и AC — диагонали одинаковой длины.

6. Диагонали делят пополам:

Диагонали прямоугольника пересекаются в точке, где они будут делить пополам. Деление пополам означает разделение линии на две равные половины. На рисунке AC и BD пересекаются в точке R, которая делит диагонали пополам. Итак, если AC и BD по 8 см, AR, DR, CR и BR по 4 см.


Что такое квадрат?

Квадрат — это четырехугольник с четырьмя сторонами.Все эти четыре стороны равны. Подобно прямоугольнику, все стороны квадрата встречаются под углом 90 градусов. Давайте посмотрим на рисунок ниже:

(изображение будет загружено в ближайшее время)

Здесь четыре стороны — AB, BC, CD и DA. Диагонали в данном случае — это AC и BD.


Каковы характеристики квадрата?

1. Противоположные стороны параллельны:

На рисунке выше AB и CD параллельны, а BC и AD параллельны друг другу.В квадрате противоположные участки всегда параллельны.


2. Все стороны равны:

Все стороны квадрата равны. Например, если AB имеет длину 5 см, BC, CD и AD также будут иметь длину 5 см каждый.


3. Все углы прямые:

В квадрате углы, образованные сторонами, являются прямыми углами. На приведенном выше рисунке каждый из углов — ABC, ∠BCD, ∠CDA и ∠DAC составляет 90 градусов каждый.

4. Смежные углы являются дополнительными:

В квадратах смежные углы являются дополнительными, т.е.е., они складываются в 180 градусов. Так, на приведенном выше рисунке, например, углы BAD и ∠ADC в сумме составляют 180 градусов, поскольку они являются смежными углами.


5. Диагонали равны:

Диагонали квадрата равны друг другу. В данном случае диагонали — это BD и AC, которые в квадратах имеют одинаковую длину.

6. Диагонали перпендикулярны биссектрисам:

Диагонали BD и OC пересекаются в точке O. Для квадратов они делят друг друга пополам под углом 90 градусов, т.е.е., они перпендикулярны биссектрисам.


Вы можете спросить, в чем разница между прямоугольником и квадратом? По сути, есть два основных различия, когда мы сравниваем квадрат и прямоугольник.

В чем разница между прямоугольником и квадратом?

Основание

Квадрат

Прямоугольник

Длина

Все четыре стороны равны по длине

Все четыре стороны равны по длине

Диагонали

Диагонали делятся пополам под углом 90 градусов

Диагонали не делятся пополам под 90 градусами

Это основное различие между прямоугольником и квадратом.

Окружности, треугольники, квадраты и прямоугольники — математика для 2-го класса

Узнайте об основных фигурах

Мы видим формы везде.

Мы видим их у себя дома, в школе и даже на детской площадке.

Вы видите круги, треугольники, квадраты и прямоугольники?

Замечательно! Давайте узнаем больше об этих формах. 😎

Круг

Круг состоит из изогнутой линии, которая идет по кругу. У него без прямых сторон, и без углов.

Вот несколько примеров кругов.

Можете ли вы думать о других предметах, относящихся к кругу? 😀

Треугольник

Треугольник имеет 3 стороны, и 3 угла.

стороны — прямые линии, составляющие треугольник.

угла — это точки пересечения двух линий.

Это треугольник.

В нашем примере стороны треугольника имеют одинаковую длину.Это составляет три равных угла .

Угол — это расстояние между двумя линиями, образующими угол.

Стороны и углы треугольника не всегда должны быть равны. Прямо как треугольники ниже.

Вы узнаете больше об этих типах треугольников позже.

Квадрат

У квадрата равные стороны. Это означает, что его стороны имеют одинаковую длину. Он также имеет 4 угла , которые составляют 4 равных угла.

Это углы квадрата.

Вот примеры квадратных вещей.

Что еще вокруг вас квадратное? 😀

Прямоугольник
Прямоугольник имеет 2 короткие стороны и 2 длинные стороны . Он также имеет 4 угла , которые составляют 4 равных угла.

Это углы прямоугольника.

Давайте рассмотрим некоторые примеры прямоугольных предметов в школе.

Какие еще прямоугольные объекты вам известны? 😎

Время испытания

Все ли квадраты прямоугольники?

Да! Все квадраты являются прямоугольниками 🤓, но не все прямоугольники являются квадратами!

Смотри и учись

Отличная работа по изучению основных форм.

Теперь вы практикуете то, что вы узнали.

Рисование основных фигур | Справка SketchUp

Многие модели начинаются с основных форм.В SketchUp инструменты фигур помогают рисовать прямоугольники, круги и многоугольники. Вы найдете эти инструменты на панели инструментов «Приступая к работе», на панели инструментов «Рисование» и на панели инструментов «Большой набор инструментов».

Рисование прямоугольника или квадрата

В SketchUp прямоугольники можно рисовать практически где угодно:

  • На плоскости
  • На вертикальной плоскости
  • На существующих забоях
  • Отдельно от существующей геометрии (выровнено по плоскости осей)
  • На основе существующей геометрии

Чтобы нарисовать прямоугольник с помощью инструмента «Прямоугольник», выполните следующие действия:

  1. Выберите инструмент Прямоугольник () на панели инструментов или нажмите клавишу R .Курсор изменится на карандаш с прямоугольником.

    Совет: Чтобы начать сначала в любой момент во время этих шагов, нажмите Esc .

  2. Щелкните, чтобы установить первую угловую точку прямоугольника. .
  3. Щелкните, чтобы установить первую угловую точку прямоугольника. Чтобы выровнять плоскость вашего прямоугольника с определенной осью чертежа или другой геометрией, нажмите клавишу со стрелкой, которая соответствует желаемому выравниванию, как описано далее в этом разделе.
  4. Щелкните, чтобы установить первую угловую точку прямоугольника.Чтобы выровнять плоскость вашего прямоугольника с определенной осью чертежа или другой геометрией, нажмите клавишу со стрелкой, которая соответствует желаемому выравниванию, как описано далее в этом разделе. Если вы предпочитаете рисовать прямоугольник из центра, нажмите клавишу Ctrl (Windows) или клавишу Option (macOS).
  5. Переместите курсор по диагонали, чтобы найти нужный размер и форму прямоугольника. Чтобы нарисовать прямоугольник с точными размерами, используйте поле «Измерения», в котором при перемещении курсора отображаются размеры вашего прямоугольника.Чтобы помочь вам разместить прямоугольник относительно осей рисования или другой геометрии, механизм вывода SketchUp отображает на экране подсказки. Когда появится нужный вывод, переходите к шагу 4. Выводы в поле «Измерения» и в инструменте «Прямоугольник» объясняются немного позже в этом разделе.
  6. Щелкните еще раз, чтобы задать вторую угловую точку прямоугольника. Ваша фигура отображается с лицом, как показано на следующем рисунке.
  7. Щелкните еще раз, чтобы задать вторую угловую точку прямоугольника.Или, если вы рисуете прямоугольник из центра, щелкните еще раз, чтобы установить любую угловую точку. Ваша фигура отображается с лицом, как показано на следующем рисунке.

Когда вы рисуете прямоугольник, поле «Измерения» помогает вам моделировать в точности следующим образом:

  • Установите длину и ширину. Введите значение длины, запятую, значение ширины и нажмите Введите . Например, введите 8 ‘, 20’ и нажмите Введите . Если вы вводите только число или числа, SketchUp использует текущую настройку единиц измерения документа.Вы также можете изменить настройку единиц измерения документа, указав британские (например, 1’6 «) или метрические (например, 3,652 м ) единицы.
  • Укажите только длину или ширину. Если ввести значение и запятую ( 3 ‘, ), новое значение будет применено к первому измерению, а второе измерение не изменится. Точно так же, если вы введете запятую, а затем значение (, 3 ’), изменится только второе измерение.
  • Измените положение прямоугольника на отрицательные числа. Если вы вводите отрицательное значение ( –24, –24 ), SketchUp применяет это значение в направлении, противоположном тому, которое вы указали при рисовании.

Совет: Нет необходимости щелкать поле Измерения перед вводом значения. Во время рисования поле «Измерения» ждет, когда вы введете точные измерения, если вы захотите это сделать. Кроме того, пока вы не выберете другой инструмент или не нарисуете другой прямоугольник, вы можете использовать поле «Измерения», чтобы изменять размеры прямоугольника сколько угодно раз.

Примечание: Если вы используете неанглийскую клавиатуру, используйте запятую для обозначения десятичного разряда и точку с запятой для разделения размеров. Например, вы можете ввести две стороны прямоугольника как: 7,6 м; 4,3 м

Когда вы перемещаете курсор с выбранным инструментом «Прямоугольник», механизм вывода SketchUp отображает следующие подсказки:

Необходимо выровнять плоскость прямоугольника с осью чертежа или другой геометрией? Клавиши со стрелками могут помочь, как описано в следующей таблице.

Ключ-модификатор Фиксирует плоскость прямоугольника так, чтобы она совпадала с… Как это выглядит на экране
Стрелка влево Зеленая ось
Стрелка вверх Голубая ось
Стрелка вправо Красная ось
Стрелка вниз Предполагаемая геометрия

На видео вы можете увидеть эти функции инструмента «Прямоугольник» в действии.

Рисование повернутого прямоугольника

Инструмент «Повернутый прямоугольник» может пригодиться, когда вам нужно нарисовать прямоугольник, грань которого находится под углом к ​​красной, зеленой или синей осям SketchUp по умолчанию или к другой геометрии.

Как и инструмент «Прямоугольник», инструмент «Повернутый прямоугольник» позволяет создавать точные прямоугольники и квадраты и выводить на экран выводы, которые помогут вам при рисовании. Однако, когда вы создаете прямоугольник с помощью инструмента «Повернутый прямоугольник», вы также располагаете прямоугольник под углом.На следующем рисунке показан пример прямоугольника, созданного с помощью инструмента «Прямоугольник с поворотом».

Чтобы создать повернутый прямоугольник, выполните следующие действия:

  1. На панели инструментов в меню «Инструменты для фигур» выберите инструмент «Прямоугольник с поворотом» (). Или выберите Draw> Shapes> Rotated Rectangle в строке меню.
  2. (Необязательно) Нажмите клавишу со стрелкой, чтобы задать плоскость для повернутого прямоугольника в соответствии с таблицей, приведенной ранее в этой статье. Например, нажмите клавишу со стрелкой влево, чтобы ограничить плоскость повернутого прямоугольника зеленой плоскостью.
  3. Щелкните один раз, чтобы задать первый угол прямоугольника.
  4. Создайте первый край вашего повернутого прямоугольника. Сделать это можно двумя способами:
    • Введите точное измерение и нажмите Введите .
    • Или переместите курсор в то место, где вы хотите разместить вторую конечную точку этого ребра, используя механизм вывода SketchUp, чтобы расположить конечную точку относительно осей или другой геометрии, как показано на следующем рисунке, а затем щелкните.

      Совет: Вы можете использовать несколько клавиш-модификаторов при выполнении этого шага. Удерживайте нажатой клавишу Shift , чтобы ограничить первый край его текущим направлением. Клавиша Alt (Windows) или Command (macOS) блокирует плоскость транспортира. Или клавиши со стрелками снова могут помочь вам выровнять первый край по оси. Просто нажмите кнопку со стрелкой, соответствующую желаемому выравниванию, как объяснялось ранее в этом разделе. Например, нажмите клавишу со стрелкой вправо, чтобы ограничить первый край так, чтобы он был выровнен по красной оси.

  5. На этом этапе вы устанавливаете ширину и угол вашего прямоугольника. Вы можете установить эти значения несколькими способами:
    • Введите угол и ширину в поле «Измерения», следуя подсказке.
    • Введите ширину и угол в поле «Измерения», следуя подсказке.
    • Переместите транспортир, чтобы установить угол, и переместите курсор от центра транспортира, чтобы установить ширину, как показано на следующем рисунке.Чтобы ограничить угол, удерживайте клавишу Shift . Щелкните, чтобы завершить создание повернутого прямоугольника.

Совет: Нажмите клавишу Alt (Windows) или Command (macOS), чтобы установить базовую линию транспортира в текущем положении курсора, а затем переместите курсор, чтобы измерить угол от заданной базовой линии. Этот метод полезен, если вы хотите измерить угол от точки, отличной от базовой линии, установленной на шаге 3. Появится пунктирная линия, чтобы вы могли увидеть новую базовую линию.

Примечание: , если вы используете неанглийскую клавиатуру, вы захотите использовать запятую для обозначения десятичного разряда и точку с запятой для разделения значений в поле «Измерения». Например, вы можете ввести угол и ширину второй кромки как 43,2; 8,2 м , чтобы получить угол 43,2 градуса и длину 8,2 метра.

Примечание: , если вы используете неанглийскую клавиатуру, вы захотите использовать запятую для обозначения десятичного разряда и точку с запятой для разделения значений в поле «Измерения».Например, вы можете ввести ширину и угол второй кромки как 8,2 м; 43,2 , чтобы получить ширину 8,2 метра и угол 43,2 градуса.

Рисование круга или эллипса

Прежде чем рисовать круг, полезно понять, как SketchUp создает объекты круга:

  • Объекты окружности имеют радиус и соединяют несколько отрезков линии.
  • Эти сегменты действуют как одна линия в том смысле, что они могут определять край грани и разделять грань.Кроме того, при выборе одного сегмента выделяется весь круговой объект.
    • Механизм вывода
  • SketchUp по-прежнему видит сегменты в круге. Итак, если вы наведете указатель мыши на окружность объекта круга, вы увидите выводы конечной и средней точки.

Чтобы нарисовать круг, выполните следующие действия:

  1. На панели инструментов выберите инструмент Окружность () в раскрывающемся меню рядом с инструментом Прямоугольник. Или нажмите клавишу C . Курсор изменится на карандаш с кружком, а в поле «Измерения» будет указано количество сторон по умолчанию: 24, как показано на рисунке.Чтобы изменить количество сторон, вы можете ввести значение сейчас или подождать, пока не закончите рисовать круг.
  2. Щелкните, чтобы разместить центральную точку круга. В поле «Измерения» отображается радиус круга. Вы можете ввести значение радиуса сейчас или сразу после рисования круга.
  3. Щелкните, чтобы разместить центральную точку круга. Чтобы выровнять плоскость вашего круга с определенной осью рисования или другой геометрией, нажмите клавишу со стрелкой, которая соответствует желаемому выравниванию.Например, стрелка вверх выравнивает плоскость круга по синей оси. Подробную информацию см. В таблице в разделе Рисование прямоугольника или квадрата. В поле «Измерения» отображается радиус круга. Вы можете ввести значение радиуса сейчас или сразу после рисования круга.
  4. Переместите курсор из центральной точки, чтобы определить радиус круга. При перемещении курсора значение радиуса динамически отображается в поле «Измерения». Нажмите Esc в любой момент, чтобы начать все заново.
  5. Щелкните, чтобы закончить круг. SketchUp создает лицо в форме круга, как показано на рисунке.

  6. (Необязательно) Пока вы не выберете новый инструмент или не нарисуете новый круг, вы можете использовать поле «Измерения», чтобы изменить радиус круга или количество сторон следующим образом:
    • Чтобы изменить количество сторон: Введите число и букву S (например, введите 5s для 5 сторон или 42s для 42 сторон).Затем нажмите Введите .
    • Чтобы изменить количество сторон: Введите число и букву S (например, введите 5s для 5 сторон или 42s для 42 сторон). Затем нажмите Введите . Кроме того, вы можете удерживать клавишу Ctrl (Microsoft Windows) или клавишу Option (macOS), одновременно нажимая + или —, чтобы увеличить или уменьшить количество сторон соответственно. Если вы используете французско-канадскую клавиатуру, удерживайте клавишу Ctrl (Microsoft Windows) и клавишу + / = , чтобы увеличить сегменты.Для macOS нажмите Command и = , чтобы увеличить сегменты, или –, чтобы уменьшить сегменты.
    • Чтобы изменить радиус: Введите число и единицу измерения (при желании), например, 6 дюймов , 8 ’, 34 см или 7 м . Затем нажмите Введите или Верните . Совет: Диалоговое окно «Информация об объекте» предлагает удобный способ редактировать значения сторон и радиуса в любое время. Дополнительные сведения см. В разделе «Редактирование фигур» далее в этой статье.

Чтобы нарисовать эллипс или овал, выполните следующие действия:

  1. Нарисуйте окружность с помощью инструмента Окружность .
  2. Выберите инструмент Масштаб ().
  3. Щелкните кружок. Вокруг круга отображается ограничивающая рамка с восемью зелеными ручками.
  4. Щелкните одну из средних ручек (не одну из угловых) и переместите мышь, чтобы превратить круг в эллипс, как показано здесь.
  5. Нажмите еще раз, когда закончите масштабировать круг.

Рисование многоугольника

Вы можете создавать полигональные объекты с помощью инструмента «Многоугольник». (В этом нет ничего удивительного.) Тем не менее, вот несколько фактов, которые вы можете не знать о многоугольниках, но которые полезно знать при их рисовании:

  • В SketchUp многоугольник имеет радиус и 3 или более сторон. Таким образом, размер вашего многоугольника измеряется от центральной точки, а количество сторон определяет тип рисованного многоугольника. Пятиугольник в виде 5 сторон; восьмиугольник имеет 8 сторон.
  • Многоугольники действуют как одна линия, так как они могут определять край грани, а также разделять грань. При выборе одной стороны многоугольника выделяется весь многоугольник.
  • Механизм вывода SketchUp интерпретирует каждую сторону многоугольника как сегмент. Когда вы наводите курсор на многоугольник, вы видите конечную точку, среднюю точку и исходные точки.
  • Вы можете рисовать многоугольники на гранях или отдельно от существующей геометрии.

Чтобы нарисовать многоугольник, выполните следующие действия:

  1. Выберите инструмент Многоугольник () на панели инструментов.Курсор изменится на карандаш с многоугольником. В поле «Измерения» указано текущее количество сторон. Чтобы изменить количество сторон многоугольника, вы можете ввести числовое значение сейчас или дождаться завершения рисования.
  2. Щелкните, чтобы разместить центральную точку многоугольника. В поле «Измерения» отображается радиус. Вы можете ввести значение радиуса сейчас или сразу после рисования многоугольника.
  3. Щелкните, чтобы разместить центральную точку многоугольника. Чтобы выровнять плоскость вашего многоугольника с определенной осью рисования или другой геометрией, нажмите клавишу со стрелкой, которая соответствует желаемому выравниванию.Например, стрелка вверх выровняет плоскость многоугольника по синей оси. См. Более подробную информацию в предыдущей таблице в разделе Рисование прямоугольника или квадрата. В поле «Измерения» отображается радиус. Вы можете ввести значение радиуса сейчас или сразу после рисования многоугольника.
  4. Переместите курсор из центральной точки, чтобы определить радиус многоугольника. При перемещении курсора значение радиуса динамически отображается в поле «Измерения». Чтобы указать радиус, введите значение и нажмите Введите .Вы также можете нажать Esc , чтобы начать все заново.
  5. Щелкните второй раз, чтобы закончить многоугольник. Здесь вы видите 5-сторонний многоугольник.
  6. (Необязательно) Пока вы не выберете новый инструмент или не нарисуете новый многоугольник, вы можете использовать поле Измерения, чтобы изменить радиус или количество сторон следующим образом:
    • Чтобы изменить количество сторон: Введите число и букву S (например, введите 5s для 5 сторон или 42s для 42 сторон).Затем нажмите Введите .
    • Чтобы изменить количество сторон: Введите число и букву S (например, введите 5s для 5 сторон или 42s для 42 сторон). Затем нажмите Введите . Кроме того, вы можете удерживать клавишу Ctrl (Microsoft Windows) или клавишу Option (macOS), одновременно нажимая + или —, чтобы увеличить или уменьшить количество сторон соответственно. Если вы используете французско-канадскую клавиатуру, удерживайте клавишу Ctrl (Microsoft Windows) и клавишу + / = , чтобы увеличить сегменты.Для macOS нажмите Command и = , чтобы увеличить сегменты, или –, чтобы уменьшить сегменты.
    • Чтобы изменить радиус: Введите число и единицу измерения (при желании), например, 6 дюймов , 8 ’, 34 см или 7 м . Затем нажмите Введите или Верните .

    Совет: Хотя инструмент «Многоугольник» работает аналогично инструменту «Круг», разница между инструментами становится очевидной, когда вы нажимаете / вытягиваете круг или многоугольник в трехмерную форму.Края круга выглядят гладкими, но края многоугольника имеют четкие стороны, как показано здесь.


В этом видеоролике вы можете увидеть, как инструменты «Круг» и «Многоугольник» демонстрируют все свои трюки.

Редактирование форм

Диалоговое окно «Информация об объекте» позволяет изменить радиус или стороны круга или многоугольника в любое время после создания формы. Вот как:

  1. Щелкните правой кнопкой мыши край (не грань) круга или многоугольника, который вы хотите отредактировать.
  2. Выберите Entity Info из появившегося контекстного меню, как показано здесь.
  3. На панели «Информация об объекте» щелкните поле Radius или Segments , измените значение и нажмите Введите (Microsoft Windows) или Return (Mac). После того, как вы нажмете Enter или Return, ваша форма немедленно отобразит ваши изменения.

SketchUp не позволяет изменять ширину или длину прямоугольника в любое время.Если вы уже выбрали другой инструмент или нарисовали дополнительные прямоугольники, вам нужно стереть прямоугольник, который вы хотите изменить, и перерисовать его. Подробнее см. Рисование прямоугольника. Или измените размер прямоугольника с помощью инструмента «Масштаб», если вам не нужно вводить точные размеры.

Конечно, вы можете сделать гораздо больше, чем просто изменить размер фигуры. Вы можете превратить 2D-форму в 3D-форму с помощью инструмента Push / Pull.

Обновлено: 01.08.2021 — 17:04

Добавить комментарий

Ваш адрес email не будет опубликован. Обязательные поля помечены *